Ball Mill (Perfect Mixing): Difference between revisions
Scott Munro (talk | contribs) m (1 revision imported) |
imported>Scott.Munro m (→See also) |
||
| (17 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
This article describes an implementation of the '''Perfect Mixing''' ball mill model outlined by Napier-Munn et al. (1996).{{Napier-Munn_et_al._(1996)}} | This article describes an implementation of the '''Perfect Mixing''' ball mill model outlined by Napier-Munn et al. (1996).{{Napier-Munn_et_al._(1996)}} | ||
The model described here is for '''''steady-state''''' simulation. For dynamic simulation, '' | The model described here is for '''''steady-state''''' simulation. For dynamic simulation, see ''[[Ball Mill (Perfect Mixing, Dynamic)]]''. | ||
== Model theory == | == Model theory == | ||
{{Restricted content}} | |||
<hide> | |||
{{Model theory (Text, Mill, Perfect Mixing, Population Balance)}} | |||
</hide><div class="user-show"> | |||
=== Discharge rate === | === Discharge rate === | ||
</div><hide> | |||
[[File:TumblingMillDimensions2.png|thumb|500px|Figure 2. Schematic of a tumbling mill showing key dimensions.]] | [[File:TumblingMillDimensions2.png|thumb|500px|Figure 2. Schematic of a tumbling mill showing key dimensions.]] | ||
| Line 59: | Line 33: | ||
with <math>R_i/D_i</math> becoming <math>R_i/D_i^*</math> for mill model calibration and simulation. | with <math>R_i/D_i</math> becoming <math>R_i/D_i^*</math> for mill model calibration and simulation. | ||
</hide><div class="user-show"> | |||
=== Breakage rate === | === Breakage rate === | ||
</div><hide> | |||
The <math>R_i/D_i^*</math> rate is a function of particle size and is typically a smooth, concave downward curve with a maximum related to ball size. In order to reduce the number of model parameters, the rates are specified only at three or four regularly spaced sizes (''knots''). Cubic spline interpolation is then used to reconstruct the complete set of rates for all size intervals. | The <math>R_i/D_i^*</math> rate is a function of particle size and is typically a smooth, concave downward curve with a maximum related to ball size. In order to reduce the number of model parameters, the rates are specified only at three or four regularly spaced sizes (''knots''). Cubic spline interpolation is then used to reconstruct the complete set of rates for all size intervals. | ||
| Line 65: | Line 41: | ||
The breakage rate, <math>R_i</math>, is affected by mill operating conditions and the <math>R_i/D_i^*</math> rate is further scaled by the following relation: | The breakage rate, <math>R_i</math>, is affected by mill operating conditions and the <math>R_i/D_i^*</math> rate is further scaled by the following relation: | ||
:<math>\left(\frac{R}{D^*}\right)_{Sim} = \left(\frac{R}{D^*}\right)_{ | :<math>\left(\frac{R}{D^*}\right)_{\rm Sim} = \left(\frac{R}{D^*}\right)_{\rm Orig} \cdot f_{\rm D} \cdot f_{\rm LF} \cdot f_{\rm CS} \cdot f_{\rm WI} \cdot f_{\rm Db}</math> | ||
{{Model theory (Text, Ball Mill, Perfect Mixing, Breakage Scaling)}} | |||
The grouping of breakage rate scaling factors above, excluding work index, essentially represents a relationship with mill power draw, as noted by Napier-Munn et al., King and others.{{Napier-Munn_et_al. (1996)}}{{King (2012)}} | |||
The grouping of breakage rate scaling factors above, excluding work index, essentially | |||
</hide><div class="user-show"> | |||
=== Appearance function === | === Appearance function === | ||
</div><hide> | |||
{{Model theory (Text, Ball Mill, Perfect Mixing, Appearance)}} | |||
</hide><div class="user-show"> | |||
=== Internal mesh series === | === Internal mesh series === | ||
</div><hide> | |||
{{Model theory (Text, Ball Mill, Perfect Mixing, Internal mesh)|Perfect Mixing}} | |||
</hide><div class="user-show"> | |||
=== Multi-component modelling === | === Multi-component modelling === | ||
</div><hide> | |||
{{Model theory (Text, Ball Mill, Perfect Mixing, Multi-component)|Perfect Mixing|breakage rates, and breakage rate}} | |||
</hide><div class="user-show"> | |||
=== Power draw === | === Power draw === | ||
</div><hide> | |||
The Perfect Mixing mill model formulation does not explicitly include a relationship with mill power draw, other than the breakage rate scaling observations noted above. | The Perfect Mixing mill model formulation does not explicitly include a relationship with mill power draw, other than the breakage rate scaling observations noted above. | ||
However, a simple estimate of power draw is provided for user convenience. Power is calculated according to the [[Tumbling Mill (Power, Morrell Empirical)|Morrell Empirical]] approach for grate and overflow discharge mills.{{Morrell_(1996b)}} | However, a simple estimate of power draw is provided for user convenience. Power is calculated according to the [[Tumbling Mill (Power, Morrell Empirical)|Morrell Empirical]] approach for grate and overflow discharge mills.{{Morrell_(1996b)}} | ||
</hide> | |||
== Excel == | == Excel == | ||
| Line 141: | Line 88: | ||
:<math>Parameters= | :<math>Parameters= | ||
\begin{bmatrix} | \begin{bmatrix} | ||
D_{Orig}\text{ (m)}\\ | D_{\rm Orig}\text{ (m)}\\ | ||
{\rm LF}_{\rm Orig}\text{ (v/v)}\\ | |||
(C_{\rm s})_{\rm Orig}\text{ (frac)}\\ | |||
{\rm WI}_{\rm Orig}\text{ (kWh/t)}\\ | |||
Db_{Orig}\text{ (mm)}\\ | Db_{\rm Orig}\text{ (mm)}\\ | ||
D_{Sim}\text{ (m)}\\ | D_{\rm Sim}\text{ (m)}\\ | ||
{\rm LF}_{\rm Sim}\text{ (v/v)}\\ | |||
(C_{\rm s})_{\rm Sim}\text{ (frac)}\\ | |||
{\rm WI}_{\rm Orig}\text{ (kWh/t)}\\ | |||
Db_{Sim}\text{ (mm)}\\ | Db_{\rm Sim}\text{ (mm)}\\ | ||
K\\ | K\\ | ||
L\text{ (m)}\\ | L\text{ (m)}\\ | ||
\alpha_{c}\text{ (deg.)}\\ | \alpha_{c}\text{ (deg.)}\\ | ||
D_{\rm t}\text{ (m)}\\ | |||
J_{\rm B}\text{ (v/v)}\\ | |||
U\text{ (v/v)}\\ | U\text{ (v/v)}\\ | ||
\ | \rho_{\rm B}\text{ (t/m}^{\text{3}}\text{)}\\ | ||
(Q_{M,F})_{ | (Q_{\rm M,F})_{\rm L}\text{ (t/h)}\\ | ||
\ | \rho_{\rm L}\text{ (t/m}^{\text{3}}\text{)}\\ | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
| Line 169: | Line 116: | ||
MillFeed= \begin{bmatrix} | MillFeed= \begin{bmatrix} | ||
(Q_{M,F})_{11}\text{ (t/h)} & \dots & (Q_{M,F})_{1m}\text{ (t/h)}\\ | (Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\ | ||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
(Q_{M,F})_{n1}\text{ (t/h)} & \dots & (Q_{M,F})_{nm}\text{ (t/h)}\\ | (Q_{\rm M,F})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{nm}\text{ (t/h)}\\ | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
OreSG= \begin{bmatrix} | OreSG= \begin{bmatrix} | ||
(\rho_{\rm S})_{1}\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_{\rm S})_m\text{ (t/m}^\text{3}\text{)}\\ | |||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| Line 194: | Line 141: | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
{\rm WI}_{\rm Sim}= \begin{bmatrix} | |||
{\rm WI}_{1}\text{ (kWh/t)} & \dots & {\rm WI}_m\text{ (kWh/t)}\\ | |||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
| Line 208: | Line 155: | ||
\vdots\\ | \vdots\\ | ||
\ln\left(\frac{R}{D^*}\right)_k\\ | \ln\left(\frac{R}{D^*}\right)_k\\ | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
where: | where: | ||
* <math>\alpha_{c}</math> is angle between the cone end surface and the vertical direction (degrees) | * <math>\alpha_{c}</math> is angle between the cone end surface and the vertical direction (degrees) | ||
* <math> | * <math>D_{\rm t}</math> is the diameter of the discharge trunnion (m) | ||
* <math> | * <math>J_{\rm B}</math> is the ball charge volume fraction (typically <math>J_{\rm B} = {\rm LF}</math> for ball mills) (v/v) | ||
* <math>U</math> is the void fill fraction, the volumetric fraction of grinding media interstitial void space occupied by slurry (v/v) | * <math>U</math> is the void fill fraction, the volumetric fraction of grinding media interstitial void space occupied by slurry (v/v) | ||
* <math>\ | * <math>\rho_{\rm B}</math> is the Specific Gravity or density of the ball media (excluding void space) (- or t/m<sup>3</sup>) | ||
* <math>(Q_{M,F})_{ | * <math>(Q_{\rm M,F})_{\rm L}</math> is the mass flow feed rate of liquids into the mill (t/h) | ||
* <math>\ | * <math>\rho_{\rm L}</math> is the Specific Gravity or density of liquids in the feed (- or t/m<sup>3</sup>) | ||
* <math>n</math> is the number of size intervals | * <math>n</math> is the number of size intervals | ||
* <math>m</math> is the number of ore types | * <math>m</math> is the number of ore types | ||
| Line 224: | Line 171: | ||
* <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm) | * <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm) | ||
* <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm) | * <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm) | ||
* <math>Q_{M,F}</math> is the mass flow rate of particles in the feed (t/h) | * <math>Q_{\rm M,F}</math> is the mass flow rate of particles in the feed (t/h) | ||
* <math> | * <math>\rho_{\rm S}</math> is the Specific Gravity or density of solids (- or t/m<sup>3</sup>) | ||
* <math>A_i</math> is the Appearance function value, the fraction of parent particle mass appearing in internal size interval <math>i</math> (frac) | * <math>A_i</math> is the Appearance function value, the fraction of parent particle mass appearing in internal size interval <math>i</math> (frac) | ||
* <math>\frac{R_i}{D_i^*}</math> is breakage rate per discharge rate normalised for residence time (h<sup>-1</sup>/h<sup>-1</sup>/h) | * <math>\frac{R_i}{D_i^*}</math> is breakage rate per discharge rate normalised for residence time (h<sup>-1</sup>/h<sup>-1</sup>/h) | ||
<!-- | |||
\quad \text{ or } \quad | |||
\begin{bmatrix} | |||
\ln\left(\frac{R}{D^*}\right)_{11} & \dots & \ln\left(\frac{R}{D^*}\right)_{1m}\\ | |||
\vdots & \ddots & \vdots\\ | |||
\ln\left(\frac{R}{D^*}\right)_{k1} & \dots & \ln\left(\frac{R}{D^*}\right)_{km}\\ | |||
\end{bmatrix} | |||
--> | |||
=== Results === | === Results === | ||
| Line 238: | Line 193: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
\text{ | Q_{\rm V,F}\text{ (m}^{\text{3}}\text{/h)}\\ | ||
\text{ | V\text{ (m}^{\text{3}}\text{)}\\ | ||
\text{ | \text{N (rpm)}\\ | ||
\text{ | \rho_{\rm c}\text{ (t/m}^{\text{3}}\text{)}\\ | ||
\text{No-load power ( | \text{No-load power (kW)}\\ | ||
\text{Gross power (grate) (kW)}\\ | \text{Gross power (grate) (kW)}\\ | ||
\text{Gross power (overflow) (kW)}\\ | \text{Gross power (overflow) (kW)}\\ | ||
\text{R/D* factor ( | \text{R/D* factor (-)}\\ | ||
f_{\rm D}\text{ (-)}\\ | |||
f_{\rm LF}\text{ (-)}\\ | |||
f_{\rm CS}\text{ (-)}\\ | |||
x_{\rm m(small)}\text{ (mm)}\\ | |||
x_{\rm m(large)}\text{ (mm)}\\ | |||
\end{bmatrix} | \end{bmatrix} | ||
| Line 266: | Line 221: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
(Q_{M,P})_{11}\text{ (t/h)} & \dots & (Q_{M,P})_{1m}\text{ (t/h)}\\ | (Q_{\rm M,P})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,P})_{1m}\text{ (t/h)}\\ | ||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
(Q_{M,P})_{n1}\text{ (t/h)} & \dots & (Q_{M,P})_{nm}\text{ (t/h)}\\ | (Q_{\rm M,P})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,P})_{nm}\text{ (t/h)}\\ | ||
\end{bmatrix} | \end{bmatrix} | ||
| Line 316: | Line 271: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
( | (f_{\rm WI})_1 & \dots & (f_{\rm WI})_m | ||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
| Line 328: | Line 283: | ||
where: | where: | ||
* <math>\ | * <math>Q_{\rm V,F}</math> is the flow rate of pulp into the mill (m<sup>3</sup>/h) | ||
* <math> | * <math>V</math> is the total volume inside the mill, calculated as the sum of a cylinder and two frustums (m<sup>3</sup>) | ||
* <math> | * <math>N</math> is the [[Tumbling Mill (Speed)|rotational rate of the mill]] (rpm) | ||
* <math>\ | * <math>\rho_{\rm c}</math> is the combined density of the charge, including grinding media, coarse ore, slurry and void space (t/m<sup>3</sup>) | ||
* <math>\text{No-load power}</math> is the power input to the motor when the mill is rotating but empty (no balls, rocks or slurry) (kW) | * <math>\text{No-load power}</math> is the power input to the motor when the mill is rotating but empty (no balls, rocks or slurry) (kW) | ||
* <math>\text{Gross power (grate)}</math> is the total power input to the motor if the mill is configured with a grate discharge (kW) | * <math>\text{Gross power (grate)}</math> is the total power input to the motor if the mill is configured with a grate discharge (kW) | ||
* <math>\text{Gross power (overflow)}</math> is the total power input to the motor if the mill is configured with an overflow discharge (kW) | * <math>\text{Gross power (overflow)}</math> is the total power input to the motor if the mill is configured with an overflow discharge (kW) | ||
* <math>\text{R/D* factor}=D_i^*/D_i</math> is the discharge rate scaling factor | * <math>\text{R/D* factor}=D_i^*/D_i</math> is the discharge rate scaling factor | ||
* <math>Q_{M,P}</math> is the mass flow rate of particles in the mill product (t/h) | * <math>Q_{\rm M,P}</math> is the mass flow rate of particles in the mill product (t/h) | ||
* <math>\bar{d}_i</math> is the [[Conversions|geometric mean size]] of the internal mesh series interval that mass is retained on (mm) | * <math>\bar{d}_i</math> is the [[Conversions|geometric mean size]] of the internal mesh series interval that mass is retained on (mm) | ||
| Line 353: | Line 308: | ||
== SysCAD == | == SysCAD == | ||
The SysCAD interface | The sections and variable names used in the SysCAD interface are described in detail in the following tables. | ||
{{SysCAD (Page, | {{SysCAD (Page, Mill, DLL*Mill)|PowerModels=true|MediaTraj=true|MediaStrings=true|Overfilling=true}} | ||
{{SysCAD (Page, Ball Mill, Perfect Mixing, Mill)|method=0}} | {{SysCAD (Page, Ball Mill, Perfect Mixing, Mill)|method=0}} | ||
{{SysCAD (Page, Ball Mill, Perfect Mixing, Ore)}} | {{SysCAD (Page, Ball Mill, Perfect Mixing, Ore)|method=Ball}} | ||
{{SysCAD (Page, Ball Mill, Perfect Mixing, Ri/Di)|method=0}} | {{SysCAD (Page, Ball Mill, Perfect Mixing, Ri/Di)|method=0}} | ||
{{SysCAD (Page, Tumbling Mill, Power)|modelpage= | {{SysCAD (Page, Tumbling Mill, Power)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill|HF=true|MorrellC=true|MorrellE=true|MorrellD=true|HildenPowell=true}} | ||
{{SysCAD (Page, Tumbling Mill, MediaStrings)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill}} | |||
{{SysCAD (Page, Tumbling Mill, MediaTraj)|modelpage= | {{SysCAD (Page, Tumbling Mill, MediaTraj)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill}} | ||
{{SysCAD (Page, | {{SysCAD (Page, Ball Mill, Overfilling)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill}} | ||
{{SysCAD (Page, About)}} | {{SysCAD (Page, About)}} | ||
| Line 375: | Line 332: | ||
* [[Ball Mill (Perfect Mixing, Dynamic)|Dynamic Perfect Mixing ball mill model]] | * [[Ball Mill (Perfect Mixing, Dynamic)|Dynamic Perfect Mixing ball mill model]] | ||
* [[Mill (Herbst-Fuerstenau)| Herbst-Fuerstenau mill model]] | * [[Mill (Herbst-Fuerstenau)| Herbst-Fuerstenau mill model]] | ||
== External links == | |||
* [https://help.syscad.net/Met_Dynamics_-_Mill Met Dynamics - Mill (help.syscad.net)] | |||
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Crushing_and_Grinding_Example Crushing and Grinding Example project (help.syscad.net)] | |||
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Crushing,_Grinding_and_Flotation_Example Crushing, Grinding and Flotation Example project (help.syscad.net)] | |||
== References == | == References == | ||
Latest revision as of 13:28, 1 May 2025
Description
This article describes an implementation of the Perfect Mixing ball mill model outlined by Napier-Munn et al. (1996).[1]
The model described here is for steady-state simulation. For dynamic simulation, see Ball Mill (Perfect Mixing, Dynamic).
Model theory
Discharge rate
Breakage rate
Appearance function
Internal mesh series
Multi-component modelling
Power draw
Excel
The Perfect Mixing ball mill model may be invoked from the Excel formula bar with the following function call:
=mdUnit_BallMill_PerfectMixing(Parameters as Range, Size as Range, MillFeed as Range, OreSG As Range, Appearance as Range, WorkIndexSim As Range, R/D*KnotPositions as Range, R/D*KnotsOrig as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
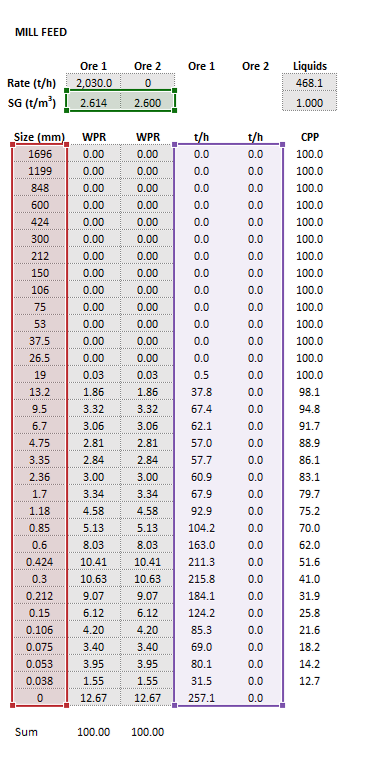
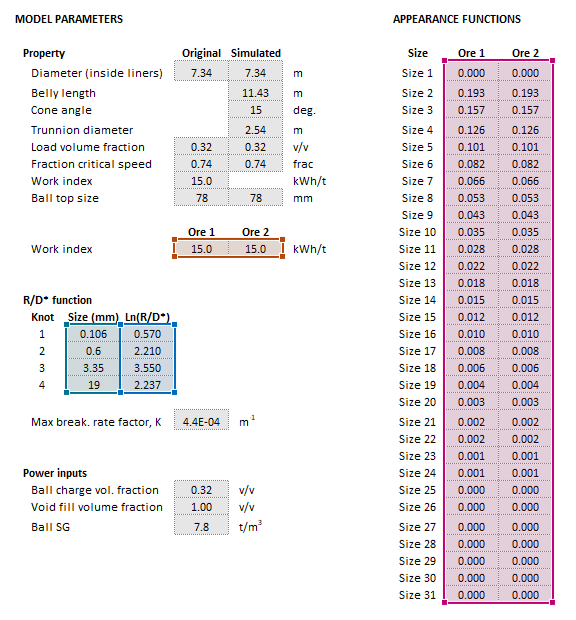
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:
where:
- is angle between the cone end surface and the vertical direction (degrees)
- is the diameter of the discharge trunnion (m)
- is the ball charge volume fraction (typically for ball mills) (v/v)
- is the void fill fraction, the volumetric fraction of grinding media interstitial void space occupied by slurry (v/v)
- is the Specific Gravity or density of the ball media (excluding void space) (- or t/m3)
- is the mass flow feed rate of liquids into the mill (t/h)
- is the Specific Gravity or density of liquids in the feed (- or t/m3)
- is the number of size intervals
- is the number of ore types
- is the number of breakage rate per discharge rate knots
- is the size of the square mesh interval that feed mass is retained on (mm)
- , i.e. descending size order from top size () to sub mesh ( mm)
- is the mass flow rate of particles in the feed (t/h)
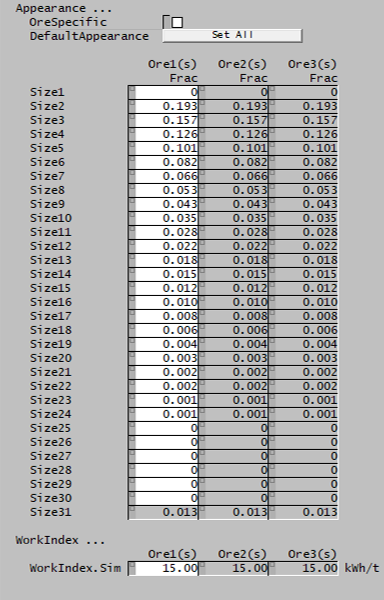
- is the Specific Gravity or density of solids (- or t/m3)
- is the Appearance function value, the fraction of parent particle mass appearing in internal size interval (frac)
- is breakage rate per discharge rate normalised for residence time (h-1/h-1/h)
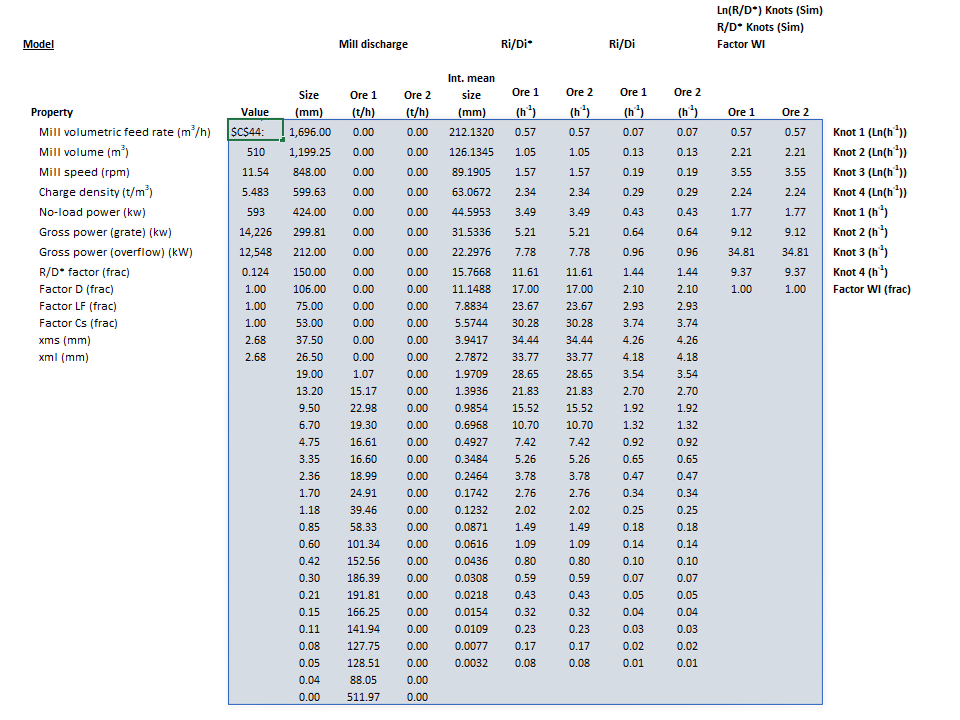
Results
The results are displayed in Excel as an array corresponding to the matrix notation below:
where:
- is the flow rate of pulp into the mill (m3/h)
- is the total volume inside the mill, calculated as the sum of a cylinder and two frustums (m3)
- is the rotational rate of the mill (rpm)
- is the combined density of the charge, including grinding media, coarse ore, slurry and void space (t/m3)
- is the power input to the motor when the mill is rotating but empty (no balls, rocks or slurry) (kW)
- is the total power input to the motor if the mill is configured with a grate discharge (kW)
- is the total power input to the motor if the mill is configured with an overflow discharge (kW)
- is the discharge rate scaling factor
- is the mass flow rate of particles in the mill product (t/h)
- is the geometric mean size of the internal mesh series interval that mass is retained on (mm)
Example
The images below show the selection of input arrays and output results in the Excel interface.
SysCAD
The sections and variable names used in the SysCAD interface are described in detail in the following tables.
MD_Mill page
The first tab page in the access window will have this name.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Tag | Display | This name tag may be modified with the change tag option. |
| Condition | Display | OK if no errors/warnings, otherwise lists errors/warnings. |
| ConditionCount | Display | The current number of errors/warnings. If condition is OK, returns 0. |
| GeneralDescription / GenDesc | Display | This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.
If this field is blank, then SysCAD will display the unit class ID. |
| Requirements | ||
| On | CheckBox | This enables the unit. If this box is not checked, then the material will pass straight through the mill with no change to the size distribution. |
| NumParallelUnits | Input | The number of parallel, identical units to simulate:
|
| Method | Fixed Discharge | The discharge particle size distribution is user defined. Different distributions can be used for different solids. |
| AG/SAG (Variable Rates) | The Variable Rates AG/SAG mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Rod Mill (Lynch) | The Lynch rod mill model is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Ball (Perfect Mixing) | The Perfect Mixing ball mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Stirred (Perfect Mixing) | The Perfect Mixing stirred mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Mill (Herbst-Fuerstenau) | The Herbst-Fuerstenau model is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| PowerModels | CheckBox | Show alternative mill power model calculations on the Power page. |
| MediaTrajectory | CheckBox | Show mill media rolling, sliding and free flight trajectory computations on the MediaTraj page. |
| OverfillingIndicator | CheckBox | Show overflow ball mill slurry volume, residence time, and overfilling evaluation on Overfilling page. |
| MediaStrings | CheckBox | Show media size distributions at recharge equilibrium on the MediaStrings page. |
| Options | ||
| ShowQFeed | CheckBox | QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream. |
| ShowQProd | CheckBox | QProd and associated tab pages (eg Sp) will become visible, showing the properties of the products. |
| SizeForPassingFracCalc | Input | Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section. |
| FracForPassingSizeCalc | Input | Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section. |
| Stream Summary | ||
| MassFlow / Qm | Display | The total mass flow in each stream. |
| SolidMassFlow / SQm | Display | The Solids mass flow in each stream. |
| LiquidMassFlow / LQm | Display | The Liquid mass flow in each stream. |
| VolFlow / Qv | Display | The total Volume flow in each stream. |
| Temperature / T | Display | The Temperature of each stream. |
| Density / Rho | Display | The Density of each stream. |
| SolidFrac / Sf | Display | The Solid Fraction in each stream. |
| LiquidFrac / Lf | Display | The Liquid Fraction in each stream. |
| Passing | Display | The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream. |
| Passes | Display | The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction. |
Mill page
The Mill page is used to specify the input parameters for the mill model.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| PerfectMixing | ||
| HelpLink | Opens a link to this page using the system default web browser. Note: Internet access is required. | |
| Ball | ||
| MediaStringsP50 | CheckBox |
|
| Diameter | Input | The inside liner diameter of the original and simulated ball mills. |
| BellyLength | Input | The inside liner belly length of the simulated ball mill, excluding cones. |
| ConeAngle | Input | Angle of the feed and discharge end cones, measured as positive displacement from the vertical direction. |
| TrunnionDiameter | Input | The inside liner trunnion diameter of the simulated ball mill. |
| LoadFrac | Input | The volumetric load fraction of the original and simulated ball mills. |
| FracCS | Input | The fraction critical speed of the original and simulated ball mills. |
| WorkIndex | Input | Bond Ball Work Index of ore in the original mill. |
| BallSize | Input | Characteristic diameter of balls in original and simulated ball mills. |
| MaxBreakageRateFactor / K | Input | Parameter relating ball size and the size at which the breakage rate per discharge rate is maximum. |
| R/DFunction | ||
| NumSplineKnots | Input | Number of spline knots for the function. |
| Size | Input | Spline knot size positions. |
| Ln(R/D*) | Input | Values of at each spline knot position. |
| Power | ||
| BallVolume | Input | Volumetric fraction of mill occupied by balls and voids. |
| VoidFillFraction | Input | Volumetric fraction of void space between balls occupied by slurry. |
| BallSG | Input | Specific Gravity or density of ball media. |
| Results | ||
| MillVolume | Display | Volume inside mill, including cones. |
| MillSpeed | Display | Rotational speed of simulated mill. |
| ChargeDensity | Display | Density of charge in simulated mill, including balls, solids and liquids. |
| NoLoadPower | Display | Power draw of empty mill (no balls, solids or liquids) |
| GrossPower.Grate | Display | Gross power draw of mill in grate configuration |
| GrossPower.Overflow | Display | Gross power draw of mill in overflow configuration |
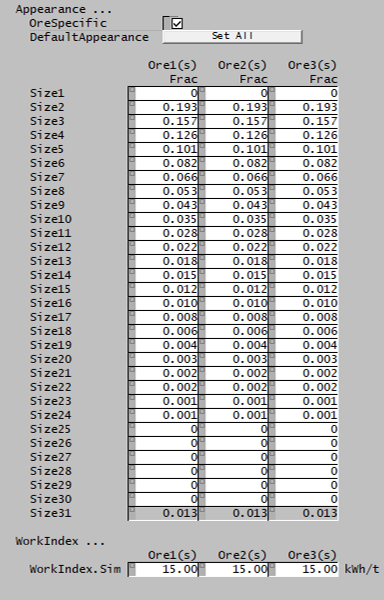
Ore page
This page is used to define the comminution properties of SysCAD species with the size distribution quality in the project.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Appearance | ||
| DefaultAppearance | Sets all species to the default Broadbent-Callcott Appearance function. | |
| OreSpecific | CheckBox |
|
| Appearance | Input | User-specified Appearance function data for all species with size distribution property. |
| WorkIndex | ||
| WorkIndex.Sim | Input | Bond Ball Work Index data for all species with size distribution property. |
Ri/Di page
This page displays the scaling factors and breakage rate per discharge rate for each size interval computed by the Perfect Mixing model.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Scaling | ||
| RDStar/RD | Display | Value of the factor for discharge rate scaling. |
| Diameter | Display | Value of the mill diameter factor for rate scaling. |
| LoadFraction | Display | Value of the load fraction factor for rate scaling. |
| FracCS | Display | Value of the fraction critical speed factor for rate scaling. |
| WorkIndex | Display | Value of the Work Index factor of each ore species for rate scaling. |
| Ri/DiStar | ||
| Size | Display | Size of each interval in internal mesh series. |
| MeanSize | Display | Geometric mean size of each interval in internal mesh series. |
| Ri/DiStar | Display | Value of normalised rate for each size interval, for each ore species. |
| Ri/Di | ||
| Size | Display | Size of each interval in internal mesh series. |
| MeanSize | Display | Geometric mean size of each interval in internal mesh series. |
| Ri/Di | Display | Value of rate for each size interval, for each ore species. |
Power page
This optional page displays the inputs and results for alternative mill power models. The page is only visible if PowerModels is selected on the MD_Mill page.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Power | ||
| HoggFuerstenau | CheckBox | Shows inputs and results for tumbling mill power calculations using the Hogg and Fuerstenau method. |
| MorrellC | CheckBox | Shows inputs and results for tumbling mill power calculations using the Morrell Continuum method. |
| MorrellE | CheckBox | Shows inputs and results for tumbling mill power calculations using the Morrell Empirical method. |
| MorrellD | CheckBox | Shows inputs and results for tumbling mill power calculations using the Morrell Discrete Shell method. |
| HildenPowell | CheckBox | Shows inputs and results for tumbling mill power calculations using the Hilden and Powell method. |
MediaStrings page
This page displays the inputs and results for grinding mill media string calculations. The page is only visible if MediaStrings is selected on the MD_Mill page.
MediaTraj page
This page displays the inputs and results for tumbling mill media trajectory calculations. The page is only visible if MediaTrajectory is selected on the MD_Mill page.
Overfilling page
This page displays the inputs and results for overflow discharge mill overfilling calculations. The page is only visible if OverfillingIndicator is selected on the MD_Mill page.
About page
This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| About | ||
| HelpLink | Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required. | |
| Information | Copies Product and License information to the Windows clipboard. | |
| Product | ||
| Name | Display | Met Dynamics software product name |
| Version | Display | Met Dynamics software product version number. |
| BuildDate | Display | Build date and time of the Met Dynamics Models SysCAD Add-On. |
| License | ||
| File | This is used to locate a Met Dynamics software license file. | |
| Location | Display | Type of Met Dynamics software license or file name and path of license file. |
| SiteCode | Display | Unique machine identifier for license authorisation. |
| ReqdAuth | Display | Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime. |
| Status | Display | License status, LICENSE_OK indicates a valid license, other messages report licensing errors. |
| IssuedTo | Display | Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to. |
| ExpiryDate | Display | Only visible if Met Dynamics license file is used. License expiry date. |
| DaysLeft | Display | Only visible if Met Dynamics license file is used. Days left before the license expires. |
See also
External links
- Met Dynamics - Mill (help.syscad.net)
- Crushing and Grinding Example project (help.syscad.net)
- Crushing, Grinding and Flotation Example project (help.syscad.net)
References
- ↑ Napier-Munn, T.J., Morrell, S., Morrison, R.D. and Kojovic, T., 1996. Mineral comminution circuits: their operation and optimisation. Julius Kruttschnitt Mineral Research Centre, Indooroopilly, QLD.