Tumbling Mill (Media Strings)

Description

The article outlines a methodology for estimating the size distribution of media elements in grinding mills at recharge equilibrium, as proposed by Sepúlveda (2004):

• The constant recharging, wearing and ejection of media elements in a mill results in a string of worn media elements of distributed sizes which descended from an original unworn (make-up) element.
• Charging a mill with a mixture of new media make-up sizes results in multiple strings coexisting, and combining into an effective overall string.
• When the addition rate of new media elements matches the ejection rate of scrap elements, the media strings are said to be in recharge equilibrium.

Sepúlveda mathematically derives an approach to estimating the mass weight by size distribution of both individual and overall combined strings at recharge equilibrium.

This information may be useful for understanding the effect of changing recharge media sizes or proportions on the overall distribution of media in a mill. It may also be useful for simulation purposes, where either full media size distributions or characteristic sizes are input parameters (e.g. AG/SAG, Perfect Mixing ball mill).

Model theory

This content is available to registered users. Please log in to view.

Excel

The grinding mill media strings model may be invoked from the Excel formula bar with the following function call:

=mdMillMediaStrings(Size as Range, TopSize as Range, RechargePolicy as Range, scrapSize as Double)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The input arrays and model results are defined below in matrix notation, along with example images showing the selection of the same arrays in the Excel interface:

${\begin{array}{l}Size={\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{n}{\text{ (mm)}}\\\end{bmatrix}},&&&{\begin{array}{lll}TopSize={\begin{bmatrix}{(d^{\rm {R}}})_{1}{\text{ (mm)}}&\dots &{(d^{\rm {R}}})_{m}{\text{ (mm)}}\\\end{bmatrix}},&&&RechargePolicy={\begin{bmatrix}r_{1}{\text{ (w/w)}}&\dots &r_{\rm {m}}{\text{ (w/w)}}\\\end{bmatrix}}&&&scrapSize=\left[d^{\rm {S}}\right]\end{array}}\end{array}}$ $mdMillMediaStrings={\begin{bmatrix}{\begin{bmatrix}-\end{bmatrix}}&{\begin{bmatrix}v_{1}{\text{ (v/v)}}&\dots &v_{m}{\text{ (v/v)}}\\\end{bmatrix}}&{\begin{bmatrix}-\end{bmatrix}}&{\begin{bmatrix}-\end{bmatrix}}&{\begin{bmatrix}-\end{bmatrix}}\\{\begin{bmatrix}-\end{bmatrix}}&{\begin{bmatrix}a_{1}{\text{ (m}}^{2}{\text{/m}}^{3}{\text{)}}&\dots &a_{m}{\text{ (m}}^{2}{\text{/m}}^{3}{\text{)}}\\\end{bmatrix}}&{\begin{bmatrix}a_{\rm {All}}{\text{ (m}}^{2}{\text{/m}}^{3}{\text{)}}\end{bmatrix}}&{\begin{bmatrix}-\end{bmatrix}}&{\begin{bmatrix}-\end{bmatrix}}\\{\begin{bmatrix}-\end{bmatrix}}&{\begin{bmatrix}(P_{50})_{1}{\text{ (mm)}}&\dots &(P_{50})_{m}{\text{ (mm)}}\\\end{bmatrix}}&{\begin{bmatrix}(P_{50})_{\rm {All}}{\text{ (mm)}}\end{bmatrix}}&{\begin{bmatrix}-\end{bmatrix}}&{\begin{bmatrix}-\end{bmatrix}}\\{\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{n}{\text{ (mm)}}\\\end{bmatrix}}&{\begin{bmatrix}F_{3}(d_{1})_{1}{\text{ (CFP)}}&\dots &F_{3}(d_{1})_{m}{\text{ (CFP)}}\\\vdots &\ddots &\vdots \\F_{3}(d_{n})_{1}{\text{ (CFP)}}&\dots &F_{3}(d_{n})_{m}{\text{ (CFP)}}\\\end{bmatrix}}&{\begin{bmatrix}F_{3}(d_{1})_{\rm {All}}{\text{ (CFP)}}\\\vdots \\F_{3}(d_{n})_{\rm {All}}{\text{ (CFP)}}\\\end{bmatrix}}&{\begin{bmatrix}f_{3}(d_{1})_{1}{\text{ (WFR)}}&\dots &f_{3}(d_{1})_{m}{\text{ (WFR)}}\\\vdots &\ddots &\vdots \\f_{3}(d_{n})_{1}{\text{ (WFR)}}&\dots &f_{3}(d_{n})_{m}{\text{ (WFR)}}\\\end{bmatrix}}&{\begin{bmatrix}f_{3}(d_{1})_{\rm {All}}{\text{ (WFR)}}\\\vdots \\f_{3}(d_{n})_{\rm {All}}{\text{ (WFR)}}\\\end{bmatrix}}\end{bmatrix}}\;\;\;\;\;\;$ where $P_{50}$ is the median size, the 50% passing size (mm).

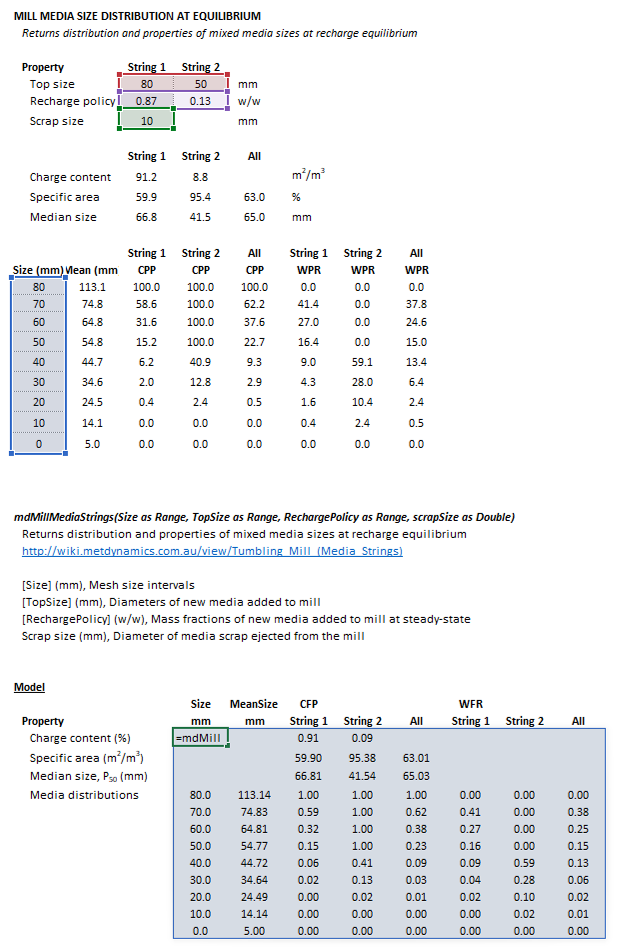Figure 1. Example showing the selection of the Size (blue frame), TopSize (red frame), RechargePolicy (purple frame), scrapSize (green frame), and Results (light blue frame) arrays in Excel.

SysCAD

Media strings are an optional calculation for grinding mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
MediaStrings
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
Requirements
NumStrings	Input	Number of media strings (i.e. media recharge sizes)
TopSize	Input	Diameter of the recharge media by string
Recharge	Input	Recharge policy, fractions of each media make-up size added to the mill when recharging.
Results
ChargeContent	Display	Fraction of each string in the combined charge at equilibrium.
SpecificArea	Display	Specific surface area of each media string and all strings combined.
Size	Display	Size of each interval in mesh series.
MedianSize	Display	Median particle diameter (P50), by string and for all strings combined.
MeanSize	Display	Geometric mean size of each interval in mesh series.
Cumulative	Display	Cumulative mass fraction passing size distribution of media at recharge equilibrium, by string and for all strings combined.
Retained	Display	mass fraction retained size distribution of media at recharge equilibrium, by string and for all strings combined.