Ball Mill (Overfilling)

Description

This article describes several methods for estimating the maximum volumetric flow capacity of an overflow ball mill, including the Shi (2016) and Arbiter (1991) approaches.

Model theory

Shi method

Figure 1. Overflow discharge tumbling mill profile showing Shi's assumed charge and slurry pool areas.

Shi (2016) estimated the residence time of an overflow ball mill by considering the volume of slurry present in the grinding media interstices and slurry pool.

This was accomplished by adopting Morrell's (1996) simplified charge geometry and calculating the volume of slurry resident in each of the areas A-C in Figure 1:

A. In the grinding media interstices above the slurry pool level

B. In the grinding media interstices below the slurry pool level

C. In the slurry pool

The total volume of slurry in the mill is therefore the sum of slurry in areas A-C.

Estimating the slurry volume in areas A-C requires definition of the simplified charge geometry and slurry pool level for the mill in question.

Charge position

The simplified charge geometry is defined by three parameters:

• the angular position of the toe of the charge, $\theta _{\rm {t}}$ (rad),
• the angular position of the shoulder charge, $\theta _{\rm {s}}$ (rad), and
• the radius of the inner charge surface, $R_{i}$ (m).

Morrell's equations are used to define the charge position, i.e.

The position of the toe of the charge is defined as:

$\theta _{\rm {t}}=2.5307\left(1.2796-J_{\rm {t}}\right)\left(1-{\rm {e}}^{-19.42(\phi _{\rm {c}}-\phi )}\right)+{\frac {\pi }{2}}$

where:

• $J_{t}$ is the volumetric fraction of the mill occupied by balls and coarse rock (including void space and interstitial slurry) (v/v)
• $\phi$ (frac) is the theoretical fraction critical speed.

The fraction of critical speed at which centrifuging actually occurs, $\phi _{\rm {c}}$ (frac), is:

$\phi _{\rm {c}}={\begin{cases}\phi &\phi >0.35(3.364-J_{\rm {t}})\\0.35(3.364-J_{\rm {t}})&\phi \leq 0.35(3.364-J_{\rm {t}})\\\end{cases}}$

The position of the shoulder of the charge is:

$\theta _{\rm {s}}={\frac {\pi }{2}}-\left(\theta _{\rm {t}}-{\frac {\pi }{2}}\right){\big [}\left(0.336+0.1041\phi \right)+\left(1.54-2.5673\phi \right)J_{\rm {t}}{\big ]}$

The inner charge surface radius is:

$R_{i}=r_{\rm {m}}\left(1-{\frac {2\pi \beta J_{\rm {t}}}{2\pi +\theta _{\rm {s}}-\theta _{\rm {t}}}}\right)^{0.5}$

where $r_{\rm {m}}$ is the radius of the mill (m), and the fraction of total charge in the active region, $\beta$ (frac), is:

$\beta ={\frac {t_{\rm {c}}}{t_{\rm {f}}+t_{\rm {c}}}}$

The time taken to travel between the toe and shoulder of the charge during one revolution, $t_{\rm {c}}$ (s), is:

$t_{\rm {c}}={\frac {2\pi -\theta _{\rm {t}}+\theta _{\rm {s}}}{2\pi {\bar {N}}}}$

where the mean rotational rate, ${\bar {N}}$ (rev/s), is:

${\bar {N}}\approx {\frac {N_{\rm {m}}}{2}}$

and $N_{\rm {m}}$ is the rotational rate of the mill shell (rev/s).

The time taken to travel between the shoulder and toe of the charge in free flight during one revolution, $t_{\rm {f}}$ (s), is:

$t_{\rm {f}}\approx \left({\frac {2{\bar {r}}\left(\sin \theta _{\rm {s}}-\sin \theta _{\rm {t}}\right)}{g}}\right)^{0.5}$

where the mean radial position ${\bar {r}}$ (m), is:

${\bar {r}}={\frac {r_{\rm {m}}}{2}}\left[1+\left(1-{\frac {2\pi J_{\rm {t}}}{2\pi +\theta _{\rm {s}}-\theta _{\rm {t}}}}\right)^{0.5}\right]$

Slurry hold-up below pool level

The volume of slurry held up below the pool level in areas B and C, $V_{1}$ (m³), is:

$V_{1}=L_{\rm {m}}(S_{\rm {pool}}-S_{\rm {net\,ball}})$

where:

• $L_{\rm {m}}$ is effective mill length (m)
• $S_{\rm {pool}}$ is cross-sectional area of the slurry pool (m²)
• $S_{\rm {net\,ball}}$ is cross-sectional area occupied by the grinding media, excluding balls, below the slurry pool level(m²)

This implementation of the Shi model computes $L_{\rm {m}}$ as an effective mill length from:

$L_{\rm {m}}={\dfrac {V_{\rm {m}}}{\pi {R_{\rm {m}}}^{2}}}$

where $V_{\rm {m}}$ is the volume of the mill (m³) and $R_{\rm {m}}$ is the radius of the mill (m).

The volume of the mill is calculated as the sum of a cylinder and two right circular frustums:

$V_{\rm {m}}=\pi {R_{\rm {m}}}^{2}L+2\cdot {\bigg [}{\dfrac {\pi }{3}}(R_{\rm {m}}-R_{\rm {t}})\cdot \tan \alpha _{\rm {c}}\cdot \left({R_{\rm {m}}}^{2}+R_{\rm {m}}R_{\rm {t}}+{R_{\rm {t}}}^{2}\right){\bigg ]}$

where:

• $L$ is the length of the cylindrical (belly) section of the mill (m)
• $R_{\rm {t}}$ is the radius of the discharge trunnion (m)
• $\alpha _{\rm {c}}$ is the cone angle, measured as the angular displacement of the cone surface from the vertical direction (rad)

$S_{\rm {pool}}$ is computed from:

$S_{\rm {pool}}=0.5{R_{\rm {m}}}^{2}(\theta _{\rm {p}}-\sin \theta _{\rm {p}})$

$\theta _{\rm {p}}=\pi -2\alpha$

$\alpha =\arcsin \left({\dfrac {R_{\rm {t}}-\Delta h}{R_{\rm {m}}}}\right)$

where $R_{\rm {t}}$ is the radius of the discharge trunnion (m), and $\Delta h$ is the height of the slurry pool level over the trunnion lip (m).

The value of $\Delta h$ may be estimated as $0.67h$, where $h$ is the slurry height above the trunnion level inside the mill (m):

$h=k_{\mu }\cdot {\frac {1}{0.67}}\left({\frac {2Q}{\pi R_{\rm {t}}g^{0.5}}}\right)^{\frac {2}{3}}$

and:

• $k_{\mu }$ is an empirical coefficient related to the viscidity of the slurry (Morrell suggests $k_{\mu }\approx 2$, Shi applies $k_{\mu }=1$)
• $Q$ is the volumetric discharge rate of pulp from the mill (m³/s)
• $g$ is acceleration due to gravity (m/s²)

$S_{\rm {net\,ball}}$ is computed as:

$S_{\rm {net\,ball}}=0.5\theta _{\rm {b}}(1-\varepsilon _{\rm {d}})({R_{\rm {m}}}^{2}-{R_{\rm {t}}}^{2})$

$\theta _{\rm {b}}=2\pi -\alpha -\theta _{\rm {t}}$

where the dynamic charge porosity, $\varepsilon _{\rm {d}}$ (v/v), is:

$\varepsilon _{\rm {d}}=0.4+0.228\left[1-\exp \left(-0.315{\dfrac {\phi }{J_{\rm {t}}}}\right)\right]$

Slurry hold up above pool level

The volume of slurry held up in the grinding media interstices above the slurry pool level in area A, $V_{2}$ (m³), is:

$V_{2}=L_{\rm {m}}.\varepsilon _{\rm {d}}.S_{\rm {ball\,above\,pool}}$

where:

$S_{\rm {ball\,above\,pool}}=0.5(\theta _{\rm {s}}+\alpha )({R_{\rm {m}}}^{2}-{R_{\rm {t}}}^{2})$

Residence time and overfilling

The total volume of slurry hold up in the mill is $V_{\rm {total}}=V_{1}+V_{2}$ (m³).

The residence time of slurry in the mill, $t_{\rm {Res}}$ (s), is then:

$t_{\rm {Res}}={\dfrac {V_{\rm {total}}}{Q}}$

The axial velocity of slurry through the mill, $v_{\rm {ax}}$ (m/s), is:

$v_{\rm {ax}}={\dfrac {L_{\rm {m}}}{t_{\rm {Res}}}}$

Shi suggests the following residence time limits for overflow discharge ball mills (s):

$t_{\rm {Limit}}={\begin{cases}120{\text{ s}}&D_{\rm {m}}<5.9{\text{ m}}\\60{\text{ s}}&D_{\rm {m}}\geq 5.9{\text{ m}}\\\end{cases}}$

where $D_{\rm {m}}$ is the diameter of the mill (m), i.e. $D_{\rm {m}}=2R_{\rm {m}}$.

The maximum volumetric flow rate of the mill, $Q_{\rm {Max}}$ (m³/s), at the residence time limit $t_{\rm {Limit}}$ may be back-calculated using the above relations. However, as the height of slurry above the trunnion lip ($h$), and hence residence time ($t_{\rm {Res}}$), is a function of flow rate, no analytical solution is available and a numerical method is required for computation.

Arbiter method

Based on an analysis of industrial ball mills at five operations, Arbiter (1991) postulated that the axial velocity of pulp through a mill should be less than 2.2% of the mill's tangential velocity. The Arbiter Flow Number, $N_{\rm {q}}$, is defined as the ratio of axial to tangential velocity and is determined from:

$N_{\rm {q}}={\dfrac {\left({\dfrac {Q}{{\frac {\pi {D_{\rm {m}}}^{2}}{4}}(0.5-0.66J_{\rm {t}})}}\right)}{\pi N_{\rm {m}}D_{\rm {m}}}},\quad N_{\rm {q}}<0.0217$

where:

• $Q$ is the volumetric discharge rate of pulp from the mill (m3/s)
• $D_{\rm {m}}$ is the mill diameter (m)
• $J_{\rm {t}}$ is the volumetric charge fraction in the mill (v/v)
• $N_{\rm {m}}$ is mill rotational speed (rev/min)

The Arbiter Flow Number equation may be rearranged to yield the following relation for the maximum volumetric discharge rate of slurry from a mill prior to overloading, $Q_{N_{\rm {q}}}$ (m³/h):

$Q_{N_{\rm {q}}}=0.0217{\dfrac {\pi ^{2}}{4}}{D_{\rm {m}}}^{3}N_{\rm {m}}(0.5-0.66J_{\rm {t}})\cdot 3600$

Overfilling may be a risk if the actual volumetric flow rate to/from the mill approaches or exceeds $Q_{N_{\rm {q}}}$.

Additional notes

Shi estimated the residence times for a database of 121 overflow ball mills. These residence times are presented as cumulative frequency distributions in Figure 2, allowing the performance a given mill to be ranked against the database.

Figure 2. Cumulative frequency distribution of the volume-based residence time of 121 mills in Shi's database (after Shi, 2016).

Arbiter's relations were developed from a limited database of five mills, the largest of which was 5.3 m diameter x 6.4 m length.

Excel

Shi method

The Shi overflow discharge ball mill overfilling model may be invoked from the Excel formula bar with the following function call:

=mdMillOverfilling_Shi(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

$Parameters={\begin{bmatrix}D_{\rm {m}}{\text{ (m)}}\\L{\text{ (m)}}\\R_{\rm {t}}{\text{ (m)}}\\\alpha _{c}{\text{ (degrees)}}\\\phi {\text{ (frac)}}\\J_{\rm {t}}{\text{ (v/v)}}\\Q{\text{ (m}}^{3}{\text{/h)}}\\k_{\mu }\\\end{bmatrix}},\;\;\;\;\;\;mdMillOverfilling\_Shi={\begin{bmatrix}v_{\rm {ax}}{\text{ (m/s)}}\\t_{\rm {Res}}{\text{ (s)}}\\t_{\rm {Limit}}{\text{ (s)}}\\Q_{\rm {Max}}{\text{ (m}}^{3}{\text{/h)}}\\V_{1}{\text{ (m}}^{3}{\text{)}}\\V_{2}{\text{ (m}}^{3}{\text{)}}\\V_{\rm {total}}{\text{ (m}}^{3}{\text{)}}\\\end{bmatrix}}\;\;\;\;\;\;$

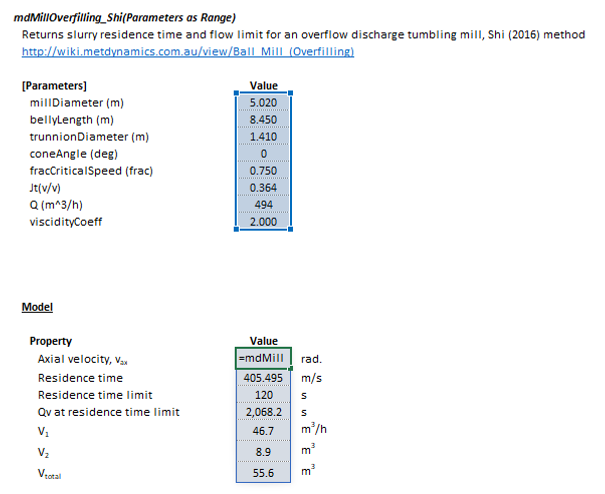Figure 3. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

Arbiter method

The Arbiter overflow discharge ball mill overfilling model may be invoked from the Excel formula bar with the following function call:

=mdMillOverfilling_Arbiter(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

$Parameters={\begin{bmatrix}D_{\rm {m}}{\text{ (m)}}\\\phi {\text{ (frac)}}\\J_{\rm {t}}{\text{ (v/v)}}\\\end{bmatrix}},\;\;\;\;\;\;mdMillOverfilling\_Arbiter={\begin{bmatrix}Q_{N_{\rm {q}}}{\text{ (m}}^{3}{\text{/h)}}\\\end{bmatrix}}\;\;\;\;\;\;$

Figure 4. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Ball Mill Overfilling Indicator model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Overfilling
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
Shi
MillDiameter	Input/Display	Diameter of the mill (inside liners).
BellyLength	Input/Display	Length of the cylindrical section (belly) of the mill (inside liners).
TrunnionDiameter	Input/Display	Diameter of the trunnion (inside liners).
ConeAngle	Input/Display	Angular displacement of the cone surface from the vertical direction.
FracCS	Input/Display	Fraction critical speed of the mill.
Jt	Input/Display	Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
ViscidityCoeff	Input	Coefficient of viscidity.
V1	Display	Volume of slurry below slurry pool level.
V2	Display	Volume of slurry above slurry pool level.
V1	Display	Total volume of slurry in charge and pool.
AxialVelocity	Display	Axial velocity of slurry flow through the charge and pool.
tRes	Display	Residence time of slurry in mill.
tLimit	Display	Shi's suggested lower limit of residence time for mill. Based on mill diameter.
Feed.SLQv	Display	Volumetric flow rate of slurry (solids + liquids) in mill feed.
Feed.SLQv.Limit	Display	Estimated volumetric flow rate of slurry (solids + liquids) in mill feed at tLimit.
Overfilled	True/False	Indicates if tRes is less than tLimit, i.e. mill is overfilled.
Arbiter
MillDiameter	Input/Display	Diameter of the mill (inside liners).
FracCS	Input/Display	Fraction critical speed of the mill.
Jt	Input/Display	Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
Feed.SLQv	Display	Volumetric flow rate of slurry (solids + liquids) in mill feed.
Feed.SLQv.NqLimit	Display	Estimated volumetric flow rate of slurry (solids + liquids) at Arbiters critical flow number limit.

See also

• Tumbling Mill (Power, Morrell Continuum)
• Perfect Mixing ball mill model
• Mill (Herbst-Fuerstenau)