Tumbling Mill (Media Trajectory)

Description

Figure 1. Example tumbling mill media trajectory, including Morrell Continuum charge position.

This article describes Powell's (1991) method for predicting the trajectory of the outer media elements in a tumbling mill.

The approach predicts the point of impact of media elements projected into free flight after transit down a lifter bar surface, based on element size, lifter bar geometry, mill diameter and mill rotational speed.

The tumbling mill media trajectory model is particularly useful when combined with an estimate of charge position (e.g. Morrell's method), which allows analyses such as:

• Identifying and mitigating the risks of shell liner damage from media impact through lifter bar (or mill) design
• Monitoring trajectory and point of impact changes with charge level, mill speed or liner and lifter bar wear in operational mills
• Limiting the maximum operating speed (and hence power and throughput) in a mill simulation or process control sub-systems

Model theory

This content is available to registered users. Please log in to view.

Excel

The tumbling mill media trajectory model may be invoked from the Excel formula bar with the following function call:

=mdMillPower_MillMediaTrajectory(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

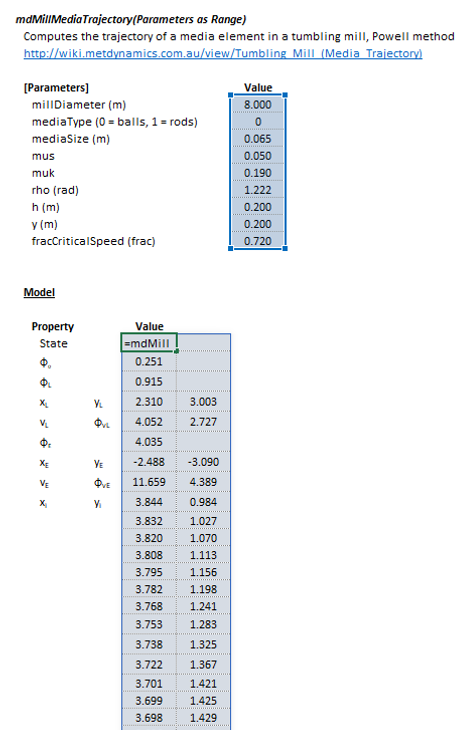
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

$Parameters={\begin{bmatrix}D{\text{ (m)}}\\{\text{Media type}}\\d{\text{ (m)}}\\\mu _{\rm {s}}\\\mu _{\rm {k}}\\\rho {\text{ (rad)}}\\h{\text{ (m)}}\\y{\text{ (m)}}\\C_{\rm {s}}(frac)\end{bmatrix}},\;\;\;\;\;\;mdMillPower\_MillMediaTrajectory={\begin{bmatrix}{\begin{bmatrix}{\text{State}}&-\\\end{bmatrix}}\\{\begin{bmatrix}\phi _{0}{\text{ (rad)}}&-\\\end{bmatrix}}\\{\begin{bmatrix}\phi _{\rm {L}}{\text{ (rad)}}&-\\\end{bmatrix}}\\{\begin{bmatrix}x_{\rm {L}}{\text{ (m)}}&y_{\rm {L}}{\text{ (m)}}\\v_{\rm {L}}{\text{ (m)}}&\phi _{v{\rm {L}}}{\text{ (rad)}}\\\end{bmatrix}}\\{\begin{bmatrix}\phi _{\rm {E}}{\text{ (rad)}}&-\\\end{bmatrix}}\\{\begin{bmatrix}x_{\rm {E}}{\text{ (m)}}&y_{\rm {E}}{\text{ (m)}}\\v_{\rm {E}}{\text{ (m)}}&\phi _{v{\rm {E}}}{\text{ (rad)}}\\\end{bmatrix}}\\{\begin{bmatrix}x_{0}{\text{ (m)}}&y_{0}{\text{ (m)}}\\\vdots &\vdots \\x_{n}{\text{ (m)}}&y_{n}{\text{ (m)}}\\\end{bmatrix}}\\\end{bmatrix}}\;\;\;\;\;\;$ where: $D$ is the mill diameter inside liners (m), i.e. $D=2R$ $d$ is the media element diameter (m), i.e. $d=2a$ ${\text{Media type}}$ is the type of media element, balls or rods (0 = Balls, 1 = Rods) $C_{\rm {s}}$ is the fraction critical speed of the mill (frac) and: ${\text{State}}$ is a text string that describes the motion of the media element $n$ is the number of trajectory points for plotting

Figure 7. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The media trajectory model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
MediaTraj
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
Requirements
MillDiameter	Input/Display	Diameter of the mill (inside liners).
FracCS	Input/Display	Fraction critical speed of the mill.
MediaType	Ball/Rod	Type of media element, balls or rods.
MediaSize	Display	Diameter of the media element.
mus	Input	Coefficient of static friction.
muk	Input	Coefficient of kinematic friction.
rho	Input	Lifter face angle, angle between the face surface and the base of the lifter bar.
h	Input	Height of the lifter bar.
2y	Input	Width of the lifter bar.
Results
PointOfEquilibrium
PositionAngle / Phi	Display	Angular position of the point of equilibrium.
LeavesLifter
PositionAngle / Phi	Display	Angular position of the point where the media element leaves the lifter.
X	Display	Cartesian x coordinate of the point where the media element leaves the lifter.
Y	Display	Cartesian y coordinate of the point where the media element leaves the lifter.
Velocity / V	Display	Velocity of the media element at the point where it leaves the lifter.
VelocityAngle / PhiV	Display	Angular direction of the velocity of the media element at the point where it leaves the lifter.
ImpactsShell
PositionAngle / Phi	Display	Angular position of the point where the media element impacts the mill shell.
X	Display	Cartesian x coordinate of the point where the media element impacts the mill shell.
Y	Display	Cartesian y coordinate of the point where the media element impacts the mill shell.
Velocity / V	Display	Velocity of the media element at the point where it impacts the mill shell.
VelocityAngle / PhiV	Display	Angular direction of the velocity of the media element at the point where it impacts the mill shell.
State	Display	Text description of the motion of the media element. Possible values are: "Element is projected into free flight from point of equilibrium." "Element slides to end of the lifter and is then projected into free flight." "Element slides and is projected into free flight before the end of the lifter." "Element rolls to the end of the lifter and is projected into free flight." "Element rolls then slides to the end of the lifter before being projected into free flight." "Element rolls then slides and is projected into free flight before the end of the lifter." "Element rolls and is projected into free flight before the end of the lifter."
Trajectory
ShowTrajectory	CheckBox	If enabled, the (x, y) coordinate data of the element trajectory is displayed below.
TrajectoryData		Copies the full set of trajectory coordinates to the Windows clipboard in CSV format.
Point, X, Y	Display	X and Y coordinates of the media element trajectory, from the point of equilibrium to point of impact with the mill shell. Only visible if ShowTrajectory is enabled above.

See also

• Morrell Continuum model