Ball Mill (Perfect Mixing, Dynamic)

Description

This article describes a dynamic implementation of the Perfect Mixing ball mill model outlined by Napier-Munn et al. (1996).

The dynamic version uses the same underlying theory and structure as the steady-state Perfect Mixing ball mill model. For a full description of the steady-state model, see Ball Mill (Perfect Mixing).

Model theory

The dynamic Perfect Mixing model is based on a population balance of particles entering the mill, breaking into smaller sizes, and discharging as product. For a mill operating in unsteady-state, the diagram in Figure 1 below represents the balance for a given size fraction:

Figure 1. Schematic diagram of the population balance adopted by the dynamic Perfect Mixing model.

The dynamic population balance is described mathematically as:

${\frac {ds_{i}(t)}{dt}}=f_{i}-D_{i}s_{i}+\sum _{j=1}^{i-1}A_{ij}R_{j}s_{j}-(R_{i}s_{i}-A_{ii}R_{i}s_{i})$

$p_{i}=D_{i}s_{i}$

where:

• $i$ is the index of the size interval, $i=\{1,2,\dots ,n\}$, $n$ is the number of size intervals
• $f_{i}$ is the mass feed rate of solids in size interval $i$
• $p_{i}$ is the mass product rate of solids in size interval $i$
• $s_{i}$ is the mass of solids in the mill load in size interval $i$
• $R_{i}$ is the breakage rate of solids in the mill load in size interval $i$
• $D_{i}$ is the rate of discharge from the mill of solids in size interval $i$
• $A_{ij}$ is the Appearance function, the distribution of particle mass arising from the breakage of a parent particle in size interval $j$ into progeny of size interval $i$

Unlike the steady-state version, the load component $s_{i}$ cannot be eliminated from the equation, nor can the $R_{i}$ and $D_{i}$ components be combined into a single $R_{i}/D_{i}$ term. Therefore, the breakage and discharge rates $R_{i}$ and $D_{i}$ must be specified separately as inputs to the dynamic model.

Finally, an unsteady-state mill simulation must also consider the retention of liquids in the load:

${\frac {ds_{\rm {w}}(t)}{dt}}=f_{\rm {w}}-D_{\rm {w}}s_{\rm {w}}$

where:

• $s_{\rm {w}}$ is the load mass of water in the mill
• $f_{\rm {w}}$ is the mass feed rate of water into the mill
• $D_{\rm {w}}$ is the discharge rate of water from the mill, normally assumed to equal the value of $D_{i}$ at the finest size interval.

Time step discretisation

The unsteady-state Perfect Mixing differential equation is numerically solved by a discretised time stepping approach (i.e. Euler's method). The change in load mass in a size fraction $\Delta s_{i}$ during a sufficiently small time increment $\Delta t=t_{n+1}-t_{n}$ is:

$\Delta s_{i}=\left(f_{i}-D_{i}s_{i}+\sum _{j=1}^{i-1}A_{ij}R_{j}s_{j}-(R_{i}s_{i}-A_{ii}R_{i}s_{i})\right).\Delta t$

Similarly, for liquids:

$\Delta s_{w}=\left(f_{w}-D_{w}s_{w}\right).\Delta t$

The time stepping approach is a convenient numerical approximation to the solution of the unsteady-state Perfect Mixing population balance differential equation. The approach is, however, subject to several limitations:

• The mass of particles separately discharged from or broken out of a size interval in a time step cannot exceed the mass of particles actually present in that size interval.
• Similarly, the overall maximum discharge flow rate of pulp from the mill cannot exceed the total volume of pulp in the mill in a time step.

The time step size used internally by the model is automatically reduced to ensure the breakage, discharge and pulp flow rate limits per step are not exceeded. This is achieved by computing a number of sequential sub-steps at the reduced internal step size for each requested external step.

This is useful if the either a fixed time step specified by an application is too large (e.g. SysCAD) or a numerical solution is desired in as few steps as possible (e.g. Excel). The automatic time step adjustment is largely invisible to the user and manifests only as a slightly slower execution speed.

The calculated time step size may be overridden with a larger user-specified sub-step count if increased accuracy in the numerical approximation is desired.

Breakage rate

Figure 2. Schematic of a tumbling mill showing key dimensions.

The breakage function, $R_{i}$, is an input parameter for the dynamic Perfect Mixing model, replacing the $R_{i}/D_{i}$ term appearing in the steady-state version.

The steady-state Perfect Mixing model scaling factors for mill diameter, load fraction, fraction critical speed, work index and ball diameter are assumed to be explicitly related to the breakage rate and are applied to the $R_{i}$ function here, i.e.:

$R_{\rm {Sim}}=R_{\rm {Orig}}\cdot f_{\rm {D}}\cdot f_{\rm {LF}}\cdot f_{\rm {CS}}\cdot f_{\rm {WI}}\cdot f_{\rm {Db}}$

The scaling factors are defined as:

${\begin{array}{lll}f_{\rm {D}}={\sqrt {\dfrac {D_{\rm {Sim}}}{D_{\rm {Orig}}}}},&&&f_{\rm {LF}}={\dfrac {(1-{\rm {LF}}_{\rm {Sim}}).{\rm {LF}}_{\rm {Sim}}}{(1-{\rm {LF}}_{\rm {Orig}}).{\rm {LF}}_{\rm {Orig}}}},\\f_{\rm {CS}}={\dfrac {(C_{\rm {s}})_{\rm {Sim}}}{(C_{\rm {s}})_{\rm {Orig}}}},&&&f_{\rm {WI}}=\left({\dfrac {{\rm {WI}}_{\rm {Orig}}}{{\rm {WI}}_{\rm {Sim}}}}\right)^{0.8},\\\end{array}}$

$f_{\rm {Db}}={\begin{cases}{\dfrac {Db_{\rm {Orig}}}{Db_{\rm {Sim}}}}&{\text{for }}x<x_{\rm {m(small)}},\;\;\;x_{\rm {m(small)}}=\min {\left(K.Db_{\rm {Orig}}^{2},K.Db_{\rm {Sim}}^{2}\right)}\\\left({\dfrac {Db_{\rm {Orig}}}{Db_{\rm {Sim}}}}\right)^{2}&{\text{for }}x\geq x_{\rm {m(large)}},\;\;\;x_{\rm {m(large)}}=\max {\left(K.Db_{\rm {Orig}}^{2},K.Db_{\rm {Sim}}^{2}\right)}\\\end{cases}}$

where:

• $D$ is mill diameter (m)
• ${\rm {LF}}$ is load fraction, the load volume as a fraction of mill volume (v/v)
• $C_{\rm {s}}$ is the fraction critical speed of the mill (frac)
• ${\rm {WI}}$ is the Bond Ball Work Index of the ore (kWh/t)
• $Db$ is the ball diameter (mm)
• $x$ is the diameter of a particle of size interval $i$ (mm)
• $K$ is the maximum breakage rate factor which relates ball size and the size at which $R_{i}/D_{i}^{*}$ is maximum, i.e. $x_{m}=K.Db^{2}$
• $f_{\rm {Db}}$ is interpolated for $x_{\rm {m(small)}}<x<x_{\rm {m(large)}}$

and the ${\rm {Orig}}$ subscript refers to the original mill from which $R_{i}/D_{i}^{*}$ was derived and ${\rm {Sim}}$ refers to the mill being simulated (scaled).

The discharge rate scaling factor, $D^{*}$, is excluded from the breakage rate scaling term and is dealt with separately within the model (see Slurry filling and discharge, below).

Discharge rate

The classical Leung definition of discharge rate of solids from a perfectly mixed mill is:

$p_{i}=D_{i}.s_{i}$

where:

$D_{i}=d_{\rm {max}}.C_{i}$

$C_{i}={\begin{cases}1&{\bar {d}}_{i}<x_{\rm {m}}\\1-{\dfrac {\ln {\bar {d}}_{i}-\ln x_{\rm {m}}}{\ln x_{\rm {g}}-\ln x_{\rm {m}}}}&x_{\rm {m}}<{\bar {d}}_{i}<x_{\rm {g}}\\0&{\bar {d}}_{i}>x_{\rm {g}}\\\end{cases}}$

and:

• $d_{\rm {max}}$ is the fraction of load presented to the mill discharge per unit of time (h^-1)
• $C_{i}$ is the classification function, the fraction of particles of size $i$ reporting to the mill product (frac)
• ${\bar {d}}_{i}$ is the geometric mean size of particles in size interval $i$ (mm)
• $x_{\rm {m}}$ is the particle size below which all mass in the size interval reports to mill product (mm), i.e. like water
• $x_{\rm {g}}$ is the largest particle size which can report to mill product (mm)

Appearance function

The appearance function describes the mass-by-size distribution of progeny particles resulting from the breakage of parent particles.

The appearance function may be specified for a particular ore. Alternatively, the default Broadbent-Callcott appearance function may be used, which is defined as:

$A_{ij}={\frac {1-\exp \left(-{\dfrac {d_{i}}{d_{j}}}\right)}{1-\exp(-1)}}$

where $d_{i}$ is the breakage product particle size and $d_{j}$ is the original particle size.

Internal mesh series

The Perfect Mixing mill model is formulated internally with a geometric progression of 31 mesh sizes at ${\sqrt {2}}$ intervals. Feed and product size fractions are automatically converted to and from the internal mesh series during model computation. The ${\sqrt {2}}$ size intervals allow the appearance function to be specified as a one-dimensional matrix, rather than the two dimensional form defined above, since

$A_{ij}=A_{i-j}$

when the intervals are so spaced.

Multi-component modelling

The original Perfect Mixing model formulation only considered the properties of a single ore type.

This implementation applies different appearance functions and breakage rate scaling factors to separate population balance computations for each ore type in the feed.

Slurry filling and discharge

The unsteady-state population balance and liquid hold-up models described above compute the quantity of slurry in the mill at each discrete time step.

The mill, whether grate of overflow discharge configured, may be in one of a number of slurry filling states at any time:

1. Empty (balls only, no slurry)
2. Charge void space partially filled with slurry
3. Charge void space fully filled with slurry and a slurry pool formed at the toe of the tumbling charge
4. Charge void space fully filled, slurry pool is overflowing the trunnion of the mill

The slurry filling states states are illustrated visually in Figure 3 below:

Figure 3. Overflow discharge mill slurry filling states, profile view.

1. Empty (balls only, no slurry).

2. Charge void space partially filled with slurry.

3. Charge void space fully filled with slurry and a slurry pool formed at the toe of the tumbling charge.

4. Charge void space fully filled, slurry pool is overflowing the discharge trunnion lip.

The filling states are numbered are in progressive order as a mill is filled from an empty state. A mill may transition between the states in forward or backward direction during dynamic simulation as the feed and milling conditions change.

Discharge flow from a mill will commence from different filling states depending on whether the mill is grate or overflow configured. There is no product from the mill prior to the commencement of discharge flow and hence the discharge rate, $D_{i}$, is zero. During this period, the dynamic population balance reduces to a batch mill formulation (with or without feed), as outlined by Whiten (1974):

${\frac {ds_{i}(t)}{dt}}=f_{i}+\sum _{j=1}^{i-1}A_{ij}R_{j}s_{j}-(R_{i}s_{i}-A_{ii}R_{i}s_{i})$

Overflow discharge mill

Slurry will not discharge from an overflow mill until filling state 4, once the slurry pool level has risen above the trunnion lip. The volumetric discharge rate of pulp from an overflow mill is then, for practical purposes, equal to the instantaneous volumetric feed rate.

The quantity of slurry in the mill at the point of trunnion overflow is determined by the mill dimensions and charge geometry. The method described by Shi (2016) is used to compute the volumetric sum of slurry within the charge void space and slurry pool at the overflow condition.

The model computes the value of $d_{\rm {max}}$ to ensure the total flow rate of water plus solids classified for discharge matches the required product pulp outflow rate (i.e. the feed rate) for an overflow mill.

Grate discharge mill

Slurry will commence discharging from a grate configured mill from step 2, once the slurry level inside the charge exceeds the level of the outermost apertures in the grate. The discharge rate of a grate mill then increases as the level of slurry held-up in the mill increases.

The method of Morrell and Stephenson (1996) is used to compute the volumetric discharge flow rate of slurry for mill filling states 2 and 3:

${\begin{array}{ll}Q_{\rm {m}}=k_{\rm {m}}{J_{\rm {pm}}}^{2}\gamma ^{2.5}A\phi ^{-1.34}D^{0.5}&J_{\rm {pm}}\leq J_{\rm {max}}\\Q_{\rm {t}}=k_{\rm {t}}J_{\rm {pt}}\gamma ^{2}AD^{0.5}&J_{\rm {p}}>J_{\rm {max}}\\&J_{\rm {pt}}=J_{\rm {p}}-J_{\rm {max}}\\&J_{\rm {max}}=0.5J_{\rm {t}}-J_{\rm {po}}\\&J_{\rm {po}}=0.33(1-r_{\rm {n}})\\&J_{\rm {p}}=J_{\rm {pg}}-J_{\rm {po}}\\\end{array}}$

where

• $Q_{\rm {m}}$ and $Q_{\rm {t}}$ are the volumetric discharge rates of slurry through the grinding media zone and slurry pool, respectively (m³/h)
• $k_{\rm {m}}$ and $k_{\rm {t}}$ are the slurry discharge coefficients for the grinding media zone and slurry pool, respectively
• $J_{\rm {pm}}$ is the net fractional slurry hold-up in the grinding media interstices (v/v)
• $J_{\rm {pt}}$ is the net fractional slurry hold-up in the slurry pool (v/v)
• $\gamma$ is the open area weighted mean radial position of the grate apertures (m/m)
• $A$ is the total open area of grate apertures (m²)
• $D$ is the mill diameter (m)
• $\phi$ is the fraction critical speed of the mill (frac)
• $J_{\rm {p}}$ is the net fraction of mill volume occupied by slurry (v/v)
• $J_{\rm {max}}$ is the maximum net fractional slurry hold-up in the grinding media zone (v/v)
• $J_{\rm {t}}$ is the fraction of mill volume occupied by grinding media, including associated interstices (v/v)
• $J_{\rm {po}}$ is the dead fraction of mill volume which is occupied by slurry before discharge commences (v/v)
• $J_{\rm {pg}}$ is gross fraction of mill volume occupied by slurry (v/v)
• $r_{\rm {n}}$ is the relative radial position of the outermost grate apertures (m/m)

The model computes the value of $d_{\rm {max}}$ to ensure the flow rate of water and solids $<x_{\rm {m}}$ discharged from the mill matches the flow rate required by the Morrell and Stephenson relations at the current slurry hold-up level.

If the mill continues to fill due to excessive feed rate or insufficient discharge capacity, the slurry level will eventually overflow the trunnion lip (filling state 4). Once this occurs, the overflow discharge method described above is used to determine pulp outflow (i.e. $d_{\rm {max}}$ computed such that mill discharge flow rate = mill feed flow rate).

Power draw

Figure 4. Simplified charge and slurry pool shapes.

The dynamic Perfect Mixing ball mill model computes the volume of slurry in the mill at each time step according to the unsteady-state population balance, water hold-up, breakage and discharge relations described above.

Estimation of the power draw of the mill must then take into account the instantaneous volume of slurry that is either within the charge void space or in the pool of excess slurry outside the charge.

The tumbling mill power draw model proposed by Hilden and Powell (2018) is based on earlier work by Morrell (1996, 2016) and computes the volume of slurry occupying the four areas illustrated in Figure 4:

A. In the grinding media interstices above the slurry pool level

B. In the grinding media interstices below the slurry pool level

C. In the annular sector at the toe of the charge

D. In the circular segment settled across the centre of the mill

Slurry in areas A - C contributes to the power draw of the mill. Slurry in area D is evenly distributed on each side of the vertical centreline of the mill and therefore does not contribute to power draw.

This makes the Hilden and Powell model it a convenient formulation for use by the dynamic Perfect Mixing mill model, which is continuously computing the total volume of slurry in the mill during simulation.

Additional notes

The Leung classification function applies for both grate and overflow discharge mills:

• Grate mills are specified according to the aperture dimensions of installed discharge grates.
• For overflow mills, the maximum particle size reporting to product may be an appropriate estimate of $x_{\rm {g}}$ if mill contents are not available.
• Alternatively, overflow mills may be simplified and classification effects ignored by setting $C_{i}=1$ for all $i$, if preferred.
• A value of 1 mm for $x_{\rm {m}}$ may be an adequate choice for both mill discharge configurations.

Excel

The Perfect Mixing ball mill model is not implemented in Excel in dynamic form for practical purposes. Excel is not an ideal platform for dynamic simulation and SysCAD (or similar) is preferred.

The dynamic model is, however, included in Excel in a run-to-steady-state mode where all feed and input parameters are fixed and time steps are progressed until the computed load and discharge stabilises.

This mode is useful for extracting separated $R_{i}$ and $D_{i}$ functions from steady-state data such as plant surveys or other model calibrations (including the steady-state Perfect Mixing ball mill model).

The run-to-steady-state dynamic Perfect Mixing ball mill model may be invoked from the Excel formula bar with the following function call:

=mdUnit_BallMill_PerfectMixingRiDi(Parameters as Range, Size as Range, MillFeed as Range, OreSG As Range, Appearance as Range, WorkIndexSim as Range, RKnotPositions as Range, RKnotsOrig as Range, Classification as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

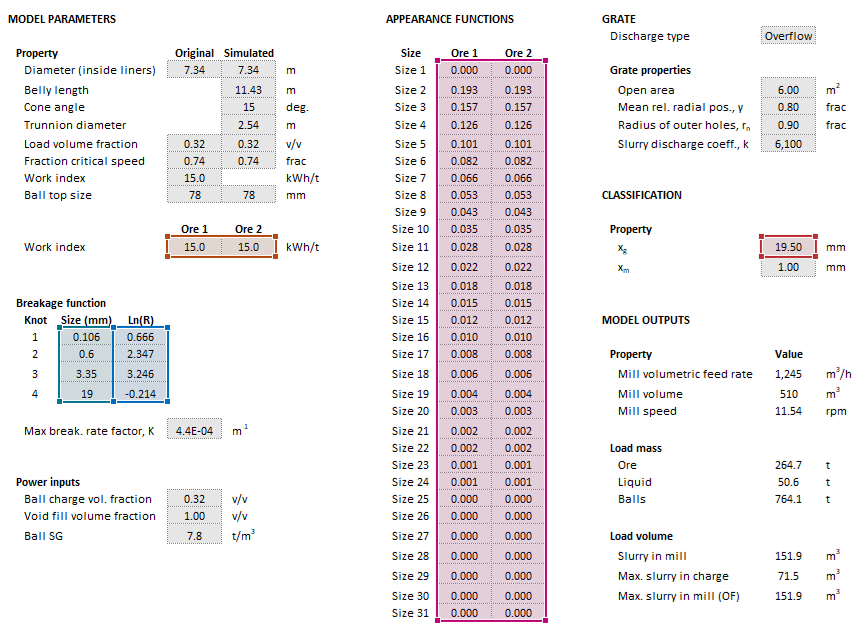
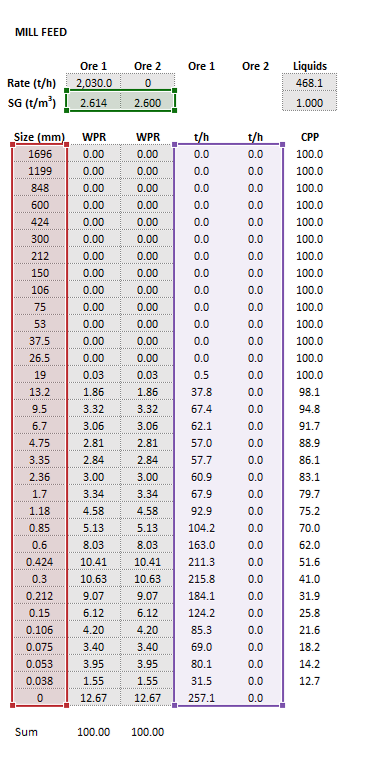
Inputs

The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row ($i$) x column ($j$) format:

$Parameters={\begin{bmatrix}D_{\rm {Orig}}{\text{ (m)}}\\{\rm {LF}}_{\rm {Orig}}{\text{ (v/v)}}\\(C_{\rm {s}})_{\rm {Orig}}{\text{ (frac)}}\\{\rm {WI}}_{\rm {Orig}}{\text{ (kWh/t)}}\\Db_{\rm {Orig}}{\text{ (mm)}}\\D_{\rm {Sim}}{\text{ (m)}}\\{\rm {LF}}_{\rm {Sim}}{\text{ (v/v)}}\\(C_{\rm {s}})_{\rm {Sim}}{\text{ (frac)}}\\{\rm {WI}}_{\rm {Orig}}{\text{ (kWh/t)}}\\Db_{\rm {Sim}}{\text{ (mm)}}\\K\\L{\text{ (m)}}\\\alpha _{c}{\text{ (deg.)}}\\D_{\rm {t}}{\text{ (m)}}\\J_{\rm {B}}{\text{ (v/v)}}\\U{\text{ (v/v)}}\\\rho _{\rm {B}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\(Q_{\rm {M,F}})_{\rm {L}}{\text{ (t/h)}}\\\rho _{\rm {L}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\{\text{Classification method}}\\x_{\rm {m}}{\text{ (mm)}}\\{\text{Discharge type}}\\A{\text{ (m}}^{\text{2}}{\text{)}}\\\gamma {\text{ (m/m)}}\\r_{\rm {n}}{\text{ (m/m)}}\\k_{\rm {m}}\\k_{\rm {t}}\\{\text{User overflow volume (m}}^{\text{3}}{\text{)}}\\\end{bmatrix}},\;\;\;\;\;\;Size={\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{n}{\text{ (mm)}}\\\end{bmatrix}},\;\;\;\;\;\;MillFeed={\begin{bmatrix}(Q_{\rm {M,F}})_{11}{\text{ (t/h)}}&\dots &(Q_{\rm {M,F}})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{\rm {M,F}})_{n1}{\text{ (t/h)}}&\dots &(Q_{\rm {M,F}})_{nm}{\text{ (t/h)}}\\\end{bmatrix}},\;\;\;\;\;\;OreSG={\begin{bmatrix}(\rho _{\rm {S}})_{1}{\text{ (t/m}}^{\text{3}}{\text{)}}&\dots &(\rho _{\rm {S}})_{m}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\end{bmatrix}}$

$Appearance={\begin{bmatrix}{\begin{bmatrix}A_{1}{\text{ (frac)}}\\\vdots \\A_{31}{\text{ (frac)}}\\\end{bmatrix}}_{1}\dots {\begin{bmatrix}A_{1}{\text{ (frac)}}\\\vdots \\A_{31}{\text{ (frac)}}\\\end{bmatrix}}_{m}\end{bmatrix}},\;\;\;\;\;\;{\rm {WI}}_{\rm {Sim}}={\begin{bmatrix}{\rm {WI}}_{1}{\text{ (kWh/t)}}&\dots &{\rm {WI}}_{m}{\text{ (kWh/t)}}\\\end{bmatrix}},\;\;\;\;\;\;RKnotPositions={\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{k}{\text{ (mm)}}\\\end{bmatrix}},\;\;\;\;\;\;RKnotOrig={\begin{bmatrix}\ln \left({\frac {R}{D^{*}}}\right)_{1}\\\vdots \\\ln \left({\frac {R}{D^{*}}}\right)_{k}\\\end{bmatrix}}$

$Classification={\begin{cases}{\begin{bmatrix}C_{1}{\text{ (frac)}}\\\vdots \\C_{31}{\text{ (frac)}}\\\end{bmatrix}}&{\mbox{if Classification method}}=0{\mbox{ (User)}}\\x_{\rm {g}}&{\mbox{if Classification method}}=1{\mbox{ (Leung)}}\\\end{cases}}$

where:

• $L$ is the mill (belly) length
• $\alpha _{c}$ is angle between the cone end surface and the vertical direction (degrees)
• $D_{\rm {t}}$ is the diameter of the discharge trunnion (m)
• $J_{\rm {B}}$ is the ball charge volume fraction (often $J_{\rm {B}}={\rm {LF}}$) (v/v)
• $U$ is the void fill fraction, the volumetric fraction of grinding media interstitial void space occupied by slurry (v/v)
• $\rho _{\rm {B}}$ is the Specific Gravity or density of the ball media (excluding void space) (- or t/m³)
• $(Q_{\rm {M,F}})_{\rm {L}}$ is the mass flow feed rate of liquids into the mill (t/h)
• $\rho _{\rm {L}}$ is the Specific Gravity or density of liquids in the feed (- or t/m³)
• ${\text{Classification method }}$ is the method used to defined the classification-by-size to discharge, 0 = User-defined partition or 1 = Leung method
• ${\text{Discharge type}}$ is discharge configuration, 0 = Grate discharge, 1 = Overflow discharge at trunnion height, 2 = Overflow discharge at user-defined slurry filling volume
• ${\text{User overflow volume}}$ is the user-specified slurry filling volume at which overflow commences (if ${\text{Discharge type}}=2$) (m³)
• $m$ is the number of ore types
• $k$ is the number of breakage rate per discharge rate knots
• $Q_{\rm {M,F}}$ is feed mass flow rate (t/h)
• $\rho _{\rm {S}}$ is Specific Gravity or density (- or t/m³)

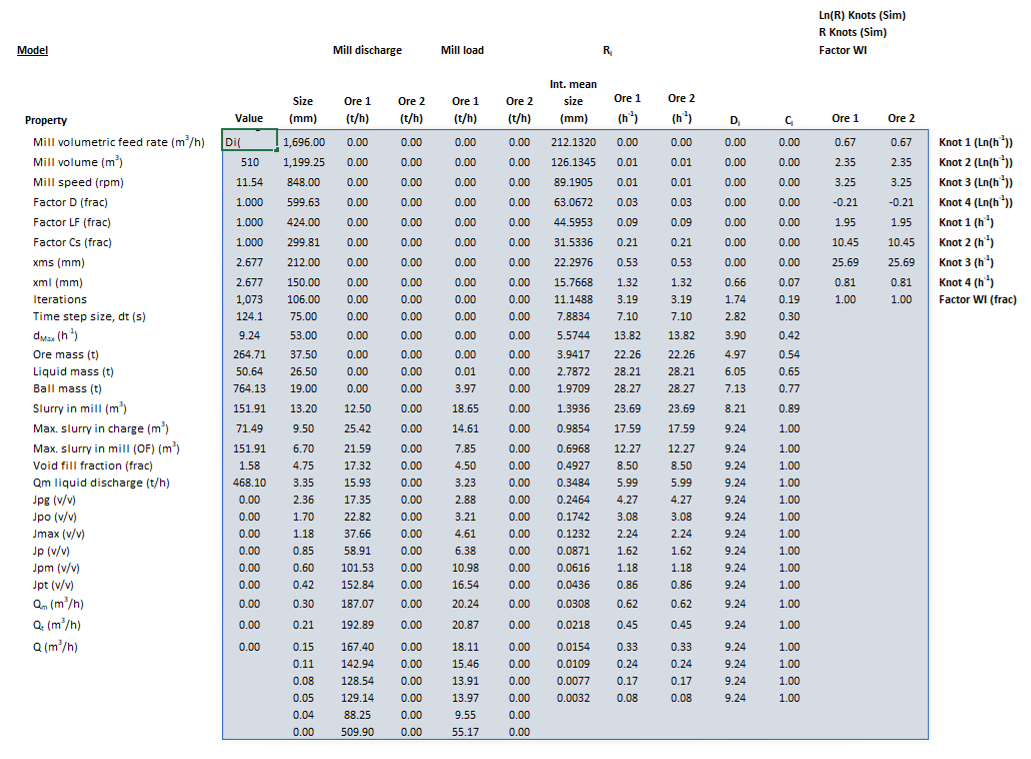
Results

The results are displayed in Excel as an array corresponding to the matrix notation below:

$mdUnit\_BallMill\_PerfectMixing\_RiDi={\begin{bmatrix}{\begin{bmatrix}Q_{\rm {V,F}}{\text{ (m}}^{\text{3}}{\text{/h)}}\\V{\text{ (m}}^{\text{3}}{\text{)}}\\N{\text{ (rpm)}}\\f_{D}{\text{ (-)}}\\f_{\rm {LF}}{\text{ (-)}}\\f_{\rm {CS}}{\text{ (-)}}\\x_{\rm {m(small)}}{\text{ (mm)}}\\x_{\rm {m(large)}}{\text{ (mm)}}\\{\text{Iterations}}\\dt{\text{ (s)}}\\d_{\rm {max}}{\text{ (h}}^{\text{-1}}{\text{)}}\\{\text{Ore mass (t)}}\\{\text{Liquid mass (t)}}\\{\text{Ball mass (t)}}\\{\text{Slurry in mill (m}}^{\text{3}}{\text{)}}\\{\text{Max. slurry in charge (m}}^{\text{3}}{\text{)}}\\{\text{Max. slurry in mill (OF) (m}}^{\text{3}}{\text{)}}\\U{\text{ (frac)}}\\(Q_{\rm {M,P}})_{\rm {L}}{\text{ (t/h)}}\\J_{\rm {pg}}{\text{ (v/v)}}\\J_{\rm {po}}{\text{ (v/v)}}\\J_{\rm {max}}{\text{ (v/v)}}\\J_{\rm {p}}{\text{ (v/v)}}\\J_{\rm {pm}}{\text{ (v/v)}}\\J_{\rm {pt}}{\text{ (v/v)}}\\Q_{\text{m}}{\text{ (m}}^{\text{3}}{\text{/h)}}\\Q_{\rm {t}}{\text{ (m}}^{\text{3}}{\text{/h)}}\\Q{\text{ (m}}^{\text{3}}{\text{/h)}}\\\end{bmatrix}}&{\begin{array}{cccccccc}{\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{n}{\text{ (mm)}}\end{bmatrix}}&{\begin{bmatrix}(Q_{\rm {M,P}})_{11}{\text{ (t/h)}}&\dots &(Q_{\rm {M,P}})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{\rm {M,P}})_{n1}{\text{ (t/h)}}&\dots &(Q_{\rm {M,P}})_{nm}{\text{ (t/h)}}\\\end{bmatrix}}&{\begin{bmatrix}M_{11}{\text{ (t/h)}}&\dots &M_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\M_{n1}{\text{ (t/h)}}&\dots &M_{nm}{\text{ (t/h)}}\\\end{bmatrix}}&{\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{31}{\text{ (mm)}}\\\end{bmatrix}}&{\begin{bmatrix}R_{11}\left({\text{h}}^{\text{-1}}\right)&\dots &R_{1m}\left({\text{h}}^{\text{-1}}\right)\\\vdots &\ddots &\vdots \\R_{31,1}\left({\text{h}}^{\text{-1}}\right)&\dots &R_{31m}\left({\text{h}}^{\text{-1}}\right)\\\end{bmatrix}}&{\begin{bmatrix}D_{1}\left({\text{h}}^{\text{-1}}\right)\\\vdots \\D_{31}\left({\text{h}}^{\text{-1}}\right)\\\end{bmatrix}}&{\begin{bmatrix}C_{1}{\text{ (frac)}}\\\vdots \\C_{31}{\text{ (frac)}}\\\end{bmatrix}}&{\begin{bmatrix}\ln R_{11}&\dots &\ln R_{1m}\\\vdots &\ddots &\vdots \\\ln R_{k1}&\dots &\ln R_{km}\\\end{bmatrix}}\\&&&&&&&{\begin{bmatrix}R_{11}\left({\text{h}}^{\text{-1}}\right)&\dots &R_{1m}\left({\text{h}}^{\text{-1}}\right)\\\vdots &\ddots &\vdots \\R_{k1}\left({\text{h}}^{\text{-1}}\right)&\dots &R_{km}\left({\text{h}}^{\text{-1}}\right)\\\end{bmatrix}}\\&&&&&&&{\begin{bmatrix}(f_{\rm {WI}})_{1}&\dots &(f_{\rm {WI}})_{m}\end{bmatrix}}\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\&&&&&&\\\end{array}}\end{bmatrix}}$

where:

• $Q_{\rm {V,f}}$ is the flow rate of pulp into the mill (m³/h)
• $V$ is the total volume inside the mill, calculated as the sum of a cylinder and two frustums (m³)
• $N$ is the rotational rate of the mill (rpm)
• ${\text{Iterations}}$ is the number of time steps required to reach steady-state
• $dt$ is the size of the discretised time step calculated by the model, $\Delta t$ (s)
• ${\text{Ore mass}}$ is the total mass of ore in the mill at steady-state (t)
• ${\text{Liquid mas}}$ is the mass of liquids in the mill at steady-state (t)
• ${\text{Ball mass}}$ is the mass of balls in the mill at steady-state (t)
• ${\text{Slurry in mill}}$ is the volume of slurry in the mill at steady-state (m³)
• ${\text{Max. slurry in charge}}$ is the maximum volume of slurry that can occupy the charge void space before forming a slurry pool (m³)
• ${\text{Max. slurry in mill (OF)}}$ is the maximum volume of slurry in the mill before trunnion overflow commences (m³)
• $(Q_{\rm {M,P}})_{\rm {L}}$ is the discharge mass flow rate of liquids from the mill (t/h)
• $Q_{\rm {M,P}}$ is product mass flow rate (t/h)
• $M$ is the mass of solids in the mill (t)

Example

The images below show the selection of input arrays and output results in the Excel interface.

Figure 5. Example showing the selection of the Parameters (blue frame) array in Excel.

Figure 6. Example showing the selection of the Appearance (pink frame), RKnotPositions (teal frame), RKnotsOrig (blue frame), WorkIndexSim (dark red frame), Classification (Leung, $x_{\rm {g}}$) (red frame) arrays in Excel.

Figure 7. Example showing the selection of the Size (red frame), OreSG (green frame) and MillFeed (purple frame) arrays in Excel.

Figure 8. Example showing the outline of the Results (light blue frame) array in Excel.

SysCAD

The SysCAD interface for Dynamic mode is described below. For steady-state, see Ball Mill (Perfect Mixing).

MD_Mill page

The first tab page in the access window will have this name.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Tag	Display	This name tag may be modified with the change tag option.
Condition	Display	OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount	Display	The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc	Display	This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here. If this field is blank, then SysCAD will display the unit class ID.
Requirements
On	CheckBox	This enables the unit. If this box is not checked, then the material will pass straight through the mill with no change to the size distribution.
Method	Fixed Discharge	The discharge particle size distribution is user defined. Different distributions can be used for different solids.
	AG/SAG (Variable Rates)	The Variable Rates AG/SAG mill model is used to determine the mill product size distribution. Different parameters can be used for different solids.
	Rod Mill (Lynch)	The Lynch rod mill model is used to determine the mill product size distribution. Different parameters can be used for different solids.
	Ball (Perfect Mixing)	The Perfect Mixing ball mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids.
	Stirred (Perfect Mixing)	The Perfect Mixing stirred mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids.
	Mill (Herbst-Fuerstenau)	The Herbst-Fuerstenau model is used to determine the mill product size distribution. Different parameters can be used for different solids.
PowerModels	CheckBox	Show alternative mill power model calculations on the Power page.
MediaTrajectory	CheckBox	Show mill media rolling, sliding and free flight trajectory computations on the MediaTraj page.
OverfillingIndicator	CheckBox	Show overflow ball mill slurry volume, residence time, and overfilling evaluation on Overfilling page.
MediaStrings	CheckBox	Show media size distributions at recharge equilibrium on the MediaStrings page.
Options
ShowQFeed	CheckBox	QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream.
ShowQProd	CheckBox	QProd and associated tab pages (eg Sp) will become visible, showing the properties of the products.
SizeForPassingFracCalc	Input	Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section.
FracForPassingSizeCalc	Input	Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section.
Stream Summary
MassFlow / Qm	Display	The total mass flow in each stream.
SolidMassFlow / SQm	Display	The Solids mass flow in each stream.
LiquidMassFlow / LQm	Display	The Liquid mass flow in each stream.
VolFlow / Qv	Display	The total Volume flow in each stream.
Temperature / T	Display	The Temperature of each stream.
Density / Rho	Display	The Density of each stream.
SolidFrac / Sf	Display	The Solid Fraction in each stream.
LiquidFrac / Lf	Display	The Liquid Fraction in each stream.
Passing	Display	The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream.
Passes	Display	The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction.

Mill page

The Mill page is used to specify the input parameters for the mill model.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
PerfectMixing
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
Requirements
NumParallelUnits	Input	The number of parallel, identical units to simulate: Feed is divided by the number of parallel units before being sent to the unit model. Unit model product is multiplied back by the same value and returned to the SysCAD product stream. All unit model result values are shown per parallel unit.
Mode	Steady State	The steady-state Perfect Mixing ball mill model is used in SysCAD Dynamic simulation mode used instead of the dynamic Perfect Mixing model described here. This approach may be useful when very large SysCAD step sizes are used and steady-state operation can be assumed between each time step.
	Dynamic	The dynamic Perfect Mixing ball mill model described here is used to determine the mill product size distribution. Different parameters can be used for different solids.
MinSubSteps	Input	The user-specified minimum number of internal models steps taken per SysCAD step.
SubSteps	Display	The actual number of internal models steps taken per SysCAD step. May be affected by breakage/discharge rates or the user-specified MinSubSteps parameter.
DischargeType	Grate	The ball mill is configured with a grate discharge.
	Overflow	The ball mill is configured with an overflow discharge. The maximum slurry volume in the mill before overflowing the trunnion is calculated by the model.
	Overflow (User)	The ball mill is configured with an overflow discharge. The user specifies the maximum slurry volume before overflow.
MediaStringsP50	CheckBox	Only visible if the MediaStrings option is checked. Replaces the BallSize.Sim user defined value with the MediaSize (All) value from the MediaStrings page. The value of BallSize.Orig should be determined on the same basis for correct scaling of a changed media charge.
Ball
Diameter	Input	The inside liner diameter of the original and simulated ball mills.
BellyLength	Input	The inside liner belly length of the simulated ball mill, excluding cones.
ConeAngle	Input	Angle of the feed and discharge end cones, measured as positive displacement from the vertical direction.
TrunnionDiameter	Input	The inside liner trunnion diameter of the simulated ball mill.
LoadFrac	Input	The volumetric load fraction of the original and simulated ball mills.
FracCS	Input	The fraction critical speed of the original and simulated ball mills.
WorkIndex	Input	Bond Ball Work Index of ore in the original mill.
BallSize	Input	Characteristic diameter of balls in original and simulated ball mills.
MaxBreakageRateFactor / K	Input	Parameter relating ball size and the size at which the breakage rate per discharge rate is maximum.
RFunction
NumSplineKnots	Input	Number of spline knots for the $R_{i}$ function.
Size	Input	Spline knot size positions.
Ln(R)	Input	Values of $\ln R$ at each spline knot position.
Power
BallVolume	Input	Volumetric fraction of mill occupied by balls and voids.
VoidFillFraction	Input	Volumetric fraction of void space between balls occupied by slurry.
BallSG	Input	Specific Gravity or density of ball media.
Results
MillVolume	Display	Volume inside mill, including cones.
MillSpeed	Display	Rotational speed of simulated mill.

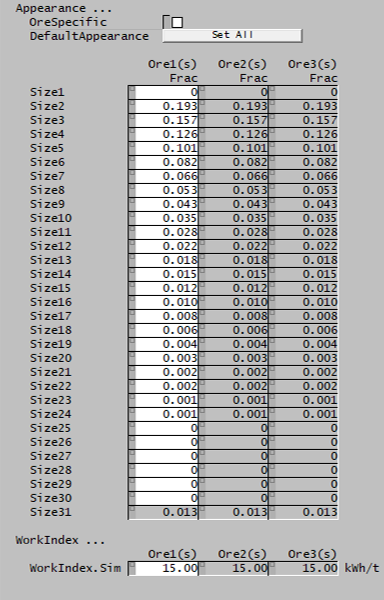
Ore page

This page is used to define the comminution properties of SysCAD species with the size distribution quality in the project.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Appearance
DefaultAppearance		Sets all species to the the default Broadbent-Callcott Appearance function.
OreSpecific	CheckBox	Ore-specific parameters, allows the Appearance data to be separately input for all species. Default is all species have the same set of single input properties. This option is only available if there is more than one species in the project with the size distribution property.
Appearance	Input	User-specified Appearance function data for all species with size distribution property.
WorkIndex
WorkIndex.Sim	Input	Bond Ball Work Index data for all species with size distribution property.

RiDi page

This page displays the scaling factors and breakage rate per discharge rate for each size interval computed by the Perfect Mixing model.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Scaling
Diameter	Display	Value of the mill diameter factor for rate scaling.
LoadFraction	Display	Value of the load fraction factor for rate scaling.
FracCS	Display	Value of the fraction critical speed factor for rate scaling.
WorkIndex	Display	Value of the Work Index factor of each ore species for rate scaling.
Rates
Size	Display	Size of each interval in internal mesh series.
MeanSize	Display	Geometric mean size of each interval in internal mesh series.
R	Display	Value of breakage rate, $R_{i}$, for each size interval, for each ore species.
C	Display	Value of classification function, $C_{i}$, for each size interval.
D	Display	Value of discharge rate, $D_{i}$, for each size interval.

Load page

This page displays information about the balls, solids and liquids that currently comprise the mill load.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Filling
SLCapacity / SLVtCap	Input / Display	The maximum volume of slurry the mill can contain before overflow.
SLCharge / SLVtCharge	Display	Only appears if DischargeType is 'Overflow'. The maximum volume of slurry that can fill the charge void space.
SLVolume / SLVt	Display	The total volume of slurry currently in the mill.
SLLevel / SLLvl	Display	The current slurry volume (SLVolume) as a fraction of the maximum slurry volume before overflow (SLCapacity).
Load
SolidMass / SMt	Display	The mass of solids with the SysCAD size distribution property currently in the mill.
LiquidMass / LMt	Display	The mass of liquids plus solids without the SysCAD size distribution property currently in the mill.
BallMass / BMt	Display	The mass of ball media in the mill.
Size	Display	Size of each interval in internal mesh series.
MeanSize	Display	Geometric mean size of each interval in internal mesh series.
Load	Display	The mass of solids with the SysCAD size distribution property currently in the mill, by size and species.

Content, Sp, Ec, Sz and MSz pages

These pages display the standard SysCAD Material Content, Species Content and Size pages for the current mill load

Power page

This optional page displays the inputs and results for alternative mill power models. The page is only visible if PowerModels is selected on the MD_Mill page.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Power
HildenPowell	CheckBox	Shows inputs and results for tumbling mill power calculations using the Hilden and Powell method.

MediaStrings page

This page displays the inputs and results for grinding mill media string calculations. The page is only visible if MediaStrings is selected on the MD_Mill page.

MediaTraj page

This page displays the inputs and results for tumbling mill media trajectory calculations. The page is only visible if MediaTrajectory is selected on the MD_Mill page.

Overfilling page

This page displays the inputs and results for overflow discharge mill overfilling calculations. The page is only visible if OverfillingIndicator is selected on the MD_Mill page.

About page

This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
About
HelpLink		Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required.
Information		Copies Product and License information to the Windows clipboard.
Product
Name	Display	Met Dynamics software product name
Version	Display	Met Dynamics software product version number.
BuildDate	Display	Build date and time of the Met Dynamics Models SysCAD Add-On.
License
File		This is used to locate a Met Dynamics software license file.
Location	Display	Type of Met Dynamics software license or file name and path of license file.
SiteCode	Display	Unique machine identifier for license authorisation.
ReqdAuth	Display	Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime.
Status	Display	License status, LICENSE_OK indicates a valid license, other messages report licensing errors.
IssuedTo	Display	Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to.
ExpiryDate	Display	Only visible if Met Dynamics license file is used. License expiry date.
DaysLeft	Display	Only visible if Met Dynamics license file is used. Days left before the license expires.

See also

• Steady-state Perfect Mixing ball mill model
• Herbst-Fuerstenau mill model