Mill (Herbst-Fuerstenau)

Description

This article describes an implementation of the Herbst and Fuerstenau (1980) grinding model.

This model is useful for simulating batch, ball, rod and stirred mill configurations, and is a grinding power-based alternative to the (otherwise very similar) Perfect Mixing model approach.

The model is particularly flexible and offers a number of different equation options for representing the parameters of grinding.

Model theory

The Herbst-Fuerstenau model is based on a population balance of particles entering the mill, breaking into smaller sizes, and discharging as product. For a mill operating in steady-state, the diagram in Figure 1 below represents the balance for a given size fraction:

Figure 1. Schematic diagram of the steady-state population balance adopted by the Herbst-Fuerstenau model.

The steady-state Herbst-Fuerstenau population balance is formulated mathematically as:

$f_{i}+\sum _{j=1}^{i-1}{b_{ij}S_{j}\tau p_{j}}-S_{i}\tau p_{i}-p_{i}=0$

which may be rearranged to yield the mill product in terms of the mill feed and breakage parameters:

$p_{i}={\dfrac {f_{i}+\sum _{j=1}^{i-1}{b_{ij}S_{j}\tau }}{1+S_{i}\tau }}$

where:

• $i$ is the index of the size interval, $i=\{1,2,\dots ,n\}$, $n$ is the number of size intervals
• $f_{i}$ is the mass fraction of particles in size interval $i$ appearing in the mill feed (w/w)
• $p_{i}$ is the mass fraction of particles in size interval $i$ appearing in the mill product (w/w)
• $S_{i}$ is the selection function at size interval $i$
• $b_{ij}$ is the breakage function, the mass fraction of a broken particle of original size $j$ appearing in size $i$ (w/w)
• $\tau$ is the mean residence time of solids in the mill $i$ (s)

The product of the selection function and mean residence time, $S_{i}\tau$, was found to be related to the energy input to grinding by:

$S_{i}\tau =S_{i}^{\rm {E}}\left({\frac {P}{W}}\right)=S_{i}^{\rm {E}}{\bar {E}}$

where:

• $S_{i}^{\rm {E}}$ is the energy-specific selection function at size interval $i$
• $P$ is the power drawn by the mill (excluding no-load power) (kW)
• $W$ is the mass flow rate of solids through the mill at steady-state (t/h)
• ${\bar {E}}$ is the specific energy input to the mill (kWh/t)

The steady-state population balance model is formulated in matrix form for steady-state continuous grinding as:

$p=TJT^{-1}f$

where:

• $f$ is a vector of the mass fractions of particles in the mill feed (w/w), $f=\{f_{i}\mid i=1,2,\dots ,n\}$
• $p$ is a vector of the mass fractions of particles in the mill product (w/w), $p=\{p_{i}\mid i=1,2,\dots ,n\}$
• $T$ and $J$ are $n$ x $n$ dimensional matrices with coefficients determined by the selection ($S_{i}^{E}$) and breakage ($b_{ij}$) functions

The matrix $T$ is defined as:

$T_{ij}={\begin{cases}0&i<j\\\\1&i=j\\\\\sum \limits _{k=j}^{i-1}{\dfrac {b_{ik}S_{k}^{\rm {E}}}{S_{i}^{\rm {E}}-S_{j}^{\rm {E}}}}T_{kj}&i>j\\\end{cases}}$

The matrix $J$ is different for batch, plug flow or continuous grinding"

$J_{ij}={\begin{cases}{\rm {e}}^{-S_{i}{\bar {E}}}&{\text{for batch or plug flow grinding when }}i=j\\\\{\dfrac {1}{\left(1+{\dfrac {S_{i}^{\rm {E}}{\bar {E}}}{N}}\right)^{N}}}&{\text{for continuous grinding when }}i=j\\\\0&i\neq j\\\end{cases}}$

where $N$ is the number of mixers-in-series approximating the residence time distribution.

Different relations are available for specifying the form of the energy-specific selection ($S_{i}^{\rm {E}}$) and breakage ($b_{ij}$) functions, which are described below.

Energy-specific selection function

The following options are available for specifying the energy-specific selection function:

• Herbst and Fuerstenau
• Austin
• User defined

Herbst and Fuerstenau

The energy-specific selection function associated with the Herbst and Fuerstenau model is:

$S_{i}^{\rm {E}}=S_{1}^{\rm {E}}\exp \left(\zeta _{1}\ln {\left({\dfrac {{\bar {d}}_{i}}{d_{{\rm {p}}1}}}\right)}+\zeta _{2}\left[\ln {\left({\dfrac {{\bar {d}}_{i}}{d_{{\rm {p}}1}}}\right)}\right]^{2}\right)$

where:

• $S_{1}^{\rm {E}}$ is the value of the energy-specific selection function ($S_{i}^{\rm {E}}$) at a nominal reference particle size ${\bar {d}}_{{\rm {p}}1}$ (mm)
• ${\bar {d}}_{i}$ is the geometric mean size of particles in size interval $i$ (mm)
• $\zeta _{1}$ and $\zeta _{2}$ are coefficients that characterise the shape of the energy-specific selection function curve

King (2012) notes the value of $d_{{\rm {p}}1}$ is often taken as the top size of the mesh series in use, although a nominal size of 1mm may also be an adequate choice.

Austin

An expanded form of the Austin selection function is available:

$S_{i}^{\rm {E}}=\left({\dfrac {1}{1+{\dfrac {\alpha _{2}}{\alpha _{1}}}}}\right)\left({\dfrac {\alpha _{0}{\bar {d_{i}}}^{\alpha _{1}}}{1+\left({\dfrac {{\bar {d}}_{i}}{d_{\rm {crit}}}}\right)^{\alpha _{2}}}}+\alpha _{02}{\bar {d_{i}}}^{\alpha _{12}}\right)$

where $\alpha _{0}$, $\alpha _{1}$, $\alpha _{2}$,$\alpha _{02}$, $\alpha _{12}$ and $d_{\rm {crit}}$ are coefficients that determine the shape of the energy-specific selection function curve.

The expanded function reduces to the standard Austin formulation when $\alpha _{02}$ is set to zero.

User defined

The user may specify the values of the energy-specific selection function at every size interval.

This may assist in the application of additional functional forms or the analysis of experimental data.

Breakage function

The following options are available for specifying the breakage function:

• Austin and Luckie
• King
• Natural selection
• User defined

Austin and Luckie

The Austin and Luckie (1972) equation for the non-normalised cumulative breakage function is:

$B_{ij}=\beta _{0j}\left({\dfrac {d_{i}}{d_{j+1}}}\right)^{\beta _{1}}+(1-\beta _{0j})\left({\dfrac {d_{i}}{d_{j+1}}}\right)^{\beta _{2}}$

where:

$\beta _{0j}=\beta _{0}{{\bar {d}}_{i}}^{-\beta _{01}}$

and:

• $B_{ij}$ is the cumulative breakage function, i.e. $b_{ij}=B_{ij}-B_{i+1,j}$
• $\beta _{0}$, $\beta _{1}$, $\beta _{2}$, $\beta _{0j}$ and $\beta _{01}$ are coefficients that determine the shape of the cumulative breakage function curve

The Austin and Luckie equation reduces to a normalised breakage function when $\beta _{01}$ is set to zero.

King

King's equation for the non-normalised cumulative breakage function is is:

$B_{ij}={\begin{cases}K\left({\dfrac {d_{i}}{y_{0}}}\right)^{n_{3}}\left({\dfrac {d_{i}}{d_{j}}}\right)^{n_{1}}+(1-K)\left({\dfrac {d_{i}}{d_{j}}}\right)^{n_{2}}&d_{i}<y_{0}\\\\K\left({\dfrac {d_{i}}{d_{j}}}\right)^{n_{1}}+(1-K)\left({\dfrac {d_{i}}{d_{j}}}\right)^{n_{2}}&d_{i}\geq y_{0}\\\end{cases}}$

where $K$, $n_{1}$, $n_{2}$ and $n_{3}$ are coefficients that determine the shape of the cumulative breakage function curve, and $y_{0}$ is the reference parent particle size (usually assumed as 5 mm).

The King equation reduces to a normalised breakage function when $y_{0}$ is set to zero.

Natural selection

Vien (2019) proposed the natural selection function, where the breakage function is dependent on the selection function:

$B_{ij}={\dfrac {S_{i}^{\rm {E}}}{S_{j}^{\rm {E}}}}\implies b_{ij}={\dfrac {S_{i-1}^{\rm {E}}-S_{i}^{\rm {E}}}{S_{j}^{\rm {E}}}}$

The natural selection function therefore eliminates a number of parameters from the Herbst-Fuerstenau model formulation.

User defined

The user may specify the values of the breakage function at every parent and progeny particle size interval.

This may assist in the application of additional functional forms or the analysis of experimental data, particularly where the breakage function is non-normalisable.

Additional notes

Parameters of the Herbst-Fuerstenau model may be adjusted to simulate batch laboratory mills, and continuous rod, ball and stirred mills.

Laboratory mills are typically operated in batch mode. They may be simulated by applying the batch form of the population balance equations (above) and reformulating ${\bar {E}}$ as:

${\bar {E}}={\dfrac {P.t}{M}}$

where $t$ is the batch grinding time (s) and $M$ is the total mass of solids in the batch.

Rod mills are often assumed to operate as plug flow devices and may also be simulated by applying the batch form of the population balance equations (above). No reformulation of ${\bar {E}}$ is required in this case.

Ball mills and stirred mills are frequently assumed to be well-mixed and may be simulated by applying the continuous form of the population balance equations and specifying the number of mixers-in-series, $N$, where appropriate.

Excel

The Herbst-Fuerstenau mill model may be invoked from the Excel formula bar with the following function call:

=mdUnit_Mill_HerbstFuerstenau(Parameters as Range, Size as Range, MillFeed as Range, Selection as Range, Breakage as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

Inputs

The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row ($i$) x column ($j$) format:

$Parameters={\begin{bmatrix}{\text{ Mixing method}}\\{\text{ Selection function method}}\\{\text{ Breakage function method}}\\P{\text{ (kW)}}\\N\end{bmatrix}},\;\;\;\;\;\;Size={\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{n}{\text{ (mm)}}\\\end{bmatrix}},\;\;\;\;\;\;MillFeed={\begin{bmatrix}(Q_{\rm {M,F}})_{11}{\text{ (t/h)}}&\dots &(Q_{\rm {M,F}})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{\rm {M,F}})_{n1}{\text{ (t/h)}}&\dots &(Q_{\rm {M,F}})_{nm}{\text{ (t/h)}}\\\end{bmatrix}}$

$Selection={\begin{cases}{\begin{bmatrix}{\begin{bmatrix}S_{1}^{\rm {E}}\\\vdots \\S_{n}^{\rm {E}}\\\end{bmatrix}}_{1}\dots {\begin{bmatrix}S_{1}^{\rm {E}}\\\vdots \\S_{n}^{\rm {E}}\\\end{bmatrix}}_{m}\end{bmatrix}}&{\text{ Selection function method}}=0{\text{ (User defined)}}\\&&\\{\begin{bmatrix}{\begin{bmatrix}S_{1}^{\rm {E}}\\\zeta _{1}\\\zeta _{2}\\d_{{\rm {p}}1}{\text{ (mm)}}\\\end{bmatrix}}_{1}\dots {\begin{bmatrix}S_{1}^{\rm {E}}\\\zeta _{1}\\\zeta _{2}\\d_{{\rm {p}}1}{\text{ (mm)}}\\\end{bmatrix}}_{m}\end{bmatrix}}&{\text{ Selection function method}}=1{\text{ (Herbst-Fuerstenau)}}\\&&\\{\begin{bmatrix}{\begin{bmatrix}\alpha _{0}\\\alpha _{1}\\\alpha _{2}\\d_{\rm {crit}}{\text{ (mm)}}\\\alpha _{02}\\\alpha _{12}\\\end{bmatrix}}_{1}\dots {\begin{bmatrix}\alpha _{0}\\\alpha _{1}\\\alpha _{2}\\d_{\rm {crit}}{\text{ (mm)}}\\\alpha _{02}\\\alpha _{12}\\\end{bmatrix}}_{m}\end{bmatrix}}&{\text{ Selection function method}}=2{\text{ (Austin)}}\\\end{cases}}$

$Breakage={\begin{cases}{\begin{bmatrix}{\begin{bmatrix}b_{11}&&0\\\vdots &\ddots &\\b_{n1}&\dots &b_{nn}\\\end{bmatrix}}_{1}\\\vdots \\{\begin{bmatrix}b_{11}&&0\\\vdots &\ddots &\\b_{n1}&\dots &b_{nn}\\\end{bmatrix}}_{m}\\\end{bmatrix}}&{\text{ Breakage function method}}=0{\text{ (User defined)}}\\&&\\{\begin{bmatrix}{\begin{bmatrix}\beta _{0}\\\beta _{1}\\\beta _{2}\\\beta _{02}\\\end{bmatrix}}_{1}\dots {\begin{bmatrix}\beta _{0}\\\beta _{1}\\\beta _{2}\\\beta _{02}\\\end{bmatrix}}_{m}\end{bmatrix}}&{\text{ Breakage function method}}=1{\text{ (Austin and Luckie)}}\\&&\\{\begin{bmatrix}{\begin{bmatrix}K\\n_{1}\\n_{2}\\n_{3}\\y_{0}{\text{ (mm)}}\\\end{bmatrix}}_{1}\dots {\begin{bmatrix}K\\n_{1}\\n_{2}\\n_{3}\\y_{0}{\text{ (mm)}}\\\end{bmatrix}}_{m}\end{bmatrix}}&{\text{ Breakage function method}}=2{\text{ (King)}}\\&&\\{\bigg [}\;\;\;{\bigg ]}&{\text{ Breakage function method}}=3{\text{ (Natural selection)}}\\\end{cases}}$

where:

• ${\text{Mixing method}}$ is the population balance equation form, 0 = Batch/Plug Flow, 1 = Continuous
• ${\text{Selection method}}$ is the selection function method, 0 = User, 1 = Herbst-Fuerstenau, 2 = Austin
• ${\text{Breakage method}}$ is the breakage function method, 0 = User, 1 = Austin & Luckie, 2 = King, 3 = Natural selection
• $m$ is the number of ore types
• $Q_{\rm {M,F}}$ is feed solids mass flow rate by size and ore type (t/h)

Results

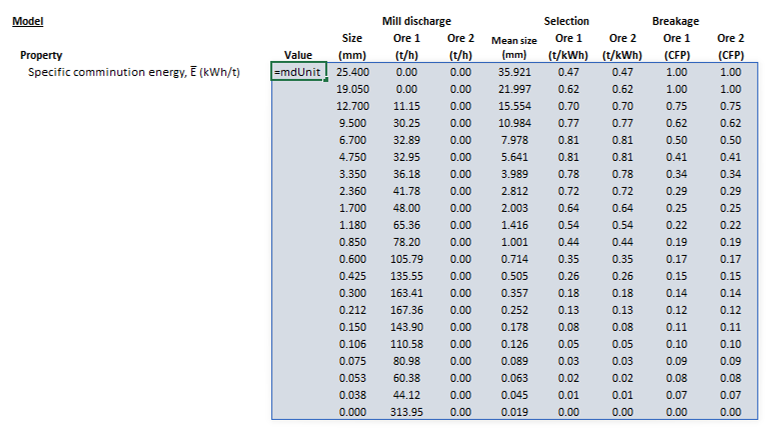
The results are displayed in Excel as an array corresponding to the matrix notation below:

$mdUnit\_Mill\_HerbstFuerstenau={\begin{bmatrix}{\begin{array}{c}{\begin{bmatrix}{\bar {E}}{\text{ (kWh/t)}}\\\end{bmatrix}}\\\\\\\end{array}}&{\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{n}{\text{ (mm)}}\end{bmatrix}}&{\begin{bmatrix}(Q_{\rm {M,P}})_{11}{\text{ (t/h)}}&\dots &(Q_{\rm {M,P}})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{\rm {M,P}})_{n1}{\text{ (t/h)}}&\dots &(Q_{\rm {M,P}})_{nm}{\text{ (t/h)}}\\\end{bmatrix}}&{\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{n}{\text{ (mm)}}\\\end{bmatrix}}&{\begin{bmatrix}{\begin{bmatrix}S_{1}^{\rm {E}}\\\vdots \\S_{n}^{\rm {E}}\\\end{bmatrix}}_{1}\dots {\begin{bmatrix}S_{1}^{\rm {E}}\\\vdots \\S_{n}^{\rm {E}}\\\end{bmatrix}}_{m}\end{bmatrix}}&{\begin{bmatrix}{\begin{bmatrix}B_{1,2}\\\vdots \\B_{n,2}\\\end{bmatrix}}_{1}\dots {\begin{bmatrix}B_{1,2}\\\vdots \\B_{n,2}\\\end{bmatrix}}_{m}\end{bmatrix}}\end{bmatrix}}$

where $Q_{\rm {M,P}}$ is product mass flow rate (t/h).

Example

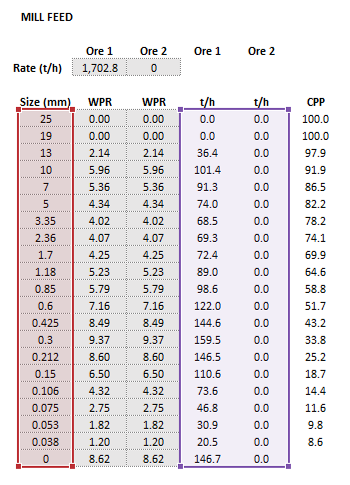
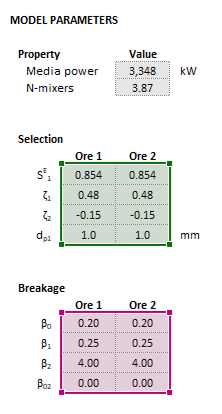
The images below show the selection of input arrays and output results in the Excel interface.

Figure 1. Example showing the selection of the Parameters (blue frame) array in Excel.

Figure 2. Example showing the selection of the Size (red frame) and MillFeed (purple frame) arrays in Excel.

Figure 3. Example showing the selection of the Selection (green frame) and Breakage (pink frame) arrays in Excel.

Figure 4. Example showing the outline of the Results (light blue frame) array in Excel.

SysCAD

The sections and variable names used in the SysCAD interface are described in detail in the following tables.

MD_Mill page

The first tab page in the access window will have this name.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Tag	Display	This name tag may be modified with the change tag option.
Condition	Display	OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount	Display	The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc	Display	This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here. If this field is blank, then SysCAD will display the unit class ID.
Requirements
On	CheckBox	This enables the unit. If this box is not checked, then the material will pass straight through the mill with no change to the size distribution.
Method	Fixed Discharge	The discharge particle size distribution is user defined. Different distributions can be used for different solids.
	AG/SAG (Variable Rates)	The Variable Rates AG/SAG mill model is used to determine the mill product size distribution. Different parameters can be used for different solids.
	Rod Mill (Lynch)	The Lynch rod mill model is used to determine the mill product size distribution. Different parameters can be used for different solids.
	Ball (Perfect Mixing)	The Perfect Mixing ball mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids.
	Stirred (Perfect Mixing)	The Perfect Mixing stirred mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids.
	Mill (Herbst-Fuerstenau)	The Herbst-Fuerstenau model is used to determine the mill product size distribution. Different parameters can be used for different solids.
PowerModels	CheckBox	Show alternative mill power model calculations on the Power page.
MediaTrajectory	CheckBox	Show mill media rolling, sliding and free flight trajectory computations on the MediaTraj page.
OverfillingIndicator	CheckBox	Show overflow ball mill slurry volume, residence time, and overfilling evaluation on Overfilling page.
MediaStrings	CheckBox	Show media size distributions at recharge equilibrium on the MediaStrings page.
Options
ShowQFeed	CheckBox	QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream.
ShowQProd	CheckBox	QProd and associated tab pages (eg Sp) will become visible, showing the properties of the products.
SizeForPassingFracCalc	Input	Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section.
FracForPassingSizeCalc	Input	Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section.
Stream Summary
MassFlow / Qm	Display	The total mass flow in each stream.
SolidMassFlow / SQm	Display	The Solids mass flow in each stream.
LiquidMassFlow / LQm	Display	The Liquid mass flow in each stream.
VolFlow / Qv	Display	The total Volume flow in each stream.
Temperature / T	Display	The Temperature of each stream.
Density / Rho	Display	The Density of each stream.
SolidFrac / Sf	Display	The Solid Fraction in each stream.
LiquidFrac / Lf	Display	The Liquid Fraction in each stream.
Passing	Display	The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream.
Passes	Display	The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction.

Mill page

The Mill page is used to specify the input parameters for the mill model.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
HerbstFuerstenau
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
Requirements
NumParallelUnits	Input	The number of parallel, identical units to simulate: Feed is divided by the number of parallel units before being sent to the unit model. Unit model product is multiplied back by the same value and returned to the SysCAD product stream. All unit model result values are shown per parallel unit.
Power
Method	User	The user specifies the power input to grinding.
	HoggFuerstenau	The power input to grinding is the Hogg and Fuerstenau model BallsPower value.
	MorrellE (Grate)	The power input to grinding is the Morrell Empirical model NetPower.Grate value.
	MorrellE (Overflow)	The power input to grinding is the Morrell Empirical model NetPower.Overflow value.
	MorrellC	The power input to grinding is the Morrell Continuum model NetPower value.
	MorrellD	The power input to grinding is the Morrell Discrete Shell model NetPower value.
	HildenPowell	The power input to grinding is the Hilden and Powell model NetPower value.
MediaPower	Input/Display	Power input to grinding. The value may be user specified or linked to the selected power model on the Power page.
Mixing
NMixers	Input	The number of mixers-in-series for grinding simulation.
Selection
Method	User	The user specifies the selection function.
	Herbst and Fuerstenau	The Herbst and Fuerstenau selection function is used.
	Austin	The Austin selection function is used.
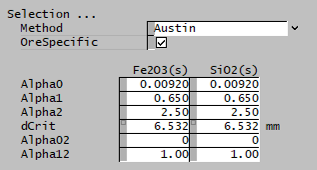
OreSpecific	CheckBox	Ore-specific parameters, allows the selection function to be separately input for all species. Default is all species have the same set of single input properties. This option is only available if there is more than one species in the project with the size distribution property.
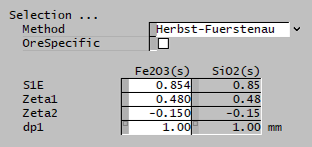
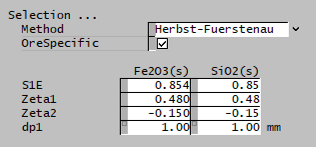
The fields below are only visible if Herbst-Fuerstenau is selected.
S1E	Input	Input parameter of the Herbst-Fuerstenau selection function.
Zeta1	Input	Input parameter of the Herbst-Fuerstenau selection function.
Zeta2	Input	Input parameter of the Herbst-Fuerstenau selection function.
dp1	Input	Input parameter of the Herbst-Fuerstenau selection function.
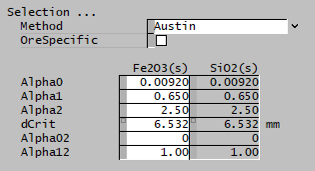
The fields below are only visible if Austin is selected.
Alpha0	Input	Input parameter of the Austin selection function.
Alpha1	Input	Input parameter of the Austin selection function.
Alpha2	Input	Input parameter of the Austin selection function.
dCrit	Input	Input parameter of the Austin selection function.
Alpha02	Input	Input parameter of the Austin selection function.
Alpha12	Input	Input parameter of the Austin selection function.
Breakage
Method	User	The user specifies the breakage function.
	Austin and Luckie	The Austin and Luckie breakage function is used.
	King	The King selection function is used.
	Natural Selection	The Natural selection function is used.
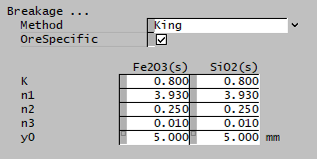
OreSpecific	CheckBox	Ore-specific parameters, allows the breakage function to be separately input for all species. Default is all species have the same set of single input properties. This option is only available if there is more than one species in the project with the size distribution property.
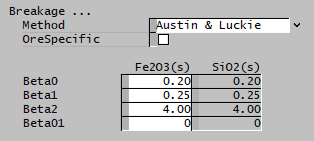
The fields below are only visible if Austin and Luckie is selected.
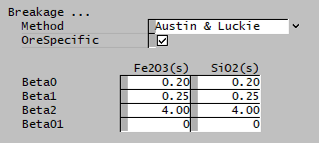
Beta0	Input	Input parameter of the Austin and Luckie breakage function.
Beta1	Input	Input parameter of the Austin and Luckie breakage function.
Beta2	Input	Input parameter of the Austin and Luckie breakage function.
Beta01	Input	Input parameter of the Austin and Luckie breakage function.
The fields below are only visible if King is selected.
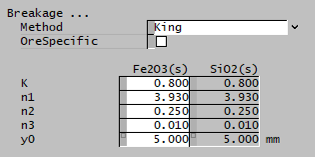
K	Input	Input parameter of the King breakage function.
n1	Input	Input parameter of the King breakage function.
n2	Input	Input parameter of the King breakage function.
n3	Input	Input parameter of the King breakage function.
y0	Input	Input parameter of the King breakage function.
Results
Ebar	Display	Specific energy of grinding.

Selection page

The Selection page is used to specify or display the selection function values.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Distribution
Name	Display	Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream.
IntervalCount	Display	Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream.
SpWithPSDCount	Display	Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality.
Selection
Size	Display	Size of each interval in mesh series.
MeanSize	Display	Geometric mean size of each interval in mesh series.
Selection	Input/Display	Value of the selection function for each size interval, for each ore species.

Breakage page

The Breakage page is used to specify or display the breakage function values.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Distribution
Name	Display	Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream.
IntervalCount	Display	Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream.
SpWithPSDCount	Display	Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality.
Breakage
Size	Display	Size of each interval in internal mesh series.
Breakage	Input/Display	Value of the breakage function for each parent size interval, progeny size interval and ore species.

Power page

This optional page displays the inputs and results for alternative mill power models. The page is only visible if PowerModels is selected on the MD_Mill page.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Power
HoggFuerstenau	CheckBox	Shows inputs and results for tumbling mill power calculations using the Hogg and Fuerstenau method.
MorrellC	CheckBox	Shows inputs and results for tumbling mill power calculations using the Morrell Continuum method.
MorrellE	CheckBox	Shows inputs and results for tumbling mill power calculations using the Morrell Empirical method.
MorrellD	CheckBox	Shows inputs and results for tumbling mill power calculations using the Morrell Discrete Shell method.
HildenPowell	CheckBox	Shows inputs and results for tumbling mill power calculations using the Hilden and Powell method.
Nitta	CheckBox	Shows inputs and results for stirred mill power calculations using the Nitta method.
Heath	CheckBox	Shows inputs and results for stirred mill power calculations using the Heath method.

MediaStrings page

This page displays the inputs and results for grinding mill media string calculations. The page is only visible if MediaStrings is selected on the MD_Mill page.

MediaTraj page

This page displays the inputs and results for tumbling mill media trajectory calculations. The page is only visible if MediaTrajectory is selected on the MD_Mill page.

Overfilling page

This page displays the inputs and results for overflow discharge mill overfilling calculations. The page is only visible if OverfillingIndicator is selected on the MD_Mill page.

About page

This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
About
HelpLink		Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required.
Information		Copies Product and License information to the Windows clipboard.
Product
Name	Display	Met Dynamics software product name
Version	Display	Met Dynamics software product version number.
BuildDate	Display	Build date and time of the Met Dynamics Models SysCAD Add-On.
License
File		This is used to locate a Met Dynamics software license file.
Location	Display	Type of Met Dynamics software license or file name and path of license file.
SiteCode	Display	Unique machine identifier for license authorisation.
ReqdAuth	Display	Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime.
Status	Display	License status, LICENSE_OK indicates a valid license, other messages report licensing errors.
IssuedTo	Display	Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to.
ExpiryDate	Display	Only visible if Met Dynamics license file is used. License expiry date.
DaysLeft	Display	Only visible if Met Dynamics license file is used. Days left before the license expires.

See also

• Perfect Mixing ball mill model
• Torres HPGR model
• Campos HPGR model