Ball Mill (Perfect Mixing): Difference between revisions
Scott Munro (talk | contribs) (Page created) |
md>Scott.Munro |
||
| Line 1: | Line 1: | ||
== Description == | == Description == | ||
This | This article describes an implementation of the '''Perfect Mixing''' ball mill model outlined by Napier-Munn et al.{{Napier-Munn_et_al._(1996)}} | ||
The model described here is for steady-state simulation. For dynamic simulation, see [[Ball Mill (Perfect Mixing, Dynamic)]]. | The model described here is for '''''steady-state''''' simulation. For dynamic simulation, ''see [[Ball Mill (Perfect Mixing, Dynamic)]]''. | ||
== Model | == Model theory == | ||
The Perfect Mixing model is based on a population balance of particles entering the mill, breaking into smaller sizes, and discharging as product. For a mill operating in steady-state, the | The Perfect Mixing model is based on a population balance of particles entering the mill, breaking into smaller sizes, and discharging as product. For a mill operating in steady-state, the diagram in Figure 1 below represents the balance for a given size fraction: | ||
:::: | ::::{| | ||
| style="padding: 10px"|<gallery mode="nolines" widths=950px heights=36px> | |||
File:BallMillPerfectMixing1.png|Figure 1. Schematic diagram of the steady-state population balance adopted by the Perfect Mixing model. | |||
</gallery> | |||
|} | |||
The steady-state population balance is formulated mathematically as: | The steady-state population balance is formulated mathematically as: | ||
:<math>f_i-R_is_i+\sum_{j=1}^{i}{A_{ij}R_js_j} - | :<math>f_i-R_is_i+\sum_{j=1}^{i}{A_{ij}R_js_j} - p_i = 0</math> | ||
where: | where: | ||
* <math> | * <math>i</math> is the index of the size interval, <math>i = \{1,2,\dots,n\}</math>, <math>n</math> is the number of size intervals | ||
* <math> | * <math>f_i</math> is the mass flow rate of solids of size interval <math>i</math> in the mill feed | ||
* <math> | * <math>p_i</math> is the mass flow rate of solids of size interval <math>i</math> in the mill product | ||
* <math> | * <math>s_i</math> is the mass of solids on size interval <math>i</math> in the mill load | ||
* <math> | * <math>R_i</math> is the breakage rate of solids on size interval <math>i</math> in the mill load | ||
* <math>A_{ij}</math> is the Appearance function, the distribution of particle mass arising from the breakage of a parent particle in size interval <math>j</math> into progeny of size interval <math>i</math> | * <math>A_{ij}</math> is the Appearance function, the distribution of particle mass arising from the breakage of a parent particle in size interval <math>j</math> into progeny of size interval <math>i</math> | ||
As the mill is perfectly mixed, the product is | As the mill is perfectly mixed, the product is related to the mill contents and discharge rate as: | ||
:<math>p_i=D_is_i</math> | :<math>p_i=D_is_i</math> | ||
where <math>D_i</math> is the rate of discharge of solids in size interval <math>i</math> from the mill. | |||
: | Substitution and rearrangement of the above equations leads to: | ||
:<math>p_i=\dfrac{f_i + \sum\limits_{j=1}^{i}{A_{ij}\dfrac{R_j}{D_j}p_j}}{1+\dfrac{R_i}{D_i}}</math> | |||
:<math> | |||
and | The mill product can therefore be computed provided a feed rate, Appearance function and ''breakage rate per discharge rate'', <math>R_i/D_i</math>, is available. Alternatively, the <math>R_i/D_i</math> function can be determined from the feed rate, product rate and Appearance function. | ||
=== Discharge rate === | |||
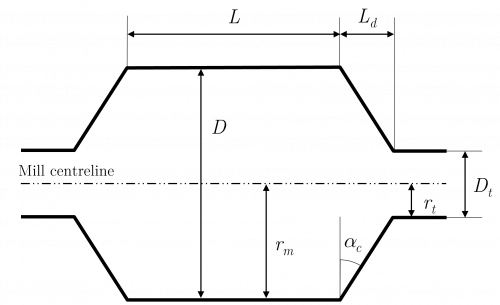
[[File:TumblingMillDimensions2.png|thumb|500px|Figure 2. Schematic of a tumbling mill showing key dimensions.]] | |||
The discharge rate, <math>D_i</math>, is related to the residence time of pulp in the mill and can be corrected for different volumetric feed rates and mill volumes by first normalising to | The discharge rate, <math>D_i</math>, is related to the residence time of pulp in the mill and can be corrected for different volumetric feed rates and mill volumes by first normalising to | ||
:<math>D_i^* = \ | :<math>D_i^* = \dfrac{D_i}{\left(\dfrac{4Q_v}{D^2L}\right)}</math> | ||
where: | where: | ||
| Line 50: | Line 51: | ||
* <math>Q_v</math> is the volumetric flow rate of pulp in mill feed (solids plus liquids) | * <math>Q_v</math> is the volumetric flow rate of pulp in mill feed (solids plus liquids) | ||
* <math>D</math> is the mill diameter (inside liners) | * <math>D</math> is the mill diameter (inside liners) | ||
* <math>L</math> is the mill length | * <math>L</math> is the mill (belly) length | ||
The actual discharge rate for a given mill and pulp feed rate is subsequently scaled as | The actual discharge rate for a given mill and pulp feed rate is subsequently scaled as | ||
:<math>D_i=D_i^* \cdot \ | :<math>D_i=D_i^* \cdot \dfrac{4Q_v}{D^2L}</math> | ||
with <math> | with <math>R_i/D_i</math> becoming <math>R_i/D_i^*</math> for mill model calibration and simulation. | ||
=== Breakage rate === | === Breakage rate === | ||
The <math> | The <math>R_i/D_i^*</math> rate is a function of particle size and is typically a smooth, concave downward curve with a maximum related to ball size. In order to reduce the number of model parameters, the rates are specified only at three or four regularly spaced sizes (''knots''). Cubic spline interpolation is then used to reconstruct the complete set of rates for all size intervals. | ||
The breakage rate, <math>R_i</math>, is affected by mill operating conditions and the <math> | The breakage rate, <math>R_i</math>, is affected by mill operating conditions and the <math>R_i/D_i^*</math> rate is further scaled by the following relation: | ||
:<math>\left(\frac{R}{D^*}\right)_{Sim} = \left(\frac{R}{D^*}\right)_{Fit} \cdot Factor_{D} \cdot Factor_{LF} \cdot Factor_{FracCS} \cdot Factor_{WI} \cdot Factor_{Db}</math> | :<math>\left(\frac{R}{D^*}\right)_{Sim} = \left(\frac{R}{D^*}\right)_{Fit} \cdot Factor_{D} \cdot Factor_{LF} \cdot Factor_{FracCS} \cdot Factor_{WI} \cdot Factor_{Db}</math> | ||
| Line 77: | Line 78: | ||
:<math> Factor_{Db} = | :<math> Factor_{Db} = | ||
\begin{cases} | |||
\begin{ | \dfrac{Db_{Orig}}{Db_{Sim}} & \text{for }x<x_{m(small)}, \;\;\;x_{m(small)}=\min{\left(K.Db_{Orig}^2, K.Db_{Sim}^2\right)}\\ | ||
\ | \left(\dfrac{Db_{Orig}}{Db_{Sim}}\right)^2 & \text{for }x\geq x_{m(large)}, \;\;\;x_{m(large)}=\max{\left(K.Db_{Orig}^2, K.Db_{Sim}^2\right)}\\ | ||
\left(\ | \end{cases} | ||
\end{ | |||
</math> | </math> | ||
where: | where: | ||
* <math>D</math> is mill diameter | * <math>D</math> is mill diameter (m) | ||
* <math>LF</math> is load fraction, the load volume as a fraction of mill volume | * <math>LF</math> is load fraction, the load volume as a fraction of mill volume (v/v) | ||
* <math>FracCS</math> is the fraction critical speed of the mill | * <math>FracCS</math> is the fraction critical speed of the mill (frac) | ||
* <math>WI</math> is the Bond | * <math>WI</math> is the Bond Ball Work Index of the ore (kWh/t) | ||
* <math>Db</math> is the ball diameter | * <math>Db</math> is the ball diameter (mm) | ||
* <math>K</math> is the maximum breakage rate factor which relates ball size and the size at which <math> | * <math>x</math> is the diameter of a particle of size interval <math>i</math> (mm) | ||
* <math>K</math> is the maximum breakage rate factor which relates ball size and the size at which <math>R_i/D_i^*</math> is maximum, i.e. <math>x_m=K.D_b^2</math> | |||
* <math>Factor_{Db}</math> is interpolated for <math>x_{m(small)}<x<x_{m(large)}</math> | |||
and the <math>Orig</math> subscript refers to the original mill from which <math> | and the <math>Orig</math> subscript refers to the original mill from which <math>R_i/D_i^*</math> was derived and <math>Sim</math> refers to the mill being simulated (scaled). | ||
The grouping of breakage rate scaling factors above, excluding work index, essentially represent a relationship with mill power draw, as noted by Napier-Munn et al., King and others. | The grouping of breakage rate scaling factors above, excluding work index, essentially represent a relationship with mill power draw, as noted by Napier-Munn et al., King and others.{{Napier-Munn_et_al. (1996)}}{{King (2012)}} | ||
=== Appearance function === | === Appearance function === | ||
| Line 101: | Line 102: | ||
The Appearance function describes the mass-by-size distribution of progeny particles resulting from the breakage of parent particles. | The Appearance function describes the mass-by-size distribution of progeny particles resulting from the breakage of parent particles. | ||
The Appearance function may be specified for a particular ore. Alternatively, the default Broadbent-Callcott appearance function may be used, which is defined as: | The Appearance function may be specified for a particular ore. Alternatively, the default Broadbent-Callcott appearance function may be used, which is defined as:{{Gupta_and_Yan_(2016)}} | ||
:<math>A_{ij}=\frac{1-\exp(-\ | :<math>A_{ij}=\frac{1-\exp \left(-\dfrac{d_i}{d_j} \right)}{1-\exp(-1)}</math> | ||
where <math>d_i</math> is the breakage product particle size and <math>d_j</math> is the original particle size. | where <math>d_i</math> is the breakage product particle size and <math>d_j</math> is the original particle size. | ||
=== Internal mesh series === | === Internal mesh series === | ||
The Perfect Mixing ball mill model is formulated internally with a geometric progression of mesh sizes at <math>\sqrt{2}</math> intervals. Feed and product size fractions are automatically converted to and from the internal mesh series during model computation. The <math>\sqrt{2}</math> size intervals allow the Appearance function to be specified as a one-dimensional matrix, rather than the two dimensional form defined above, since | The Perfect Mixing ball mill model is formulated internally with a geometric progression of 31 mesh sizes at <math>\sqrt{2}</math> intervals. Feed and product size fractions are automatically converted to and from the internal mesh series during model computation. The <math>\sqrt{2}</math> size intervals allow the Appearance function to be specified as a one-dimensional matrix, rather than the two dimensional form defined above, since | ||
:<math>A_{ij}=A_{i-j}</math> | :<math>A_{ij}=A_{i-j}</math> | ||
| Line 114: | Line 115: | ||
when the intervals are so spaced. | when the intervals are so spaced. | ||
=== | === Multi-component modelling === | ||
The | The original Perfect Mixing model formulation only considered the properties of a single ore type. | ||
This model internally applies different Appearance functions and breakage rate scaling to separate population balance computations for each ore type (mineral) in the feed, as conceptually suggested by Napier-Munn et al.<ref name="Napier-Munn_et_al._(1996)" /> | |||
=== | === Power draw === | ||
The | The Perfect Mixing mill model formulation does not explicitly include a relationship with mill power draw, other than the breakage rate scaling observations noted above. | ||
However, a simple estimate of power draw is provided for user convenience. Power is calculated according to the [[Tumbling Mill (Power, Morrell Empirical)|Morrell Empirical]] approach for grate and overflow discharge mills.{{Morrell_(1996b)}} | |||
== Excel == | == Excel == | ||
The Perfect Mixing ball mill model may be invoked from the Excel | The Perfect Mixing ball mill model may be invoked from the Excel formula bar with the following function call: | ||
<syntaxhighlight lang="vb">=mdUnit_BallMill_PerfectMixing(Parameters as Range, Size as Range, MillFeed as Range, OreSG As Range, WorkIndexSim As Range, Appearance as Range, R/D*KnotPositions as Range, R/D*KnotsOrig as Range)</syntaxhighlight> | |||
{{Excel (Text, Help, No Arguments)}} | |||
=== Inputs === | === Inputs === | ||
{{Excel (Text, Inputs)}} | |||
:<math>Parameters= | :<math>Parameters= | ||
\begin{bmatrix} | \begin{bmatrix} | ||
D_{Orig}\text{ (m)}\\ | |||
LF_{Orig}\text{ (v/v)}\\ | |||
FracCS_{Orig}\text{ (frac)}\\ | |||
WI_{Orig}\text{ (kWh/t)}\\ | |||
Db_{Orig}\text{ (mm)}\\ | |||
D_{Sim}\text{ (m)}\\ | |||
LF_{Sim}\text{ (v/v)}\\ | |||
FracCS_{Sim}\text{ (frac)}\\ | |||
WI_{Sim}\text{ (kWh/t)}\\ | |||
Db_{Sim}\text{ (mm)}\\ | |||
K\\ | |||
L\text{ (m)}\\ | |||
\alpha_{c}\text{ (deg.)}\\ | |||
D_t\text{ (m)}\\ | |||
J_B\text{ (v/v)}\\ | |||
U\text{ (v/v)}\\ | |||
Liquids | \rho_B\text{ (t/m}^{\text{3}}\text{)}\\ | ||
Q_m^{Liquids}\text{ (t/h)}\\ | |||
\rho_L\text{ (t/m}^{\text{3}}\text{)}\\ | |||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
| Line 171: | Line 169: | ||
MillFeed= \begin{bmatrix} | MillFeed= \begin{bmatrix} | ||
(Q_m^F)_{11}\text{ (t/h)} & \dots & (Q_m^F)_{1m}\text{ (t/h)}\\ | |||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
(Q_m^F)_{n1}\text{ (t/h)} & \dots & (Q_m^F)_{nm}\text{ (t/h)}\\ | |||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
| Line 182: | Line 180: | ||
:<math> | :<math> | ||
WI_{Sim}= \begin{bmatrix} | |||
WI_{1}\text{ (kWh/t)} & \dots & WI_m\text{ (kWh/t)}\\ | |||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
| Line 200: | Line 198: | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
R/D^*KnotPositions= \begin{bmatrix} | |||
d_{1}\text{ (mm)}\\ | d_{1}\text{ (mm)}\\ | ||
\vdots\\ | \vdots\\ | ||
| Line 206: | Line 204: | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
R/D^*KnotOrig= \begin{bmatrix} | |||
\ln\left(\frac{R}{D^*}\right)_1\\ | \ln\left(\frac{R}{D^*}\right)_1\\ | ||
\vdots\\ | \vdots\\ | ||
| Line 214: | Line 212: | ||
where: | where: | ||
* <math>\alpha_{c}</math> is angle between the cone end surface and the vertical direction (degrees) | |||
* <math>D_t</math> is the diameter of the discharge trunnion (m) | |||
* <math>J_B</math> is the ball charge volume fraction (often <math>J_B = LF</math>) (v/v) | |||
* <math>U</math> is the void fill fraction, the volumetric fraction of grinding media interstitial void space occupied by slurry (v/v) | |||
* <math>\rho_B</math> is the specific gravity or density of the ball media (excluding void space) (- or t/m<sup>3</sup>) | |||
* <math>Q_m^{Liquids}</math> is the mass flow feed rate of liquids into the mill (t/h) | |||
* <math>\rho_L</math> is the specific gravity or density of liquids in the feed (- or t/m<sup>3</sup>) | |||
* <math>n</math> is the number of size intervals | * <math>n</math> is the number of size intervals | ||
* <math>m</math> is the number of ore types | * <math>m</math> is the number of ore types | ||
| Line 219: | Line 224: | ||
* <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm) | * <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm) | ||
* <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm) | * <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm) | ||
* <math> | * <math>Q_m^F</math> is the mass flow rate of particles in the feed (t/h) | ||
* <math>SG</math> is Specific Gravity or density (- or t/m<sup>3</sup>) | * <math>SG</math> is the Specific Gravity or density of solids (- or t/m<sup>3</sup>) | ||
* <math>A_i</math> is the Appearance function value, the fraction of parent particle mass appearing in size interval <math>i</math> (frac) | * <math>A_i</math> is the Appearance function value, the fraction of parent particle mass appearing in internal size interval <math>i</math> (frac) | ||
* <math>\frac{R_i}{D_i^*}</math> is breakage rate per discharge rate normalised for residence time (h<sup>-1</sup>/h<sup>-1</sup>/h) | * <math>\frac{R_i}{D_i^*}</math> is breakage rate per discharge rate normalised for residence time (h<sup>-1</sup>/h<sup>-1</sup>/h) | ||
| Line 238: | Line 243: | ||
\text{Charge density (t/m}^{\text{3}}\text{)}\\ | \text{Charge density (t/m}^{\text{3}}\text{)}\\ | ||
\text{No-load power (kw)}\\ | \text{No-load power (kw)}\\ | ||
\text{Gross power (grate)}\\ | \text{Gross power (grate) (kW)}\\ | ||
\text{Gross power (overflow) (kW)}\\ | \text{Gross power (overflow) (kW)}\\ | ||
\text{R/D* factor (frac)}\\ | \text{R/D* factor (frac)}\\ | ||
\text{ | Factor_D\text{ (frac)}\\ | ||
\text{ | Factor_{LF}\text{ (frac)}\\ | ||
\text{ | Factor_{CS}\text{ (frac)}\\ | ||
xm(small)\text{ (mm)}\\ | |||
xm(large)\text{ (mm)}\\ | |||
\end{bmatrix} | \end{bmatrix} | ||
| Line 261: | Line 266: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
(Q_m^P)_{11}\text{ (t/h)} & \dots & (Q_m^P)_{1m}\text{ (t/h)}\\ | |||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
(Q_m^P)_{n1}\text{ (t/h)} & \dots & (Q_m^P)_{nm}\text{ (t/h)}\\ | |||
\end{bmatrix} | \end{bmatrix} | ||
| Line 271: | Line 276: | ||
\bar{d}_1\text{ (mm)}\\ | \bar{d}_1\text{ (mm)}\\ | ||
\vdots\\ | \vdots\\ | ||
\bar{d} | \bar{d}_{31}\text{ (mm)}\\ | ||
\end{bmatrix} | \end{bmatrix} | ||
| Line 279: | Line 284: | ||
\frac{R_i}{D_i^*}_{11}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right) & \dots & \frac{R_i}{D_i^*}_{1m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right)\\ | \frac{R_i}{D_i^*}_{11}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right) & \dots & \frac{R_i}{D_i^*}_{1m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right)\\ | ||
\vdots & \ddots & \vdots \\ | \vdots & \ddots & \vdots \\ | ||
\frac{R_i}{D_i^*}_{ | \frac{R_i}{D_i^*}_{31,1}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right) & \dots & \frac{R_i}{D_i^*}_{31m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right)\\ | ||
\end{bmatrix} | \end{bmatrix} | ||
| Line 287: | Line 292: | ||
\frac{R_i}{D_i}_{11}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right) & \dots & \frac{R_i}{D_i}_{1m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right)\\ | \frac{R_i}{D_i}_{11}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right) & \dots & \frac{R_i}{D_i}_{1m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right)\\ | ||
\vdots & \ddots & \vdots \\ | \vdots & \ddots & \vdots \\ | ||
\frac{R_i}{D_i}_{ | \frac{R_i}{D_i}_{31,1}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right) & \dots & \frac{R_i}{D_i}_{31m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right)\\ | ||
\end{bmatrix} | \end{bmatrix} | ||
| Line 311: | Line 316: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
(Factor_{WI})_1 & \dots & (Factor_{WI})_m | |||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
& & & & & &\\ | |||
& & & & & &\\ | |||
\end{array} | \end{array} | ||
| Line 319: | Line 327: | ||
</math> | </math> | ||
where: | |||
* <math>\text{Mill volumetric feed rate}</math> is the flow rate of pulp into the mill (m<sup>3</sup>/h) | |||
* <math>\text{Mill volume}</math> is the total volume inside the mill, calculated as the sum of a cylinder and two frustums (m<sup>3</sup>) | |||
* <math>\text{Mill speed}</math> is the [[Tumbling Mill (Speed)|rotational rate of the mill]] (rpm) | |||
* <math>\text{Charge density}</math> is the combined density of the charge, including grinding media, coarse ore, slurry and void space (t/m<sup>3</sup>) | |||
* <math>\text{No-load power}</math> is the power input to the motor when the mill is rotating but empty (no balls, rocks or slurry) (kW) | |||
* <math>\text{Gross power (grate)}</math> is the total power input to the motor if the mill is configured with a grate discharge (kW) | |||
* <math>\text{Gross power (overflow)}</math> is the total power input to the motor if the mill is configured with an overflow discharge (kW) | |||
* <math>\text{R/D* factor}=D_i^*/D_i</math> is the discharge rate scaling factor | |||
* <math>Q_m^P</math> is the mass flow rate of particles in the mill product (t/h) | |||
* <math>\bar{d}_i</math> is the [[Conversions|geometric mean size]] of the internal mesh series interval that mass is retained on (mm) | |||
=== Example === | === Example === | ||
| Line 327: | Line 344: | ||
{| | {| | ||
|- style="vertical-align:top;" | |- style="vertical-align:top;" | ||
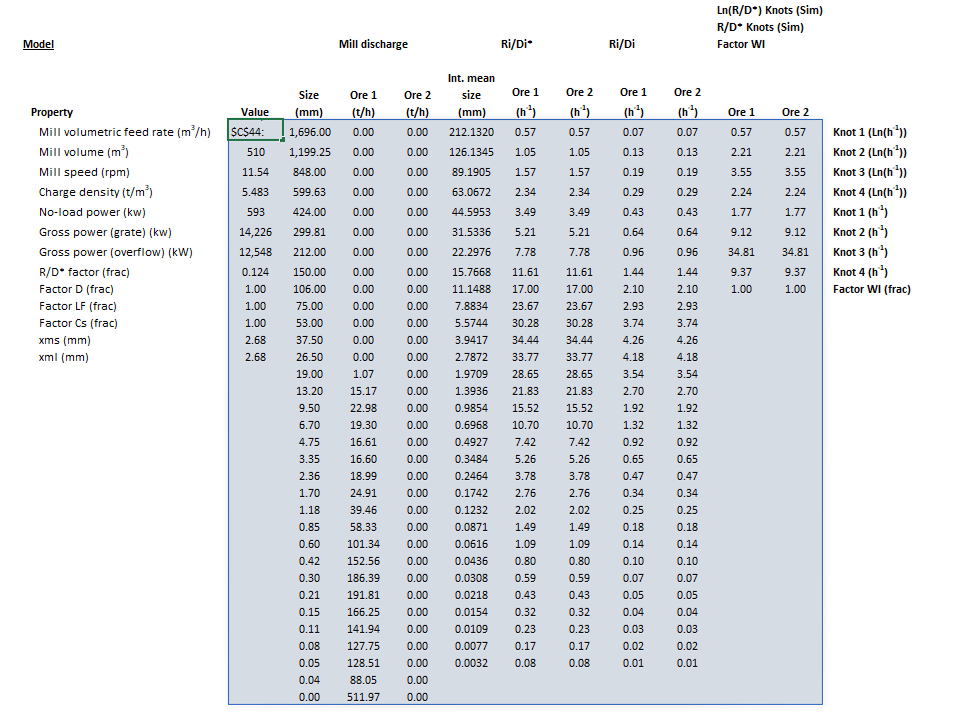
| [[File:BallMillPerfectMixing2.png|left|frame|'''Parameters''' (blue frame)]] | | [[File:BallMillPerfectMixing2.png|left|frame|Figure 3. Example showing the selection of the '''Parameters''' (blue frame) array in Excel.]] | ||
[[File:BallMillPerfectMixing5.png|left|frame|'''Results''' (light blue frame)]] | [[File:BallMillPerfectMixing5.png|left|frame|Figure 4. Example showing the outline of the '''Results''' (light blue frame) array in Excel.]] | ||
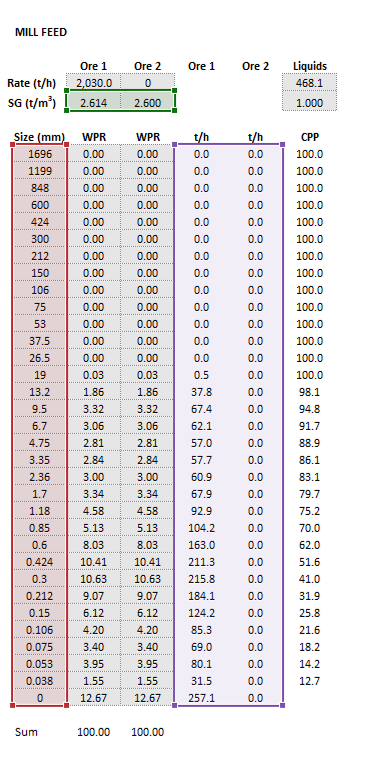
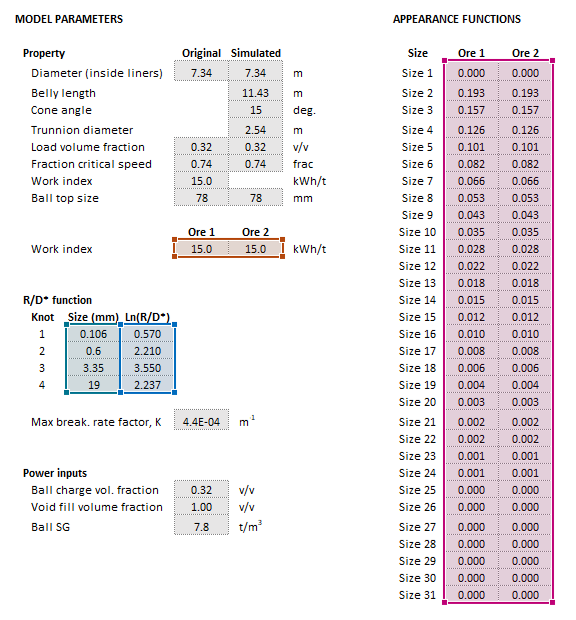
|| [[File:BallMillPerfectMixing3.png|left|frame|'''Size''' (red frame), '''OreSG''' (green frame) and '''MillFeed''' (purple frame)]] || [[File:BallMillPerfectMixing4.png|left|frame|'''Appearance''' (pink frame), '''R/D*KnotPositions''' (teal frame), '''R/D*KnotsOrig''' (blue frame), '''WorkIndexSim''' (red frame)]] | || [[File:BallMillPerfectMixing3.png|left|frame|Figure 5. Example showing the selection of the '''Size''' (red frame), '''OreSG''' (green frame) and '''MillFeed''' (purple frame).]] || [[File:BallMillPerfectMixing4.png|left|frame|Figure 6. Example showing the selection of the '''Appearance''' (pink frame), '''R/D*KnotPositions''' (teal frame), '''R/D*KnotsOrig''' (blue frame), '''WorkIndexSim''' (red frame) arrays in Excel.]] | ||
|} | |} | ||
== SysCAD == | == SysCAD == | ||
The SysCAD interface for steady-state (ProBal) mode is described below. For SysCAD Dynamic, see [[Ball Mill (Perfect Mixing, Dynamic)]] | The SysCAD interface for steady-state (ProBal) mode is described below. For SysCAD Dynamic, see ''[[Ball Mill (Perfect Mixing, Dynamic)]]''. | ||
{{SysCAD (Page, Ball Mill, ScdMD*BallMill)|method=0}} | |||
{{ | {{SysCAD (Page, Ball Mill, Perfect Mixing, Mill)|method=0}} | ||
{{ | {{SysCAD (Page, Ball Mill, Perfect Mixing, Ore)}} | ||
{{SysCAD (Page, Ball Mill, Perfect Mixing, Ri/Di)|method=0}} | |||
| | |||
== | {{SysCAD (Page, Tumbling Mill, Power)|modelpage=ScdMD*BallMill|method=0}} | ||
{{SysCAD (Page, Tumbling Mill, MediaTraj)|modelpage=ScdMD*BallMill}} | |||
{{ | {{SysCAD (Page, BallMill Overfilling)|modelpage=ScdMD*BallMill}} | ||
{{SysCAD (Page, About)}} | |||
== | == See also == | ||
* [[Ball Mill (Perfect Mixing, Dynamic)|Dynamic Perfect Mixing ball mill model]] | |||
* [[Mill (Herbst-Fuerstenau)| Herbst-Fuerstenau mill model]] | |||
| | |||
|- | |||
== References == | == References == | ||
[[Category:Excel]] | [[Category:Excel]] | ||
[[Category:SysCAD]] | [[Category:SysCAD]] | ||
Revision as of 05:02, 16 November 2022
Description
This article describes an implementation of the Perfect Mixing ball mill model outlined by Napier-Munn et al.[1]
The model described here is for steady-state simulation. For dynamic simulation, see Ball Mill (Perfect Mixing, Dynamic).
Model theory
The Perfect Mixing model is based on a population balance of particles entering the mill, breaking into smaller sizes, and discharging as product. For a mill operating in steady-state, the diagram in Figure 1 below represents the balance for a given size fraction:
The steady-state population balance is formulated mathematically as:
- [math]\displaystyle{ f_i-R_is_i+\sum_{j=1}^{i}{A_{ij}R_js_j} - p_i = 0 }[/math]
where:
- [math]\displaystyle{ i }[/math] is the index of the size interval, [math]\displaystyle{ i = \{1,2,\dots,n\} }[/math], [math]\displaystyle{ n }[/math] is the number of size intervals
- [math]\displaystyle{ f_i }[/math] is the mass flow rate of solids of size interval [math]\displaystyle{ i }[/math] in the mill feed
- [math]\displaystyle{ p_i }[/math] is the mass flow rate of solids of size interval [math]\displaystyle{ i }[/math] in the mill product
- [math]\displaystyle{ s_i }[/math] is the mass of solids on size interval [math]\displaystyle{ i }[/math] in the mill load
- [math]\displaystyle{ R_i }[/math] is the breakage rate of solids on size interval [math]\displaystyle{ i }[/math] in the mill load
- [math]\displaystyle{ A_{ij} }[/math] is the Appearance function, the distribution of particle mass arising from the breakage of a parent particle in size interval [math]\displaystyle{ j }[/math] into progeny of size interval [math]\displaystyle{ i }[/math]
As the mill is perfectly mixed, the product is related to the mill contents and discharge rate as:
- [math]\displaystyle{ p_i=D_is_i }[/math]
where [math]\displaystyle{ D_i }[/math] is the rate of discharge of solids in size interval [math]\displaystyle{ i }[/math] from the mill.
Substitution and rearrangement of the above equations leads to:
- [math]\displaystyle{ p_i=\dfrac{f_i + \sum\limits_{j=1}^{i}{A_{ij}\dfrac{R_j}{D_j}p_j}}{1+\dfrac{R_i}{D_i}} }[/math]
The mill product can therefore be computed provided a feed rate, Appearance function and breakage rate per discharge rate, [math]\displaystyle{ R_i/D_i }[/math], is available. Alternatively, the [math]\displaystyle{ R_i/D_i }[/math] function can be determined from the feed rate, product rate and Appearance function.
Discharge rate
The discharge rate, [math]\displaystyle{ D_i }[/math], is related to the residence time of pulp in the mill and can be corrected for different volumetric feed rates and mill volumes by first normalising to
- [math]\displaystyle{ D_i^* = \dfrac{D_i}{\left(\dfrac{4Q_v}{D^2L}\right)} }[/math]
where:
- [math]\displaystyle{ D_i^* }[/math] is the residence time normalised discharge rate per size interval [math]\displaystyle{ i }[/math]
- [math]\displaystyle{ Q_v }[/math] is the volumetric flow rate of pulp in mill feed (solids plus liquids)
- [math]\displaystyle{ D }[/math] is the mill diameter (inside liners)
- [math]\displaystyle{ L }[/math] is the mill (belly) length
The actual discharge rate for a given mill and pulp feed rate is subsequently scaled as
- [math]\displaystyle{ D_i=D_i^* \cdot \dfrac{4Q_v}{D^2L} }[/math]
with [math]\displaystyle{ R_i/D_i }[/math] becoming [math]\displaystyle{ R_i/D_i^* }[/math] for mill model calibration and simulation.
Breakage rate
The [math]\displaystyle{ R_i/D_i^* }[/math] rate is a function of particle size and is typically a smooth, concave downward curve with a maximum related to ball size. In order to reduce the number of model parameters, the rates are specified only at three or four regularly spaced sizes (knots). Cubic spline interpolation is then used to reconstruct the complete set of rates for all size intervals.
The breakage rate, [math]\displaystyle{ R_i }[/math], is affected by mill operating conditions and the [math]\displaystyle{ R_i/D_i^* }[/math] rate is further scaled by the following relation:
- [math]\displaystyle{ \left(\frac{R}{D^*}\right)_{Sim} = \left(\frac{R}{D^*}\right)_{Fit} \cdot Factor_{D} \cdot Factor_{LF} \cdot Factor_{FracCS} \cdot Factor_{WI} \cdot Factor_{Db} }[/math]
The scaling factors are defined as:
- [math]\displaystyle{ Factor_{D}=\sqrt{\frac{D_{Sim}}{D_{Orig}}} }[/math]
- [math]\displaystyle{ Factor_{LF}=\frac{(1-LF_{Sim}).LF_{Sim}}{(1-LF_{Orig}).LF_{Orig}} }[/math]
- [math]\displaystyle{ Factor_{FracCS}=\frac{FracCS_{Sim}}{FracCS_{Orig}} }[/math]
- [math]\displaystyle{ Factor_{WI}=\left(\frac{WI_{Orig}}{WI_{Sim}}\right)^{0.8} }[/math]
- [math]\displaystyle{ Factor_{Db} = \begin{cases} \dfrac{Db_{Orig}}{Db_{Sim}} & \text{for }x\lt x_{m(small)}, \;\;\;x_{m(small)}=\min{\left(K.Db_{Orig}^2, K.Db_{Sim}^2\right)}\\ \left(\dfrac{Db_{Orig}}{Db_{Sim}}\right)^2 & \text{for }x\geq x_{m(large)}, \;\;\;x_{m(large)}=\max{\left(K.Db_{Orig}^2, K.Db_{Sim}^2\right)}\\ \end{cases} }[/math]
where:
- [math]\displaystyle{ D }[/math] is mill diameter (m)
- [math]\displaystyle{ LF }[/math] is load fraction, the load volume as a fraction of mill volume (v/v)
- [math]\displaystyle{ FracCS }[/math] is the fraction critical speed of the mill (frac)
- [math]\displaystyle{ WI }[/math] is the Bond Ball Work Index of the ore (kWh/t)
- [math]\displaystyle{ Db }[/math] is the ball diameter (mm)
- [math]\displaystyle{ x }[/math] is the diameter of a particle of size interval [math]\displaystyle{ i }[/math] (mm)
- [math]\displaystyle{ K }[/math] is the maximum breakage rate factor which relates ball size and the size at which [math]\displaystyle{ R_i/D_i^* }[/math] is maximum, i.e. [math]\displaystyle{ x_m=K.D_b^2 }[/math]
- [math]\displaystyle{ Factor_{Db} }[/math] is interpolated for [math]\displaystyle{ x_{m(small)}\lt x\lt x_{m(large)} }[/math]
and the [math]\displaystyle{ Orig }[/math] subscript refers to the original mill from which [math]\displaystyle{ R_i/D_i^* }[/math] was derived and [math]\displaystyle{ Sim }[/math] refers to the mill being simulated (scaled).
The grouping of breakage rate scaling factors above, excluding work index, essentially represent a relationship with mill power draw, as noted by Napier-Munn et al., King and others.[1][2]
Appearance function
The Appearance function describes the mass-by-size distribution of progeny particles resulting from the breakage of parent particles.
The Appearance function may be specified for a particular ore. Alternatively, the default Broadbent-Callcott appearance function may be used, which is defined as:[3]
- [math]\displaystyle{ A_{ij}=\frac{1-\exp \left(-\dfrac{d_i}{d_j} \right)}{1-\exp(-1)} }[/math]
where [math]\displaystyle{ d_i }[/math] is the breakage product particle size and [math]\displaystyle{ d_j }[/math] is the original particle size.
Internal mesh series
The Perfect Mixing ball mill model is formulated internally with a geometric progression of 31 mesh sizes at [math]\displaystyle{ \sqrt{2} }[/math] intervals. Feed and product size fractions are automatically converted to and from the internal mesh series during model computation. The [math]\displaystyle{ \sqrt{2} }[/math] size intervals allow the Appearance function to be specified as a one-dimensional matrix, rather than the two dimensional form defined above, since
- [math]\displaystyle{ A_{ij}=A_{i-j} }[/math]
when the intervals are so spaced.
Multi-component modelling
The original Perfect Mixing model formulation only considered the properties of a single ore type.
This model internally applies different Appearance functions and breakage rate scaling to separate population balance computations for each ore type (mineral) in the feed, as conceptually suggested by Napier-Munn et al.[4]
Power draw
The Perfect Mixing mill model formulation does not explicitly include a relationship with mill power draw, other than the breakage rate scaling observations noted above.
However, a simple estimate of power draw is provided for user convenience. Power is calculated according to the Morrell Empirical approach for grate and overflow discharge mills.[5]
Excel
The Perfect Mixing ball mill model may be invoked from the Excel formula bar with the following function call:
=mdUnit_BallMill_PerfectMixing(Parameters as Range, Size as Range, MillFeed as Range, OreSG As Range, WorkIndexSim As Range, Appearance as Range, R/D*KnotPositions as Range, R/D*KnotsOrig as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row ([math]\displaystyle{ i }[/math]) x column ([math]\displaystyle{ j }[/math]) format:
- [math]\displaystyle{ Parameters= \begin{bmatrix} D_{Orig}\text{ (m)}\\ LF_{Orig}\text{ (v/v)}\\ FracCS_{Orig}\text{ (frac)}\\ WI_{Orig}\text{ (kWh/t)}\\ Db_{Orig}\text{ (mm)}\\ D_{Sim}\text{ (m)}\\ LF_{Sim}\text{ (v/v)}\\ FracCS_{Sim}\text{ (frac)}\\ WI_{Sim}\text{ (kWh/t)}\\ Db_{Sim}\text{ (mm)}\\ K\\ L\text{ (m)}\\ \alpha_{c}\text{ (deg.)}\\ D_t\text{ (m)}\\ J_B\text{ (v/v)}\\ U\text{ (v/v)}\\ \rho_B\text{ (t/m}^{\text{3}}\text{)}\\ Q_m^{Liquids}\text{ (t/h)}\\ \rho_L\text{ (t/m}^{\text{3}}\text{)}\\ \end{bmatrix},\;\;\;\;\;\; Size = \begin{bmatrix} d_{1}\text{ (mm)}\\ \vdots\\ d_n\text{ (mm)}\\ \end{bmatrix},\;\;\;\;\;\; MillFeed= \begin{bmatrix} (Q_m^F)_{11}\text{ (t/h)} & \dots & (Q_m^F)_{1m}\text{ (t/h)}\\ \vdots & \ddots & \vdots\\ (Q_m^F)_{n1}\text{ (t/h)} & \dots & (Q_m^F)_{nm}\text{ (t/h)}\\ \end{bmatrix},\;\;\;\;\;\; OreSG= \begin{bmatrix} SG_{1}\text{ (t/m}^\text{3}\text{)} & \dots & SG_m\text{ (t/m}^\text{3}\text{)}\\ \end{bmatrix} }[/math]
- [math]\displaystyle{ WI_{Sim}= \begin{bmatrix} WI_{1}\text{ (kWh/t)} & \dots & WI_m\text{ (kWh/t)}\\ \end{bmatrix},\;\;\;\;\;\; Appearance= \begin{bmatrix} \begin{bmatrix} A_{1}\text{ (frac)}\\ \vdots\\ A_{31}\text{ (frac)}\\ \end{bmatrix}_1 \dots \begin{bmatrix} A_{1}\text{ (frac)}\\ \vdots\\ A_{31}\text{ (frac)}\\ \end{bmatrix}_m \end{bmatrix},\;\;\;\;\;\; R/D^*KnotPositions= \begin{bmatrix} d_{1}\text{ (mm)}\\ \vdots\\ d_{k}\text{ (mm)}\\ \end{bmatrix},\;\;\;\;\;\; R/D^*KnotOrig= \begin{bmatrix} \ln\left(\frac{R}{D^*}\right)_1\\ \vdots\\ \ln\left(\frac{R}{D^*}\right)_k\\ \end{bmatrix} }[/math]
where:
- [math]\displaystyle{ \alpha_{c} }[/math] is angle between the cone end surface and the vertical direction (degrees)
- [math]\displaystyle{ D_t }[/math] is the diameter of the discharge trunnion (m)
- [math]\displaystyle{ J_B }[/math] is the ball charge volume fraction (often [math]\displaystyle{ J_B = LF }[/math]) (v/v)
- [math]\displaystyle{ U }[/math] is the void fill fraction, the volumetric fraction of grinding media interstitial void space occupied by slurry (v/v)
- [math]\displaystyle{ \rho_B }[/math] is the specific gravity or density of the ball media (excluding void space) (- or t/m3)
- [math]\displaystyle{ Q_m^{Liquids} }[/math] is the mass flow feed rate of liquids into the mill (t/h)
- [math]\displaystyle{ \rho_L }[/math] is the specific gravity or density of liquids in the feed (- or t/m3)
- [math]\displaystyle{ n }[/math] is the number of size intervals
- [math]\displaystyle{ m }[/math] is the number of ore types
- [math]\displaystyle{ k }[/math] is the number of breakage rate per discharge rate knots
- [math]\displaystyle{ d_i }[/math] is the size of the square mesh interval that feed mass is retained on (mm)
- [math]\displaystyle{ d_{i+1}\lt d_i\lt d_{i-1} }[/math], i.e. descending size order from top size ([math]\displaystyle{ d_{1} }[/math]) to sub mesh ([math]\displaystyle{ d_{n}=0 }[/math] mm)
- [math]\displaystyle{ Q_m^F }[/math] is the mass flow rate of particles in the feed (t/h)
- [math]\displaystyle{ SG }[/math] is the Specific Gravity or density of solids (- or t/m3)
- [math]\displaystyle{ A_i }[/math] is the Appearance function value, the fraction of parent particle mass appearing in internal size interval [math]\displaystyle{ i }[/math] (frac)
- [math]\displaystyle{ \frac{R_i}{D_i^*} }[/math] is breakage rate per discharge rate normalised for residence time (h-1/h-1/h)
Results
The results are displayed in Excel as an array corresponding to the matrix notation below:
- [math]\displaystyle{ mdUnit\_BallMill\_PerfectMixing = \begin{bmatrix} \begin{bmatrix} \text{Mill volumetric feed rate (m}^{\text{3}}\text{/h)}\\ \text{Mill volume (m}^{\text{3}}\text{)}\\ \text{Mill speed (rpm)}\\ \text{Charge density (t/m}^{\text{3}}\text{)}\\ \text{No-load power (kw)}\\ \text{Gross power (grate) (kW)}\\ \text{Gross power (overflow) (kW)}\\ \text{R/D* factor (frac)}\\ Factor_D\text{ (frac)}\\ Factor_{LF}\text{ (frac)}\\ Factor_{CS}\text{ (frac)}\\ xm(small)\text{ (mm)}\\ xm(large)\text{ (mm)}\\ \end{bmatrix} & \begin{array}{ccc} \begin{bmatrix} d_1\text{ (mm)}\\ \vdots\\ d_n\text{ (mm)} \end{bmatrix} & \begin{bmatrix} (Q_m^P)_{11}\text{ (t/h)} & \dots & (Q_m^P)_{1m}\text{ (t/h)}\\ \vdots & \ddots & \vdots\\ (Q_m^P)_{n1}\text{ (t/h)} & \dots & (Q_m^P)_{nm}\text{ (t/h)}\\ \end{bmatrix} & \begin{bmatrix} \bar{d}_1\text{ (mm)}\\ \vdots\\ \bar{d}_{31}\text{ (mm)}\\ \end{bmatrix} & \begin{bmatrix} \frac{R_i}{D_i^*}_{11}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right) & \dots & \frac{R_i}{D_i^*}_{1m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right)\\ \vdots & \ddots & \vdots \\ \frac{R_i}{D_i^*}_{31,1}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right) & \dots & \frac{R_i}{D_i^*}_{31m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}/\text{h}\right)\\ \end{bmatrix} & \begin{bmatrix} \frac{R_i}{D_i}_{11}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right) & \dots & \frac{R_i}{D_i}_{1m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right)\\ \vdots & \ddots & \vdots \\ \frac{R_i}{D_i}_{31,1}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right) & \dots & \frac{R_i}{D_i}_{31m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right)\\ \end{bmatrix} & \begin{bmatrix} \ln \left( \frac{R_i}{D_i} \right)_{11} & \dots & \ln \left( \frac{R_i}{D_i} \right)_{1m}\\ \vdots & \ddots & \vdots \\ \ln \left( \frac{R_i}{D_i} \right)_{k1} & \dots & \ln \left( \frac{R_i}{D_i} \right)_{km}\\ \end{bmatrix}\\ \\ & & & & & \begin{bmatrix} \left( \frac{R_i}{D_i} \right)_{11}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right) & \dots & \left( \frac{R_i}{D_i} \right)_{1m}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right)\\ \vdots & \ddots & \vdots \\ \left( \frac{R_i}{D_i} \right)_{k1}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right) & \dots & \left( \frac{R_i}{D_i} \right)_{km}\left(\frac{\text{h}^\text{-1}}{\text{h}^\text{-1}}\right)\\ \end{bmatrix}\\ \\ & & & & & \begin{bmatrix} (Factor_{WI})_1 & \dots & (Factor_{WI})_m \end{bmatrix}\\ & & & & & &\\ & & & & & &\\ \end{array} \end{bmatrix} }[/math]
where:
- [math]\displaystyle{ \text{Mill volumetric feed rate} }[/math] is the flow rate of pulp into the mill (m3/h)
- [math]\displaystyle{ \text{Mill volume} }[/math] is the total volume inside the mill, calculated as the sum of a cylinder and two frustums (m3)
- [math]\displaystyle{ \text{Mill speed} }[/math] is the rotational rate of the mill (rpm)
- [math]\displaystyle{ \text{Charge density} }[/math] is the combined density of the charge, including grinding media, coarse ore, slurry and void space (t/m3)
- [math]\displaystyle{ \text{No-load power} }[/math] is the power input to the motor when the mill is rotating but empty (no balls, rocks or slurry) (kW)
- [math]\displaystyle{ \text{Gross power (grate)} }[/math] is the total power input to the motor if the mill is configured with a grate discharge (kW)
- [math]\displaystyle{ \text{Gross power (overflow)} }[/math] is the total power input to the motor if the mill is configured with an overflow discharge (kW)
- [math]\displaystyle{ \text{R/D* factor}=D_i^*/D_i }[/math] is the discharge rate scaling factor
- [math]\displaystyle{ Q_m^P }[/math] is the mass flow rate of particles in the mill product (t/h)
- [math]\displaystyle{ \bar{d}_i }[/math] is the geometric mean size of the internal mesh series interval that mass is retained on (mm)
Example
The images below show the selection of input arrays and output results in the Excel interface.
SysCAD
The SysCAD interface for steady-state (ProBal) mode is described below. For SysCAD Dynamic, see Ball Mill (Perfect Mixing, Dynamic).
ScdMD*BallMill page
The first tab page in the access window will have this name.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Tag | Display | This name tag may be modified with the change tag option. |
| Condition | Display | OK if no errors/warnings, otherwise lists errors/warnings. |
| ConditionCount | Display | The current number of errors/warnings. If condition is OK, returns 0. |
| GeneralDescription / GenDesc | Display | This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.
If this field is blank, then SysCAD will display the unit class ID. |
| Requirements | ||
| On | CheckBox | This enables the unit. If this box is not checked, then the material will pass straight through the mill with no change to the size distribution. |
| Method | Perfect Mixing | The Perfect Mixing model is used to determine the mill product size distribution. Different parameters can be used for different solids. |
| Herbst-Fuerstenau | The Herbst-Fuerstenau model is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Options | ||
| ShowQFeed | CheckBox | QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream. |
| ShowQProd | CheckBox | QProd and associated tab pages (eg Sp) will become visible, showing the properties of the products. |
| PowerModels | CheckBox | Show alternative tumbling mill power model calculations on the Power page. |
| MediaTrajectory | CheckBox | Show mill media rolling, sliding and free flight trajectory computations on the MediaTraj page. |
| OverfillingIndicator | CheckBox | Show overflow ball mill slurry volume, residence time, and overfilling evaluation on Overfilling page. |
| SizeForPassingFracCalc | Input (global) | Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section. |
| FracForPassingSizeCalc | Input (global) | Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section. |
| Stream Summary | ||
| MassFlow / Qm | Display | The total mass flow in each stream. |
| SolidMassFlow / SQm | Display | The Solids mass flow in each stream. |
| LiquidMassFlow / LQm | Display | The Liquid mass flow in each stream. |
| VolFlow / Qv | Display | The total Volume flow in each stream. |
| Temperature / T | Display | The Temperature of each stream. |
| Density / Rho | Display | The Density of each stream. |
| SolidFrac / Sf | Display | The Solid Fraction in each stream. |
| LiquidFrac / Lf | Display | The Liquid Fraction in each stream. |
| Passing | Display | The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream. |
| Passes | Display | The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction. |
Mill page
The Mill page is used to specify the input parameters for the mill model.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| PerfectMixing | ||
| HelpLink | Opens a link to this page using the system default web browser. Note: Internet access is required. | |
| Ball | ||
| MediaStringsP50 | CheckBox |
|
| Diameter | Input | The inside liner diameter of the original and simulated ball mills. |
| BellyLength | Input | The inside liner belly length of the simulated ball mill, excluding cones. |
| ConeAngle | Input | Angle of the feed and discharge end cones, measured as positive displacement from the vertical direction. |
| TrunnionDiameter | Input | The inside liner trunnion diameter of the simulated ball mill. |
| LoadFrac | Input | The volumetric load fraction of the original and simulated ball mills. |
| FracCS | Input | The fraction critical speed of the original and simulated ball mills. |
| WorkIndex | Input | Bond Ball Work Index of ore in the original mill. |
| BallSize | Input | Characteristic diameter of balls in original and simulated ball mills. |
| MaxBreakageRateFactor / K | Input | Parameter relating ball size and the size at which the breakage rate per discharge rate is maximum. |
| R/DFunction | ||
| NumSplineKnots | Input | Number of spline knots for the [math]\displaystyle{ R_i/D_i^* }[/math] function. |
| Size | Input | Spline knot size positions. |
| Ln(R/D*) | Input | Values of [math]\displaystyle{ \ln R/D^* }[/math] at each spline knot position. |
| Power | ||
| BallVolume | Input | Volumetric fraction of mill occupied by balls and voids. |
| VoidFillFraction | Input | Volumetric fraction of void space between balls occupied by slurry. |
| BallSG | Input | Specific Gravity or density of ball media. |
| Results | ||
| MillVolume | Display | Volume inside mill, including cones. |
| MillSpeed | Display | Rotational speed of simulated mill. |
| ChargeDensity | Display | Density of charge in simulated mill, including balls, solids and liquids. |
| NoLoadPower | Display | Power draw of empty mill (no balls, solids or liquids) |
| GrossPower.Grate | Display | Gross power draw of mill in grate configuration |
| GrossPower.Overflow | Display | Gross power draw of mill in overflow configuration |
Ore page
This page is used to define the comminution properties of SysCAD species with the size distribution quality in the project.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Appearance | ||
| DefaultAppearance | Sets all species to the default Broadbent-Callcott Appearance function. | |
| OreSpecific | CheckBox |
|
| Appearance | Input | User-specified Appearance function data for all species with size distribution property. |
| WorkIndex | ||
| WorkIndex.Sim | Input | Bond Ball Work Index data for all species with size distribution property. |
Ri/Di page
This page displays the scaling factors and breakage rate per discharge rate for each size interval computed by the Perfect Mixing model.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Scaling | ||
| RDStar/RD | Display | Value of the [math]\displaystyle{ \frac{R}{D^*} \bigg/ \frac{R}{D} }[/math] factor for discharge rate scaling. |
| Diameter | Display | Value of the mill diameter factor for rate scaling. |
| LoadFraction | Display | Value of the load fraction factor for rate scaling. |
| FracCS | Display | Value of the fraction critical speed factor for rate scaling. |
| WorkIndex | Display | Value of the Work Index factor of each ore species for rate scaling. |
| Ri/DiStar | ||
| Size | Display | Size of each interval in internal mesh series. |
| MeanSize | Display | Geometric mean size of each interval in internal mesh series. |
| Ri/DiStar | Display | Value of normalised [math]\displaystyle{ R_i/D_i^* }[/math] rate for each size interval, for each ore species. |
| Ri/Di | ||
| Size | Display | Size of each interval in internal mesh series. |
| MeanSize | Display | Geometric mean size of each interval in internal mesh series. |
| Ri/Di | Display | Value of [math]\displaystyle{ R_i/D_i }[/math] rate for each size interval, for each ore species. |
Power page
This optional page displays the inputs and results for alternative mill power models. The page is only visible if PowerModels is selected on the ScdMD*BallMill page.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Power | ||
MediaTraj page
This page displays the inputs and results for tumbling mill media trajectory calculations. The page is only visible if MediaTrajectory is selected on the ScdMD*BallMill page.
Overfilling page
This page displays the inputs and results for overflow discharge mill overfilling calculations. The page is only visible if Overfilling is selected on the ScdMD*BallMill page.
About page
This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| About | ||
| HelpLink | Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required. | |
| Information | Copies Product and License information to the Windows clipboard. | |
| Product | ||
| Name | Display | Met Dynamics software product name |
| Version | Display | Met Dynamics software product version number. |
| BuildDate | Display | Build date and time of the Met Dynamics Models SysCAD Add-On. |
| License | ||
| File | This is used to locate a Met Dynamics software license file. | |
| Location | Display | Type of Met Dynamics software license or file name and path of license file. |
| SiteCode | Display | Unique machine identifier for license authorisation. |
| ReqdAuth | Display | Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime. |
| Status | Display | License status, LICENSE_OK indicates a valid license, other messages report licensing errors. |
| IssuedTo | Display | Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to. |
| ExpiryDate | Display | Only visible if Met Dynamics license file is used. License expiry date. |
| DaysLeft | Display | Only visible if Met Dynamics license file is used. Days left before the license expires. |
See also
References
- ↑ 1.0 1.1 Napier-Munn, T.J., Morrell, S., Morrison, R.D. and Kojovic, T., 1996. Mineral comminution circuits: their operation and optimisation. Julius Kruttschnitt Mineral Research Centre, Indooroopilly, QLD.
- ↑ King, R.P., 2012. Modeling and Simulation of Mineral Processing Systems. Elsevier.
- ↑ Gupta, A. and Yan, D.S., 2016. Mineral processing design and operations: an introduction. Elsevier.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedNapier-Munn_et_al._(1996) - ↑ Morrell, S., 1996. Power draw of wet tumbling mills and its relationship to charge dynamics. Pt. 2: an empirical approach to modelling of mill power draw. Transactions of the Institution of Mining and Metallurgy. Section C. Mineral Processing and Extractive Metallurgy, 105.