AG/SAG Mill (Variable Rates): Difference between revisions
imported>Scott.Munro m (→Model theory) |
imported>Scott.Munro m (→Model theory) |
||
| Line 9: | Line 9: | ||
{{Under construction|section}} | {{Under construction|section}} | ||
<!-- | <!-- | ||
Introductory text here. | |||
Algorithm block diagram somewhere here. Calculation sequence. As implemented, especially ball-ore since combined ore SG can change during solve. | |||
=== Perfect mixing model === | === Perfect mixing model === | ||
Perfect | The Perfect Mixing model is based on a population balance of particles entering the mill, breaking into smaller sizes, and discharging as product. For a mill operating in steady-state, the diagram in Figure 1 below represents the balance for a given size fraction: | ||
::::{| | |||
| style="padding: 10px"|<gallery mode="nolines" widths=950px heights=36px> | |||
File:BallMillPerfectMixing1.png|Figure 1. Schematic diagram of the steady-state population balance adopted by the Perfect Mixing model. | |||
</gallery> | |||
|} | |||
The steady-state population balance is formulated mathematically as:{{Valery_and_Morrell_(1995)}} | |||
:<math>f_i + \sum_{j=1}^{i-1}A_{ij}R_js_j - (R_is_i-A_{ii}R_is_i) - p_i = 0</math> | |||
where: | |||
* <math>i</math> is the index of the size interval, <math>i = \{1,2,\dots,n\}</math>, <math>n</math> is the number of size intervals | |||
* <math>f_i</math> is the mass flow rate of solids of size interval <math>i</math> in the mill feed | |||
* <math>p_i</math> is the mass flow rate of solids of size interval <math>i</math> in the mill product | |||
* <math>s_i</math> is the mass of solids of size interval <math>i</math> in the mill load | |||
* <math>R_i</math> is the breakage rate of solids of size interval <math>i</math> in the mill load | |||
* <math>A_{ij}</math> is the appearance function, the distribution of particle mass arising from the breakage of a parent particle in size interval <math>j</math> into progeny of size interval <math>i</math> | |||
As the mill is perfectly mixed, the product is related to the mill contents and discharge rate as: | |||
:<math>p_i=D_is_i</math> | |||
where <math>D_i</math> is the rate of discharge of solids in size interval <math>i</math> from the mill. | |||
Therefore, the mill load at steady-state can be computed from: | |||
:<math>s_i= \dfrac{f_i + \sum\limits_{j=1}^{i-1}{A_{ij} R_j s_j}}{D_i + R_i - A_{ii} R_i}</math> | |||
and the product <math>p_i</math> subsequently determined. | |||
Liquids retained in the mill at steady-state are similarly determined from: | |||
:<math>f_{\rm w} - D_{\rm w} s_{\rm w} = 0</math> | |||
where: | |||
* <math>s_{\rm w}</math> is the load mass of water in the mill | |||
* <math>f_{\rm w}</math> is the mass feed rate of water into the mill | |||
* <math>D_{\rm w}</math> is the discharge rate of water from the mill, normally assumed to equal the value of <math>D_i</math> at the finest size interval. | |||
=== Slurry flow === | === Slurry flow === | ||
The volumetric flow rate of slurry discharged from a grated mill is a function of the slurry hold-up within the mill, in a manner analogous to flow from the bottom of a filled tank. | |||
In a steady-state model, the discharge flow rate is equal to the feed flow rate by definition. The following empirical relationship is used to estimate slurry hold-up in a grated mill for a given discharge flow rate:{{Napier-Munn et al. (1996)}} | |||
:<math>L_{\rm V} = m_1 \left ( \dfrac{F}{V} \right )^{m_2}</math> | |||
where: | |||
* <math>L_{\rm V}</math> is the fraction of mill volume occupied by below grate size solids and water (v/v) | |||
* <math>F</math> is the volumetric flow rate of slurry discharged from the mill (m<sup>3</sup>/min) | |||
* <math>m_1</math> is a constant related to grate design and mill speed | |||
* <math>m_2</math> is a constant assumed to take the value of 0.5.{{Kojovic et al. (2012)}} | |||
[[ | The volume of the mill, <math>V</math>, is calculated as the sum of a cylinder and two right circular frustums:{{Gupta and Yan (2016)}} | ||
:<math>V = \pi {R_{\rm m}}^2L + 2 \cdot \bigg[ \dfrac{\pi}{3} (R_{\rm m} - R_{\rm t}) \cdot \tan \alpha_{\rm c} \cdot \left ( {R_{\rm m}}^{2} + R_{\rm m} R_{\rm t} + {R_{\rm t}}^{2} \right) \bigg]</math> | |||
where: | |||
* <math>R_{\rm m}</math> is the radius of the mill inside the liners (m), equal to half of the diameter of the mill inside the liners, <math>D</math> (m) | |||
* <math>R_{\rm t}</math> is the radius of the discharge trunnion (m), equal to half of the diameter of the discharge trunnion, <math>D_{\rm t}</math> (m) | |||
* <math>L</math> is the length of the cylindrical (belly) section of the mill (m) | |||
* <math>\alpha_{\rm c}</math> is the cone angle, measured as the angular displacement of the cone surface from the vertical direction (rad) | |||
Morrell and Stephenson (1996) related discharge flow rate to slurry hold-up, grate design and mill speed with the following semi-empirical relation:{{Morrell and Stephenson (1996)}} | |||
:<math>Q_{\rm m} = k_{\rm m} {J_{\rm pm}}^2 \gamma^{2.5} A \phi^{-1.34} D^{0.5}</math> | |||
where | |||
* <math>Q_{\rm m}</math> is the volumetric discharge rate of slurry through the grinding media zone (m<sup>3</sup>/h) | |||
* <math>k_{\rm m}</math> is the slurry discharge coefficient for the grinding media zone | |||
* <math>J_{\rm pm}</math> is the net fractional slurry hold-up in the grinding media interstices (v/v) | |||
* <math>A</math> is the total open area of grate apertures (m<sup>2</sup>) | |||
* <math>\phi</math> is the fraction critical speed of the mill (frac) | |||
* <math>D</math> is the mill diameter (m) | |||
and the mean radial position of the grate apertures, <math>\gamma</math> (m/m), is defined as: | |||
:<math>\gamma = \frac{\sum{r_ia_i}}{r_{\rm m} \sum{a_i}}</math> | |||
where: | |||
* <math>a_i</math> is the open area of all holes (m<sup>2</sup>) at radial position <math>r_i</math> (m) | |||
* <math>r_{\rm m}</math> is the radius of the mill inside the liners (m) | |||
In addition, solids greater than diameter <math>x_{\rm m}</math> but less than the grate aperture size will also discharge from the mill. To estimate total discharge flow rate, <math>Q</math> (m<sup>3</sup>/h), Morrell and Stephenson (1996) suggest the following correction: | |||
:<math>Q = k_{\rm g} Q_{\rm m}</math> | |||
where <math>k_{\rm g}</math> is a factor to account for coarse material, and taking the values shown in Table 1. | |||
:{| class="wikitable" | |||
|+ Table 1. Applied values for <math>k_{\rm g}</math>. | |||
|- | |||
! Aperture !! <math>k_{\rm g}</math> | |||
|- | |||
| Grates only; <19mm || 1.07 | |||
|- | |||
| Grates only; 19mm - 28mm|| 1.125 | |||
|- | |||
| Grates >38mm or pebble ports || 1.2 | |||
|} | |||
The value of <math>m_1</math> for a given grate design and mill can be determined by observing that <math>L_{\rm V} = J_{\rm pm}</math> and <math>F = Q \big / 60</math> in the above equations.{{Kojovic et al. (2012)}} That is: | |||
:<math>m_1 \left ( \dfrac{Q}{60V} \right )^{0.5} = {k_{\rm g}}^{-0.5} {k_{\rm m}}^{-0.5} Q^{0.5} \gamma^{-1.25} A^{-0.5} \phi^{0.67} D^{-0.25}</math> | |||
The mill volume, <math>V</math>, can expressed as the product of the mill cross sectional area and an ''equivalent grinding length'', <math>L_{\rm eq}</math> (m), i.e.: | |||
:<math>V = \pi \left ( \dfrac{D}{2} \right )^2 L_{\rm eq} \implies L_{\rm eq} = \dfrac{V}{\pi \left ( \frac{D}{2} \right )^2}</math> | |||
Furthermore, the total open area of the grates, <math>A</math> (m<sup>2</sup>), can be replaced with an expression combining the grate ''open area fraction'', <math>A_{\rm OF}</math> (m<sup>2</sup>/m<sup>2</sup>), and mill cross-sectional area: | |||
:<math>A = \pi \left ( \dfrac{D}{2} \right )^2 A_{\rm OF}</math> | |||
Replacing the <math>V</math> and <math>A</math> terms in the <math>m_1</math> equation above yields: | |||
:<math>m_1 = \sqrt{60} \cdot ({k_{\rm g}} {k_{\rm m}})^{-0.5} \gamma^{-1.25} {A_{\rm OF}}^{-0.5} \phi^{0.67} D^{-0.25} {L_{\rm eq}}^{0.5}</math> | |||
Thus, slurry hold-up can be computed for a given feed/discharge flow rate, grate design and mill. | |||
=== Discharge rates === | |||
[[File:AGSAGVariableRates7.png|thumb|425px|Figure X. Classification function, <math>C_i</math>, with pebble port open are fraction, <math>f_p</math>, specified.]] | |||
[[File:AGSAGVariableRates7.png|thumb|425px|Figure X. Classification function, <math>C_i</math>, where pebble port open are fraction, <math>f_p</math>, is zero, i.e grates only.]] | |||
The discharge rate of solids from the grate of a perfectly mixed mill is:{{Kojovic et al. (2012)}} | |||
:<math>p_i = D_i.s_i</math> | |||
where: | |||
:<math>D_i = d_{\rm max}.C_i</math> | |||
:<math> C_i = | |||
\begin{cases} | |||
1 & \bar d_i \leq x_{\rm m}\\ | |||
\left ( 1 - \dfrac{\ln \bar d_i -\ln x_{\rm m}}{\ln x_{\rm g} - \ln x_{\rm m} } \right )(1 - f_{\rm p}) + f_{\rm p} & x_{\rm m}<\bar d_i\leq x_{\rm g}\\ | |||
\left ( 1 - \dfrac{\ln \bar d_i -\ln x_{\rm g}}{\ln x_{\rm p} - \ln x_{\rm g} } \right ) .f_{\rm p} & x_{\rm g}<\bar d_i\leq x_{\rm p}\\ | |||
0 & \bar d_i>x_{\rm p}\\ | |||
\end{cases} | |||
</math> | |||
and: | |||
* <math>d_{\rm max}</math> is the fraction of load presented to the mill discharge per unit of time (h<sup>-1</sup>) | |||
* <math>C_{i}</math> is the classification function, the fraction of particles of size <math>i</math> reporting to the mill product (frac) | |||
* <math>\bar d_i</math> is the [[Conversions|geometric mean size]] of particles in size interval <math>i</math> (mm) | |||
* <math>x_{\rm m}</math> is the particle size below which all mass in the size interval reports to mill product (mm), i.e. like water | |||
* <math>x_{\rm g}</math> is the grate aperture size (mm) | |||
* <math>x_{\rm p}</math> is the pebble port size (mm) | |||
* <math>f_{\rm p}</math> is the fraction of open area occupied by pebble ports (m<sup>2</sup>/m<sup>2</sup>) | |||
Figure X shows an example classification function with pebble ports included, whilst Figure x shows the same function with a grate-only mill. | |||
The value of <math>d_{\rm max}</math> is adjusted during the calculation sequence to ensure the fraction of solids less than <math>x_{\rm m}</math> plus water retained in the mill load computed by the [[AG/SAG Mill (Variable Rates)#Perfect_mixing_model|Perfect Mixing population balance]] matches the slurry hold-up determined by the [[AG/SAG Mill (Variable Rates)#Slurry_flow|slurry flow]] calculations. | |||
=== Breakage rates === | === Breakage rates === | ||
[[File:AGSAGVariableRates7.png|thumb|425px|Figure X. Breakage rate distribution characterised by cubic spline interpolation.]] | |||
The breakage rate at each size interval, <math>R_i</math> (h<sup>-1</sup>), is generated by [[Interpolation|cubic spline interpolation]] between five breakage rate knots (<math>R1 - R5</math>) at the 0.25, 4, 16, 44 and 128mm particle size positions.{{Leung et al. (1987)}} | |||
Morrell and Morrison (1996) described the following set of empirical equations which relate the breakage rate knots <math>R1 - R5</math> to mill operating conditions:{{Morrell and Morrison (1996)}} | |||
:<math> | |||
\begin{array}{l} | |||
\ln(R1) = \mathit{RConst}_1 + \dfrac{k_{11} + k_{12} \ln (R2) - k_{13} \ln (R3) + J_{\rm B} (k_{14} - k_{15} F_{80}) - D_{\rm B}}{S_{\rm b}}\\ | |||
\ln(R2) = \mathit{RConst}_2 + k_{21}+ k_{22}\ln(R3) - k_{23} \ln(R4) - k_{24} F_{80}\\ | |||
\ln(R3) = \mathit{RConst}_3 + S_{\rm a} + \dfrac{k_{31} + k_{32} \ln(R4) - k_{33} R_{\rm r}}{S_{\rm b}}\\ | |||
\ln(R4) = \mathit{RConst}_4 + S_{\rm b} (k_{41} + k_{42} \ln(R5) + J_{\rm B} (k_{43} - k_{44} F_{80}))\\ | |||
\ln(R5) = \mathit{RConst}_5 + S_{\rm a} + S_{\rm b} \left (k_{51} + k_{52} F_{80} + J_{\rm B} (k_{53} - k_{54} F_{80}) - 3.0 D_{\rm B} \right )\\ | |||
\end{array} | |||
</math> | |||
where: | |||
* <math>\mathit{RConst}_1 - \mathit{RConst}_5</math> are user-defined constants which can be used to adjust modelled breakage rates to observed values | |||
* <math>J_{\rm B}</math> is the fraction of total mill volume occupied by balls and associated voids (% v/v) | |||
* <math>F_{80}</math> is the 80% passing size of new feed (mm) | |||
* <math>k_{ij}</math> are the regression coefficients specified in Table 1 | |||
=== | :{| class="wikitable" | ||
|+ Table 1. Breakage rate regression coefficients. | |||
|- | |||
! <math>j</math> !! <math>k_{1j}</math> !! <math>k_{2j}</math> !! <math>k_{3j}</math> !! <math>k_{4j}</math> !! <math>k_{5j}</math> | |||
|- | |||
| 1 || 2.504|| 4.682|| 3.141|| 1.057|| 1.894 | |||
|- | |||
| 2 || 0.397|| 0.468|| 0.402|| 0.333|| 0.014 | |||
|- | |||
| 3 || 0.597|| 0.327|| 4.632 || 0.171|| 0.473 | |||
|- | |||
| 4 || 0.192|| 0.0085|| -|| 0.0014|| 0.002 | |||
|- | |||
| 5 || 0.002 || - || -|| -|| - | |||
|} | |||
The mill rotational speed scaling factor, <math>S_{\rm a}</math>, is computed from the mill rotational speed (rpm) as: | |||
:<math>S_{\rm a} = \ln \left ( \dfrac{\text{Mill speed (rpm)}}{23.6} \right )</math> | |||
Similarly, the mill fraction critical speed scaling factor, <math>S_{\rm b}</math>, is computed from the [[Tumbling Mill (Speed)|mill fraction critical speed]], <math>\phi</math> (frac), as: | |||
:<math>S_{\rm b} = \dfrac{\phi}{0.75}</math> | |||
The ball diameter scaling factor, <math>D_{\rm B}</math>, is computed from the ball top size, <math>d_{\rm B}</math> (mm), as: | |||
:<math>D_{\rm B} = \ln \left ( \dfrac{d_{\rm B}}{90} \right )</math> | |||
The recycle ratio, <math>R_{\rm r}</math>, is the ratio of the mass flowrate of recycled -20+4mm material to the total mass flowrate of all new feed plus recycled -20+4mm material, i.e. | |||
:<math>R_{\rm r} = \dfrac{Q_{\rm M,R} (P_{20\text{mm,R}} - P_{4\text{mm,R}})}{Q_{\rm M,F} + Q_{\rm M,R}(P_{20\text{mm,R}} - P_{4\text{mm,R}})}</math> | |||
where: | |||
* <math>Q_{\rm M,F}</math> is new feed mass flow rate (t/h) | |||
* <math>Q_{\rm M,R}</math> is recycle feed mass flow rate (t/h) | |||
* <math>P_{20\text{mm,R}}</math> and <math>P_{4\text{mm,R}}</math> are the fraction of recycle feed passing 20mm and 4mm size, respectively (frac) | |||
The recycle ratio, <math>R_{\rm r}</math>, is only applicable when the coarse recycled feed component consists of mill pebbles (scats) which have not undergone an intervening breakage step such as pebble crushing. | |||
=== Specific comminution energy === | === Specific comminution energy === | ||
S20 units in mm.{{Leung et al. (1987)}} | |||
:<math>S_{20} = \left (P_{100} \cdot P_{98} \cdot P_{96} \dots P_{80} \right )^{\frac{1}{11}} </math> | |||
Need to show selection of top size mesh for P100 versus other Ps. | |||
Energy level is potential energy of particle at S20 characteristic size and density falling through a the full height of the mill.{{{Leung et al. (1987)}} Energy level corrected from Leung for S20 radius in volume calc and units to kWh: | |||
:<math>\mathit{EL} = \dfrac{\frac{4}{3} \pi \left ( \frac{S_{20}}{2000} \right )^3 \rho g D}{3600}</math> | |||
Ecs.{{Bueno et al. (2013)}} | |||
:<math> | |||
(E_{\rm cs})_i = | |||
\begin{cases} | |||
\dfrac{\mathit{EL}}{\frac{4}{3} \pi \left ( \frac{\bar d_i}{2000} \right )^3 \rho} & i = 1\\ | |||
\dfrac{(E_{\rm cs})_1}{ \left ( \frac{\bar d_i}{\bar d_1} \right )^{1.5} } & 1 < i \leq n | |||
\end{cases} | |||
</math> | |||
1987, Leung, An energy based ore specific model for autogenous and semi-autogenous grinding, Copper '87.{{Leung et al. (1987)}} | 1987, Leung, An energy based ore specific model for autogenous and semi-autogenous grinding, Copper '87.{{Leung et al. (1987)}} | ||
=== | S20 calc here. | ||
Then E1 (or EL?) to Ecs per size. | |||
=== Appearance function === | |||
==== High energy ==== | |||
Also reference crusher model tn splines etc. But always fixed spline for this model. | |||
==== Low energy ==== | |||
==== Combined energy ==== | |||
=== Ball load === | === Ball load === | ||
Ball sizing root 2 convereted to full size, interpolation etc. | |||
Equivalent ball size | |||
Converts ball load to equivalent ore for S20 calc. | |||
If no ball load, autogenous milling. | |||
=== Internal mesh series === | |||
=== Multicomponent modelling === | |||
=== Mill power === | |||
Show equations for Jt etc to get inputs for Morrell power model. | |||
Default uses Morrell 1992, for info only. Other models can be applied, not directly used in calculations. | |||
=== Additional notes === | |||
An important, and potentially overlooked, limitation of the Variable Rates model is the insensitivity of the breakage rate relationships to mill load. Only valid at constant load, note about this. | |||
As-published model does not include slurry pool. Model excludes slurry pool in slurry flow and power model. | |||
--> | --> | ||
| Line 60: | Line 311: | ||
{{Excel (Text, Inputs)}} | {{Excel (Text, Inputs)}} | ||
:<math>Parameters= | :<math>\mathit{Parameters} = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
D\text{ (m)}\\ | D\text{ (m)}\\ | ||
| Line 67: | Line 318: | ||
\alpha_{c}\text{ (deg.)}\\ | \alpha_{c}\text{ (deg.)}\\ | ||
\phi\text{ (frac)}\\ | \phi\text{ (frac)}\\ | ||
A_{\rm OF}\text{ (m}^{\text{2}}\text{)}\\ | |||
f_{\rm p}\text{ (m}^2\text{/m}^2\text{)}\\ | f_{\rm p}\text{ (m}^2\text{/m}^2\text{)}\\ | ||
x_{\rm p}\text{ (mm)}\\ | x_{\rm p}\text{ (mm)}\\ | ||
| Line 86: | Line 337: | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
Size = \begin{bmatrix} | \mathit{Size} = \begin{bmatrix} | ||
d_{1}\text{ (mm)}\\ | d_{1}\text{ (mm)}\\ | ||
\vdots\\ | \vdots\\ | ||
| Line 92: | Line 343: | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
MillNewFeed= \begin{bmatrix} | \mathit{MillNewFeed} = \begin{bmatrix} | ||
(Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\ | (Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\ | ||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
| Line 98: | Line 349: | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
\mathit{OreSG} = \begin{bmatrix} | |||
( | (\rho_{\rm S})_{1}\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_{\rm S})_m\text{ (t/m}^\text{3}\text{)}\\ | ||
\end{bmatrix},\;\;\;\;\;\; | |||
</math> | |||
\end{bmatrix} | |||
:<math> | :<math> | ||
\mathit{BallSizing} = \begin{bmatrix} | |||
(\mathit{MF}_{\rm B})_{d_{\rm B}/\sqrt{2}}\text{ (}%\text{ w/w)}\\ | |||
(\mathit{MF}_{\rm B})_{d_{\rm B}/(2\sqrt{2}})\text{ (}%\text{ w/w)}\\ | |||
(\mathit{MF}_{\rm B})_{d_{\rm B}/(3\sqrt{2}})\text{ (}%\text{ w/w)}\\ | |||
(\mathit{MF}_{\rm B})_{d_{\rm B}/(4\sqrt{2}})\text{ (}%\text{ w/w)}\\ | |||
({ | |||
({ | |||
({ | |||
({ | |||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
RConst= \begin{bmatrix} | \mathit{RConst} = \begin{bmatrix} | ||
{ | \mathit{RConst}_1\\ | ||
\vdots\\ | \vdots\\ | ||
{ | \mathit{RConst}_5\\ | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
OreBreakageParams= | \mathit{OreBreakageParams} = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
A_1 & \dots & | A_1 & \dots & A_m\\ | ||
b_1 & \dots & | b_1 & \dots & b_m\\ | ||
(t_{\rm a})_1 & \dots & (t_{\rm a}) | (t_{\rm a})_1 & \dots & (t_{\rm a})_m\\ | ||
\end{bmatrix} | \end{bmatrix},\quad | ||
\mathit{MillRecycleFeed} = \begin{bmatrix} | |||
(Q_{\rm M,R})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,R})_{1m}\text{ (t/h)}\\ | |||
\vdots & \ddots & \vdots\\ | |||
(Q_{\rm M,R})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,R})_{nm}\text{ (t/h)}\\ | |||
\end{bmatrix}^* | |||
</math> | </math> | ||
where: | where: | ||
* <math>f_{\rm p}</math> is the pebble port area fraction (frac) | * <math>f_{\rm p}</math> is the pebble port area fraction (frac) | ||
* <math>x_{\rm p}</math> is the size of the pebble port aperture (mm) | * <math>x_{\rm p}</math> is the size of the pebble port aperture (mm) | ||
* <math>x_{\rm g}</math> is the size of the grate aperture (mm) | * <math>x_{\rm g}</math> is the size of the grate aperture (mm) | ||
* <math>x_{\rm m}</math> is the fine size (mm) | * <math>x_{\rm m}</math> is the fine size (mm) | ||
* <math>J_{\rm B}</math> is the ball load volume fraction (v/v) | * <math>J_{\rm B}</math> is the ball load volume fraction (v/v) | ||
* <math>\rho_{\rm B}</math> is the density or specific gravity of the ball media (t/m<sup>3</sup> or -) | * <math>\rho_{\rm B}</math> is the density or specific gravity of the ball media (t/m<sup>3</sup> or -) | ||
* <math>(F_{80})_{\rm Ref}</math> is the reference ''F<sub>80</sub>'' size (mm) | * <math>(F_{80})_{\rm Ref}</math> is the reference ''F<sub>80</sub>'' size (mm) | ||
* <math>(d_1)_{\rm Int}</math> is the internal mesh top size (mm) | * <math>(d_1)_{\rm Int}</math> is the internal mesh top size (mm) | ||
| Line 159: | Line 401: | ||
* <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm) | * <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm) | ||
* <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm) | * <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm) | ||
* <math>\rho_{\rm S}</math> is the density or specific gravity of solids (t/m<sup>3</sup> or -) | * <math>\rho_{\rm S}</math> is the density or specific gravity of solids (t/m<sup>3</sup> or -) | ||
* <math>{ | * <math>\mathit{MF}_{\rm B}</math> is the mass fraction retained of balls (% w/w) | ||
* <math>A</math> (%), <math>b</math>, and <math>t_{\rm a}</math> are ore breakage parameters | * <math>A</math> (%), <math>b</math>, and <math>t_{\rm a}</math> are ore breakage parameters | ||
* <math>^*</math> indicates the <math>\mathit{MillRecycleFeed}</math> array is an optional input parameter, and is set to null if omitted | * <math>^*</math> indicates the <math>\mathit{MillRecycleFeed}</math> array is an optional input parameter, and is set to null if omitted | ||
| Line 193: | Line 431: | ||
d_{\rm Max}\text{ (h}^{-1}\text{)}\\ | d_{\rm Max}\text{ (h}^{-1}\text{)}\\ | ||
S_{20}\text{ (mm)}\\ | S_{20}\text{ (mm)}\\ | ||
{ | \mathit{EL}\text{ (kWh)}\\ | ||
\rho_{\rm c}\text{ (t/m}^3\text{)}\\ | \rho_{\rm c}\text{ (t/m}^3\text{)}\\ | ||
\theta_{\rm S}\text{ (rad)}\\ | \theta_{\rm S}\text{ (rad)}\\ | ||
| Line 697: | Line 935: | ||
{{SysCAD (Page, About)}} | {{SysCAD (Page, About)}} | ||
== See also == | |||
* [[Tumbling Mill (Slurry Flow)]] | |||
== References == | == References == | ||
Revision as of 03:20, 20 August 2024
Description
This article describes an implementation of the Autogenous (AG) and Semi-Autogenous (SAG) mill model originated by Leung (1987) and extended with variable breakage rates by Morrell and Morrison (1996).[1][2][3]
The formulation is referred to in the associated literature as the "Variable Rates" model (Morrell et al., 2001).[4]
Model theory
Excel
The Variable Rates AG/SAG mill model may be invoked from the Excel formula bar with the following function call:
=mdUnit_AGSAG_VariableRates(Parameters as Range, Size as Range, MillNewFeed as Range, OreSG as Range, BallSizing as Range, RConst as Range, OreBreakageParams as Range, Optional MillRecycleFeed as Range = Nothing)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:
where:
- is the pebble port area fraction (frac)
- is the size of the pebble port aperture (mm)
- is the size of the grate aperture (mm)
- is the fine size (mm)
- is the ball load volume fraction (v/v)
- is the density or specific gravity of the ball media (t/m3 or -)
- is the reference F80 size (mm)
- is the internal mesh top size (mm)
- is the charge void fraction (v/v)
- is the mass flow feed rate of liquids into the mill (t/h)
- is the Specific Gravity or density of liquids in the feed (- or t/m3)
- is an index of the Appearance function to view in the results
- is an index of the Appearance function to view in the results
- is the number of intervals
- is the number of ore types
- is the size of the square mesh interval that feed mass is retained on (mm)
- , i.e. descending size order from top size () to sub mesh ( mm)
- is the density or specific gravity of solids (t/m3 or -)
- is the mass fraction retained of balls (% w/w)
- (%), , and are ore breakage parameters
- indicates the array is an optional input parameter, and is set to null if omitted
Results
The results are displayed in Excel as an array corresponding to the matrix notation below:
where:
- is the number of internal computation steps required to converge the load
- is the numerical error of the converged load approximation
- is the flow rate of pulp into the mill (m3/h)
- is the total volume inside the mill, calculated as the sum of a cylinder and two frustums (m3)
- is the rotational rate of the mill (rpm)
- is the mass of ore solids in the mill (t)
- is the mass of liquids in the mill (t)
- is the mass of balls in the mill (t)
- is the total mass of ore, liquids and balls in the mill (t)
- is the charge volume fraction (v/v)
- is the void fill fraction (v/v)
- is the coarse factor (-)
- is a parameter of the Austin mill holdup equation
- is a parameter of the Austin mill holdup equation
- is maximum discharge rate from the mill (h-1)
- is the geometric mean size of the top 20% of the load (mm)
- is the energy level in the mill (kWh)
- is the charge density (t/m3)
- is angular position of the charge shoulder (rad)
- is angular position of the charge toe (rad)
- is the charge surface radius (m)
- is the no-load power of the mill (kW)
- is the net power of the mill (kW)
- is the gross power of the mill (kW)
- is product mass flow rate (t/h)
- is the geometric mean size of the internal mesh series interval that mass is retained on (mm)
- is the discharge rate (h-1)
- is the breakage rate (h-1)
- is specific comminution energy (kWh/t)
- is the Appearance function (frac)
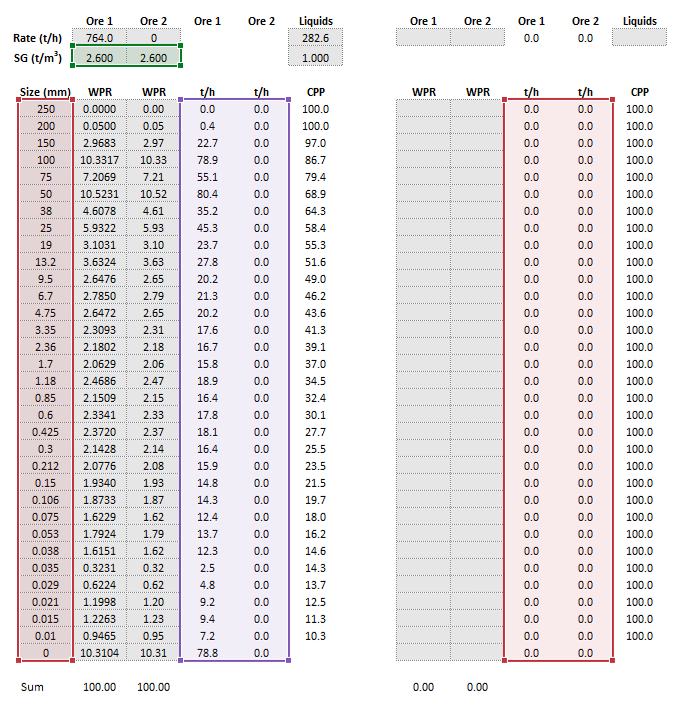
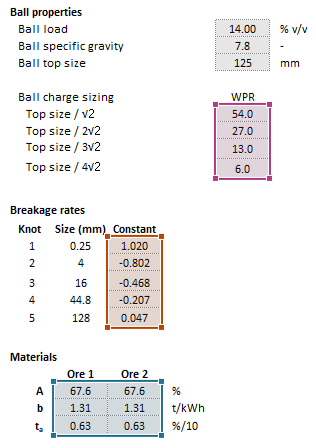
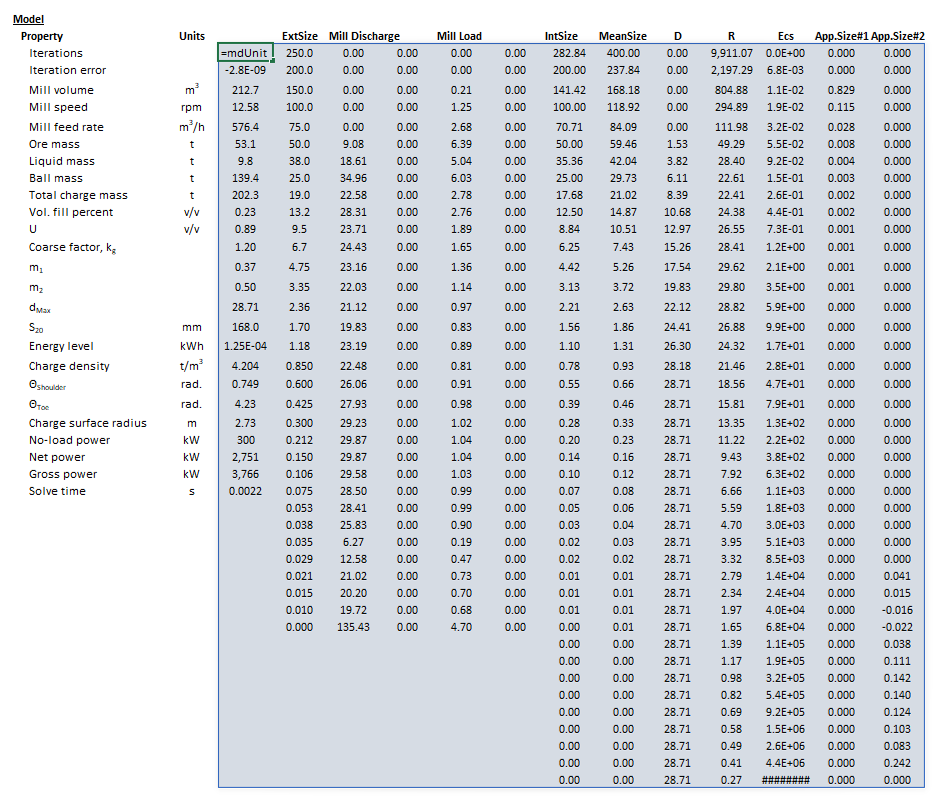
Example
The images below show the selection of input arrays and output results in the Excel interface.
SysCAD
The sections and variable names used in the SysCAD interface are described in detail in the following tables.
MD_Mill page
The first tab page in the access window will have this name.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Tag | Display | This name tag may be modified with the change tag option. |
| Condition | Display | OK if no errors/warnings, otherwise lists errors/warnings. |
| ConditionCount | Display | The current number of errors/warnings. If condition is OK, returns 0. |
| GeneralDescription / GenDesc | Display | This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.
If this field is blank, then SysCAD will display the unit class ID. |
| Requirements | ||
| On | CheckBox | This enables the unit. If this box is not checked, then the material will pass straight through the mill with no change to the size distribution. |
| NumParallelUnits | Input | The number of parallel, identical units to simulate:
|
| Method | Fixed Discharge | The discharge particle size distribution is user defined. Different distributions can be used for different solids. |
| AG/SAG (Variable Rates) | The Variable Rates AG/SAG mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Rod Mill (Lynch) | The Lynch rod mill model is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Ball (Perfect Mixing) | The Perfect Mixing ball mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Stirred (Perfect Mixing) | The Perfect Mixing stirred mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| Mill (Herbst-Fuerstenau) | The Herbst-Fuerstenau model is used to determine the mill product size distribution. Different parameters can be used for different solids. | |
| PowerModels | CheckBox | Show alternative mill power model calculations on the Power page. |
| MediaTrajectory | CheckBox | Show mill media rolling, sliding and free flight trajectory computations on the MediaTraj page. |
| MediaStrings | CheckBox | Show media size distributions at recharge equilibrium on the MediaStrings page. |
| Options | ||
| ShowQFeed | CheckBox | QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream. |
| ShowQProd | CheckBox | QProd and associated tab pages (eg Sp) will become visible, showing the properties of the products. |
| SizeForPassingFracCalc | Input | Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section. |
| FracForPassingSizeCalc | Input | Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section. |
| Stream Summary | ||
| MassFlow / Qm | Display | The total mass flow in each stream. |
| SolidMassFlow / SQm | Display | The Solids mass flow in each stream. |
| LiquidMassFlow / LQm | Display | The Liquid mass flow in each stream. |
| VolFlow / Qv | Display | The total Volume flow in each stream. |
| Temperature / T | Display | The Temperature of each stream. |
| Density / Rho | Display | The Density of each stream. |
| SolidFrac / Sf | Display | The Solid Fraction in each stream. |
| LiquidFrac / Lf | Display | The Liquid Fraction in each stream. |
| Passing | Display | The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream. |
| Passes | Display | The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction. |
Mill page
The Mill page is used to specify the input parameters for the mill model.
Ore page
This page is used to define the comminution properties of SysCAD species with the size distribution quality in the project.
Results page
This page is used to display the model results.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Results | ||
| Solver | ||
| Iterations | Display | Number of iterations to converge internal load solver. |
| IterationError | Display | Numerical approximation error of internal load solver. |
| Mill Properties | ||
| MillVolume | Display | Internal volume of the mill. |
| MillSpeed | Display | Rotational speed of the mill. |
| MillFeedRate / Feed.SLQv | Display | Volumetric feed rate of pulp into the mill. |
| Mill Contents | ||
| OreMass | Display | Mass of ore (solids with PSD) in the mill. |
| LiquidMass | Display | Mass of liquids in the mill. |
| BallMass | Display | Mass of ball media in the mill. |
| TotalChargeMass | Display | Total mass of ore, liquids and balls in the mill. |
| VolTotalLoad | Display | Volumetric fraction of mill volume of total charge (ore, liquids, balls and void space). |
| Mill Discharge | ||
| m1 | Display | Parameter of the Austin mill holdup relationship. |
| m2 | Display | Parameter of the Austin mill holdup relationship. |
| dMax | Display | Maximum discharge rate of load volume through the grate. |
| Charge Properties | ||
| S20 | Display | Size of the top (largest) 20% of the load. |
| ChargeDensity | Display | Density of the charge. |
| U | Display | Fraction of charge void space filled with slurry. |
| ThetaShoulder | Display | Angular position of the charge shoulder. |
| ThetaTue | Display | Angular position of the charge toe. |
| ChargeSurfaceRadius | Display | Radius of the inner charge surface. |
| Power | ||
| NoLoadPower | Display | No-load power draw of the mill. |
| NetPower | Display | Net power draw of the mill. |
| GrossPower | Display | Gross power draw of the mill. |
RiDi page
This page displays the breakage and discharge rates for each size interval computed by the model.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Rates | ||
| Size | Display | Size of each interval in internal mesh series. |
| MeanSize | Display | Geometric mean size of each interval in internal mesh series. |
| R | Display | Value of breakage rate, , for each size interval, for each ore species. |
| D | Display | Value of discharge rate, , for each size interval. |
| Ecs | Display | Value of the specific comminution energy for each size interval. |
Load page
This page displays information about the balls, solids and liquids that currently comprise the mill load.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Distribution | ||
| Name | Display | Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream. |
| IntervalCount | Display | Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream. |
| SpWithPSDCount | Display | Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality. |
| Load | ||
| SolidMass / SMt | Display | The mass of solids with the SysCAD size distribution property currently in the mill. |
| LiquidMass / LMt | Display | The mass of liquids plus solids without the SysCAD size distribution property currently in the mill. |
| BallMass / BMt | Display | The mass of ball media in the mill. |
| Size | Display | Size of each interval in the external mesh series. |
| MeanSize | Display | Geometric mean size of each interval in the external mesh series. |
| Load | Display | The mass of solids with the SysCAD size distribution property currently in the mill, by size and species. |
Power page
This optional page displays the inputs and results for alternative mill power models. The page is only visible if PowerModels is selected on the MD_Mill page.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Power | ||
| HoggFuerstenau | CheckBox | Shows inputs and results for tumbling mill power calculations using the Hogg and Fuerstenau method. |
| MorrellC | CheckBox | Shows inputs and results for tumbling mill power calculations using the Morrell Continuum method. |
| MorrellE | CheckBox | Shows inputs and results for tumbling mill power calculations using the Morrell Empirical method. |
| MorrellD | CheckBox | Shows inputs and results for tumbling mill power calculations using the Morrell Discrete Shell method. |
| HildenPowell | CheckBox | Shows inputs and results for tumbling mill power calculations using the Hilden and Powell method. |
MediaStrings page
This page displays the inputs and results for grinding mill media string calculations. The page is only visible if MediaStrings is selected on the MD_Mill page.
MediaTraj page
This page displays the inputs and results for tumbling mill media trajectory calculations. The page is only visible if MediaTrajectory is selected on the MD_Mill page.
About page
This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| About | ||
| HelpLink | Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required. | |
| Information | Copies Product and License information to the Windows clipboard. | |
| Product | ||
| Name | Display | Met Dynamics software product name |
| Version | Display | Met Dynamics software product version number. |
| BuildDate | Display | Build date and time of the Met Dynamics Models SysCAD Add-On. |
| License | ||
| File | This is used to locate a Met Dynamics software license file. | |
| Location | Display | Type of Met Dynamics software license or file name and path of license file. |
| SiteCode | Display | Unique machine identifier for license authorisation. |
| ReqdAuth | Display | Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime. |
| Status | Display | License status, LICENSE_OK indicates a valid license, other messages report licensing errors. |
| IssuedTo | Display | Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to. |
| ExpiryDate | Display | Only visible if Met Dynamics license file is used. License expiry date. |
| DaysLeft | Display | Only visible if Met Dynamics license file is used. Days left before the license expires. |
See also
References
- ↑ Napier-Munn, T.J., Morrell, S., Morrison, R.D. and Kojovic, T., 1996. Mineral comminution circuits: their operation and optimisation. Julius Kruttschnitt Mineral Research Centre, Indooroopilly, QLD.
- ↑ Leung, K., Morrison, R.D. and Whiten, W.J., 1987. An Energy Based Ore Specific Model for Autogenous and Semi-autogenous Grinding, Copper 87, Vina del Mar, Vol. 2, pp 71 - 86
- ↑ Morrell, S. and Morrison, R.D., 1996. AG and SAG mill circuit selection and design by simulation. In International Conference on Autogenous and Semiautogenous Grinding Technology (Vol. 2, pp. 769-790).
- ↑ Morrell, S., Valery, W., Banini, G. and Latchireddi, S., 2001. Developments in AG/SAG mill modelling. Proceedings of Autogenous and Semiautogenous Grinding Technology, Vancouver, pp.71-84.