AG/SAG Mill (Variable Rates): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
m (1 revision imported)
imported>Scott.Munro
 
(11 intermediate revisions by the same user not shown)
Line 6: Line 6:


== Model theory ==
== Model theory ==
{{Restricted content}}


{{Under construction|section}}
<hide>
[[File:AGSAGVariableRates7.png|thumb|450px|Figure 1. Schematic diagram of internal AG/SAG mill processes (after Napier-Munn et al., 1996).{{Napier-Munn et al. (1996)}}]]
 
[[File:AGSAGVariableRates8.png|thumb|450px|Figure 3. Variable Rates AG/SAG mill model iterative calculation sequence (after Napier-Munn et al., 1996).{{Napier-Munn et al. (1996)}}]]
 
The schematic diagram in Figure 1 illustrates the primary processes of ''feed'', ''breakage'', ''classification'' and ''discharge'' occurring within AG/SAG mills.
 
The Variable Rates AG/SAG model ties these processes together through the ''perfect mixing model'', which is based on a population balance of particles entering the mill, breaking into smaller sizes, and discharging as product. For a mill operating in steady-state, the diagram in Figure 2 below represents the balance for a given size fraction:
 
::::{|
| style="padding: 10px"|<gallery mode="nolines" widths=950px heights=36px>
File:BallMillPerfectMixing1.png|Figure 2. Schematic diagram of the steady-state population balance adopted by the Variable Rates AG/SAG model.
</gallery>
|}
 
The steady-state population balance is formulated mathematically as:{{Valery_and_Morrell_(1995)}}
 
:<math>f_i + \sum_{j=1}^{i-1}A_{ij}R_js_j - (R_is_i-A_{ii}R_is_i) - p_i = 0</math>
 
where:
* <math>i</math> is the index of the size interval, <math>i = \{1,2,\dots,n\}</math>, <math>n</math> is the number of size intervals
* <math>f_i</math> is the volumetric flow rate of solids of size interval <math>i</math> in the mill feed (m<sup>3</sup>/h)
* <math>p_i</math> is the volumetric flow rate of solids of size interval <math>i</math> in the mill product (m<sup>3</sup>/h)
* <math>s_i</math> is the volume of solids of size interval <math>i</math> in the mill load (m<sup>3</sup>)
* <math>R_i</math> is the breakage rate of solids of size interval <math>i</math> in the mill load  (h<sup>-1</sup>)
* <math>A_{ij}</math> is the appearance function, the distribution of particle volume arising from the breakage of a parent particle in size interval <math>j</math> into progeny of size interval <math>i</math> (frac)
 
As the mill is perfectly mixed, the product is related to the mill contents and discharge rate as:
 
:<math>p_i=D_is_i</math>
 
where <math>D_i</math> is the rate of discharge of solids in size interval <math>i</math> from the mill (h<sup>-1</sup>).
 
Therefore, the mill load at steady-state can be computed from:
 
:<math>s_i= \dfrac{f_i + \sum\limits_{j=1}^{i-1}{A_{ij} R_j s_j}}{D_i + R_i - A_{ii} R_i}</math>
 
and the product <math>p_i</math> subsequently determined.
 
Liquids retained in the mill at steady-state are similarly determined from:
 
:<math>f_{\rm L} - D_{\rm L} s_{\rm L} = 0</math>
 
where:
* <math>s_{\rm L}</math> is the load volume of liquids in the mill (m<sup>3</sup>)
* <math>f_{\rm L}</math> is the volumetric feed rate of liquids into the mill (m<sup>3</sup>/h)
* <math>D_{\rm L}</math> is the discharge rate of liquids from the mill, normally assumed to equal <math>D_n</math> (h<sup>-1</sup>).
 
</hide><div class="user-show">
=== Calculation sequence ===
</div><hide>
 
The Variable Rates AG/SAG model uses a range of sub-models to quantify the breakage rate (<math>R</math>), appearance function (<math>A</math>), and discharge function (<math>D</math>) terms of the perfect mixing model, and hence compute the mill load (<math>s</math>) and product (<math>p</math>) at steady-state.
 
These sub-models are strongly interactive, and an iterative calculation sequence is necessary to numerically solve the steady-state population balance. The required calculation sequence is presented in Figure 3.
 
The sub-models are described in further detail below.
 
</hide><div class="user-show">
=== Breakage rates ===
</div><hide>
 
[[File:AGSAGVariableRates12.png|thumb|450px|Figure 4. Breakage rate distribution characterised by cubic spline interpolation.]]
 
{{Model theory (Text, AG/SAG Mill, Variable Rates, Breakage Rates)|4}}
 
</hide><div class="user-show">
 
=== Discharge rates ===
</div><hide>
 
The discharge rates (<math>D_i</math>) are related to the hold-up of slurry in the mill and particle classification at the discharge grates.
 
</hide><div class="user-show">
==== Slurry hold-up ====
</div><hide>
 
[[File:AGSAGVariableRates9.png|thumb|450px|Figure 5. Principal dimensions of an AG/SAG mill.]]
 
The volumetric flow rate of slurry discharged from a grated mill depends on the level of slurry hold-up within the mill, in a manner analogous to flow from the bottom of a filled tank.
 
In a steady-state model, the discharge flow rate is equal to the feed flow rate by definition. The following empirical relationship is used to estimate slurry hold-up in a grated mill for a given discharge flow rate:{{Napier-Munn et al. (1996)}}
 
:<math>L_{\rm V} = m_1 \left ( \dfrac{F}{V} \right )^{m_2}</math>
 
where:
* <math>L_{\rm V}</math> is the fraction of mill volume occupied by below grate size solids and water (v/v)
* <math>F</math> is the volumetric flow rate of slurry discharged from the mill (m<sup>3</sup>/min)
* <math>m_1</math> is a constant related to grate design and mill speed
* <math>m_2</math> is a constant assumed to take the value of 0.5.{{Kojovic et al. (2012)}}
 
The volume of the mill, <math>V</math>, is calculated as the sum of a cylinder and two right circular frustums:{{Gupta and Yan (2016)}}
 
:<math>V = \pi {R_{\rm m}}^2L + 2 \cdot \bigg[ \dfrac{\pi}{3} (R_{\rm m} - R_{\rm t}) \cdot \tan \alpha_{\rm c} \cdot \left ( {R_{\rm m}}^{2} + R_{\rm m} R_{\rm t} + {R_{\rm t}}^{2} \right) \bigg]</math>
 
where:
* <math>R_{\rm m}</math> is the radius of the mill inside the liners (m), equal to half of the diameter of the mill inside the liners, <math>D</math> (m)
* <math>R_{\rm t}</math> is the radius of the discharge trunnion (m), equal to half of the diameter of the discharge trunnion, <math>D_{\rm t}</math> (m)
* <math>L</math> is the length of the cylindrical (belly) section of the mill (m)
* <math>\alpha_{\rm c}</math> is the cone angle, measured as the angular displacement of the cone surface from the vertical direction (rad)
 
The principal dimensions of an AG/SAG mill required to compute mill volume and other properties are shown in Figure 5.
 
Morrell and Stephenson (1996) related discharge flow rate to slurry hold-up, grate design and mill speed with the following semi-empirical relation:{{Morrell and Stephenson (1996)}}
 
:<math>Q_{\rm m} = k_{\rm m} {J_{\rm pm}}^2 \gamma^{2.5} A \phi^{-1.34} D^{0.5}</math>
 
where
* <math>Q_{\rm m}</math> is the volumetric discharge rate of slurry through the grinding media zone  (m<sup>3</sup>/h)
* <math>k_{\rm m}</math> is the slurry discharge coefficient for the grinding media zone
* <math>J_{\rm pm}</math> is the net fractional slurry hold-up in the grinding media interstices (v/v)
* <math>A</math> is the total open area of grate apertures (m<sup>2</sup>)
* <math>\phi</math> is the fraction critical speed of the mill (frac)
* <math>D</math> is the mill diameter (m)
 
and the mean radial position of the grate apertures, <math>\gamma</math> (m/m), is defined as:
 
:<math>\gamma = \frac{\sum{r_ia_i}}{r_{\rm m} \sum{a_i}}</math>
 
where:
* <math>a_i</math> is the open area of all holes (m<sup>2</sup>) at radial position <math>r_i</math> (m)
* <math>r_{\rm m}</math> is the radius of the mill inside the liners (m)
 
In addition to fine slurry, particles up to the grate aperture size will also discharge from the mill. To estimate total discharge flow rate, <math>Q</math> (m<sup>3</sup>/h), Morrell and Stephenson (1996) suggest the following correction:{{Morrell and Stephenson (1996)}}
 
:<math>Q = k_{\rm g} Q_{\rm m}</math>
 
where <math>k_{\rm g}</math> is a factor to account for coarse material, and taking the values shown in Table 2.
 
:{| class="wikitable"
|+ Table 2. Applied values for <math>k_{\rm g}</math>.{{Morrell and Stephenson (1996)}}
|-
! Aperture !! <math>k_{\rm g}</math>
|-
| Grates only; <19mm || 1.07
|-
| Grates only; 19mm - 28mm|| 1.125
|-
| Grates >38mm or pebble ports || 1.2
|}
 
The value of <math>m_1</math> for a given grate design and mill can be determined by observing that <math>L_{\rm V} = J_{\rm pm}</math> and <math>F = Q \big / 60</math> in the above equations, i.e.:{{Kojovic et al. (2012)}}
 
:<math>m_1 \left ( \dfrac{Q}{60V} \right )^{0.5} = {k_{\rm g}}^{-0.5} {k_{\rm m}}^{-0.5}  Q^{0.5} \gamma^{-1.25} A^{-0.5} \phi^{0.67} D^{-0.25}</math>
 
The mill volume, <math>V</math>, can expressed as the product of the mill cross sectional area and an ''equivalent grinding length'', <math>L_{\rm eq}</math> (m), i.e.:
 
:<math>V = \pi \left ( \dfrac{D}{2} \right )^2 L_{\rm eq} \implies L_{\rm eq} = \dfrac{V}{\pi \left ( \frac{D}{2} \right )^2}</math>
 
Furthermore, the total open area of the grates, <math>A</math> (m<sup>2</sup>), can be replaced with an expression combining the grate ''open area fraction'',  <math>A_{\rm OF}</math> (m<sup>2</sup>/m<sup>2</sup>), and mill cross-sectional area:
 
:<math>A = \pi \left ( \dfrac{D}{2} \right )^2 A_{\rm OF}</math>
 
Replacing the <math>V</math> and <math>A</math> terms in the <math>m_1</math> equation above yields:
 
:<math>m_1 = \sqrt{60} \cdot ({k_{\rm g}} {k_{\rm m}})^{-0.5} \gamma^{-1.25} {A_{\rm OF}}^{-0.5} \phi^{0.67} D^{-0.25} {L_{\rm eq}}^{0.5}</math>
 
Thus, slurry hold-up, <math>L_{\rm V}</math>, can be computed for a given feed/discharge flow rate, grate design and mill.
 
</hide><div class="user-show">
==== Classification and discharge ====
</div><hide>
 
[[File:AGSAGVariableRates10.png|thumb|450px|Figure 6. Classification function, <math>C_i</math>, with pebble port open are fraction, <math>f_p</math>, specified.]]
 
[[File:AGSAGVariableRates11.png|thumb|450px|Figure 7. Classification function, <math>C_i</math>, where pebble port open are fraction, <math>f_p</math>, is zero, i.e grates only.]]
 
{{Model theory (Text, AG/SAG Mill, Variable Rates, Classification)}}
 
Figure 6 shows an example classification function with pebble ports included, whilst Figure 7 shows the same function with a grate-only mill.
 
The value of <math>d_{\rm max}</math> is adjusted during the calculation sequence (Figure 3) to ensure the fraction of solids less than <math>x_{\rm g}</math> plus water retained in the mill load computed by the perfect mixing population balance matches the slurry hold-up determined by the [[AG/SAG Mill (Variable Rates)#Slurry_flow|slurry flow]] calculations.
 
</hide><div class="user-show">
 
=== Appearance function ===
 
{{Model theory (Text, AG/SAG Mill, Variable Rates, Appearance Function)}}
 
=== Mill power ===
</div><hide>
 
The Variable Rates AG/SAG model includes an implementation of the [[Tumbling Mill (Power, Morrell Continuum)|Morrell Continuum]] tumbling mill power model. The predicted mill power draw is not utilised by the Variable Rates model formulation in any manner, and is provided for information only.
 
</hide><div class="user-show">
==== Charge properties ====
</div><hide>
 
The power draw prediction requires an estimate of <math>J_{\rm t}</math> (v/v), the fraction of mill volume occupied by the charge, which includes coarse ore, balls, slurry, and void spaces.
 
Morrell (1992) provides relations for the mass of coarse ore, slurried ore, water and balls in a mill.{{Morrell (1992)}} Converting from mass to fraction of mill volume, these relations are:
 
:<math>\frac{V_{\rm co}}{V} = (J_{\rm t} - J_{\rm B})(1 - \varepsilon), \quad \frac{V_{\rm so}}{V} = J_{\rm t} \varepsilon U S, \quad \frac{V_{\rm L}}{V} = J_{\rm t} \varepsilon U (1 - S), \quad \frac{V_{\rm B}}{V} = J_{\rm B} (1 - \varepsilon)</math>
 
where:
* <math>V_{\rm co}</math>, <math>V_{\rm so}</math>, <math>V_{\rm L}</math>, and <math>V_{\rm B}</math> are the volumes of coarse ore, slurried ore, liquids, and balls in the mill, respectively (m<sup>3</sup>)
* <math>S</math> is the volume fraction of solids in the mill discharge (v/v)
* <math>U</math> is the fraction of void space between the coarse ore particles and balls that is filled with slurry (v/v)
 
The total volume of ore in the mill, <math>V_{\rm o}</math> (m<sup>3</sup>), is computed by the perfect mixing model, i.e.:
 
:<math>V_{\rm o} = \sum_{i=1}^n s_i</math>
 
Subtracting the slurried ore component from the total ore volume, the coarse ore volume is:
 
:<math>\frac{V_{\rm co}}{V} = \frac{V_{\rm o}}{V} - \frac{V_{\rm so}}{V} \implies (J_{\rm t} - J_{\rm B})(1 - \varepsilon) = \frac{\sum_{i=1}^n s_i}{V} - J_{\rm t} \varepsilon U S</math>
 
and rearranging for <math>J_{\rm t}</math> yields:
 
:<math>J_{\rm t} = \dfrac{J_{\rm B} (\varepsilon - 1) - \frac{\sum_{i=1}^n s_i}{V}}{\varepsilon (1 - U S) - 1}</math>
 
The value of <math>U</math> in the above equation is unknown, and is itself a function of <math>J_{\rm t}</math>. To simplify the calculations, <math>J_{\rm t}</math> is estimated for a given mill load and discharge by assuming <math>U = 1</math>.
 
Having computed an estimate for <math>J_{\rm t}</math>, the value of <math>U</math> may be approximated by:
 
:<math>U = \dfrac{L_{\rm V}}{\varepsilon J_{\rm t}}</math>
 
and the apparent density of the charge, <math>\rho_{\rm c}</math>, is:{{Morrell (1996a)}}
 
:<math>\rho_{\rm c} = \frac{J_{\rm t} \rho_{\rm S} (1 - \varepsilon + \varepsilon U S) + J_{\rm B}( \rho_{\rm B} - \rho_{\rm S})(1 - \varepsilon) + J_{\rm t} \varepsilon U (1 - S)}{J_{\rm t}}, \quad U \leq 1</math>
 
</hide><div class="user-show">
==== Power draw ====
</div><hide>
 
:''Main article'': [[Tumbling Mill (Power, Morrell Continuum)]]
 
This implementation of the Variable Rates AG/SAG model applies Morrell's (1996) tumbling mill power draw equations for a grated mill which include terms for the conical end sections of the mill.{{Morrell (1996a)}}{{Bueno et al. (2013)}}
 
The values of <math>J_{\rm t}</math>, <math>U</math>, and <math>\rho_{\rm c}</math>, plus mill dimensions and rotational speed are inputs to the power draw estimation equations.
 
The equations return the following charge position and power draw results:
* The angular position of the charge shoulder, <math>\theta_{\rm S}</math> (rad)
* The angular position of the charge toe, <math>\theta_{\rm T}</math> (rad)
* The charge surface radius, <math>r_{\rm i}</math> (m)
* The no-load power of the mill, <math>P_{\rm NoLoad}</math> (kW)
* The net power of the mill, <math>P_{\rm Net}</math> (kW)
* The gross power of the mill, <math>P_{\rm Gross}</math> (kW)
 
The complete equations are excluded here for brevity and are available at the article link above.
 
</hide><div class="user-show">
=== Internal mesh series ===
</div><hide>
 
{{Model theory (Text, AG/SAG Mill, Variable Rates, Internal Mesh)}}
 
</hide><div class="user-show">
 
=== Multicomponent modelling ===
</div><hide>
 
{{Model theory (Text, AG/SAG Mill, Variable Rates, Multicomponent)}}
 
</hide><div class="user-show">
 
=== Additional notes ===
</div><hide>
 
</hide><div class="user-show">
==== Breakage rates and mill load ====
</div><hide>
 
An important, and potentially overlooked, limitation of the Variable Rates AG/SAG mill model is the insensitivity of the breakage rate relationships to mill load. Mill simulations should therefore use mill loads close or equal to the load observed during model fitting, or 25% for design activities.{{Bailey et al. (2009)}}
 
</hide><div class="user-show">
==== Slurry pool ====
</div><hide>
 
Various published descriptions of the Variable Rates AG/SAG mill suggest that slurry pooling phenomena are excluded from slurry hold-up and power draw estimations.{{Morrell and Morrison (1996)}}{{Kojovic et al. (2012)}}{{Bueno et al. (2013)}}
 
This implementation similarly excludes slurry pooling, and any model results returning values of <math>U > 1</math> should be inspected carefully.
</hide>


== Excel ==
== Excel ==
Line 13: Line 286:
The Variable Rates AG/SAG mill model may be invoked from the Excel formula bar with the following function call:
The Variable Rates AG/SAG mill model may be invoked from the Excel formula bar with the following function call:


<syntaxhighlight lang="vb">=mdUnit_AGSAG_VariableRates(Parameters as Range, Size as Range, MillNewFeed as Range, MillRecycleFeed as Range, OreSG as Range, BallSizing as Range, RSize as Range, RConst as Range, OreBreakageParams as Range)</syntaxhighlight>
<syntaxhighlight lang="vb">=mdUnit_AGSAG_VariableRates(Parameters as Range, Size as Range, MillNewFeed as Range, OreSG as Range, BallSizing as Range, RConst as Range, OreBreakageParams as Range, Optional MillRecycleFeed as Range = Nothing)</syntaxhighlight>


{{Excel (Text, Help, No Arguments)}}
{{Excel (Text, Help, No Arguments)}}
Line 21: Line 294:
{{Excel (Text, Inputs)}}
{{Excel (Text, Inputs)}}


:<math>Parameters=
:<math>\mathit{Parameters} =
\begin{bmatrix}
\begin{bmatrix}
D\text{ (m)}\\
D\text{ (m)}\\
Line 28: Line 301:
\alpha_{c}\text{ (deg.)}\\
\alpha_{c}\text{ (deg.)}\\
\phi\text{ (frac)}\\
\phi\text{ (frac)}\\
A\text{ (m}^{\text{2}}\text{)}\\
A_{\rm OF}\text{ (m}^{\text{2}}\text{)}\\
f_{\rm p}\text{ (m}^2\text{/m}^2\text{)}\\
f_{\rm p}\text{ (m}^2\text{/m}^2\text{)}\\
x_{\rm p}\text{ (mm)}\\
x_{\rm p}\text{ (mm)}\\
Line 34: Line 307:
x_{\rm m}\text{ (mm)}\\
x_{\rm m}\text{ (mm)}\\
\gamma\text{ (m/m)}\\
\gamma\text{ (m/m)}\\
k\text{ (-)}\\
k_{\rm m}\text{ (-)}\\
J_{\rm B}\text{ (v/v)}\\
J_{\rm B}\text{ (v/v)}\\
\rho_{\rm B}\text{ (t/m}^3\text{)}\\
\rho_{\rm B}\text{ (t/m}^3\text{)}\\
d_{\rm B}\text{ (mm)}\\
d_{\rm B,Top}\text{ (mm)}\\
(F_{80})_{\rm Ref}\text{ (mm)}\\
F_{80}\text{ (mm)}\\
(d_1)_{\rm Int}\text{ (mm)}\\
d_1\text{ (mm)}\\
\varepsilon\text{ (v/v)}\\
\varepsilon\text{ (v/v)}\\
(Q_{\rm M,F})_{\rm L}\text{ (t/h)}\\
(Q_{\rm M,F})_{\rm L}\text{ (t/h)}\\
\rho_{\rm L}\text{ (t/m}^{\text{3}}\text{)}\\
\rho_{\rm L}\text{ (t/m}^{\text{3}}\text{)}\\
p\\
u\\
q\\
v\\
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\;\;\;\;\;\;


Size = \begin{bmatrix}
\mathit{Size} = \begin{bmatrix}
d_{1}\text{ (mm)}\\  
\hat{d}_{1}\text{ (mm)}\\  
\vdots\\  
\vdots\\  
d_n\text{ (mm)}\\  
\hat{d}_r\text{ (mm)}\\  
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\;\;\;\;\;\;


MillNewFeed= \begin{bmatrix}
\mathit{MillNewFeed} = \begin{bmatrix}
(Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\  
(Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\  
\vdots & \ddots & \vdots\\  
\vdots & \ddots & \vdots\\  
(Q_{\rm M,F})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{nm}\text{ (t/h)}\\  
(Q_{\rm M,F})_{r1}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{rm}\text{ (t/h)}\\  
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\;\;\;\;\;\;


MillRecycleFeed= \begin{bmatrix}
\mathit{OreSG} = \begin{bmatrix}
(Q_{\rm M,R})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,R})_{1m}\text{ (t/h)}\\
(\rho_{\rm S})_{1}\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_{\rm S})_m\text{ (t/m}^\text{3}\text{)}\\  
\vdots & \ddots & \vdots\\
\end{bmatrix},\;\;\;\;\;\;
(Q_{\rm M,R})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,R})_{nm}\text{ (t/h)}\\  
</math>
\end{bmatrix}


</math>


:<math>
:<math>
OreSG= \begin{bmatrix}
\mathit{BallSizing} = \begin{bmatrix}
(\rho_{\rm S})_{1}\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_{\rm S})_m\text{ (t/m}^\text{3}\text{)}\\  
(d_{\rm B})_1 \text{ (mm)} & (\mathit{MF}_{\rm B})_1\text{ (}%\text{ w/w)}\\
\vdots& \vdots\\
(d_{\rm B})_s \text{ (mm)} & (\mathit{MF}_{\rm B})_s\text{ (}%\text{ w/w)}\\
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\;\;\;\;\;\;


BallSizing = \begin{bmatrix}
\mathit{RConst} = \begin{bmatrix}
(\mathit{MF}_{\rm B})_{d_{\rm B}/\sqrt{2}}\text{ (}%\text{ w/w)}\\
\mathit{RConst}_1 \text{ (} \ln \rm h^{-1} \text{)}\\  
(\mathit{MF}_{\rm B})_{d_{\rm B}/(2\sqrt{2}})\text{ (}%\text{ w/w)}\\
(\mathit{MF}_{\rm B})_{d_{\rm B}/(3\sqrt{2}})\text{ (}%\text{ w/w)}\\
(\mathit{MF}_{\rm B})_{d_{\rm B}/(4\sqrt{2}})\text{ (}%\text{ w/w)}\\
\end{bmatrix},\;\;\;\;\;\;
 
RSize= \begin{bmatrix}
d_{1}\text{ (mm)}\\  
\vdots\\  
\vdots\\  
d_{k}\text{ (mm)}\\  
\mathit{RConst}_5 \text{ (} \ln \rm h^{-1} \text{)}\\  
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\;\;\;\;\;\;


RConst= \begin{bmatrix}
\mathit{OreBreakageParams} =
RConst_1\\  
\begin{bmatrix}
\vdots\\  
A_1\text{ (}%\text{ w/w)} & \dots & A_m\text{ (}%\text{ w/w)}\\
RConst_k\\  
b_1 & \dots & b_m\\
\end{bmatrix}
(t_{\rm a})_1\text{ (}%\text{ w/w)} & \dots & (t_{\rm a})_m\text{ (}%\text{ w/w)}\\
</math>
\end{bmatrix},\quad


:<math>OreBreakageParams=
\mathit{MillRecycleFeed} = \begin{bmatrix}
\begin{bmatrix}
(Q_{\rm M,R})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,R})_{1m}\text{ (t/h)}\\  
A_1 & \dots & A_k\\
\vdots & \ddots & \vdots\\  
b_1 & \dots & b_k\\
(Q_{\rm M,R})_{r1}\text{ (t/h)} & \dots & (Q_{\rm M,R})_{rm}\text{ (t/h)}\\  
(t_{\rm a})_1 & \dots & (t_{\rm a})_k\\
\end{bmatrix}^*
\end{bmatrix}  
</math>
</math>


where:
where:
* <math>D</math> is the diameter of the mill inside the liners (m)
* <math>L</math> is the length of the belly section of the mill (m)
* <math>D_{\rm t}</math> is diameter of the discharge trunnion (m)
* <math>\alpha_{\rm c}</math> is angle between the cone end surface and the vertical direction (deg)
* <math>\phi</math> is the fraction critical speed of the mill (frac)
* <math>A</math> is the open area fraction of the discharge grate (frac)
* <math>f_{\rm p}</math> is the pebble port area fraction (frac)
* <math>x_{\rm p}</math> is the size of the pebble port aperture (mm)
* <math>x_{\rm g}</math> is the size of the grate aperture (mm)
* <math>x_{\rm m}</math> is the fine size (mm)
* <math>\gamma</math> is the mean radial position of the grate apertures (m/m)
* <math>k</math> is the slurry discharge coefficient
* <math>J_{\rm B}</math> is the ball load volume fraction (v/v)
* <math>\rho_{\rm B}</math> is the density or specific gravity of the ball media (t/m<sup>3</sup> or -)
* <math>d_{\rm B}</math> is ball top size (mm)
* <math>(F_{80})_{\rm Ref}</math> is the reference ''F<sub>80</sub>'' size (mm)
* <math>(d_1)_{\rm Int}</math> is the internal mesh top size (mm)
* <math>\varepsilon</math> is the charge void fraction (v/v)
* <math>(Q_{\rm M,F})_{\rm L}</math> is the mass flow feed rate of liquids into the mill (t/h)
* <math>(Q_{\rm M,F})_{\rm L}</math> is the mass flow feed rate of liquids into the mill (t/h)
* <math>\rho_{\rm L}</math> is the Specific Gravity or density of liquids in the feed (- or t/m<sup>3</sup>)
* <math>\rho_{\rm L}</math> is the Specific Gravity or density of liquids in the feed (- or t/m<sup>3</sup>)
* <math>p</math> is an index of the Appearance function to view in the results
* <math>u</math> is an index of the Appearance function to view in the results
* <math>q</math> is an index of the Appearance function to view in the results
* <math>v</math> is an index of the Appearance function to view in the results
* <math>n</math> is the number of intervals
* <math>m</math> is the number of ore types
* <math>m</math> is the number of ore types
* <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm)
* <math>r</math> is the number of intervals of the external mesh series
* <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm)
* <math>s</math> is the number of intervals of the ball mesh series below the top size, including the submesh
* <math>Q_{\rm M,F}</math> is new feed mass flow rate (t/h)
* <math>\hat{d}_i</math> is the size of the external square mesh interval that feed mass is retained on (mm)
* <math>Q_{\rm M,R}</math> is recycle feed mass flow rate (t/h)
* <math>\hat{d}_{i+1}<\hat{d}_i<\hat{d}_{i-1}</math>, i.e. descending size order from top size (<math>\hat{d}_{1}</math>) to sub mesh (<math>\hat{d}_{p}=0</math>)
* <math>\rho_{\rm S}</math> is the density or specific gravity of solids (t/m<sup>3</sup> or -)
* <math>(d_{\rm B})_i</math> is the size of the square mesh interval that balls are retained on (mm)
* <math>\mathit{MF}_{\rm B}</math> is the mass fraction retained of balls (% w/w)
* <math>(\mathit{MF}_{\rm B})_i</math> is the mass fraction of balls retained on ball mesh series interval <math>i</math> (% w/w)
* <math>k</math> is the number of breakage rate knots
* <math>^*</math> indicates the <math>\mathit{MillRecycleFeed}</math> array is an optional input parameter, and is set to null if omitted
* <math>RConst</math> is a breakage rate constant
* <math>A</math> (%), <math>b</math>, and <math>t_{\rm a}</math> are ore breakage parameters


=== Results ===
=== Results ===
Line 146: Line 390:
\text{Iterations}\\
\text{Iterations}\\
\text{Iteration error}\\
\text{Iteration error}\\
\text{Mill volume (m}^{\text{3}}\text{)}\\
V\text{ (m}^{\text{3}}\text{)}\\
\text{Mill speed (rpm)}\\
\text{Mill speed (rpm)}\\
Q_{\rm V,F}\\
Q_{\rm V,F}\\
Line 158: Line 402:
m_1\text{ (-)}\\
m_1\text{ (-)}\\
m_2\text{ (-)}\\
m_2\text{ (-)}\\
d_{\rm Max}\text{ (h}^{-1}\text{)}\\
d_{\rm max}\text{ (h}^{-1}\text{)}\\
S_{20}\text{ (mm)}\\
S_{20}\text{ (mm)}\\
\mathit{EL}\text{ (kWh)}\\
E_q\text{ (kWh)}\\
\rho_{\rm c}\text{ (t/m}^3\text{)}\\
\rho_{\rm c}\text{ (t/m}^3\text{)}\\
\theta_{\rm S}\text{ (rad)}\\
\theta_{\rm S}\text{ (rad)}\\
Line 175: Line 419:


\begin{bmatrix}
\begin{bmatrix}
d_1\text{ (mm)}\\
\hat{d}_1\text{ (mm)}\\
\vdots\\
\vdots\\
d_n\text{ (mm)}
\hat{d}_q\text{ (mm)}
\end{bmatrix}
\end{bmatrix}


Line 185: Line 429:
(Q_{\rm M,P})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,P})_{1m}\text{ (t/h)}\\
(Q_{\rm M,P})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,P})_{1m}\text{ (t/h)}\\
\vdots & \ddots & \vdots\\
\vdots & \ddots & \vdots\\
(Q_{\rm M,P})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,P})_{nm}\text{ (t/h)}\\
(Q_{\rm M,P})_{q1}\text{ (t/h)} & \dots & (Q_{\rm M,P})_{qm}\text{ (t/h)}\\
\end{bmatrix}
\end{bmatrix}


Line 191: Line 435:


\begin{bmatrix}
\begin{bmatrix}
(M_{\rm S})_{11}\text{ (t/h)} & \dots & (M_{\rm S})_{1m}\text{ (t/h)}\\
(M_{\rm S})_{11}\text{ (t)} & \dots & (M_{\rm S})_{1m}\text{ (t)}\\
\vdots & \ddots & \vdots\\
\vdots & \ddots & \vdots\\
(M_{\rm S})_{n1}\text{ (t/h)} & \dots & (M_{\rm S})_{nm}\text{ (t/h)}\\
(M_{\rm S})_{q1}\text{ (t)} & \dots & (M_{\rm S})_{qm}\text{ (t)}\\
\end{bmatrix}
\end{bmatrix}


Line 201: Line 445:
d_1\text{ (mm)}\\
d_1\text{ (mm)}\\
\vdots\\
\vdots\\
d_{31}\text{ (mm)}
d_n\text{ (mm)}
\end{bmatrix}
\end{bmatrix}


Line 208: Line 452:
\bar{d}_1\text{ (mm)}\\
\bar{d}_1\text{ (mm)}\\
\vdots\\
\vdots\\
\bar{d}_{31}\text{ (mm)}\\
\bar{d}_n\text{ (mm)}\\
\end{bmatrix}
\end{bmatrix}


Line 216: Line 460:
D_{1}\left(\text{h}^\text{-1}\right)\\
D_{1}\left(\text{h}^\text{-1}\right)\\
\vdots\\
\vdots\\
D_{31}\left(\text{h}^\text{-1}\right)\\
D_n\left(\text{h}^\text{-1}\right)\\
\end{bmatrix}
\end{bmatrix}


Line 224: Line 468:
R_{1}\left(\text{h}^\text{-1}\right)\\
R_{1}\left(\text{h}^\text{-1}\right)\\
\vdots\\
\vdots\\
R_{31}\left(\text{h}^\text{-1}\right)\\
R_n\left(\text{h}^\text{-1}\right)\\
\end{bmatrix}
\end{bmatrix}


Line 232: Line 476:
(E_{\rm cs})_{1}\text{ (kWh/t)}\\
(E_{\rm cs})_{1}\text{ (kWh/t)}\\
\vdots\\
\vdots\\
(E_{\rm cs})_{31}\text{ (kWh/t)}\\
(E_{\rm cs})_n\text{ (kWh/t)}\\
\end{bmatrix}
\end{bmatrix}


Line 238: Line 482:


\begin{bmatrix}
\begin{bmatrix}
A_{p,1}\text{ (frac)}\\
A_{u1}\text{ (frac)}\\
\vdots\\
\vdots\\
A_{p,31}\text{ (frac)}\\
A_{un}\text{ (frac)}\\
\end{bmatrix}
\end{bmatrix}


Line 246: Line 490:


\begin{bmatrix}
\begin{bmatrix}
A_{q,1}\text{ (frac)}\\
A_{v1}\text{ (frac)}\\
\vdots\\
\vdots\\
A_{q,31}\text{ (frac)}\\
A_{vn}\text{ (frac)}\\
\end{bmatrix}\\
\end{bmatrix}\\


Line 283: Line 527:
* <math>\text{Iteration error}</math> is the numerical error of the converged load approximation
* <math>\text{Iteration error}</math> is the numerical error of the converged load approximation
* <math>Q_{\rm V,F}</math> is the flow rate of pulp into the mill (m<sup>3</sup>/h)
* <math>Q_{\rm V,F}</math> is the flow rate of pulp into the mill (m<sup>3</sup>/h)
* <math>\text{Mill volume}</math> is the total volume inside the mill, calculated as the sum of a cylinder and two frustums (m<sup>3</sup>)
* <math>\text{Mill speed}</math> is the [[Tumbling Mill (Speed)|rotational rate of the mill]] (rpm)
* <math>\text{Mill speed}</math> is the [[Tumbling Mill (Speed)|rotational rate of the mill]] (rpm)
* <math>M_{\rm S}</math> is the mass of ore solids in the mill (t)
* <math>M_{\rm S}</math> is the mass of ore solids in the mill (t)
Line 289: Line 532:
* <math>M_{\rm B}</math> is the mass of balls in the mill (t)
* <math>M_{\rm B}</math> is the mass of balls in the mill (t)
* <math>M</math> is the total mass of ore, liquids and balls in the mill (t)
* <math>M</math> is the total mass of ore, liquids and balls in the mill (t)
* <math>J_{\rm t}</math> is the charge volume fraction (v/v)
* <math>U</math> is the void fill fraction (v/v)
* <math>k_{\rm g}</math> is the coarse factor (-)
* <math>m_1</math> is a parameter of the Austin mill holdup equation
* <math>m_2</math> is a parameter of the Austin mill holdup equation
* <math>d_{\rm Max}</math> is maximum discharge rate from the mill (h<sup>-1</sup>)
* <math>S_{20}</math> is the geometric mean size of the top 20% of the load (mm)
* <math>\mathit{EL}</math> is the energy level in the mill (kWh)
* <math>\rho_{\rm c}</math> is the charge density (t/m<sup>3</sup>)
* <math>\theta_{\rm S}</math> is angular position of the charge shoulder (rad)
* <math>\theta_{\rm T}</math> is angular position of the charge toe (rad)
* <math>r_{\rm i}</math> is the charge surface radius (m)
* <math>P_{\rm NoLoad}</math> is the no-load power of the mill (kW)
* <math>P_{\rm Net}</math> is the net power of the mill (kW)
* <math>P_{\rm Gross}</math> is the gross power of the mill (kW)
* <math>Q_{\rm M,P}</math> is product mass flow rate (t/h)
* <math>Q_{\rm M,P}</math> is product mass flow rate (t/h)
* <math>\bar{d}_i</math> is the [[Conversions|geometric mean size]] of the internal mesh series interval that mass is retained on (mm)
* <math>\bar{d}_i</math> is the [[Conversions|geometric mean size]] of the internal mesh series interval that mass is retained on (mm)
* <math>D</math> is the discharge rate (h<sup>-1</sup>)
* <math>R</math> is the breakage rate (h<sup>-1</sup>)
* <math>E_{\rm cs}</math> is specific comminution energy (kWh/t)
* <math>A</math> is the Appearance function (frac)


=== Example ===
=== Example ===
Line 317: Line 541:
{|  
{|  
|- style="vertical-align:top;"
|- style="vertical-align:top;"
| [[File:AGSAGVariableRates1.png|left|frame|Figure 1. Example showing the selection of the '''Parameters''' (blue frame) array in Excel.]]  
| [[File:AGSAGVariableRates1.png|left|frame|Figure 8. Example showing the selection of the '''Parameters''' (blue frame) array in Excel.]]  
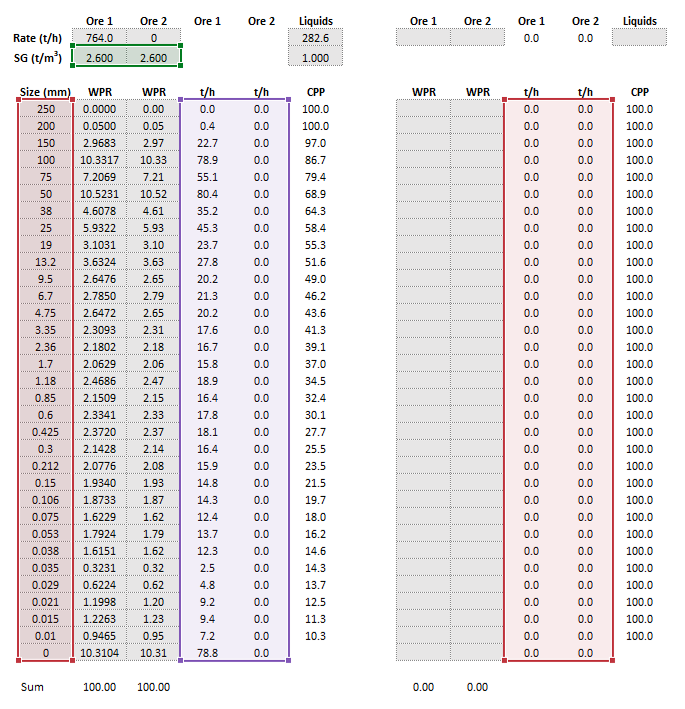
| [[File:AGSAGVariableRates2.png|left|frame|Figure 2. Example showing the selection of the '''Size''' (red frame), '''OreSG''' (pink frame), '''MillNewFeed''' (purple frame) and '''MillRecycleFeed''' (green frame) arrays in Excel.]]  
| [[File:AGSAGVariableRates2.png|left|frame|Figure 9. Example showing the selection of the '''Size''' (dark red frame), '''OreSG''' (green frame), '''MillNewFeed''' (purple frame) and '''MillRecycleFeed''' (light red frame) arrays in Excel.]]  
|}
|}
{|  
{|  
|- style="vertical-align:top;"
|- style="vertical-align:top;"
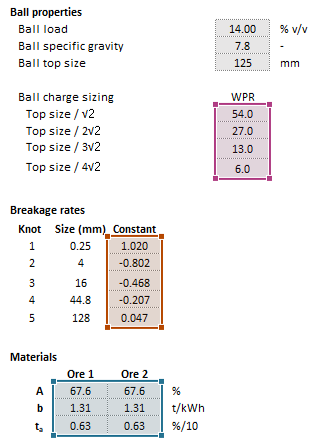
| [[File:AGSAGVariableRates3.png|left|frame|Figure 3. Example showing the selection of the '''BallSizing''' (brown frame), '''RSize''' (teal frame), '''RConst''' (blue frame), and '''OreBreakageParams''' (red frame) arrays in Excel.]]  
| [[File:AGSAGVariableRates3.png|left|frame|Figure 10. Example showing the selection of the '''BallSizing''' (purple frame), '''RConst''' (brown frame), and '''OreBreakageParams''' (teal frame) arrays in Excel.]]  
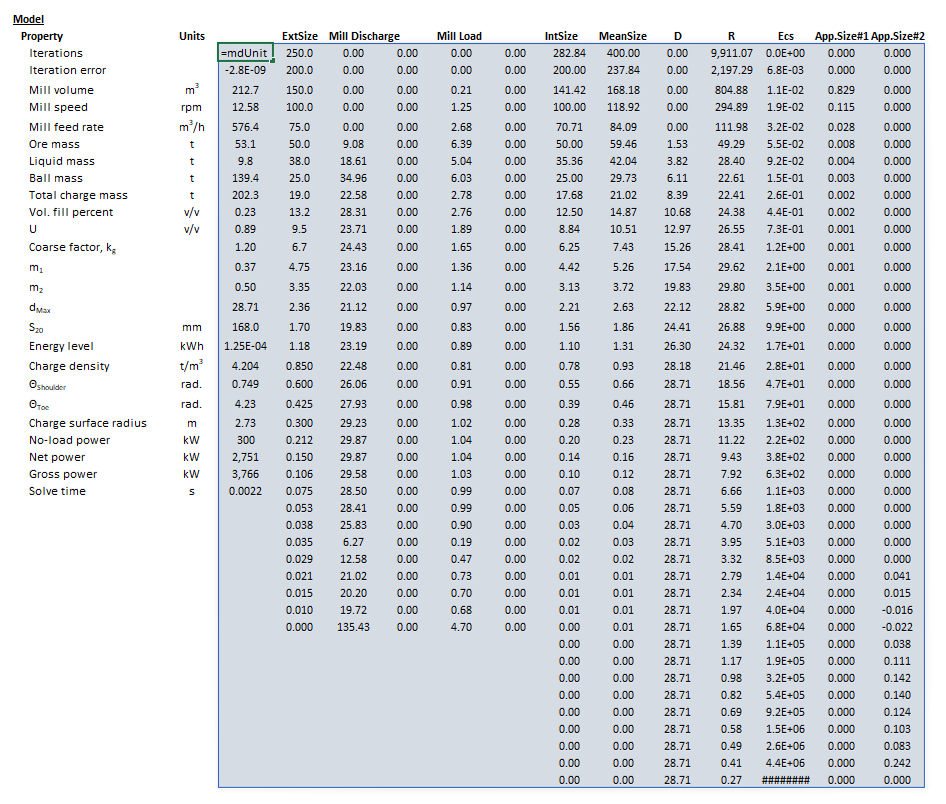
| [[File:AGSAGVariableRates4.png|left|frame|Figure 8. Example showing the outline of the '''Results''' (light blue frame) array in Excel.]]
| [[File:AGSAGVariableRates4.png|left|frame|Figure 11. Example showing the outline of the '''Results''' (light blue frame) array in Excel.]]
|}
|}


Line 332: Line 556:
{{SysCAD (Page, Mill, DLL*Mill)|PowerModels=true|MediaTraj=true|MediaStrings=true}}
{{SysCAD (Page, Mill, DLL*Mill)|PowerModels=true|MediaTraj=true|MediaStrings=true}}


==== Mill page ====
{{SysCAD (Page, AG/SAG Mill, Variable Rates, Mill)}}
 
The Mill page is used to specify the input parameters for the mill model.
 
{{SysCAD_Table_Header}}
 
|-
! colspan="3" style="text-align:left;" |''VariableRates''
 
{{SysCAD (Text, Help Link)}}
 
|-
! colspan="3" style="text-align:left;" |''Requirements''
{{SysCAD (Text, NumParallelUnits)}}
|-
! colspan="3" style="text-align:left;" |''Mill''
|-
|Diameter
|Input
|The inside liner diameter of the mill.
|-
|BellyLength
|Input
|The inside liner belly length of the mill, excluding cones.
|-
|TrunnionDiameter
|Input
|The inside liner trunnion diameter of the mill.
|-
|ConeAngle
|Input
|Angle of the feed and discharge end cones, measured as positive displacement from the vertical direction.
|-
|FracCS
|Input
|The fraction critical speed of the mill.
|-
! colspan="3" style="text-align:left;" |''Grate''
|-
|OpenAreaFrac
|Input
|Open area fraction of the grate.
|-
|PebblePortFrac / fp
|Input
|Pebble port area fraction.
|-
|PebblePortAperture / xp
|Input
|Pebble port aperture size.
|-
|GrateAperture / xg
|Input
|Grate aperture size.
|-
|FineSize / xm
|Input
|Fine size, size at which particles behave like water.
|-
|MeanRadialPosition / gamma
|Input
|Mean radial position of the grate apertures.
|-
|SlurryDischCoeff / k
|Input
|Slurry discharge coefficient.
|-
! colspan="3" style="text-align:left;" |''Ball''
|-
|BallLoad
|Input
|Ball load fraction.
|-
|BallSG
|Input
|Density (Specific Gravity) of ball media.
|-
|BallTopSize
|Input
|Top size of new ball media.
|-
|Size
|style="background: #eaecf0" | Display
|Ball sizing intervals.
|-
|Load
|style="background: #eaecf0" | Display
|Mass fraction retained of ball media in each ball sizing interval.
|-
! colspan="3" style="text-align:left;" |''RFunction''
|-
|Size
|Input
|Spline knot size positions.
|-
| Ln(R)
|Input
|Values of <math>\ln R</math>  at each spline knot position.
|-
! colspan="3" style="text-align:left;" |''Other''
|-
|ReferenceF80
|Input
|Reference F80 size.
|-
|InternalMeshTopSize
|Input
|Top size of internal mesh series.
|-
|Voidage
|Input
|Volumetric fraction of void space in charge.
|-
|NetPowerAdjust
|Input
|Net Power Adjust factor of mill power equation.
|}
 
==== Ore page ====
 
This page is used to define the comminution properties of SysCAD species with the size distribution quality in the project.
 
{{SysCAD_Table_Header}}
 
|-
! colspan="3" style="text-align:left;" |''Ore''
|- style="vertical-align:top;"
|OreSpecific
|CheckBox
|
* Ore-specific parameters, allows the ore breakage parameters to be separately input for all species.
* Default is all species have the same set of single input properties.
* This option is only available if there is more than one species in the project with the size distribution property.
|-
|A
|Input / Display
|Impact ore breakage parameter.
|-
|b
|Input / Display
|Impact ore breakage parameter.
|-
|ta
|Input / Display
|Abrasion ore breakage parameter.
|-
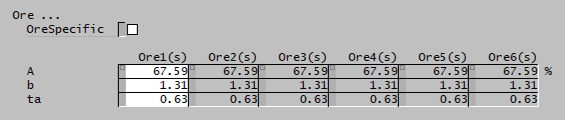
|colspan="3" | [[File:AGSAGVariableRates5.png]] [[File:AGSAGVariableRates6.png]]
|}
 
==== Results page ====
 
This page is used to display the model results.
 
{{SysCAD_Table_Header}}
 
|-
! colspan="3" style="text-align:left;" |''Results''
|-
! colspan="3" style="text-align:left;" |''Solver''
|-
|Iterations
|style="background: #eaecf0" | Display
|Number of iterations to converge internal load solver.
|-
|IterationError
|style="background: #eaecf0" | Display
|Numerical approximation error of internal load solver.
|-
! colspan="3" style="text-align:left;" |''Mill Properties''
|-
|MillVolume
|style="background: #eaecf0" | Display
|Internal volume of the mill.
|-
|MillSpeed
|style="background: #eaecf0" | Display
|Rotational speed of the mill.
|-
|MillFeedRate / Feed.SLQv
|style="background: #eaecf0" | Display
|Volumetric feed rate of pulp into the mill.
|-
! colspan="3" style="text-align:left;" |''Mill Contents''
|-
|OreMass
|style="background: #eaecf0" | Display
|Mass of ore (solids with PSD) in the mill.
|-
|LiquidMass
|style="background: #eaecf0" | Display
|Mass of liquids in the mill.
|-
|BallMass
|style="background: #eaecf0" | Display
|Mass of ball media in the mill.
|-
|TotalChargeMass
|style="background: #eaecf0" | Display
|Total mass of ore, liquids and balls in the mill.
|-
|VolTotalLoad
|style="background: #eaecf0" | Display
|Volumetric fraction of mill volume of total charge (ore, liquids, balls and void space).
|-
! colspan="3" style="text-align:left;" |''Mill Discharge''
|-
|m1
|style="background: #eaecf0" | Display
|Parameter of the Austin mill holdup relationship.
|-
|m2
|style="background: #eaecf0" | Display
|Parameter of the Austin mill holdup relationship.
|-
|dMax
|style="background: #eaecf0" | Display
|Maximum discharge rate of load volume through the grate.
|-
! colspan="3" style="text-align:left;" |''Charge Properties''
|-
|S20
|style="background: #eaecf0" | Display
|Size of the top (largest) 20% of the load.
|-
|ChargeDensity
|style="background: #eaecf0" | Display
|Density of the charge.
|-
|U
|style="background: #eaecf0" | Display
|Fraction of charge void space filled with slurry.
|-
|ThetaShoulder
|style="background: #eaecf0" | Display
|Angular position of the charge shoulder.
|-
|ThetaTue
|style="background: #eaecf0" | Display
|Angular position of the charge toe.
|-
|ChargeSurfaceRadius
|style="background: #eaecf0" | Display
|Radius of the inner charge surface.
|-
! colspan="3" style="text-align:left;" |''Power''
|-
|NoLoadPower
|style="background: #eaecf0" | Display
|No-load power draw of the mill.
|-
|NetPower
|style="background: #eaecf0" | Display
|Net power draw of the mill.
|-
|GrossPower
|style="background: #eaecf0" | Display
|Gross power draw of the mill.
|}


==== RiDi page ====
{{SysCAD (Page, AG/SAG Mill, Variable Rates, Ore)}}


This page displays the breakage and discharge rates for each size interval computed by the model.
{{SysCAD (Page, AG/SAG Mill, Variable Rates, Results)|Steady-state=true}}


{{SysCAD_Table_Header}}
{{SysCAD (Page, AG/SAGMill, Variable Rates, Ri/Di)}}
 
|-
! colspan="3" style="text-align:left;" |''Rates''
|-
|Size
|style="background: #eaecf0" | Display
|Size of each interval in internal mesh series.
|-
|MeanSize
|style="background: #eaecf0" | Display
|Geometric mean size of each interval in internal mesh series.
|-
| R
|style="background: #eaecf0" | Display
| Value of breakage rate, <math>R_i</math>, for each size interval, for each ore species.
|-
| D
|style="background: #eaecf0"; | Display
| Value of discharge rate, <math>D_i</math>, for each size interval.
|-
| Ecs
|style="background: #eaecf0"; | Display
| Value of the specific comminution energy for each size interval.
|}


==== Load page ====
{{SysCAD (Page, AG/SAGMill, Variable Rates, Load)}}


This page displays information about the balls, solids and liquids that currently comprise the mill load.
{{SysCAD (Page, Tumbling Mill, Power)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill|HF=true|MorrellC=true|MorrellE=true|MorrellD=true|HildenPowell=true}}


{{SysCAD_Table_Header}}
{{SysCAD (Page, Tumbling Mill, MediaStrings)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill}}


{{SysCAD (Text, Distribution)}}
{{SysCAD (Page, Tumbling Mill, MediaTraj)|modelpage={{SysCAD (Text, UnitType Prefix)}}Mill}}


|-
{{SysCAD (Page, About)}}
! colspan="3" style="text-align:left;" |''Load''
|-
|SolidMass / SMt
|style="background: #eaecf0" | Display
|The mass of solids with the SysCAD size distribution property currently in the mill.
|-
|LiquidMass / LMt
|style="background: #eaecf0" | Display
|The mass of liquids plus solids without the SysCAD size distribution property currently in the mill.
|-
|BallMass / BMt
|style="background: #eaecf0" | Display
|The mass of ball media in the mill.
|-
|Size
|style="background: #eaecf0" | Display
|Size of each interval in the external mesh series.
|-
|MeanSize
|style="background: #eaecf0" | Display
|Geometric mean size of each interval in the external mesh series.
|-
|Load
|style="background: #eaecf0" | Display
|The mass of solids with the SysCAD size distribution property currently in the mill, by size and species.
|}


{{SysCAD (Page, Tumbling Mill, Power)|modelpage={{Name (Text, Company Name)|nospace=1}}*Mill|HF=true|MorrellC=true|MorrellE=true|MorrellD=true|HildenPowell=true}}
== See also ==


{{SysCAD (Page, Tumbling Mill, MediaStrings)|modelpage={{Name (Text, Company Name)|nospace=1}}*Mill}}
* [[AG/SAG Mill (Variable Rates, Dynamic)]]


{{SysCAD (Page, Tumbling Mill, MediaTraj)|modelpage={{Name (Text, Company Name)|nospace=1}}*Mill}}
== External links ==


{{SysCAD (Page, About)}}
* [https://help.syscad.net/Met_Dynamics_-_Mill Met Dynamics - Mill (help.syscad.net)]
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Crushing_and_Grinding_Example Crushing and Grinding Example project (help.syscad.net)]
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Crushing,_Grinding_and_Flotation_Example Crushing, Grinding, and Flotation Example project (help.syscad.net)]


== References ==
== References ==

Latest revision as of 09:20, 9 July 2025

Description

This article describes an implementation of the Autogenous (AG) and Semi-Autogenous (SAG) mill model originated by Leung (1987) and extended with variable breakage rates by Morrell and Morrison (1996).[1][2][3]

The formulation is referred to in the associated literature as the "Variable Rates" model (Morrell et al., 2001).[4]

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Calculation sequence

Breakage rates

Discharge rates

Slurry hold-up

Classification and discharge

Appearance function

High energy

Ball load

Low energy

Combined appearance function

Mill power

Charge properties

Power draw

Internal mesh series

Multicomponent modelling

Additional notes

Breakage rates and mill load

Slurry pool

Excel

The Variable Rates AG/SAG mill model may be invoked from the Excel formula bar with the following function call: 

=mdUnit_AGSAG_VariableRates(Parameters as Range, Size as Range, MillNewFeed as Range, OreSG as Range, BallSizing as Range, RConst as Range, OreBreakageParams as Range, Optional MillRecycleFeed as Range = Nothing)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

Inputs

The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:


where:

  • is the mass flow feed rate of liquids into the mill (t/h)
  • is the Specific Gravity or density of liquids in the feed (- or t/m3)
  • is an index of the Appearance function to view in the results
  • is an index of the Appearance function to view in the results
  • is the number of ore types
  • is the number of intervals of the external mesh series
  • is the number of intervals of the ball mesh series below the top size, including the submesh
  • is the size of the external square mesh interval that feed mass is retained on (mm)
  • , i.e. descending size order from top size () to sub mesh ()
  • is the size of the square mesh interval that balls are retained on (mm)
  • is the mass fraction of balls retained on ball mesh series interval (% w/w)
  • indicates the array is an optional input parameter, and is set to null if omitted

Results

The results are displayed in Excel as an array corresponding to the matrix notation below:

where:

  • is the number of internal computation steps required to converge the load
  • is the numerical error of the converged load approximation
  • is the flow rate of pulp into the mill (m3/h)
  • is the rotational rate of the mill (rpm)
  • is the mass of ore solids in the mill (t)
  • is the mass of liquids in the mill (t)
  • is the mass of balls in the mill (t)
  • is the total mass of ore, liquids and balls in the mill (t)
  • is product mass flow rate (t/h)
  • is the geometric mean size of the internal mesh series interval that mass is retained on (mm)

Example

The images below show the selection of input arrays and output results in the Excel interface.

Figure 8. Example showing the selection of the Parameters (blue frame) array in Excel.
Figure 9. Example showing the selection of the Size (dark red frame), OreSG (green frame), MillNewFeed (purple frame) and MillRecycleFeed (light red frame) arrays in Excel.
Figure 10. Example showing the selection of the BallSizing (purple frame), RConst (brown frame), and OreBreakageParams (teal frame) arrays in Excel.
Figure 11. Example showing the outline of the Results (light blue frame) array in Excel.

SysCAD

The sections and variable names used in the SysCAD interface are described in detail in the following tables.

MD_Mill page

The first tab page in the access window will have this name.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Tag Display This name tag may be modified with the change tag option.
Condition Display OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount Display The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc Display This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.

If this field is blank, then SysCAD will display the unit class ID.

Requirements
On CheckBox This enables the unit. If this box is not checked, then the material will pass straight through the mill with no change to the size distribution.
NumParallelUnits Input The number of parallel, identical units to simulate:
  • Feed is divided by the number of parallel units before being sent to the unit model.
  • Unit model product is multiplied back by the same value and returned to the SysCAD product stream.
  • All unit model result values are shown per parallel unit.
Method Fixed Discharge The discharge particle size distribution is user defined. Different distributions can be used for different solids.
AG/SAG (Variable Rates) The Variable Rates AG/SAG mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids.
Rod Mill (Lynch) The Lynch rod mill model is used to determine the mill product size distribution. Different parameters can be used for different solids.
Ball (Perfect Mixing) The Perfect Mixing ball mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids.
Stirred (Perfect Mixing) The Perfect Mixing stirred mill model (steady-state or dynamic) is used to determine the mill product size distribution. Different parameters can be used for different solids.
Mill (Herbst-Fuerstenau) The Herbst-Fuerstenau model is used to determine the mill product size distribution. Different parameters can be used for different solids.
PowerModels CheckBox Show alternative mill power model calculations on the Power page.
MediaTrajectory CheckBox Show mill media rolling, sliding and free flight trajectory computations on the MediaTraj page.
MediaStrings CheckBox Show media size distributions at recharge equilibrium on the MediaStrings page.
Options
ShowQFeed CheckBox QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream.
ShowQProd CheckBox QProd and associated tab pages (eg Sp) will become visible, showing the properties of the products.
SizeForPassingFracCalc Input Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section.
FracForPassingSizeCalc Input Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section.
Stream Summary
MassFlow / Qm Display The total mass flow in each stream.
SolidMassFlow / SQm Display The Solids mass flow in each stream.
LiquidMassFlow / LQm Display The Liquid mass flow in each stream.
VolFlow / Qv Display The total Volume flow in each stream.
Temperature / T Display The Temperature of each stream.
Density / Rho Display The Density of each stream.
SolidFrac / Sf Display The Solid Fraction in each stream.
LiquidFrac / Lf Display The Liquid Fraction in each stream.
Passing Display The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream.
Passes Display The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction.

Mill page

The Mill page is used to specify the input parameters for the mill model.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
VariableRates
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
Mill
Diameter Input The inside liner diameter of the mill.
BellyLength Input The inside liner belly length of the mill, excluding cones.
TrunnionDiameter Input The inside liner trunnion diameter of the mill.
ConeAngle Input Angle of the feed and discharge end cones, measured as positive displacement from the vertical direction.
FracCS Input The fraction critical speed of the mill.
Grate
OpenAreaFrac Input Open area fraction of the grate.
PebblePortFrac / fp Input Pebble port area fraction.
PebblePortAperture / xp Input Pebble port aperture size.
GrateAperture / xg Input Grate aperture size.
FineSize / xm Input Fine size, size at which particles behave like water.
MeanRadialPosition / gamma Input Mean radial position of the grate apertures.
SlurryDischCoeff / k Input Slurry discharge coefficient.
Ball
BallLoad Input Ball load fraction.
BallSG Input Density (Specific Gravity) of ball media.
NumBallMeshSizes Input Number of ball mesh sizes below the top size, including the submesh.
BallTopSize Input Top size of new ball media.
Size Input / Display Ball sizing intervals.
Load Input Mass fraction retained of ball media in each ball sizing interval.
RFunction
RSize Display Spline knot positions.
RConst Input Values of at each spline knot position.
Other
ReferenceF80 Input Reference F80 size.
InternalMeshTopSize Input Top size of internal mesh series.
Voidage Input Volumetric fraction of void space in charge.
NetPowerAdjust Input Net Power Adjust factor of mill power equation.

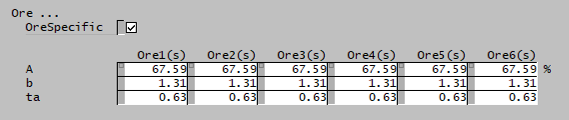
Ore page

This page is used to define the comminution properties of SysCAD species with the size distribution quality in the project.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Ore
OreSpecific CheckBox
  • Ore-specific parameters, allows the ore breakage parameters to be separately input for all species.
  • Default is all species have the same set of single input properties.
  • This option is only available if there is more than one species in the project with the size distribution property.
A Input / Display Impact ore breakage parameter.
b Input / Display Impact ore breakage parameter.
ta Input / Display Abrasion ore breakage parameter.
AGSAGVariableRates5.png AGSAGVariableRates6.png

Results page

This page is used to display the model results.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Results
Solver
Iterations Display Number of iterations to converge internal load solver.
IterationError Display Numerical approximation error of internal load solver.
Mill Properties
MillVolume Display Internal volume of the mill.
MillSpeed Display Rotational speed of the mill.
MillFeedRate / Feed.SLQv Display Volumetric feed rate of pulp into the mill.
Mill Contents
OreMass Display Mass of ore (solids with PSD) in the mill.
LiquidMass Display Mass of liquids in the mill.
BallMass Display Mass of ball media in the mill.
TotalChargeMass Display Total mass of ore, liquids and balls in the mill.
VolTotalLoad Display Volumetric fraction of mill volume of total charge (ore, liquids, balls and void space).
Mill Discharge
m1 Display Parameter of the Austin mill holdup relationship.
m2 Display Parameter of the Austin mill holdup relationship.
dMax Display Maximum discharge rate of load volume through the grate.
Charge Properties
S20 Display Size of the top (largest) 20% of the load.
ChargeDensity Display Density of the charge.
U Display Fraction of charge void space filled with slurry.
ThetaShoulder Display Angular position of the charge shoulder.
ThetaToe Display Angular position of the charge toe.
ChargeSurfaceRadius Display Radius of the inner charge surface.
Power
NoLoadPower Display No-load power draw of the mill.
NetPower Display Net power draw of the mill.
GrossPower Display Gross power draw of the mill.

RiDi page

This page displays the breakage and discharge rates for each size interval computed by the model.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Rates
Size Display Size of each interval in internal mesh series.
MeanSize Display Geometric mean size of each interval in internal mesh series.
R Display Value of breakage rate, , for each size interval, for each ore species.
D Display Value of discharge rate, , for each size interval.
Ecs Display Value of the specific comminution energy for each size interval.

Load page

This page displays information about the balls, solids and liquids that currently comprise the mill load.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Distribution
Name Display Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream.
IntervalCount Display Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream.
SpWithPSDCount Display Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality.
Load
SolidMass / SMt Display The mass of solids with the SysCAD size distribution property currently in the mill.
LiquidMass / LMt Display The mass of liquids currently in the mill.
BallMass / BMt Display The mass of ball media in the mill.
Size Display Size of each interval in the external mesh series.
MeanSize Display Geometric mean size of each interval in the external mesh series.
Load Display The mass of solids with the SysCAD size distribution property currently in the mill, by size and species.}}

Power page

This optional page displays the inputs and results for alternative mill power models. The page is only visible if PowerModels is selected on the MD_Mill page.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Power
HoggFuerstenau CheckBox Shows inputs and results for tumbling mill power calculations using the Hogg and Fuerstenau method.
MorrellC CheckBox Shows inputs and results for tumbling mill power calculations using the Morrell Continuum method.
MorrellE CheckBox Shows inputs and results for tumbling mill power calculations using the Morrell Empirical method.
MorrellD CheckBox Shows inputs and results for tumbling mill power calculations using the Morrell Discrete Shell method.
HildenPowell CheckBox Shows inputs and results for tumbling mill power calculations using the Hilden and Powell method.

MediaStrings page

This page displays the inputs and results for grinding mill media string calculations. The page is only visible if MediaStrings is selected on the MD_Mill page.

MediaTraj page

This page displays the inputs and results for tumbling mill media trajectory calculations. The page is only visible if MediaTrajectory is selected on the MD_Mill page.

About page

This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
About
HelpLink ButtonLicensingHelp.png Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required.
Information ButtonCopyToClipboard.png Copies Product and License information to the Windows clipboard.
Product
Name Display Met Dynamics software product name
Version Display Met Dynamics software product version number.
BuildDate Display Build date and time of the Met Dynamics Models SysCAD Add-On.
License
File ButtonBrowse.png This is used to locate a Met Dynamics software license file.
Location Display Type of Met Dynamics software license or file name and path of license file.
SiteCode Display Unique machine identifier for license authorisation.
ReqdAuth Display Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime.
Status Display License status, LICENSE_OK indicates a valid license, other messages report licensing errors.
IssuedTo Display Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to.
ExpiryDate Display Only visible if Met Dynamics license file is used. License expiry date.
DaysLeft Display Only visible if Met Dynamics license file is used. Days left before the license expires.

See also

External links

References

  1. ↑ Napier-Munn, T.J., Morrell, S., Morrison, R.D. and Kojovic, T., 1996. Mineral comminution circuits: their operation and optimisation. Julius Kruttschnitt Mineral Research Centre, Indooroopilly, QLD.
  2. ↑ Leung, K., Morrison, R.D. and Whiten, W.J., 1987. An Energy Based Ore Specific Model for Autogenous and Semi-autogenous Grinding, Copper 87, Vina del Mar, Vol. 2, pp 71 - 86
  3. ↑ Morrell, S. and Morrison, R.D., 1996. AG and SAG mill circuit selection and design by simulation. In International Conference on Autogenous and Semiautogenous Grinding Technology (Vol. 2, pp. 769-790).
  4. ↑ Morrell, S., Valery, W., Banini, G. and Latchireddi, S., 2001. Developments in AG/SAG mill modelling. Proceedings of Autogenous and Semiautogenous Grinding Technology, Vancouver, pp.71-84.
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=AG/SAG_Mill_(Variable_Rates)&oldid=3181"