Description
This article describes the Altun and Benzer (2014) model for high efficiency air classifiers.[1]
High efficiency air classifiers may be alternatively described as dynamic or third generation air classifiers.
Model theory
The Altun air classifier model applies the Whiten-Beta efficiency curve to partition particles to the overflow stream:
![{\displaystyle E_{\rm {oa}}({\bar {d}}_{i})=C\left[{\dfrac {\left(1+\beta \beta ^{*}{\dfrac {{\bar {d}}_{i}}{d_{\rm {50c}}}}\right)(\exp(\alpha )-1)}{\exp \left(\alpha \beta ^{*}{\dfrac {{\bar {d}}_{i}}{d_{\rm {50c}}}}\right)+\exp(\alpha )-2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/692eadc8e565caa11dfb67b8220c1b59aeb45652)
where:
 is the index of the size interval,
is the index of the size interval,  ,
,  is the number of size intervals
is the number of size intervals is the fraction of particles of size interval
is the fraction of particles of size interval  in the feed reporting to the overflow stream (frac)
in the feed reporting to the overflow stream (frac) is the geometric mean size of particles in size interval
is the geometric mean size of particles in size interval  (mm)
(mm) is the corrected size at which 50% of the particle mass reports to underflow and 50% to overflow (mm)
is the corrected size at which 50% of the particle mass reports to underflow and 50% to overflow (mm) is the fraction of feed liquids (or fines) split to overflow (frac)
is the fraction of feed liquids (or fines) split to overflow (frac) is a parameter representing the sharpness of separation
is a parameter representing the sharpness of separation is a term introduced to accommodate the so-called fish-hook effect, and controls the initial rise in the efficiency curve at finer sizes
is a term introduced to accommodate the so-called fish-hook effect, and controls the initial rise in the efficiency curve at finer sizes is computed to ensure the Whiten-Beta function preserves the definition of
is computed to ensure the Whiten-Beta function preserves the definition of  in the presence of the fish-hook, i.e.
in the presence of the fish-hook, i.e.  at
at 
Additional relations link terms of the efficiency curve equation with operating parameters.
Corrected cut size
The corrected cut size,  (mm), is:
(mm), is:

where:
 is the classifier air flow rate (m3/h)
is the classifier air flow rate (m3/h) is the rotor speed of the classifier (m/s)
is the rotor speed of the classifier (m/s) is the flow rate of -36+3 µm size particles in the feed (t/h)
is the flow rate of -36+3 µm size particles in the feed (t/h) and
and  are the coefficient and exponent, respectively, of the cut size equation.
are the coefficient and exponent, respectively, of the cut size equation.
Sharpness of separation
The sharpness of separation term,  , is estimated by:
, is estimated by:

where:
 is the classifier chamber diameter (m)
is the classifier chamber diameter (m) is the dust loading of the classifier feed (kg/m3)
is the dust loading of the classifier feed (kg/m3) and
and  are the coefficient and exponent, respectively, of the sharpness of separation equation.
are the coefficient and exponent, respectively, of the sharpness of separation equation.
The dust loading,  (kg/m3), is calculated from the feed and air flow rates:
(kg/m3), is calculated from the feed and air flow rates:

where  is the mass flow rate of solids in the feed (t/h)
is the mass flow rate of solids in the feed (t/h)
Fines bypass
The fraction of the finest particles reporting to overflow,  (frac), is:
(frac), is:

where  and
and  are the coefficient and exponent, respectively, of the fines bypass equation.
are the coefficient and exponent, respectively, of the fines bypass equation.
Fish-hook parameter
The parameter controlling the initial rise of the efficiency curve in fines sizes (fish-hook),  , is:
, is:

where  ,
,  and
and  are the coefficient, exponent and constant, respectively, of the fish-hook equation.
are the coefficient, exponent and constant, respectively, of the fish-hook equation.
Altun and Benzer (2014) also provide an equation for the  term of the efficiency equation. However, Whiten's definition of
term of the efficiency equation. However, Whiten's definition of  requires its value to be computed in complement to the specified value of
requires its value to be computed in complement to the specified value of  in the efficiency equation (see Partition (Size, Whiten-Beta) for more information).
in the efficiency equation (see Partition (Size, Whiten-Beta) for more information).
Therefore, the  equation is excluded from this implementation of Altun and Benzer's (2014) air classifier model.
equation is excluded from this implementation of Altun and Benzer's (2014) air classifier model.
Equation parameters
Altun and Benzer's (2014) test work was conducted on a range of Sepol, Sepax and Sepmaster industrial scale dynamic air classifiers. The parameter values in Table 1 were derived by regression analyses of their industrial sampling results.
Table 1. Air classifier model equation parameters (after Altun and Benzer, 2014).[1]
| Equation |
Coefficient,  |
Exponent,  |
Constant, 
|
 |
0.905 |
1.2679 |
-
|
 |
0.4048 |
0.7775 |
-
|
 |
10.467 |
1.4171 |
-
|
 |
0.4417 |
1.4171 |
0.1293
|
This implementation of the air classifier model allows a user to specify the values of the equation coefficients, exponents and constants directly. Altun and Benzer's (2014) values may be used, or new values derived from specific industrial or laboratory test work programmes.
Additional notes
Altun and co-workers have published subsequent journal articles outlining similar model treatments for multi-component feeds, where particle density differences and agglomeration are observed to affect classification performance.[2][3]
However, this work was only conducted on laboratory scale equipment (Alpine 100 MZR) rather than operating industrial air classifiers. Additional non-standard material measurements are also required (e.g. fluidity index). As such, these model implementations are not included here.
Excel
The Altun air classifier model may be invoked from the Excel formula bar with the following function call:
=mdUnit_AirClassifier_Altun(Parameters as Range, Size as Range, Feed as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row ( ) x column (
) x column ( ) format:
) format:

where:
 is the number of size intervals
is the number of size intervals is the number of ore types
is the number of ore types is the size of the square mesh interval that mass is retained on (mm)
is the size of the square mesh interval that mass is retained on (mm) , i.e. descending size order from top size (
, i.e. descending size order from top size ( ) to sub mesh (
) to sub mesh ( mm)
mm) is the mass flow rate of liquids in the feed (t/h)
is the mass flow rate of liquids in the feed (t/h)
Results
The results are displayed in Excel as an array corresponding to the matrix notation below:

where:
 is the mass flow rate of liquids to the overflow stream (t/h)
is the mass flow rate of liquids to the overflow stream (t/h) is the mass flow rate of liquids to the underflow stream (t/h)
is the mass flow rate of liquids to the underflow stream (t/h)
Example
The images below show the selection of input arrays and output results in the Excel interface.
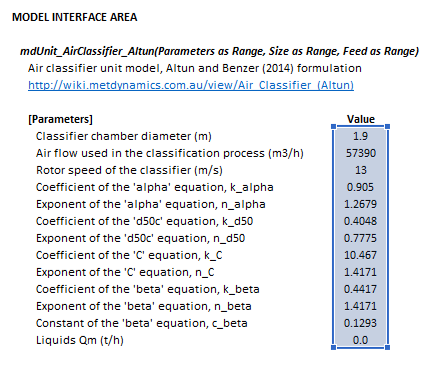 Figure 1. Example showing the selection of the Parameters (blue frame) array in Excel. |
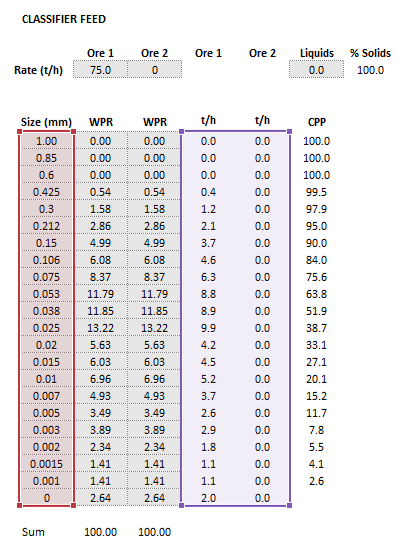 Figure 2. Example showing the selection of the Size (red frame), OreSG (green frame) and Feed (purple frame) arrays in Excel. |
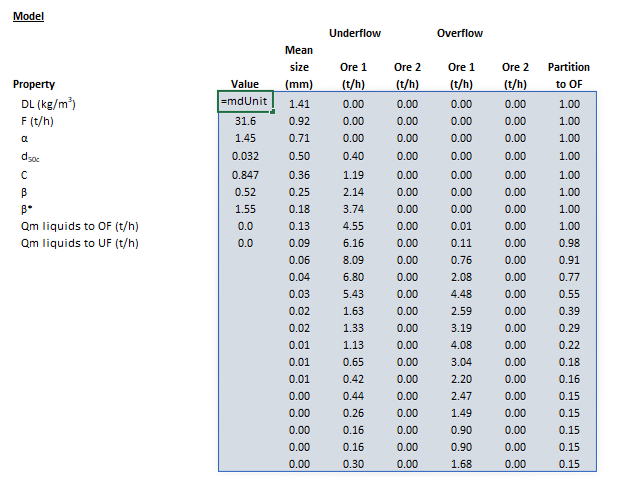 Figure 3. Example showing the selection of the Results (light blue frame) array in Excel. |
SysCAD
 This section is currently under construction. Please check back later for updates and revisions. This section is currently under construction. Please check back later for updates and revisions.
|
See also
References
- ↑ 1.0 1.1 Altun, O. and Benzer, H., 2014. Selection and mathematical modelling of high efficiency air classifiers. Powder Technology, 264, pp.1-8.
- ↑ Altun, O., Toprak, A., Benzer, H. and Darilmaz, O., 2016. Multi component modelling of an air classifier. Minerals Engineering, 93, pp.50-56.
- ↑ Altun, O., 2022. Air classification performances of the components within the varied feed blends. Powder Technology, 399, p.117092.
![{\displaystyle E_{\rm {oa}}({\bar {d}}_{i})=C\left[{\dfrac {\left(1+\beta \beta ^{*}{\dfrac {{\bar {d}}_{i}}{d_{\rm {50c}}}}\right)(\exp(\alpha )-1)}{\exp \left(\alpha \beta ^{*}{\dfrac {{\bar {d}}_{i}}{d_{\rm {50c}}}}\right)+\exp(\alpha )-2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/692eadc8e565caa11dfb67b8220c1b59aeb45652)
















































