Mass Balancing (n-Product Formula)

Description

This article describes a methodology for estimating the solids mass split and recovery of multiple assayed components from a process step with any number of product streams.

Model theory

The method of mass flow errors is applied to estimate the solids split and recovery of multiple assayed components to an arbitrary number of product streams.

The assays used must show a reasonable degree of degree of separation across the process for the n-product formula to return sensible results.

Mineral compositions, particle size distributions and water fractions can be substituted in place of metal assays in the method.

Unweighted estimates

The solids mass flow split to each product stream is found by minimising the unweighted sum of squares of the differences between the mass flows of each assayed component in the feed and product streams, i.e.

$\mathrm {argmin} \left\{\sum \limits _{i=1}^{m}{\Delta _{i}}^{2}\right\}$

where:

$\Delta _{i}={f_{i}-\sum \limits _{j=1}^{n}{\beta _{j}p_{ij}}}\quad :\quad 0\leq \beta _{j}\leq 1,\quad \sum \beta _{j}=1,\quad m\geq n-1$

and:

• $m$ is the number of component assays
• $n$ is the number of product streams
• $f_{i}$ is the assay of component $i$ in the feed stream
• $p_{ij}$ is the assay of component $i$ in product stream $j$
• $\beta _{j}$ is solids mass split to product stream $j$ (frac)

The feed stream assays may be reconstituted by summing the product stream assays at the estimated solids mass splits:

${\hat {f}}_{i}=\sum \limits _{j=1}^{n}\beta _{j}p_{ij}$

where ${\hat {f}}_{i}$ is the reconstituted assay of component $i$ in the feed stream.

The recovery of each assayed component $i$ to each product stream $j$, $R_{ij}$ (frac), is then:

$R_{ij}={\dfrac {\beta _{j}p_{ij}}{{\hat {f}}_{i}}}$

The assays of a single component which are larger than other components (even by choice of units) will tend to dominate the unweighted estimates, for obvious reasons.

Weighted estimates

A weighted sum of squares for minimisation can be generated which takes into account measurement uncertainty.

The propagation of variance approximation states that the variance of a function is the sum of the product of the variance of each input and the square of its partial derivative, and so:

${\sigma _{\Delta i}}^{2}={\sigma _{{\rm {f}}i}}^{2}+\sum \limits _{j=1}^{n}{\beta _{j}}^{2}{\sigma _{ij}}^{2}$

where:

• $\sigma _{{\rm {f}}i}$ is the standard deviation of the assay of component $i$ in the feed stream
• $\sigma _{ij}$ is the standard deviation of the assay of component $i$ in product stream $j$

The weighted solids splits is therefore found from:

$\mathrm {argmin} \left\{\sum \limits _{i=1}^{m}{\dfrac {{\Delta _{i}}^{2}}{{\sigma _{\Delta i}}^{2}}}\right\}$

and the reconstituted feed assays and component recoveries are computed as for the unweighted case.

Excel

The n-product formula may be invoked from the Excel formula bar with the following function call:

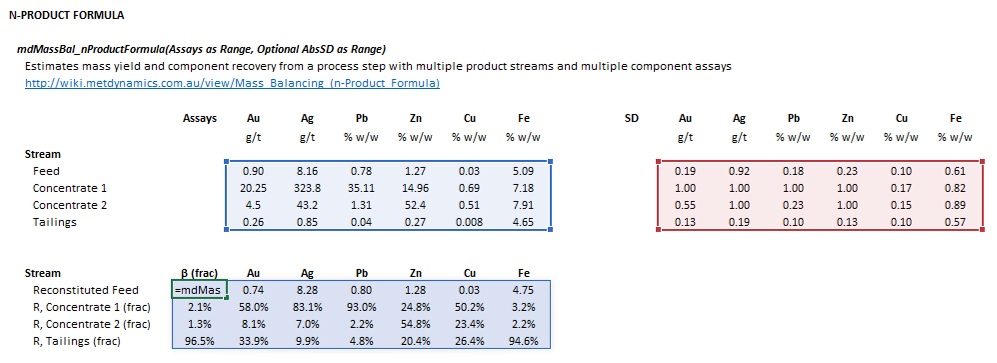
=mdMassBal_nProductFormula(Assays as Range, Optional AbsSD as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:

${\begin{aligned}{\mathit {Assay}}&={\begin{bmatrix}f_{1}&\cdots &f_{m}\\p_{11}&\cdots &p_{m1}\\\vdots &\ddots &\vdots \\p_{1n}&\cdots &p_{mn}\\\end{bmatrix}}\\\\{\mathit {AbsSD}}&={\begin{bmatrix}\sigma _{\rm {f1}}&\cdots &\sigma _{{\rm {f}}m}\\\sigma _{11}&\cdots &\sigma _{m1}\\\vdots &\ddots &\vdots \\\sigma _{1n}&\cdots &\sigma _{mn}\\\end{bmatrix}}\\\end{aligned}}$ ${\begin{aligned}{\mathit {mdMassBal\_nProductFormula}}&={\begin{bmatrix}\beta _{\rm {f}}{\text{ (frac)}}&{\hat {f}}_{1}{\text{ (frac)}}&\cdots &{\hat {f}}_{m}{\text{ (frac)}}\\\beta _{1}{\text{ (frac)}}&R_{11}{\text{ (frac)}}&\cdots &R_{m1}{\text{ (frac)}}\\\vdots &\vdots &\ddots &\vdots \\\beta _{n}{\text{ (frac)}}&R_{1n}{\text{ (frac)}}&\cdots &R_{mn}{\text{ (frac)}}\\\end{bmatrix}}\end{aligned}}$ where: $\beta _{\rm {f}}$ is total mass fraction of solids in the feed (frac), i.e. $\beta _{\rm {f}}=\sum \nolimits _{i}^{n}{\beta _{i}}=1$ the unweighted sum of squares approach is used if $AbsSD$ is omitted.

Figure 1. Example showing the selection of the Assay (blue frame), AbsSD (red frame), and Results (light blue frame) arrays in Excel.

See also

• Mass Balancing (Two-Product Formula)
• Mass Balancing (Three-Product Formula)