Mass Balancing (n-Product Formula): Difference between revisions
imported>Scott.Munro m (→Excel) |
imported>Scott.Munro m (→Transposed) |
||
| Line 37: | Line 37: | ||
:<math>R_{ij} = \dfrac{\beta_j p_{ij}}{\hat{f}_i}</math> | :<math>R_{ij} = \dfrac{\beta_j p_{ij}}{\hat{f}_i}</math> | ||
=== Weighted estimates === | === Weighted estimates === | ||
| Line 49: | Line 47: | ||
where: | where: | ||
* <math>\sigma_{{\rm f}i}</math> is the standard deviation of the assay of component <math>i</math> in the feed stream | * <math>\sigma_{{\rm f}i}</math> is the absolute standard deviation of the assay of component <math>i</math> in the feed stream | ||
* <math>\sigma_{ij}</math> is the standard deviation of the assay of component <math>i</math> in product stream <math>j</math> | * <math>\sigma_{ij}</math> is the absolute standard deviation of the assay of component <math>i</math> in product stream <math>j</math> | ||
The weighted solids splits is therefore found from: | The weighted solids splits is therefore found from: | ||
| Line 73: | Line 71: | ||
# As number of randomised draws increases, the mean values and variances of the mass splits and recoveries will approach their true values. | # As number of randomised draws increases, the mean values and variances of the mass splits and recoveries will approach their true values. | ||
--> | --> | ||
=== Additional notes === | |||
==== Absolute and relative standard deviations ==== | |||
The assay standard deviations required for the weighted estimates, (<math>\sigma_{\rm f},\sigma_{ij}</math>), are ''absolute'' standard deviations, and posses the same units as the assay measurement. | |||
However, many other literature sources quote ''relative'' standard deviations, usually as percentages, which must be converted to absolute values. For example: | |||
:<math>\sigma_{\rm fi} = \mathrm{RSD}_{\rm fi} . f_i </math> | |||
for the feed stream assays, where <math>\mathrm{RSD}</math> is the Relative Standard Deviation (frac). | |||
Care must be taken to differentiate between absolute and relative values when applying error models, e.g. the Whiten approach for particle size distributions.{{Greet (2010)}}{{Napier-Munn et al. (1996)}} | |||
==== Component assay magnitude ==== | |||
Component assays with larger values will tend to dominate the results of the method of mass flow errors. For example, component assays with values of thousands of parts per million will affect the solids mass split more than components with value of a fraction of a weight percent. | |||
This can be addressed as follows: | |||
* For the unweighted estimates case, the measured assay values can be scaled to more appropriate units, e.g. 100g/t rather than g/t. | |||
* For the weighted estimates case, the absolute standard deviations can be scaled to produce the same effect. | |||
The scaling factors applied in either case are arbitrary, and should be selected to reflect the relative "importance" or "confidence" of the component measurement. | |||
== Excel == | == Excel == | ||
| Line 78: | Line 101: | ||
The n-product formula may be invoked from the Excel formula bar with the following function call: | The n-product formula may be invoked from the Excel formula bar with the following function call: | ||
<syntaxhighlight lang="vb">=mdMassBal_nProductFormula(Assays as Range, Optional AbsSD as Range)</syntaxhighlight> | <syntaxhighlight lang="vb">=mdMassBal_nProductFormula(Assays as Range, Optional AbsSD as Range, Optional Transposed as Boolean = False)</syntaxhighlight> | ||
{{Excel (Text, Help, No Arguments)}} | {{Excel (Text, Help, No Arguments)}} | ||
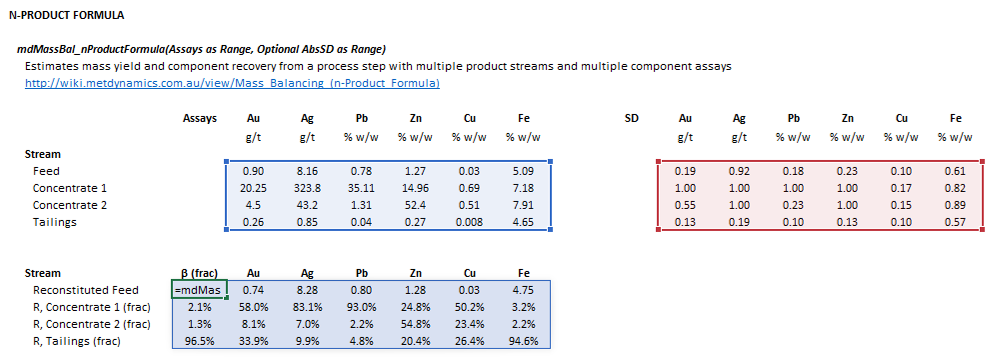
The input parameters and calculation results are defined below in matrix notation, along with | The input parameters and calculation results are defined below in matrix notation, along with example images showing the selection of the same cells and arrays in the Excel interface. | ||
=== Default === | |||
The following default arrangement of inputs and results ranges apply when the formula argument ''Transposed'' is '''false''' or omitted: | |||
{| | {| | ||
| Line 128: | Line 155: | ||
| | | | ||
::[[File:NProductFormula3.png|frame|Figure 1. Example showing the selection of the '''Assay''' (blue frame), '''AbsSD''' (red frame), and '''Results''' (light blue frame) arrays in Excel.]] | ::[[File:NProductFormula3.png|frame|Figure 1. Example showing the selection of the '''Assay''' (blue frame), '''AbsSD''' (red frame), and '''Results''' (light blue frame) arrays in Excel.]] | ||
|} | |||
=== Transposed === | |||
The following arrangement of inputs and results ranges apply when the formula argument ''Transposed'' is '''true''': | |||
{| | |||
|- style="vertical-align:top;" | |||
| | |||
{| | |||
|- style="vertical-align:top;" | |||
| | |||
:<math> | |||
\begin{align} | |||
\mathit{Assay} & = | |||
\begin{bmatrix} | |||
f_1 & p_{11} & \cdots & p_{1n}\\ | |||
\vdots & \vdots & \ddots\\ | |||
f_m & p_{1m} & \cdots & p_{mn}\\ | |||
\end{bmatrix}\\ | |||
\\ | |||
\mathit{AbsSD} & = | |||
\begin{bmatrix} | |||
\sigma_{{\rm f} 1} & \sigma_{11} & \cdots & \sigma_{1n}\\ | |||
\vdots & \vdots & \ddots\\ | |||
\sigma_{{\rm f} m} & \sigma_{1m} & \cdots & \sigma_{mn}\\ | |||
\end{bmatrix}\\ | |||
\end{align}</math> | |||
| | |||
::<math> | |||
\begin{align} | |||
\mathit{mdMassBal\_nProductFormula} & = | |||
\begin{bmatrix} | |||
\beta_{\rm f}\text{ (frac)} & \beta_1\text{ (frac)} & \cdots & \beta_n\text{ (frac)}\\ | |||
\hat{f}_1\text{ (frac)} & R_{11}\text{ (frac)} & \cdots & R_{1n}\text{ (frac)}\\ | |||
\vdots & \vdots & \ddots & \vdots\\ | |||
\hat{f}_m\text{ (frac)} & R_{m1}\text{ (frac)} & \cdots & R_{mn}\text{ (frac)}\\ | |||
\end{bmatrix} | |||
\end{align} | |||
</math> | |||
|- style="vertical-align:top;" | |||
|colspan="2"| | |||
|} | |||
| | |||
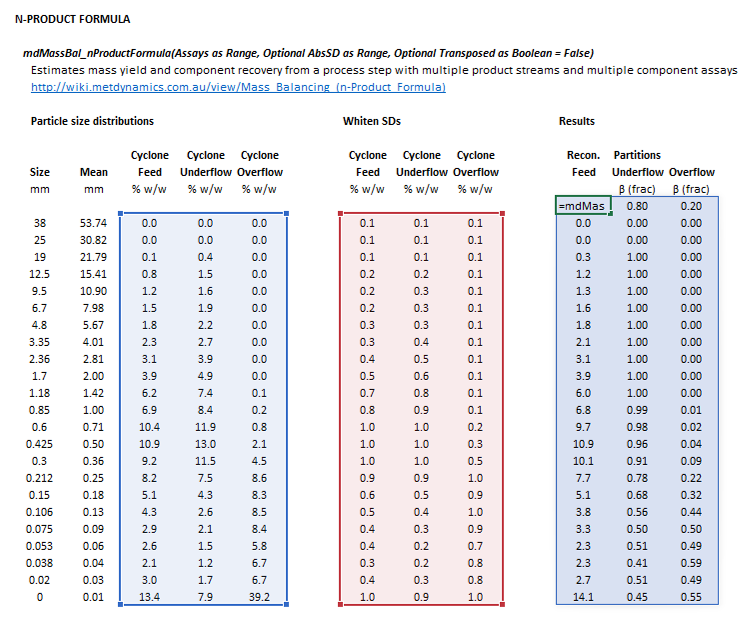
::[[File:NProductFormula4.png|frame|Figure 2. Example showing the selection of the '''Assay''' (blue frame), '''AbsSD''' (red frame), and '''Results''' (light blue frame) arrays in Excel when <math>\mathit{Transposed} = \mathrm{True}</math>.]] | |||
|} | |} | ||
Revision as of 06:14, 31 July 2024
Description
This article describes a methodology for estimating the solids mass split and recovery of multiple assayed components from a process step with any number of product streams.
Model theory
The method of mass flow errors is applied to estimate the solids split and recovery of multiple assayed components to an arbitrary number of product streams.[1]
The assays used must show a reasonable degree of degree of separation across the process for the n-product formula to return sensible results.
Mineral compositions, particle size distributions and water fractions can be substituted in place of metal assays in the method.
Unweighted estimates
The solids mass flow split to each product stream is found by minimising the unweighted sum of squares of the differences between the mass flows of each assayed component in the feed and product streams, i.e.
- [math]\displaystyle{ \mathrm{argmin} \left \{ \sum\limits_{i=1}^m {\Delta_i}^2 \right \} }[/math]
where:
- [math]\displaystyle{ \Delta_i = {f_i - \sum\limits_{j=1}^n {\beta_j p_{ij}}} \quad : \quad 0 \leq \beta_j \leq 1, \quad \sum \beta_j = 1, \quad m \geq n-1 }[/math]
and:
- [math]\displaystyle{ m }[/math] is the number of component assays
- [math]\displaystyle{ n }[/math] is the number of product streams
- [math]\displaystyle{ f_i }[/math] is the assay of component [math]\displaystyle{ i }[/math] in the feed stream
- [math]\displaystyle{ p_{ij} }[/math] is the assay of component [math]\displaystyle{ i }[/math] in product stream [math]\displaystyle{ j }[/math]
- [math]\displaystyle{ \beta_j }[/math] is solids mass split to product stream [math]\displaystyle{ j }[/math] (frac)
The feed stream assays may be reconstituted by summing the product stream assays at the estimated solids mass splits:
- [math]\displaystyle{ \hat{f}_i = \sum\limits_{j=1}^n \beta_j p_{ij} }[/math]
where [math]\displaystyle{ \hat{f}_i }[/math] is the reconstituted assay of component [math]\displaystyle{ i }[/math] in the feed stream.
The recovery of each assayed component [math]\displaystyle{ i }[/math] to each product stream [math]\displaystyle{ j }[/math], [math]\displaystyle{ R_{ij} }[/math] (frac), is then:
- [math]\displaystyle{ R_{ij} = \dfrac{\beta_j p_{ij}}{\hat{f}_i} }[/math]
Weighted estimates
A weighted sum of squares for minimisation can be generated which takes into account measurement uncertainty.
The propagation of variance approximation states that the variance of a function is the sum of the product of the variance of each input and the square of its partial derivative, and so:[1]
- [math]\displaystyle{ {\sigma_{\Delta i}}^2 = {\sigma_{{\rm f}i}}^2 + \sum\limits_{j=1}^n {\beta_j}^2 {\sigma_{ij}}^2 }[/math]
where:
- [math]\displaystyle{ \sigma_{{\rm f}i} }[/math] is the absolute standard deviation of the assay of component [math]\displaystyle{ i }[/math] in the feed stream
- [math]\displaystyle{ \sigma_{ij} }[/math] is the absolute standard deviation of the assay of component [math]\displaystyle{ i }[/math] in product stream [math]\displaystyle{ j }[/math]
The weighted solids splits is therefore found from:
- [math]\displaystyle{ \mathrm{argmin} \left \{ \sum\limits_{i=1}^m \dfrac{{\Delta_i}^2}{{\sigma_{\Delta i}}^2} \right \} }[/math]
and the reconstituted feed assays and component recoveries are computed as for the unweighted case.
Additional notes
Absolute and relative standard deviations
The assay standard deviations required for the weighted estimates, ([math]\displaystyle{ \sigma_{\rm f},\sigma_{ij} }[/math]), are absolute standard deviations, and posses the same units as the assay measurement.
However, many other literature sources quote relative standard deviations, usually as percentages, which must be converted to absolute values. For example:
- [math]\displaystyle{ \sigma_{\rm fi} = \mathrm{RSD}_{\rm fi} . f_i }[/math]
for the feed stream assays, where [math]\displaystyle{ \mathrm{RSD} }[/math] is the Relative Standard Deviation (frac).
Care must be taken to differentiate between absolute and relative values when applying error models, e.g. the Whiten approach for particle size distributions.[1][2]
Component assay magnitude
Component assays with larger values will tend to dominate the results of the method of mass flow errors. For example, component assays with values of thousands of parts per million will affect the solids mass split more than components with value of a fraction of a weight percent.
This can be addressed as follows:
- For the unweighted estimates case, the measured assay values can be scaled to more appropriate units, e.g. 100g/t rather than g/t.
- For the weighted estimates case, the absolute standard deviations can be scaled to produce the same effect.
The scaling factors applied in either case are arbitrary, and should be selected to reflect the relative "importance" or "confidence" of the component measurement.
Excel
The n-product formula may be invoked from the Excel formula bar with the following function call:
=mdMassBal_nProductFormula(Assays as Range, Optional AbsSD as Range, Optional Transposed as Boolean = False)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with example images showing the selection of the same cells and arrays in the Excel interface.
Default
The following default arrangement of inputs and results ranges apply when the formula argument Transposed is false or omitted:
|
| ||||
Transposed
The following arrangement of inputs and results ranges apply when the formula argument Transposed is true:
|
| ||||
See also
References
- ↑ 1.0 1.1 1.2 Greet, C.J. ed., 2010. Flotation plant optimisation: a metallurgical guide to identifying and solving problems in flotation plants. Australasian Institute of Mining and Metallurgy.
- ↑ Napier-Munn, T.J., Morrell, S., Morrison, R.D. and Kojovic, T., 1996. Mineral comminution circuits: their operation and optimisation. Julius Kruttschnitt Mineral Research Centre, Indooroopilly, QLD.