Ball Mill (Overfilling): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
m (1 revision imported)
imported>Scott.Munro
 
(3 intermediate revisions by the same user not shown)
Line 1: Line 1:
== Description ==
== Description ==


This article describes several methods for estimating the maximum volumetric flow capacity of an '''''overflow ball mill''''', including the '''Shi''' (2016) and '''Arbiter''' (1990) approaches.{{Shi (2016)}}{{Arbiter (1990)}}
This article describes several methods for estimating the maximum volumetric flow capacity of an '''''overflow ball mill''''', including the '''Shi''' (2016) and '''Arbiter''' (1991) approaches.{{Shi (2016)}}{{Arbiter (1991)}}


== Model theory ==
== Model theory ==


{{Restricted content}}
<hide>
</hide><div class="user-show">
=== Shi method ===
=== Shi method ===
</div><hide>


[[File:BallMillOverfilling1.png|thumb|450px|Figure 1. Overflow discharge tumbling mill profile showing Shi's assumed charge and slurry pool areas.]]
[[File:BallMillOverfilling1.png|thumb|450px|Figure 1. Overflow discharge tumbling mill profile showing Shi's assumed charge and slurry pool areas.]]


Shi estimated the residence time of an overflow ball mill by considering the volume of slurry present in the grinding media interstices and slurry pool.
Shi (2016) estimated the residence time of an overflow ball mill by considering the volume of slurry present in the grinding media interstices and slurry pool.


This was accomplished by adopting Morrell's (1996) simplified charge geometry and calculating the volume of slurry resident in each of the areas A-C in Figure 1:{{Morrell (1996a)}}
This was accomplished by adopting Morrell's (1996) simplified charge geometry and calculating the volume of slurry resident in each of the areas A-C in Figure 1:{{Morrell (1996a)}}
Line 21: Line 26:
Estimating the slurry volume in areas A-C requires definition of the simplified charge geometry and slurry pool level for the mill in question.
Estimating the slurry volume in areas A-C requires definition of the simplified charge geometry and slurry pool level for the mill in question.


</hide><div class="user-show">
==== Charge position ====
==== Charge position ====
</div><hide>


The simplified charge geometry is defined by three parameters:
The simplified charge geometry is defined by three parameters:
* the angular position of the ''toe'' of the charge, <math>\theta_{\rm t}</math> (rad)
* the angular position of the ''toe'' of the charge, <math>\theta_{\rm t}</math> (rad),
* the angular position of the ''shoulder'' charge, <math>\theta_{\rm s}</math> (rad)
* the angular position of the ''shoulder'' charge, <math>\theta_{\rm s}</math> (rad), and
* the radius of the ''inner charge surface'', <math>R_i</math> (m)
* the radius of the ''inner charge surface'', <math>R_i</math> (m).


Morrell's equations are used to define the charge position, i.e.{{Morrell (1996a)}}
Morrell's equations are used to define the charge position, i.e.{{Morrell (1996a)}}
Line 36: Line 43:
where:
where:
* <math>J_{t}</math> is the volumetric fraction of the mill occupied by balls and coarse rock (including void space and interstitial slurry) (v/v)
* <math>J_{t}</math> is the volumetric fraction of the mill occupied by balls and coarse rock (including void space and interstitial slurry) (v/v)
* <math>\phi</math> (frac) is the theoretical [[Tumbling Mill (Speed)|fraction critical speed]]
* <math>\phi</math> (frac) is the theoretical [[Tumbling Mill (Speed)|fraction critical speed]].


The fraction of critical speed at which centrifuging actually occurs, <math>\phi_{\rm c}</math> (frac), is:
The fraction of critical speed at which centrifuging actually occurs, <math>\phi_{\rm c}</math> (frac), is:
Line 55: Line 62:
:<math>R_i = r_{\rm m} \left ( 1 - \frac{2 \pi \beta J_{\rm t}}{2 \pi + \theta_{\rm s} - \theta_{\rm t}} \right )^{0.5}</math>
:<math>R_i = r_{\rm m} \left ( 1 - \frac{2 \pi \beta J_{\rm t}}{2 \pi + \theta_{\rm s} - \theta_{\rm t}} \right )^{0.5}</math>


where the fraction of total charge in the active region, <math>\beta</math> (frac), is:
where <math>r_{\rm m}</math> is the radius of the mill (m), and the fraction of total charge in the active region, <math>\beta</math> (frac), is:


:<math>\beta = \frac{t_{\rm c}}{t_{\rm f} + t_{\rm c}}</math>
:<math>\beta = \frac{t_{\rm c}}{t_{\rm f} + t_{\rm c}}</math>
Line 65: Line 72:
where the mean rotational rate, <math>\bar N</math> (rev/s), is:
where the mean rotational rate, <math>\bar N</math> (rev/s), is:


:<math>\bar N \approx \frac{N_{\rm m}}{2}</math>
:<math>\bar N \approx \frac{N_{\rm m}}{2}</math>  
 
and <math>N_{\rm m}</math> is the rotational rate of the mill shell (rev/s).


The time taken to travel between the shoulder and toe of the charge in free flight during one revolution, <math>t_{\rm f}</math> (s), is:
The time taken to travel between the shoulder and toe of the charge in free flight during one revolution, <math>t_{\rm f}</math> (s), is:
Line 72: Line 81:


where the mean radial position <math>\bar r</math> (m), is:
where the mean radial position <math>\bar r</math> (m), is:
:<math>\bar r = \frac{r_{\rm m}}{2} \left [ 1 + \left ( 1 - \frac{2 \pi J_{\rm t}}{2 \pi + \theta_{\rm s} - \theta_{\rm t}} \right )^{0.5} \right ]</math>
:<math>\bar r = \frac{r_{\rm m}}{2} \left [ 1 + \left ( 1 - \frac{2 \pi J_{\rm t}}{2 \pi + \theta_{\rm s} - \theta_{\rm t}} \right )^{0.5} \right ]</math>


</hide><div class="user-show">
==== Slurry hold-up below pool level ====
==== Slurry hold-up below pool level ====
</div><hide>


The volume of slurry held up below the pool level in areas B and C, <math>V_1</math> (m<sup>3</sup>), is:
The volume of slurry held up below the pool level in areas B and C, <math>V_1</math> (m<sup>3</sup>), is:
Line 91: Line 103:
where <math>V_{\rm m}</math> is the volume of the mill (m<sup>3</sup>) and <math>R_{\rm m}</math> is the radius of the mill (m).
where <math>V_{\rm m}</math> is the volume of the mill (m<sup>3</sup>) and <math>R_{\rm m}</math> is the radius of the mill (m).


The volume of the mill is calculated as the sum of a cylinder and two right circular frustums:{{Gupta and Yan (2016)}}
The volume of the mill is calculated as the sum of a cylinder and two right circular frustums:{{Gupta and Yan (2016)}}


:<math>V_{\rm m} = \pi {R_{\rm m}}^2L + 2 \cdot \bigg[ \dfrac{\pi}{3} (R_{\rm m} - R_{\rm t}) \cdot \tan \alpha_{\rm c} \cdot \left ( {R_{\rm m}}^{2} + R_{\rm m} R_{\rm t} + {R_{\rm t}}^{2} \right) \bigg]</math>
:<math>V_{\rm m} = \pi {R_{\rm m}}^2L + 2 \cdot \bigg[ \dfrac{\pi}{3} (R_{\rm m} - R_{\rm t}) \cdot \tan \alpha_{\rm c} \cdot \left ( {R_{\rm m}}^{2} + R_{\rm m} R_{\rm t} + {R_{\rm t}}^{2} \right) \bigg]</math>


wher:
where:
* <math>L</math> is the length of the cylindrical (belly) section of the mill (m)
* <math>L</math> is the length of the cylindrical (belly) section of the mill (m)
* <math>R_{\rm t}</math> is the radius of the discharge trunnion (m)
* <math>R_{\rm t}</math> is the radius of the discharge trunnion (m)
Line 129: Line 141:
:<math>\varepsilon_{\rm d} = 0.4 + 0.228 \left [ 1 - \exp \left (-0.315\dfrac{\phi}{J_{\rm t}} \right) \right ]</math>
:<math>\varepsilon_{\rm d} = 0.4 + 0.228 \left [ 1 - \exp \left (-0.315\dfrac{\phi}{J_{\rm t}} \right) \right ]</math>


</hide><div class="user-show">
==== Slurry hold up above pool level ====
==== Slurry hold up above pool level ====
</div><hide>


The volume of slurry held up in the grinding media interstices above the slurry pool level in area A, <math>V_2</math> (m<sup>3</sup>), is:
The volume of slurry held up in the grinding media interstices above the slurry pool level in area A, <math>V_2</math> (m<sup>3</sup>), is:
Line 139: Line 153:
:<math>S_{\rm ball\,above\,pool} = 0.5 (\theta_{\rm s} + \alpha)({R_{\rm m}}^2 - {R_{\rm t}}^2)</math>
:<math>S_{\rm ball\,above\,pool} = 0.5 (\theta_{\rm s} + \alpha)({R_{\rm m}}^2 - {R_{\rm t}}^2)</math>


</hide><div class="user-show">
==== Residence time and overfilling ====
==== Residence time and overfilling ====
</div><hide>


The total volume of slurry hold up in the mill is <math>V_{\rm total}=V_1+V_2</math> (m<sup>3</sup>).
The total volume of slurry hold up in the mill is <math>V_{\rm total}=V_1+V_2</math> (m<sup>3</sup>).
Line 165: Line 181:
The maximum volumetric flow rate of the mill, <math>Q_{\rm Max}</math> (m<sup>3</sup>/s), at the residence time limit <math>t_{\rm Limit}</math> may be back-calculated using the above relations. However, as the height of slurry above the trunnion lip (<math>h</math>), and hence residence time (<math>t_{\rm Res}</math>), is a function of flow rate, no analytical solution is available and a numerical method is required for computation.
The maximum volumetric flow rate of the mill, <math>Q_{\rm Max}</math> (m<sup>3</sup>/s), at the residence time limit <math>t_{\rm Limit}</math> may be back-calculated using the above relations. However, as the height of slurry above the trunnion lip (<math>h</math>), and hence residence time (<math>t_{\rm Res}</math>), is a function of flow rate, no analytical solution is available and a numerical method is required for computation.


</hide><div class="user-show">
=== Arbiter method ===
=== Arbiter method ===
</div><hide>


Arbiter describes two approaches for identifying the overfilling of an overflow discharge ball mill:
Based on an analysis of industrial ball mills at five operations, Arbiter (1991) postulated that the axial velocity of pulp through a mill should be less than 2.2% of the mill's tangential velocity. The ''Arbiter Flow Number'', <math>N_{\rm q}</math>, is defined as the ratio of axial to tangential velocity and is determined from:
#. the '''critical flow number''' method
#. the '''axial flow velocity''' method
 
Arbiter's limits are rearranged to yield the following relations for the maximum volumetric discharge rate of slurry from a mill:
 
:<math>Q_{N_{\rm q}} = 0.0217 \dfrac{\pi^2}{4} {D_{\rm m}}^3 N_{\rm eq} (0.5 - 0.66 J_{\rm t}) \cdot 60</math>


:<math>Q_{v_{\rm ax}} = 0.0769 \dfrac{\pi}{4} {D_{\rm m}}^{2} (0.5 - 0.66 J_{\rm t}) \cdot 3600</math>
:<math>N_{\rm q} = \dfrac{\left (\dfrac{Q}{\frac{\pi {D_{\rm m}}^2}{4} (0.5 - 0.66 J_{\rm t})}\right )}{\pi N_{\rm m} D_{\rm m}}, \quad N_{\rm q} < 0.0217</math>


where:
where:
* <math>Q_{N_{\rm q}}</math> is the critical flow number volumetric slurry discharge rate limit (m<sup>3</sup>/h)
* <math>Q</math> is the volumetric discharge rate of pulp from the mill (m3/s)
* <math>Q_{v_{\rm ax}}</math> is the axial velocity volumetric slurry discharge rate limit (m/s)
* <math>D_{\rm m}</math> is the mill diameter (m)
* <math>D_{\rm m}</math> is mill diameter (m)
* <math>N_{\rm eq}</math> is mill rotational speed (rev/min)
* <math>J_{\rm t}</math> is the volumetric charge fraction in the mill (v/v)
* <math>J_{\rm t}</math> is the volumetric charge fraction in the mill (v/v)
* <math>N_{\rm m}</math> is mill rotational speed (rev/min)


Overfilling may be a risk if the actual volumetric flow rate from the mill approaches or exceeds either of <math>(Q_{\rm Max})_{N_{\rm q}}</math> or <math>(Q_{\rm Max})_{v_{\rm ax}}</math>.
The Arbiter Flow Number equation may be rearranged to yield the following relation for the maximum volumetric discharge rate of slurry from a mill prior to overloading, <math>Q_{N_{\rm q}}</math> (m<sup>3</sup>/h):
 
== Additional notes ==


Shi estimated the residence times for a database of 121 overflow ball mills. These residence times are presented as cumulative frequency distributions in Figure 2, allowing the performance a given mill to be ranked against the database.
:<math>Q_{N_{\rm q}} = 0.0217 \dfrac{\pi^2}{4} {D_{\rm m}}^3 N_{\rm m} (0.5 - 0.66 J_{\rm t}) \cdot 3600</math>
 
:{|
|-
|style="padding: 10px" | [[File:BallMillOverfilling2.png|thumb|none|650px|Figure 2. Cumulative frequency distribution of the volume-based residence time of 121 mills in Shi's database (after Shi, 2016).{{Shi (2016)}}]]
|}


Arbiter's relations were developed from a limited database of five mills, the largest of which was 5.3 m diameter x 6.4 m length.
Overfilling may be a risk if the actual volumetric flow rate to/from the mill approaches or exceeds <math>Q_{N_{\rm q}}</math>.
</hide>


== Excel ==
== Excel ==
Line 243: Line 248:
The Arbiter overflow discharge ball mill overfilling model may be invoked from the Excel formula bar with the following function call:
The Arbiter overflow discharge ball mill overfilling model may be invoked from the Excel formula bar with the following function call:


<syntaxhighlight lang="vb">=mdMillOverfilling_Arbiter(Parameters as Range)(Parameters as Range)</syntaxhighlight>
<syntaxhighlight lang="vb">=mdMillOverfilling_Arbiter(Parameters as Range)</syntaxhighlight>


{{Excel (Text, Help, No Arguments)}}
{{Excel (Text, Help, No Arguments)}}
Line 262: Line 267:
\begin{bmatrix}
\begin{bmatrix}
Q_{N_{\rm q}}\text{ (m}^{3}\text{/h)}\\
Q_{N_{\rm q}}\text{ (m}^{3}\text{/h)}\\
Q_{v_{\rm ax}}\text{ (m}^{3}\text{/h)}\\
\end{bmatrix}\;\;\;\;\;\;
\end{bmatrix}\;\;\;\;\;\;
</math>
</math>
Line 368: Line 372:
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Estimated volumetric flow rate of slurry (solids + liquids) at Arbiters critical flow number limit.
|Estimated volumetric flow rate of slurry (solids + liquids) at Arbiters critical flow number limit.
|-
|Feed.SLQv.VmaxLimit
|style="background: #eaecf0" | Display
|Estimated volumetric flow rate of slurry (solids + liquids) at Arbiters axial velocity limit.
|}
|}


Latest revision as of 06:44, 1 May 2025

Description

This article describes several methods for estimating the maximum volumetric flow capacity of an overflow ball mill, including the Shi (2016) and Arbiter (1991) approaches.[1][2]

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Shi method

Charge position

Slurry hold-up below pool level

Slurry hold up above pool level

Residence time and overfilling

Arbiter method

Excel

Shi method

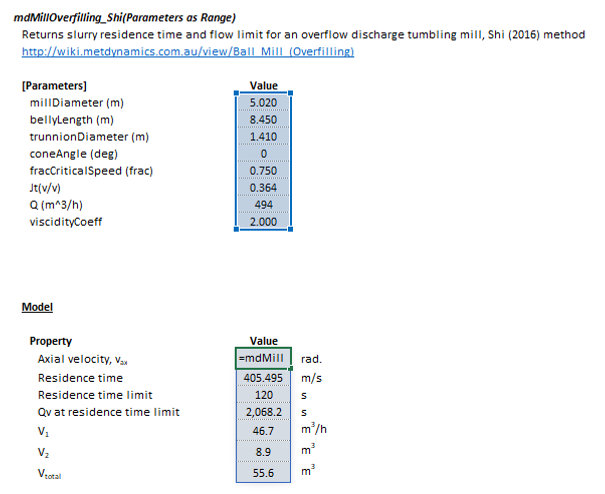
The Shi overflow discharge ball mill overfilling model may be invoked from the Excel formula bar with the following function call: 

=mdMillOverfilling_Shi(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

Figure 3. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

Arbiter method

The Arbiter overflow discharge ball mill overfilling model may be invoked from the Excel formula bar with the following function call: 

=mdMillOverfilling_Arbiter(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

Figure 4. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Ball Mill Overfilling Indicator model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Overfilling
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
Shi
MillDiameter Input/Display Diameter of the mill (inside liners).
BellyLength Input/Display Length of the cylindrical section (belly) of the mill (inside liners).
TrunnionDiameter Input/Display Diameter of the trunnion (inside liners).
ConeAngle Input/Display Angular displacement of the cone surface from the vertical direction.
FracCS Input/Display Fraction critical speed of the mill.
Jt Input/Display Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
ViscidityCoeff Input Coefficient of viscidity.
V1 Display Volume of slurry below slurry pool level.
V2 Display Volume of slurry above slurry pool level.
V1 Display Total volume of slurry in charge and pool.
AxialVelocity Display Axial velocity of slurry flow through the charge and pool.
tRes Display Residence time of slurry in mill.
tLimit Display Shi's suggested lower limit of residence time for mill. Based on mill diameter.
Feed.SLQv Display Volumetric flow rate of slurry (solids + liquids) in mill feed.
Feed.SLQv.Limit Display Estimated volumetric flow rate of slurry (solids + liquids) in mill feed at tLimit.
Overfilled True/False Indicates if tRes is less than tLimit, i.e. mill is overfilled.
Arbiter
MillDiameter Input/Display Diameter of the mill (inside liners).
FracCS Input/Display Fraction critical speed of the mill.
Jt Input/Display Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
Feed.SLQv Display Volumetric flow rate of slurry (solids + liquids) in mill feed.
Feed.SLQv.NqLimit Display Estimated volumetric flow rate of slurry (solids + liquids) at Arbiters critical flow number limit.

See also

References

  1. ↑ Shi, F., 2016. An overfilling indicator for wet overflow ball mills. Minerals Engineering, 95, pp.146-154.
  2. ↑ Arbiter, N., 1991. Dimensionality in ball mill dynamics. Mining, Metallurgy & Exploration, 8(2), pp.77-81.
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Ball_Mill_(Overfilling)&oldid=2553"