Hydrocyclone (Nageswararao): Difference between revisions
Scott Munro (talk | contribs) m (1 revision imported) |
imported>Scott.Munro mNo edit summary |
||
| (14 intermediate revisions by 3 users not shown) | |||
| Line 5: | Line 5: | ||
== Model theory == | == Model theory == | ||
{{Restricted content}} | |||
<hide> | |||
[[File:HydrocycloneNageswararao1.png|thumb|375px|Figure 1. The dimensions of a hydrocyclone required by the Nageswararao model.]] | [[File:HydrocycloneNageswararao1.png|thumb|375px|Figure 1. The dimensions of a hydrocyclone required by the Nageswararao model.]] | ||
</hide><div class="user-show"> | |||
=== Efficiency curve === | === Efficiency curve === | ||
</div><hide> | |||
The Nageswararao model applies the [[ | The Nageswararao model applies the [[Partition (Size, Whiten-Beta)|Whiten-Beta efficiency curve]] to partition particles to the overflow stream: | ||
{{Model theory (Text, Whiten-Beta Efficiency Curve)}} | {{Model theory (Text, Whiten-Beta Efficiency Curve)}} | ||
</hide><div class="user-show"> | |||
=== Corrected cut size === | === Corrected cut size === | ||
</div><hide> | |||
The corrected cut size, <math>d_{50c}</math> (m), is computed from: | The corrected cut size, <math>d_{\rm 50c}</math> (m), is computed from: | ||
:<math>d_{50c} = K_{D0} { | :<math>d_{\rm 50c} = K_{\rm D0} {D_{\rm c}}^{-0.65} \left ( \dfrac{D_{\rm o}}{D_{\rm c}} \right )^{0.52} \left ( \dfrac{D_{\rm u}}{D_{\rm c}} \right )^{-0.47} \left ( \dfrac{D_{\rm i}}{D_{\rm c}} \right )^{-0.5} \left ( \dfrac{L_{\rm c}}{D_{\rm c}} \right )^{0.2} \theta^{0.15} \left ( \dfrac{P}{\rho_{\rm p} g D_{\rm c}} \right )^{-0.22} \lambda^{0.93} (D_{\rm c})</math> | ||
where: | where: | ||
* <math>K_{D0}</math> is a calibration factor which should be fitted to operating data | * <math>K_{\rm D0}</math> is a calibration factor which should be fitted to operating data | ||
* <math> | * <math>D_{\rm c}</math> is diameter of the cyclone (m) | ||
* <math> | * <math>D_{\rm i}</math> is diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet (m) | ||
* <math> | * <math>D_{\rm o}</math> is diameter of the vortex finder (overflow) (m) | ||
* <math> | * <math>D_{\rm u}</math> is diameter of the apex/spigot (underflow) (m) | ||
* <math> | * <math>L_{\rm c}</math> is length of the cylindrical section (m) | ||
* <math>\theta</math> is the cone full angle (deg.) | * <math>\theta</math> is the cone full angle (deg.) | ||
* <math>P</math> is the pressure drop across the cyclone (kPa) | * <math>P</math> is the pressure drop across the cyclone (kPa) | ||
* <math>\ | * <math>\rho_{\rm p}</math> is the density of the feed slurry (t/m<sup>3</sup>) | ||
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>) | * <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>) | ||
The term <math>\lambda</math> is the hindered settling factor, and is defined as: | The term <math>\lambda</math> is the hindered settling factor, and is defined as: | ||
:<math>\lambda = \dfrac{10^{1. | :<math>\lambda = \dfrac{10^{1.82C_{\rm V}}}{8.05(1-C_{\rm V})^2}</math> | ||
where <math> | where <math>C_{\rm V}</math> is the volume fraction of solids in the feed (v/v). | ||
</hide><div class="user-show"> | |||
=== Liquids recovery === | === Liquids recovery === | ||
</div><hide> | |||
The fraction of feed liquid recovered to the underflow stream, <math> | The fraction of feed liquid recovered to the underflow stream, <math>R_{\rm f}</math>, is related to <math>C</math> (i.e. <math>C = 1 - R_{\rm f}</math>) and is computed as: | ||
:<math> | :<math>R_{\rm f} = K_{\rm W1} \left ( \dfrac{D_{\rm o}}{D_{\rm c}} \right )^{-1.19} \left ( \dfrac{D_{\rm u}}{D_{\rm c}} \right )^{2.4} \left ( \dfrac{D_{\rm i}}{D_{\rm c}} \right )^{-0.5} \left ( \dfrac{L_{\rm c}}{D_{\rm c}} \right )^{0.22} \theta^{-0.24} \left ( \dfrac{P}{\rho_{\rm p} g D_{\rm c}} \right )^{-0.53} \lambda^{0.27}</math> | ||
where <math>K_{W1}</math> is a calibration factor which should be fitted to operating data. | where <math>K_{\rm W1}</math> is a calibration factor which should be fitted to operating data. | ||
</hide><div class="user-show"> | |||
=== Cyclone capacity === | === Cyclone capacity === | ||
</div><hide> | |||
The volumetric capacity of a cyclone at a given operating pressure, <math> | The '''volumetric capacity''' of a cyclone at a given operating pressure, <math>Q_{\rm f}</math> (m<sup>3</sup>/h), is estimated from the pressure-throughput relationship: | ||
:<math> | :<math>Q_{\rm f} = K_{\rm Q0} {D_{\rm c}}^{-0.1} \left ( \dfrac{D_{\rm o}}{D_{\rm c}} \right )^{0.68} \left ( \dfrac{D_{\rm i}}{D_{\rm c}} \right )^{0.45} \left ( \dfrac{L_{\rm c}}{D_{\rm c}} \right )^{0.2} \theta^{-0.1} {D_{\rm c}}^2 \left ( \dfrac{P}{\rho_{\rm p}} \right )^{0.5}</math> | ||
where <math>K_{Q0}</math> is a calibration factor which should be fitted to operating data. | where <math>K_{\rm Q0}</math> is a calibration factor which should be fitted to operating data. | ||
This expression may be used to estimate the number of cyclones required to accept a given total cluster feed flow rate at a fixed pressure, e.g. a process set point. | This expression may be used to estimate the number of cyclones required to accept a given total cluster feed flow rate at a fixed pressure, e.g. a process set point. | ||
Alternatively, the pressure drop arising from a given feed flow rate may be calculated by rearranging the above equation: | Alternatively, the '''pressure drop''' arising from a given feed flow rate may be calculated by rearranging the above equation: | ||
:<math>P = \ | :<math>P = \rho_{\rm p} \left [ {Q_{\rm f}}{{K_{\rm Q0}}^{-1} {D_{\rm c}}^{0.1} \left ( \dfrac{D_{\rm o}}{D_{\rm c}} \right )^{-0.68} \left ( \dfrac{D_{\rm i}}{D_{\rm c}} \right )^{-0.45} \left ( \dfrac{L_{\rm c}}{D_{\rm c}} \right )^{-0.2} \theta^{0.1} {D_{\rm c}}^{-2}} \right ]^2</math> | ||
</hide><div class="user-show"> | |||
=== Volume recovery === | === Volume recovery === | ||
</div><hide> | |||
the volumetric recovery of feed pulp to the underflow stream, <math> | the volumetric recovery of feed pulp to the underflow stream, <math>R_{\rm v}</math> (frac), may be estimated from: | ||
:<math> | :<math>R_{\rm v} = K_{\rm V1} \left ( \dfrac{D_{\rm o}}{D_{\rm c}} \right )^{-0.94} \left ( \dfrac{D_{\rm u}}{D_{\rm c}} \right )^{1.83} \left ( \dfrac{D_{\rm i}}{D_{\rm c}} \right )^{0.25} \left ( \dfrac{L_{\rm c}}{D_{\rm c}} \right )^{0.22} \theta^{-0.24} \left ( \dfrac{P}{\rho_{\rm p} g D_{\rm c}} \right )^{-0.31}</math> | ||
where <math>K_{V1}</math> is a calibration factor which should be fitted to operating data. | where <math>K_{\rm V1}</math> is a calibration factor which should be fitted to operating data. | ||
Note that the water splits to underflow implied by each of the <math> | Note that the water splits to underflow implied by each of the <math>R_{\rm f}</math> and <math>R_{\rm v}</math> expressions may not be in agreement. Therefore, the actual water split to underflow is computed by averaging the values from the <math>R_{\rm f}</math> and <math>R_{\rm v}</math> expressions. {{Nageswararao et al. (2004)}} | ||
</hide><div class="user-show"> | |||
=== Multi-component modelling === | === Multi-component modelling === | ||
</div><hide> | |||
The original Nageswararao model formulation | The original Nageswararao model formulation included a pulp density term, <math>\rho_{\rm p}</math>, in the corrected cut size equation. The pulp may comprise a number of individual ore or mineral components with different solid densities. | ||
Napier-Munn (1996) suggests scaling the corrected cut sizes of individual mineral components within a stream based on solid density:{{Napier-Munn et al. (1996)}} | Napier-Munn (1996) suggests scaling the corrected cut sizes of individual mineral components within a stream based on solid density:{{Napier-Munn et al. (1996)}} | ||
:<math>\dfrac{(d_{50c}) | :<math>\dfrac{(d_{\rm 50c})_{\rm a}}{(d_{\rm 50c})_{\rm b}} = \left [ \dfrac{(\rho_{\rm s})_{\rm b} - \rho_{\rm L}}{(\rho_{\rm s})_{\rm a} - \rho_{\rm L}} \right ]^{0.5}</math> | ||
where <math>a</math> and <math>b</math> indicate different ore/mineral types, <math>\ | where <math>a</math> and <math>b</math> indicate different ore/mineral types, <math>\rho_{\rm s}</math> is solid density (t/m<sup>3</sup>), and <math>\rho_{\rm L}</math> is liquid density (t/m<sup>3</sup>). | ||
Lynch (1977) recommends a value of 1.0 for the exponent in the above equation, representing fully turbulent flow.{{Lynch (1977)}} | Lynch (1977) recommends a value of 1.0 for the exponent in the above equation, representing fully turbulent flow.{{Lynch (1977)}} | ||
The <math>d_{50c}</math> of each ore component in the feed is therefore scaled from the <math>d_{50c}</math> of the combined feed stream as: | The <math>d_{\rm 50c}</math> of each ore component in the feed is therefore scaled from the <math>d_{\rm 50c}</math> of the combined feed stream as: | ||
:<math>(d_{50c})_j = d_{50c} \left [ \dfrac{\ | :<math>(d_{\rm 50c})_j = d_{\rm 50c} \left [ \dfrac{\rho_{\rm s} - \rho_{\rm L}}{(\rho_{\rm s})_j - \rho_{\rm L}} \right ]</math> | ||
where <math>j</math> is the index of the ore component. | where <math>j</math> is the index of the ore component. | ||
| Line 89: | Line 104: | ||
The proposed density correction is applied to generate a separate partition curve for each ore component in the feed. | The proposed density correction is applied to generate a separate partition curve for each ore component in the feed. | ||
</hide><div class="user-show"> | |||
=== Partition metrics === | === Partition metrics === | ||
</div><hide> | |||
{{Model theory (Text, Hydrocyclone, Partition Metrics)}} | {{Model theory (Text, Hydrocyclone, Partition Metrics)}} | ||
</hide><div class="user-show"> | |||
=== Roping === | === Roping === | ||
</div><hide> | |||
{{Model theory (Text, Hydrocyclone, Roping)}} | {{Model theory (Text, Hydrocyclone, Roping)}} | ||
</hide> | |||
== Excel == | == Excel == | ||
| Line 109: | Line 129: | ||
{{Excel (Text, Inputs)}} | {{Excel (Text, Inputs)}} | ||
:<math>Parameters= | :<math>\mathit{Parameters}= | ||
\begin{bmatrix} | \begin{bmatrix} | ||
\text{Pressure control}\\ | \text{Pressure control}\\ | ||
\text{Number of cyclones}\\ | \text{Number of cyclones}\\ | ||
D_{\rm c}\text{ (m)}\\ | |||
D_{\rm i}\text{ (m)}\\ | |||
D_{\rm o}\text{ (m)}\\ | |||
D_{\rm u}\text{ (m)}\\ | |||
L_{\rm c}\text{ (m)}\\ | |||
\theta\text{ (deg.)}\\ | \theta\text{ (deg.)}\\ | ||
P\text{ (kPa)}\\ | P\text{ (kPa)}\\ | ||
K_{D0}\\ | K_{\rm D0}\\ | ||
K_{Q0}\\ | K_{\rm Q0}\\ | ||
K_{V1}\\ | K_{\rm V1}\\ | ||
K_{W1}\\ | K_{\rm W1}\\ | ||
\alpha\\ | \alpha\\ | ||
\beta\\ | \beta\\ | ||
(Q_{\rm M,F})_{\rm L}\text{ (t/h)}\\ | |||
\ | \rho_{\rm L}\text{ (t/m}^{\text{3}}\text{)}\\ | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
Size = \begin{bmatrix} | \mathit{Size} = \begin{bmatrix} | ||
d_{1}\text{ (mm)}\\ | d_{1}\text{ (mm)}\\ | ||
\vdots\\ | \vdots\\ | ||
| Line 136: | Line 156: | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
Feed= \begin{bmatrix} | \mathit{Feed}= \begin{bmatrix} | ||
( | (Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\ | ||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
( | (Q_{\rm M,F})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{nm}\text{ (t/h)}\\ | ||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
OreSG= \begin{bmatrix} | \mathit{OreSG}= \begin{bmatrix} | ||
(\ | (\rho_{\rm S})_1\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_{\rm S})_m\text{ (t/m}^\text{3}\text{)}\\ | ||
\end{bmatrix} | \end{bmatrix} | ||
| Line 153: | Line 173: | ||
* <math>\text{Number of cyclones}</math> is the number of cyclones ''operating'' in a cluster. The number of cyclones is ignored if <math>\text{Pressure control}</math> is ''TRUE'' (the value is returned in the results instead) | * <math>\text{Number of cyclones}</math> is the number of cyclones ''operating'' in a cluster. The number of cyclones is ignored if <math>\text{Pressure control}</math> is ''TRUE'' (the value is returned in the results instead) | ||
* <math>P</math>, the operating pressure, is ignored if <math>\text{Pressure control}</math> is ''FALSE'' (the value is returned in the results instead) | * <math>P</math>, the operating pressure, is ignored if <math>\text{Pressure control}</math> is ''FALSE'' (the value is returned in the results instead) | ||
* <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm) | |||
* <math>m</math> is the number of ore types | * <math>m</math> is the number of ore types | ||
* <math> | * <math>Q_{\rm M,F}</math> is feed solids mass flow rate by size and ore type (t/h) | ||
* <math> | * <math>(Q_{\rm M,F})_{\rm L}</math> is the mass flow feed rate of liquids into the cyclone (t/h) | ||
=== Results === | === Results === | ||
| Line 162: | Line 183: | ||
:<math> | :<math> | ||
mdUnit\_Hydrocyclone\_Nageswararao = | \mathit{mdUnit\_Hydrocyclone\_Nageswararao} = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
\begin{ | \begin{bmatrix} | ||
\text{Number of cyclones}\\ | \text{Number of cyclones}\\ | ||
\text{Qv per cyclone (m}^{\text{3}}\text{/h)}\\ | \text{Qv per cyclone (m}^{\text{3}}\text{/h)}\\ | ||
\text{Qv per cluster (m}^{\text{3}}\text{/h)}\\ | \text{Qv per cluster (m}^{\text{3}}\text{/h)}\\ | ||
C_{\rm V} \text{ (}\%\text{ v/v)}\\ | |||
P\text{ (kPa)}\\ | P\text{ (kPa)}\\ | ||
R_{\rm v}\text{ (frac)}\\ | |||
R_{\rm f}\text{ (frac)}\\ | |||
\text{Water split to OF (frac)}\\ | \text{Water split to OF (frac)}\\ | ||
d_{50c}\text{ (mm)}\\ | d_{\rm 50c}\text{ (mm)}\\ | ||
(Q_{\rm M,OF})_{\rm L}\text{ (t/h)}\\ | |||
(Q_{\rm M,UF})_{\rm L}\text{ (t/h)}\\ | |||
d_{50}\text{ (mm)}\\ | d_{50}\text{ (mm)}\\ | ||
E_{\rm p}\text{ (mm)}\\ | |||
I\\ | I\\ | ||
\text{SPOC }C_{VU}\text{ (v/v)}\\ | \text{SPOC }C_{\rm VU}\text{ (v/v)}\\ | ||
\text{Plitt }M_{SU}\text{ (m}^{3}\text{/h)}\\ | \text{Plitt }M_{\rm SU}\text{ (m}^{3}\text{/h)}\\ | ||
\text{Plitt }\ | \text{Plitt }\Phi_{\rm L}\text{ (v/v)}\\ | ||
\text{Bustamante condition}\\ | \text{Bustamante condition}\\ | ||
\text{Concha condition}\\ | \text{Concha condition}\\ | ||
\end{ | \end{bmatrix} | ||
| Line 200: | Line 221: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
( | (Q_{\rm M,UF})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,UF})_{1m}\text{ (t/h)}\\ | ||
\vdots & \ddots & \vdots\\ | |||
(Q_{\rm M,UF})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,UF})_{nm}\text{ (t/h)}\\ | |||
\end{bmatrix} | |||
& | |||
\begin{bmatrix} | |||
(Q_{\rm M,OF})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,OF})_{1m}\text{ (t/h)}\\ | |||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
( | (Q_{\rm M,OF})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,OF})_{nm}\text{ (t/h)}\\ | ||
\end{bmatrix} | \end{bmatrix} | ||
| Line 208: | Line 237: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
( | (E_{\rm oa})_{11}\text{ (frac)} & \dots & (E_{\rm oa})_{1m}\text{ (frac)}\\ | ||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
( | (E_{\rm oa})_{n1}\text{ (frac)} & \dots & (E_{\rm oa})_{nm}\text{ (frac)}\\ | ||
\end{bmatrix} | \end{bmatrix} | ||
| Line 216: | Line 245: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
(P_{\rm OF})_{1,{\rm All}}\\ | |||
\vdots\\ | \vdots\\ | ||
(P_{\rm OF})_{n,{\rm All}}\\ | |||
\end{bmatrix} | \end{bmatrix} | ||
| Line 224: | Line 253: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
(d_{50c})_1 & \dots & (d_{50c})_m\\ | (d_{\rm 50c})_1 & \dots & (d_{\rm 50c})_m\\ | ||
\beta^*_1 & \dots & \beta^*_m\\ | \beta^*_1 & \dots & \beta^*_m\\ | ||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
| Line 256: | Line 285: | ||
* <math>P</math> is the pressure drop across the cyclone cluster with <math>\text{Number of cyclones}</math> operating at feed rate <math>\text{Qv per cluster}</math>, if <math>\text{Pressure control}</math> = ''FALSE'' (kPa) | * <math>P</math> is the pressure drop across the cyclone cluster with <math>\text{Number of cyclones}</math> operating at feed rate <math>\text{Qv per cluster}</math>, if <math>\text{Pressure control}</math> = ''FALSE'' (kPa) | ||
* <math>\text{Water split to OF}</math> is actual split of liquids to the overflow (frac) | * <math>\text{Water split to OF}</math> is actual split of liquids to the overflow (frac) | ||
* <math> | * <math>(Q_{\rm M,OF})_{\rm L}</math> is the mass flow rate of liquids to the overflow stream (t/h) | ||
* <math>(Q_{\rm M,UF})_{\rm L}</math> is the mass flow rate of liquids to the underflow stream (t/h) | |||
* <math> | * <math>\text{SPOC }C_{\rm VU}</math> is the SPOC roping limit of volume fraction solids in the underflow stream (v/v) | ||
* <math>\text{Plitt }M_{\rm SU}</math> is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m<sup>3</sup>/h) | |||
* <math>\text{Plitt }\Phi_{\rm L}</math> is the Plitt roping limit of volume fraction solids in the underflow stream (v/v) | |||
* <math>\text{SPOC }C_{VU}</math> is the SPOC roping limit of volume fraction solids in the underflow stream (v/v) | |||
* <math>\text{Plitt }M_{SU}</math> is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m<sup>3</sup>/h) | |||
* <math>\text{Plitt }\ | |||
* <math>\text{Bustamante condition}</math> is the underflow discharge type based on the Bustamante geometry limits (''spray'' or ''roping'' discharge) | * <math>\text{Bustamante condition}</math> is the underflow discharge type based on the Bustamante geometry limits (''spray'' or ''roping'' discharge) | ||
* <math>\text{Concha condition}</math> is the underflow discharge type based on the Concha geometry limits (''spray'' or ''roping'' discharge) | * <math>\text{Concha condition}</math> is the underflow discharge type based on the Concha geometry limits (''spray'' or ''roping'' discharge) | ||
* <math>Q_{\rm M,UF}</math> is mass flow rate of solids to the underflow stream (t/h) | |||
* <math>Q_{\rm M,OF}</math> is mass flow rate of solids to the overflow stream (t/h) | |||
* <math>(P_{\rm OF})_{i,{\rm All}}</math> is the actual partition of all particles of size <math>i</math> to the overflow stream, computed as <math>\frac{\sum_{j=1}^m(Q_{\rm M,OF})_{ij}}{\sum_{j=1}^m(Q_{\rm M,F})_{ij}}</math> (frac) | |||
=== Example === | === Example === | ||
| Line 280: | Line 309: | ||
The sections and variable names used in the SysCAD interface are described in detail in the following tables. | The sections and variable names used in the SysCAD interface are described in detail in the following tables. | ||
{{SysCAD (Page, Hydrocyclone, | {{SysCAD (Page, Hydrocyclone, DLL*Hydrocyclone)}} | ||
==== Cyclone page ==== | ==== Cyclone page ==== | ||
| Line 286: | Line 315: | ||
The Cyclone page is used to specify the input parameters for the hydrocyclone model. | The Cyclone page is used to specify the input parameters for the hydrocyclone model. | ||
{{ | {{SysCAD (Text, Table Header)}} | ||
|- | |- | ||
! colspan="3" style="text-align:left;" |''Nageswararao'' | ! colspan="3" style="text-align:left;" |''Nageswararao'' | ||
{{SysCAD (Text, Help Link)}} | |||
|- | |- | ||
|PressureControl | |PressureControl | ||
|CheckBox | |CheckBox | ||
|If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate. | |If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate. | ||
|- | |||
|DensityCorrection | |||
|CheckBox | |||
|If enabled, the density of individual species is used to compute separate <math>d_{50c}</math> values, as described in [[Hydrocyclone (Nageswararao)#Multi-component modelling|Multi-component modelling]] above. | |||
|- | |- | ||
! colspan="3" style="text-align:left;" |''Dimensions'' | ! colspan="3" style="text-align:left;" |''Dimensions'' | ||
| Line 355: | Line 391: | ||
|'Fish hook' parameter of the Whiten-Beta efficiency curve equation. | |'Fish hook' parameter of the Whiten-Beta efficiency curve equation. | ||
{{SysCAD (Text, Hydrocyclone, Liquids)}} | {{SysCAD (Text, Hydrocyclone, Liquids)|method=0}} | ||
|- | |- | ||
! colspan="3" style="text-align:left;" |''Results'' | ! colspan="3" style="text-align:left;" |''Results'' | ||
|- | |- | ||
|ClusterQv | |ClusterQv / Cluster.Qv | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
|Volumetric flow rate of feed to the cyclone cluster (i.e. total flow). | |Volumetric flow rate of feed to the cyclone cluster (i.e. total flow). | ||
|- | |- | ||
|CycloneQv | |CycloneQv / Cyclone.Qv | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
|Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow). | |Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow). | ||
|- | |- | ||
|OperatingPressure | |OperatingPressure / P | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
|Pressure drop across the cyclone. | |Pressure drop across the cyclone. | ||
|- | |- | ||
|Cv | |VolFracSolids / Cv | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
|Volume fraction of solids in feed stream. | |Volume fraction of solids in feed stream. | ||
| Line 388: | Line 424: | ||
|Fraction of feed slurry volume recovered to underflow stream. | |Fraction of feed slurry volume recovered to underflow stream. | ||
|- | |- | ||
|WaterSplitToOF | |WaterSplitToOF / OF.LiqSplit | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
|Actual fraction of feed liquids recovered to overflow stream. | |Actual fraction of feed liquids recovered to overflow stream. | ||
| Line 404: | Line 440: | ||
|} | |} | ||
{{SysCAD (Page, Hydrocyclone, Partition)}} | {{SysCAD (Page, Hydrocyclone, Partition)|ActionU=Partition|ActionL=partition|DestinationU=Overflow|DestinationL=overflow|UnitL=cyclone}} | ||
{{SysCAD (Page, Hydrocyclone, Roping)}} | {{SysCAD (Page, Hydrocyclone, Roping)}} | ||
{{SysCAD (Page, About)}} | {{SysCAD (Page, About)}} | ||
==== Additional notes ==== | |||
{{SysCAD (Text, No PSD Splits)|gasstream=overflow}} | |||
== See also == | == See also == | ||
| Line 414: | Line 454: | ||
* [[Hydrocyclone (Plitt)]] | * [[Hydrocyclone (Plitt)]] | ||
* [[Hydrocyclone (Narasimha-Mainza)]] | * [[Hydrocyclone (Narasimha-Mainza)]] | ||
== External links == | |||
* [https://help.syscad.net/Met_Dynamics_-_Hydrocyclone Met Dynamics - Hydrocyclone (help.syscad.net)] | |||
== References == | == References == | ||
Latest revision as of 13:30, 1 May 2025
Description
This article describes the Nageswararao model for hydrocyclone size classification.[1]
Model theory
Efficiency curve
Corrected cut size
Liquids recovery
Cyclone capacity
Volume recovery
Multi-component modelling
Partition metrics
Roping
Excel
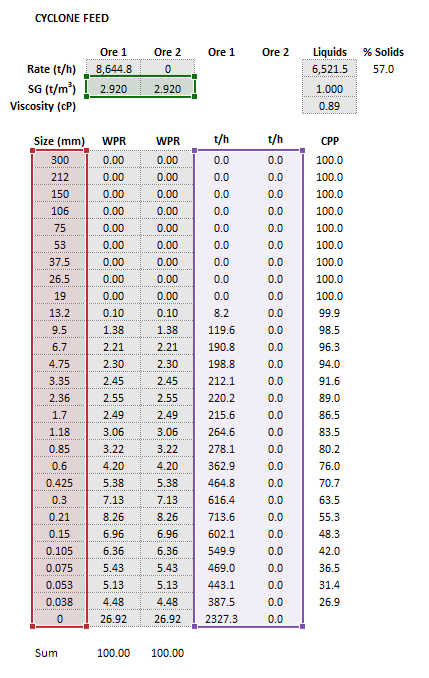
The Nageswararao hydrocyclone model may be invoked from the Excel formula bar with the following function call:
=mdUnit_Hydrocyclone_Nageswararao(Parameters as Range, Size as Range, Feed as Range, OreSG Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:
where:
- indicates whether the number of cyclones required at the given feed flow rate and pressure set point is returned (TRUE) or the operating pressure at the given feed flowrate and number of cyclones is returned (FALSE)
- is the number of cyclones operating in a cluster. The number of cyclones is ignored if is TRUE (the value is returned in the results instead)
- , the operating pressure, is ignored if is FALSE (the value is returned in the results instead)
- is the size of the square mesh interval that feed mass is retained on (mm)
- is the number of ore types
- is feed solids mass flow rate by size and ore type (t/h)
- is the mass flow feed rate of liquids into the cyclone (t/h)
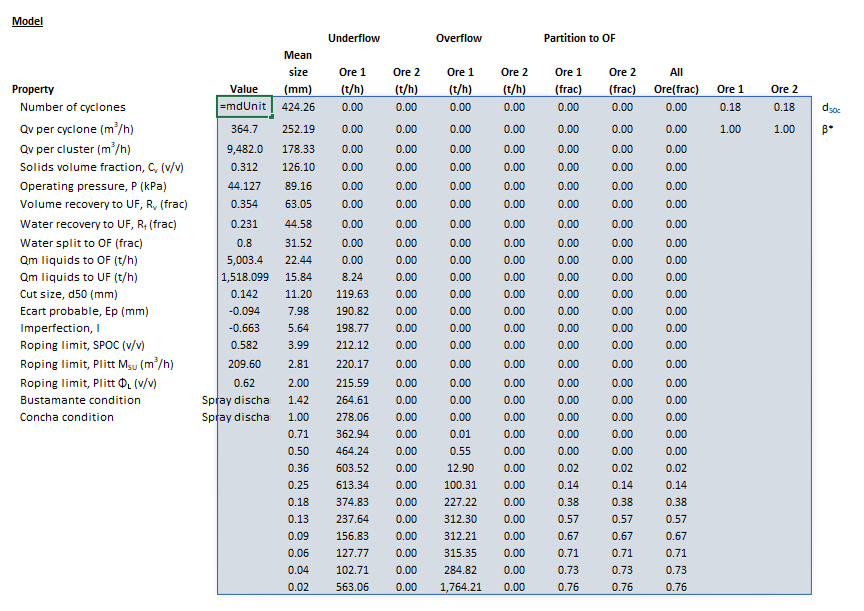
Results
The results are displayed in Excel as an array corresponding to the matrix notation below:
where:
- is the number of cyclones required at the given and operating pressure , if = TRUE
- is the volumetric feed flow rate per cyclone (m3/h)
- is the total volumetric feed flow rate to the cluster of cyclones (m3/h)
- is the pressure drop across the cyclone cluster with operating at feed rate , if = FALSE (kPa)
- is actual split of liquids to the overflow (frac)
- is the mass flow rate of liquids to the overflow stream (t/h)
- is the mass flow rate of liquids to the underflow stream (t/h)
- is the SPOC roping limit of volume fraction solids in the underflow stream (v/v)
- is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m3/h)
- is the Plitt roping limit of volume fraction solids in the underflow stream (v/v)
- is the underflow discharge type based on the Bustamante geometry limits (spray or roping discharge)
- is the underflow discharge type based on the Concha geometry limits (spray or roping discharge)
- is mass flow rate of solids to the underflow stream (t/h)
- is mass flow rate of solids to the overflow stream (t/h)
- is the actual partition of all particles of size to the overflow stream, computed as (frac)
Example
The images below show the selection of input arrays and output results in the Excel interface.
SysCAD
The sections and variable names used in the SysCAD interface are described in detail in the following tables.
MD_Hydrocyclone page
The first tab page in the access window will have this name.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Tag | Display | This name tag may be modified with the change tag option. |
| Condition | Display | OK if no errors/warnings, otherwise lists errors/warnings. |
| ConditionCount | Display | The current number of errors/warnings. If condition is OK, returns 0. |
| GeneralDescription / GenDesc | Display | This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.
If this field is blank, then SysCAD will display the unit class ID. |
| Requirements | ||
| On | CheckBox | This enables the unit. If this box is not checked, then the MassFracToUF option appears below. |
| MassFracToUF | Input | Only appears if the On field above is not checked. Specifies the fraction of feed mass that reports to the underflow stream when the model is off. |
| Method | Partition (User) | The partition to overflow for each size interval is defined by the user. Different values can be used for different solids. |
| Partition (Reid-Plitt) | The partition to overflow for each size interval is defined by a Reid-Plitt efficiency curve. Different parameters can be used for different solids. | |
| Partition (Whiten-Beta) | The partition to overflow for each size interval is defined by a Whiten-Beta efficiency curve. Different parameters can be used for different solids. | |
| Nageswararao | The Nageswararao model is used to determine the partition of solids to underflow and overflow for each size interval. | |
| Narasimha-Mainza (2014) | The Narasimha-Mainza (2014) model is used to determine the partition of solids to underflow and overflow for each size interval. | |
| Narasimha-Mainza (Multi) | The Narasimha-Mainza (Multi) model is used to determine the partition of solids to underflow and overflow for each size interval. | |
| Plitt | The Plitt model is used to determine the partition of solids to underflow and overflow for each size interval. | |
| RopingCalcs | CheckBox | Show addition calculations that predict the onset of cyclone underflow roping. |
| Options | ||
| ShowQFeed | CheckBox | QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream. |
| ShowQOF | CheckBox | QOF and associated tab pages (eg Sp) will become visible, showing the properties of the overflow stream. |
| ShowQUF | CheckBox | QUF and associated tab pages (eg Sp) will become visible, showing the properties of the underflow stream. |
| SizeForPassingFracCalc | Input | Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section. |
| FracForPassingSizeCalc | Input | Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section. |
| Stream Summary | ||
| MassFlow / Qm | Display | The total mass flow in each stream. |
| SolidMassFlow / SQm | Display | The Solids mass flow in each stream. |
| LiquidMassFlow / LQm | Display | The Liquid mass flow in each stream. |
| VolFlow / Qv | Display | The total Volume flow in each stream. |
| Temperature / T | Display | The Temperature of each stream. |
| Density / Rho | Display | The Density of each stream. |
| SolidFrac / Sf | Display | The Solid Fraction in each stream. |
| LiquidFrac / Lf | Display | The Liquid Fraction in each stream. |
| Passing | Display | The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream. |
| Passes | Display | The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction. |
Cyclone page
The Cyclone page is used to specify the input parameters for the hydrocyclone model.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Nageswararao | ||
| HelpLink | Opens a link to this page using the system default web browser. Note: Internet access is required. | |
| PressureControl | CheckBox | If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate. |
| DensityCorrection | CheckBox | If enabled, the density of individual species is used to compute separate values, as described in Multi-component modelling above. |
| Dimensions | ||
| NumberCyclones / NumCyclones | Input | The number of operating cyclone units in the cluster. |
| CycloneDiameter / Dc | Input | Diameter of the cyclone. |
| InletDiameter / Di | Input | Diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet. |
| CycloneDiameter / Dc | Input | Diameter of the cyclone. |
| OverflowDiameter / Do | Input | Diameter of the vortex finder (overflow). |
| UnderflowDiameter / Du | Input | Diameter of the apex/spigot (underflow). |
| CylSectLength / Lc | Input | Length of the cylindrical section of the cyclone. |
| ConeFullAngle / Theta | Input | Full angle of the cone section of the cyclone. |
| Parameters | ||
| KD0 | Input | Calibration factor for the d50c equation. |
| KQ0 | Input | Calibration factor for the pressure-flowrate equation |
| KV1 | Input | Calibration factor for the volumetric pulp recovery to underflow equation. |
| KW1 | Input | Calibration factor for the liquids recovery to underflow equation. |
| Alpha | Input | Sharpness parameter of the Whiten-Beta efficiency curve equation. |
| Beta | Input | 'Fish hook' parameter of the Whiten-Beta efficiency curve equation. |
| Liquids | ||
| LiquidsSeparMethod | Split To UF (User) | Liquids are split to underflow by a user-defined fraction of liquids in the feed. |
| Split To UF (Model) | Liquids are split to underflow by a fraction computed by the associated model. | |
| UF Solids Fraction | Sufficient liquids mass is recovered to the underflow stream to yield the user-defined underflow solids mass fraction value (if possible). | |
| UF Liquids Fraction | Sufficient liquids mass is recovered to the underflow stream to yield the user-defined underflow liquids mass fraction value (if possible). | |
| UFSolidsFracReqd / UF.SfReqd | Input | Required value of the mass fraction of solids in the underflow stream. Only visible if UF Solids Fraction is selected. |
| UFLiquidsFracReqd / UF.LfReqd | Input | Required value of the mass fraction of liquids in the underflow stream. Only visible if UF Liquids Fraction is selected. |
| LiqSplitToUF / UF.LiqSplit | Input/Display | The fraction of liquids recovered to underflow. |
| Results | ||
| ClusterQv / Cluster.Qv | Display | Volumetric flow rate of feed to the cyclone cluster (i.e. total flow). |
| CycloneQv / Cyclone.Qv | Display | Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow). |
| OperatingPressure / P | Display | Pressure drop across the cyclone. |
| VolFracSolids / Cv | Display | Volume fraction of solids in feed stream. |
| lambda | Display | Hindered settling factor. |
| Rf | Display | Fraction of feed liquids recovered to underflow stream. |
| Rv | Display | Fraction of feed slurry volume recovered to underflow stream. |
| WaterSplitToOF / OF.LiqSplit | Display | Actual fraction of feed liquids recovered to overflow stream. |
| d50 | Display | The separation size, d50, of all solid particles in the feed. |
| EcartProbable / Ep | Display | The value of the Ecart Probable of the separation. |
| Imperfection / I | Display | The value of the Imperfection of the separation. |
| d50c | Display | Value of the corrected d50c, per species. |
| Beta* | Display | Value of , per species. |
Partition page
The Partition page is used to display (or specify) the partition by species/component/element/individual phase and size values.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Distribution | ||
| Name | Display | Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream. |
| IntervalCount | Display | Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream. |
| SpWithPSDCount | Display | Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality. |
| Partition | ||
| Method | Model / User | Select model-calculated or user-defined partition to separate each solids species type. |
| Density | Display | Density of each solid species. |
| Size | Display | Size of each interval in mesh series. |
| MeanSize | Display | Geometric mean size of each interval in mesh series.
|
| All (All column) | Display |
|
| Partition | Display |
|
| All (All row, All column) | Display |
|
| All (All row, per species) | Display |
|
| CmpPartition | ||
| Components | Hides or shows component partition table. | |
| Size | Display | Size of each interval in mesh series. |
| MeanSize | Display | Geometric mean size of each interval in mesh series. |
| All (All column) | Display |
|
| CmpPartition | Display |
|
| All (All row, All column) | Display |
|
| All (All row, per component) | Display |
|
| ElePartition | ||
| Elements | Hides or shows element partition table. | |
| Size | Display | Size of each interval in mesh series. |
| MeanSize | Display | Geometric mean size of each interval in mesh series. |
| All (All column) | Display |
|
| ElePartition | Display |
|
| All (All row, All column) | Display |
|
| All (All row, per element) | Display |
|
| IPhPartition | ||
| IPhases | Hides or shows individual phases partition table. | |
| Size | Display | Size of each interval in mesh series. |
| MeanSize | Display | Geometric mean size of each interval in mesh series. |
| All (All column) | Display |
|
| IPhPartition | Display |
|
| All (All row, All column) | Display |
|
| All (All row, per individual phase) | Display |
|
Roping page
This page displays the results for hydrocyclone roping limit calculations. The page is only visible if Roping is selected on the MD_Hydrocyclone page.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Roping | ||
| Underflow | ||
| SolidsVolFlow / SQv | Display | Volumetric flow rate of solids in cyclone underflow stream. |
| Plitt.MSu | Display | Plitt's volumetric flow rate of solids in cyclone underflow roping limit. |
| SolidsVolFrac / Svf | Display | Volume fraction of solids in the cyclone underflow stream. |
| SPOC | Display | SPOC volume fraction of solids in the cyclone underflow roping limit. |
| Plitt.phiL | Display | Plitt's volume fraction of solids in the cyclone underflow roping limit. |
| Geometry | ||
| BCondition | Display | Text string describing the spray/roping condition of the cyclone based on Bustamante's geometry limits. |
| CCondition | Display | Text string describing the spray/roping condition of the cyclone based on the Concha et al. geometry limits. |
About page
This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| About | ||
| HelpLink | Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required. | |
| Information | Copies Product and License information to the Windows clipboard. | |
| Product | ||
| Name | Display | Met Dynamics software product name |
| Version | Display | Met Dynamics software product version number. |
| BuildDate | Display | Build date and time of the Met Dynamics Models SysCAD Add-On. |
| License | ||
| File | This is used to locate a Met Dynamics software license file. | |
| Location | Display | Type of Met Dynamics software license or file name and path of license file. |
| SiteCode | Display | Unique machine identifier for license authorisation. |
| ReqdAuth | Display | Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime. |
| Status | Display | License status, LICENSE_OK indicates a valid license, other messages report licensing errors. |
| IssuedTo | Display | Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to. |
| ExpiryDate | Display | Only visible if Met Dynamics license file is used. License expiry date. |
| DaysLeft | Display | Only visible if Met Dynamics license file is used. Days left before the license expires. |
Additional notes
- Solid species that do not possess a particle size distribution property are split according to the overall mass split of the default particle size distribution species selected in the SysCAD Project Configuration.
- If the default particle size distribution species is not present in the unit feed, the overall split of all other species with particle size distributions combined is used, as determined by the model.
- Gas phase species report directly to the overflow stream without split.
See also
External links
References
- ↑ Napier-Munn, T.J., Morrell, S., Morrison, R.D. and Kojovic, T., 1996. Mineral comminution circuits: their operation and optimisation. Julius Kruttschnitt Mineral Research Centre, Indooroopilly, QLD.