Ball Mill (Overfilling): Difference between revisions
imported>Scott.Munro mNo edit summary |
imported>Scott.Munro m (→Model theory) |
||
| Line 8: | Line 8: | ||
<hide> | <hide> | ||
</hide><div class="user-show"> | |||
=== Shi method === | === Shi method === | ||
</div><hide> | |||
[[File:BallMillOverfilling1.png|thumb|450px|Figure 1. Overflow discharge tumbling mill profile showing Shi's assumed charge and slurry pool areas.]] | [[File:BallMillOverfilling1.png|thumb|450px|Figure 1. Overflow discharge tumbling mill profile showing Shi's assumed charge and slurry pool areas.]] | ||
| Line 24: | Line 26: | ||
Estimating the slurry volume in areas A-C requires definition of the simplified charge geometry and slurry pool level for the mill in question. | Estimating the slurry volume in areas A-C requires definition of the simplified charge geometry and slurry pool level for the mill in question. | ||
</hide><div class="user-show"> | |||
==== Charge position ==== | ==== Charge position ==== | ||
</div><hide> | |||
The simplified charge geometry is defined by three parameters: | The simplified charge geometry is defined by three parameters: | ||
| Line 80: | Line 84: | ||
:<math>\bar r = \frac{r_{\rm m}}{2} \left [ 1 + \left ( 1 - \frac{2 \pi J_{\rm t}}{2 \pi + \theta_{\rm s} - \theta_{\rm t}} \right )^{0.5} \right ]</math> | :<math>\bar r = \frac{r_{\rm m}}{2} \left [ 1 + \left ( 1 - \frac{2 \pi J_{\rm t}}{2 \pi + \theta_{\rm s} - \theta_{\rm t}} \right )^{0.5} \right ]</math> | ||
</hide><div class="user-show"> | |||
==== Slurry hold-up below pool level ==== | ==== Slurry hold-up below pool level ==== | ||
</div><hide> | |||
The volume of slurry held up below the pool level in areas B and C, <math>V_1</math> (m<sup>3</sup>), is: | The volume of slurry held up below the pool level in areas B and C, <math>V_1</math> (m<sup>3</sup>), is: | ||
| Line 135: | Line 141: | ||
:<math>\varepsilon_{\rm d} = 0.4 + 0.228 \left [ 1 - \exp \left (-0.315\dfrac{\phi}{J_{\rm t}} \right) \right ]</math> | :<math>\varepsilon_{\rm d} = 0.4 + 0.228 \left [ 1 - \exp \left (-0.315\dfrac{\phi}{J_{\rm t}} \right) \right ]</math> | ||
</hide><div class="user-show"> | |||
==== Slurry hold up above pool level ==== | ==== Slurry hold up above pool level ==== | ||
</div><hide> | |||
The volume of slurry held up in the grinding media interstices above the slurry pool level in area A, <math>V_2</math> (m<sup>3</sup>), is: | The volume of slurry held up in the grinding media interstices above the slurry pool level in area A, <math>V_2</math> (m<sup>3</sup>), is: | ||
| Line 145: | Line 153: | ||
:<math>S_{\rm ball\,above\,pool} = 0.5 (\theta_{\rm s} + \alpha)({R_{\rm m}}^2 - {R_{\rm t}}^2)</math> | :<math>S_{\rm ball\,above\,pool} = 0.5 (\theta_{\rm s} + \alpha)({R_{\rm m}}^2 - {R_{\rm t}}^2)</math> | ||
</hide><div class="user-show"> | |||
==== Residence time and overfilling ==== | ==== Residence time and overfilling ==== | ||
</div><hide> | |||
The total volume of slurry hold up in the mill is <math>V_{\rm total}=V_1+V_2</math> (m<sup>3</sup>). | The total volume of slurry hold up in the mill is <math>V_{\rm total}=V_1+V_2</math> (m<sup>3</sup>). | ||
| Line 171: | Line 181: | ||
The maximum volumetric flow rate of the mill, <math>Q_{\rm Max}</math> (m<sup>3</sup>/s), at the residence time limit <math>t_{\rm Limit}</math> may be back-calculated using the above relations. However, as the height of slurry above the trunnion lip (<math>h</math>), and hence residence time (<math>t_{\rm Res}</math>), is a function of flow rate, no analytical solution is available and a numerical method is required for computation. | The maximum volumetric flow rate of the mill, <math>Q_{\rm Max}</math> (m<sup>3</sup>/s), at the residence time limit <math>t_{\rm Limit}</math> may be back-calculated using the above relations. However, as the height of slurry above the trunnion lip (<math>h</math>), and hence residence time (<math>t_{\rm Res}</math>), is a function of flow rate, no analytical solution is available and a numerical method is required for computation. | ||
</hide><div class="user-show"> | |||
=== Arbiter method === | === Arbiter method === | ||
</div><hide> | |||
Based on an analysis of industrial ball mills at five operations, Arbiter (1991) postulated that the axial velocity of pulp through a mill should be less than 2.2% of the mill's tangential velocity. The ''Arbiter Flow Number'', <math>N_{\rm q}</math>, is defined as the ratio of axial to tangential velocity and is determined from: | Based on an analysis of industrial ball mills at five operations, Arbiter (1991) postulated that the axial velocity of pulp through a mill should be less than 2.2% of the mill's tangential velocity. The ''Arbiter Flow Number'', <math>N_{\rm q}</math>, is defined as the ratio of axial to tangential velocity and is determined from: | ||
| Line 188: | Line 200: | ||
Overfilling may be a risk if the actual volumetric flow rate to/from the mill approaches or exceeds <math>Q_{N_{\rm q}}</math>. | Overfilling may be a risk if the actual volumetric flow rate to/from the mill approaches or exceeds <math>Q_{N_{\rm q}}</math>. | ||
</hide> | </hide> | ||
Latest revision as of 06:44, 1 May 2025
Description
This article describes several methods for estimating the maximum volumetric flow capacity of an overflow ball mill, including the Shi (2016) and Arbiter (1991) approaches.[1][2]
Model theory
Shi method
Charge position
Slurry hold-up below pool level
Slurry hold up above pool level
Residence time and overfilling
Arbiter method
Excel
Shi method
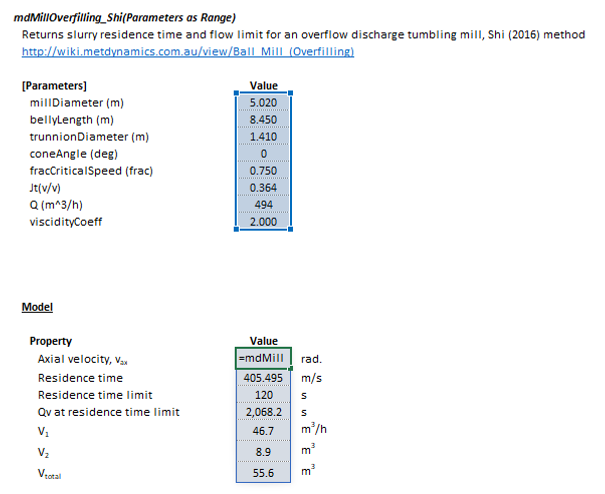
The Shi overflow discharge ball mill overfilling model may be invoked from the Excel formula bar with the following function call:
=mdMillOverfilling_Shi(Parameters as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:
|
|
Arbiter method
The Arbiter overflow discharge ball mill overfilling model may be invoked from the Excel formula bar with the following function call:
=mdMillOverfilling_Arbiter(Parameters as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:
|
|
SysCAD
The Ball Mill Overfilling Indicator model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.