Dense Medium Drum (Baguley): Difference between revisions
imported>Scott.Munro (Created page with "== Description == This article describes the Baguley and Napier-Munn (1996) model for a dense medium drum.{{Baguley and Napier-Munn (1996)}} == Model theory == {{Under construction|section}} == Excel == {{Under construction|section}} == SysCAD == {{Under construction|section}} == See also == * Flotation Cell (Savassi) == References == Category:Excel Category:SysCAD Category:Dynamic") |
imported>Scott.Munro m (→SysCAD) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Description == | == Description == | ||
This article describes the Baguley and Napier-Munn (1996) model for | This article describes the Baguley and Napier-Munn (1996) model for dense medium drums or bath-type separators.{{Baguley and Napier-Munn (1996)}} | ||
== Model theory == | == Model theory == | ||
{{ | {{Restricted content}} | ||
<hide> | |||
[[File:DenseMediumBaguley4.png|thumb|450px|Figure 1. Example of the partition curves generated by the Baguley dense medium drum model (lines) for an industrial data set (markers) (after Baguley, 1988.{{Baguley (1988)}}). Chart series represent density classes.]] | |||
[[File:DenseMediumBaguley5.png|thumb|450px|Figure 2. Example of the partition curves generated by the Baguley dense medium drum model (lines) for the same industrial data set (markers) as Figure 1 (after Baguley, 1988.{{Baguley (1988)}}). Chart series represent size intervals.]] | |||
Baguley and Napier-Munn (1996) proposed a model of dense-medium drum separators where the partitioning behaviour is related to the hydrodynamic properties of particles, such as terminal velocity in a fluid.{{Baguley and Napier-Munn (1996)}} | |||
An empirical function is adopted for the fraction of feed particles reporting to the sinks stream, <math>P</math> (frac): | |||
:<math> | |||
P_{ij} = | |||
\begin{cases} | |||
\left [ 1 - (V_{100} - V_{{\rm t}_{ij}})^2 \right]^x & V_{\rm t} < V_{100}\\ | |||
1 & V_{\rm t} \geq V_{100} | |||
\end{cases} | |||
</math> | |||
where particle size effects are incorporated via the <math>x</math> term: | |||
:<math>\ln(x) = \dfrac{A}{{\bar d_i}^2} + B</math> | |||
and: | |||
* <math>i</math> is the index of the size interval, <math>i = \{1,2,\dots,q\}</math>, <math>q</math> is the number of size intervals | |||
* <math>j</math> is the index of the density class, <math>j = \{1,2,\dots,m\}</math>, <math>m</math> is the number of density classes | |||
* <math>V_{100}</math> is the terminal velocity of particles of which 100% report to sinks (m/s) | |||
* <math>V_{\rm t}</math> is the terminal velocity of particles (m/s) | |||
* <math>A</math> is a coefficient of the size expression (-) | |||
* <math>B</math> is constant of the size expression (-) | |||
* <math>\bar d_{i}</math> is the [[Conversions|geometric mean size]] of particles in size interval <math>i</math> (mm) | |||
In order to compute the terminal velocity, the series of expressions described below are used. | |||
The dimensionless terminal velocity, <math>V_{\rm t}^* </math>, is computed for each particle size (<math>i</math>) and density class (<math>j</math>) from: | |||
:<math>V_{\rm t}^* = \dfrac{{\delta_0}^2}{4d^*} \left [ \left ( 1 + \dfrac{4{d^*}^{1.5}}{{C_0}^{0.5} {\delta_0}^2} \right )^{0.5} - 1 \right ]^2</math> | |||
where <math>d^*</math> is the dimensionless particle size computed from: | |||
:<math>d^* = \dfrac{\bar d}{p}</math> | |||
and <math>\bar d</math> is the [[Conversions|geometric mean size]] of particles in a size interval (with units of m in the <math>d^*</math> equation). | |||
The particle-fluid characteristic size parameter, <math>p</math>, is: | |||
:<math>p = \left ( \dfrac{3 \mu^2}{4 (\Delta \rho) \rho_{\rm m} g} \right )^{\frac{1}{3}}</math> | |||
where: | |||
* <math>\mu</math> is the apparent equivalent Newtonian medium viscosity (Pa.s) | |||
* <math>\Delta\rho</math> is density difference between a particle and the medium (kg/m<sup>3</sup>) | |||
* <math>\rho_{\rm m}</math> is medium density (kg/m<sup>3</sup>) | |||
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>) | |||
The shape-dependent parameters <math>C_0</math> and <math>\delta_0</math> are calculated from: | |||
:<math>\ln C_0 = -5.99k + 1.95</math> | |||
:<math>\delta_0 = 9.97k + 2.94</math> | |||
where <math>k</math> is a particle shape coefficient, assumed to be 0.225 for spheres. | |||
Finally, the particle terminal velocity, <math>v_{\rm t}</math> (m/s), is computed from: | |||
:<math>V_{\rm t} = V_{\rm t}^* q</math> | |||
where the particle-fluid characteristic velocity parameter, <math>q</math>, is: | |||
:<math>q = \left ( \dfrac{4 (\Delta \rho) \mu g}{3 {\rho_{\rm m}}^2} \right )^{\frac{1}{3}}</math> | |||
</hide> | |||
{{Model theory (Text, Gravity Concentrator, Partition Metrics)}} | |||
== Excel == | == Excel == | ||
{{ | The Baguley dense medium drum model may be invoked from the Excel formula bar with the following function call: | ||
<syntaxhighlight lang="vb">=mdUnit_DMDrum_Baguley(Parameters as Range, Size as Range, Density As Range, Feed as Range)</syntaxhighlight> | |||
{{Excel (Text, Help, No Arguments)}} | |||
=== Inputs === | |||
{{Excel (Text, Inputs)}} | |||
:<math>\mathit{Parameters} = | |||
\begin{bmatrix} | |||
\rho_{\rm m}\text{ (t/m}^{\text{3}}\text{)}\\ | |||
\mu\text{ (mPa.s)}\\ | |||
k\\ | |||
V_{100}\text{ (m/s)}\\ | |||
A\\ | |||
B\\ | |||
\end{bmatrix},\;\;\;\;\;\; | |||
\mathit{Size} = \begin{bmatrix} | |||
d_{1}\text{ (mm)}\\ | |||
\vdots\\ | |||
d_n\text{ (mm)}\\ | |||
\end{bmatrix},\;\;\;\;\;\; | |||
\mathit{Feed} = \begin{bmatrix} | |||
(Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\ | |||
\vdots & \ddots & \vdots\\ | |||
(Q_{\rm M,F})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{nm}\text{ (t/h)}\\ | |||
\end{bmatrix},\;\;\;\;\;\; | |||
\mathit{Density}= \begin{bmatrix} | |||
(\rho_{\rm s})_1\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_{\rm s})_m\text{ (t/m}^\text{3}\text{)}\\ | |||
\end{bmatrix} | |||
</math> | |||
where: | |||
* <math>n</math> is the number of size intervals | |||
* <math>m</math> is the number of density classes | |||
* <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm) | |||
* <math>Q_{\rm M,F}</math> is feed solids mass flow rate by size and ore type (t/h) | |||
* <math>\rho_{\rm S}</math> is the particle density (t/m<sup>3</sup>) | |||
=== Results === | |||
The results are displayed in Excel as an array corresponding to the matrix notation below: | |||
:<math> | |||
\mathit{mdUnit\_DMDrum\_Baguley} = | |||
\begin{bmatrix} | |||
\begin{array}{c} | |||
\begin{bmatrix} | |||
P_{\rm All}\text{ (frac)}\\ | |||
\rho_{50}\text{ (t/m}^3\text{)}\\ | |||
E_{\rm p}\text{ (t/m}^3\text{)}\\ | |||
I\text{ (-)}\\ | |||
\end{bmatrix} | |||
\end{array} | |||
\begin{array}{cccccccc} | |||
\begin{bmatrix} | |||
\bar d_1\text{ (mm)}\\ | |||
\vdots\\ | |||
\bar d_n\text{ (mm)} | |||
\end{bmatrix} | |||
& | |||
\begin{bmatrix} | |||
(Q_{\rm M,SK})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,SK})_{1m}\text{ (t/h)}\\ | |||
\vdots & \ddots & \vdots\\ | |||
(Q_{\rm M,SK})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,SK})_{nm}\text{ (t/h)}\\ | |||
\end{bmatrix} | |||
& | |||
\begin{bmatrix} | |||
(Q_{\rm M,FT})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,FT})_{1m}\text{ (t/h)}\\ | |||
\vdots & \ddots & \vdots\\ | |||
(Q_{\rm M,FT})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,FT})_{nm}\text{ (t/h)}\\ | |||
\end{bmatrix} | |||
& | |||
\begin{bmatrix} | |||
P_{11}\text{ (frac)} & \dots & P_{1m}\text{ (frac)}\\ | |||
\vdots & \ddots & \vdots\\ | |||
P_{n1}\text{ (frac)} & \dots & P_{nm}\text{ (frac)}\\ | |||
\end{bmatrix} | |||
& | |||
\begin{bmatrix} | |||
P_{1,{\rm All}}\text{ (frac)}\\ | |||
\vdots\\ | |||
P_{n,{\rm All}}\text{ (frac)}\\ | |||
\end{bmatrix} | |||
& | |||
\begin{array}{c} | |||
\begin{bmatrix} | |||
P_{{\rm All}, 1}\text{ (frac)} & \dots & P_{{\rm All}, m}\text{ (frac)}\\ | |||
\end{bmatrix} | |||
\\ | |||
\\ | |||
\\ | |||
\end{array} | |||
& | |||
\begin{bmatrix} | |||
(\rho_{50})_1\text{ (t/m}^3\text{)}\\ | |||
\vdots\\ | |||
(\rho_{50})_n\text{ (t/m}^3\text{)}\\ | |||
\end{bmatrix} | |||
& | |||
\begin{bmatrix} | |||
(E_{\rm p})_1\text{ (t/m}^3\text{)}\\ | |||
\vdots\\ | |||
(E_{\rm p})_n\text{ (t/m}^3\text{)}\\ | |||
\end{bmatrix} | |||
\end{array} | |||
\end{bmatrix} | |||
</math> | |||
where: | |||
* <math>Q_{\rm M,SK}</math> is mass flow rate of solids to the sinks stream (t/h) | |||
* <math>Q_{\rm M,FT}</math> is mass flow rate of solids to the floats stream (t/h) | |||
* <math>P_{\rm All}</math> is the actual partition of all mass to the sinks stream, computed as <math>\frac{\sum_{i=1}^n\sum_{j=1}^m(Q_{\rm M,SK})_{ij}}{\sum_{i=1}^n\sum_{j=1}^m(Q_{\rm M,F})_{ij}}</math> (frac) | |||
* <math>P_{i,{\rm All}}</math> is the actual partition of all particles of size <math>i</math> to the sinks stream, computed as <math>\frac{\sum_{j=1}^m(Q_{\rm M,SK})_{ij}}{\sum_{j=1}^m(Q_{\rm M,F})_{ij}}</math> (frac) | |||
* <math>P_{{\rm All},i}</math> is the actual partition of all particles of density class <math>j</math> to the sinks stream, computed as <math>\frac{\sum_{i=1}^n(Q_{\rm M,SK})_{ij}}{\sum_{i=1}^n(Q_{\rm M,F})_{ij}}</math> (frac) | |||
=== Example === | |||
The images below show the selection of input arrays and output results in the Excel interface. | |||
{| | |||
|- style="vertical-align:top;" | |||
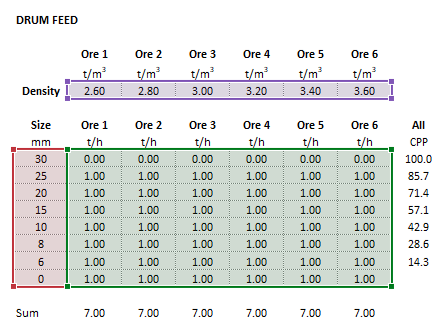
| [[File:DenseMediumBaguley1.png|left|frame|Figure 3. Example showing the selection of the '''Parameters''' (blue frame) array in Excel.]]|| [[File:DenseMediumBaguley2.png|left|frame|Figure 4. Example showing the selection of the '''Size''' (red frame), '''Feed''' (green frame) and '''Density''' (purple frame) arrays in Excel.]] | |||
|} | |||
{| | |||
|- style="vertical-align:top;" | |||
| [[File:DenseMediumBaguley3.png|left|frame|Figure 5. Example showing the outline of the '''Results''' (light blue frame) array in Excel.]] | |||
|} | |||
== SysCAD == | == SysCAD == | ||
{{ | {{SysCAD (Page, Dense Medium, DLL*DenseMedium)|ViscosityModel=true}} | ||
==== Drum page ==== | |||
The Drum page is used to specify the required model method and associated input parameters. | |||
{{SysCAD (Text, Table Header)}} | |||
|- | |||
! colspan="3" style="text-align:left;" |''DMDrum'' | |||
{{SysCAD (Text, Help Link)}} | |||
|- | |||
! colspan="3" style="text-align:left;" |''Parameters'' | |||
|- style="vertical-align:top;" | |||
|MediumSolids | |||
|Input / List | |||
|Specifies which species should be considered as the medium solids by the model. | |||
* The drop down list will contain all solids species in the project, plus "-" for no selection. | |||
* See [[#Medium_solids|Medium solids]] for more information. | |||
|- style="vertical-align:top;" | |||
|MediumDensity / Rhom | |||
|style="background: #eaecf0" | Input / Display | |||
|Density of the medium. | |||
* User input value if ''MediumSolids'' is "-". | |||
* Set by the properties of the selected medium solids species in the feed otherwise. | |||
|- | |||
|MediumViscosity / mu | |||
|style="background: #eaecf0" | Input / Display | |||
|Viscosity of the medium. Automatically calculated if ''ViscosityModel'' is enabled. | |||
|- | |||
|ParticleShapeFactor / k | |||
|Input | |||
|Particle shape factor. | |||
|- | |||
|TerminalVelocity100 / V100 | |||
|Input | |||
|Terminal velocity of particles that are 100% recovered to sinks. | |||
|- | |||
|SizeCoefficient / A | |||
|Input | |||
|Coefficient of the size relation. | |||
|- | |||
|SizeConstant / B | |||
|Input | |||
|Constant term of the size relation. | |||
{{SysCAD (Text, Dense Medium, Liquids)|method=0}} | |||
|- | |||
! colspan="3" style="text-align:left;" |''Results'' | |||
|- | |||
|CutDensity / Rho50 | |||
|style="background: #eaecf0" | Display | |||
|Unsized cut density (Rho50). | |||
|- | |||
|EcartProbable / Ep | |||
|style="background: #eaecf0" | Display | |||
|Unsized Ecart Probable (Ep). | |||
|- | |||
|Imperfection / I | |||
|style="background: #eaecf0" | Display | |||
|Unsized partition Imperfection (I). | |||
|} | |||
{{SysCAD (Page, Hydrocyclone, Partition)|ActionU=Partition|ActionL=partition|DestinationU=Sinks|DestinationL=sinks|UnitL=dense medium separator|GravityMetrics=false|Rho50Ep=Display}} | |||
==== Viscosity page ==== | |||
This page displays the inputs and results for [[Properties (Dense Medium Viscosity)|dense medium viscosity]] calculations. The page is only visible if ''ViscosityModel'' is selected on the '''{{SysCAD (Text, UnitType Prefix)}}DenseMedium''' page. | |||
{{SysCAD (Page, About)}} | |||
{{SysCAD (Text, Dense Medium, Medium Solids)}} | |||
:* In addition, the ''MediumDensity'' parameter is set by the total medium solids plus liquids in the feed stream. | |||
==== Additional notes ==== | |||
{{SysCAD (Text, No PSD Splits)|gasstream=floats}} | |||
== | == External links == | ||
* [[ | * [https://help.syscad.net/Met_Dynamics_-_Dense_Medium_Separator Met Dynamics - Dense Medium Separator (help.syscad.net)] | ||
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Gravity,_Dense_Medium_and_Magnetic_Separation_Example Gravity, Dense Medium, and Magnetic Separation Example project (help.syscad.net)] | |||
== References == | == References == | ||
| Line 23: | Line 331: | ||
[[Category:Excel]] | [[Category:Excel]] | ||
[[Category:SysCAD]] | [[Category:SysCAD]] | ||
Latest revision as of 02:41, 27 June 2025
Description
This article describes the Baguley and Napier-Munn (1996) model for dense medium drums or bath-type separators.[1]
Model theory
Partition metrics
Several metrics are provided to characterise the partition curve.[2]
The , also known as the cut or separation density, is defined as the density of a particle of a given size which has an even (50%) chance of appearing in either the concentrate or tails stream.
The Ecart Probable, or , is a measure of the deviation of a partition curve from a perfect separation, and is typically defined for density separations as:
where and are the densities of particles which have a 75% and 25% probability, respectively, of appearing in the concentrate stream.
The Imperfection, , is a normalised measure of the sharpness of separation, which is suggested to be independent of the magnitude of the , and is typically defined for density separations as:
The and for each size interval and the overall mass are determined by fitting the model-calculated partitions to the logistic Rho-50-Ep equation.
Excel
The Baguley dense medium drum model may be invoked from the Excel formula bar with the following function call:
=mdUnit_DMDrum_Baguley(Parameters as Range, Size as Range, Density As Range, Feed as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:
where:
- is the number of size intervals
- is the number of density classes
- is the size of the square mesh interval that feed mass is retained on (mm)
- is feed solids mass flow rate by size and ore type (t/h)
- is the particle density (t/m3)
Results
The results are displayed in Excel as an array corresponding to the matrix notation below:
where:
- is mass flow rate of solids to the sinks stream (t/h)
- is mass flow rate of solids to the floats stream (t/h)
- is the actual partition of all mass to the sinks stream, computed as (frac)
- is the actual partition of all particles of size to the sinks stream, computed as (frac)
- is the actual partition of all particles of density class to the sinks stream, computed as (frac)
Example
The images below show the selection of input arrays and output results in the Excel interface.
SysCAD
MD_DenseMedium page
The first tab page in the access window will have this name.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Tag | Display | This name tag may be modified with the change tag option. |
| Condition | Display | OK if no errors/warnings, otherwise lists errors/warnings. |
| ConditionCount | Display | The current number of errors/warnings. If condition is OK, returns 0. |
| GeneralDescription / GenDesc | Display | This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.
If this field is blank, then SysCAD will display the unit class ID. |
| Requirements | ||
| On | CheckBox | This enables the unit. If this box is not checked, then the MassFracToSinks option appears below. |
| MassFracToSinks | Input | Only appears if the On field above is not checked. Specifies the fraction of feed mass that reports to the sinks stream when the model is off. |
| NumParallelUnits | Input | The number of parallel, identical units to simulate:
|
| Method | Partition (User) | The partition to sinks for each size interval and species is defined by the user. |
| Partition (Rho50-Ep) | The partition to sinks for each species and size interval is defined by the Rh050-Ep model. | |
| Partition (Pivot) | The partition to sinks for each species and size interval is defined by the Pivot model. | |
| Partition (Stochastic) | The partition to sinks for each species and size interval is defined by the Stochastic model. | |
| Drum (Baguley) | The Baguley dense medium drum model is used to determine the partition of solids to sinks and floats for each species and size interval. | |
| Cyclone (Dunglison) | The Dunglison dense medium cyclone model is used to determine the partition of solids to sinks (underflow) and floats (overflow) for each species and size interval. | |
| ViscosityModel | CheckBox | Show dense medium viscosity model on the Viscosity page. |
| Options | ||
| ShowQFeed | CheckBox | QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream. |
| ShowQSinks | CheckBox | QSinks and associated tab pages (eg Sp) will become visible, showing the properties of the sinks stream. |
| ShowQFloats | CheckBox | QFloats and associated tab pages (eg Sp) will become visible, showing the properties of the floats stream. |
| SizeForPassingFracCalc | Input | Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section. |
| FracForPassingSizeCalc | Input | Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section. |
| Stream Summary | ||
| MassFlow / Qm | Display | The total mass flow in each stream. |
| SolidMassFlow / SQm | Display | The Solids mass flow in each stream. |
| LiquidMassFlow / LQm | Display | The Liquid mass flow in each stream. |
| VolFlow / Qv | Display | The total Volume flow in each stream. |
| Temperature / T | Display | The Temperature of each stream. |
| Density / Rho | Display | The Density of each stream. |
| SolidFrac / Sf | Display | The Solid Fraction in each stream. |
| LiquidFrac / Lf | Display | The Liquid Fraction in each stream. |
| Passing | Display | The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream. |
| Passes | Display | The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction. |
Drum page
The Drum page is used to specify the required model method and associated input parameters.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| DMDrum | ||
| HelpLink | Opens a link to this page using the system default web browser. Note: Internet access is required. | |
| Parameters | ||
| MediumSolids | Input / List | Specifies which species should be considered as the medium solids by the model.
|
| MediumDensity / Rhom | Input / Display | Density of the medium.
|
| MediumViscosity / mu | Input / Display | Viscosity of the medium. Automatically calculated if ViscosityModel is enabled. |
| ParticleShapeFactor / k | Input | Particle shape factor. |
| TerminalVelocity100 / V100 | Input | Terminal velocity of particles that are 100% recovered to sinks. |
| SizeCoefficient / A | Input | Coefficient of the size relation. |
| SizeConstant / B | Input | Constant term of the size relation. |
| Liquids | ||
| LiquidsSeparMethod | Split To Sinks (User) | Liquids are split to sinks by a user-defined fraction of liquids in the feed. |
| Sinks Solids Fraction | Sufficient liquids mass is recovered to the sinks stream to yield the user-defined sinks solids mass fraction value (if possible). | |
| Sinks Liquids Fraction | Sufficient liquids mass is recovered to the sinks stream to yield the user-defined sinks liquids mass fraction value (if possible). | |
| SinksSolidsFracReqd / Sinks.SfReqd | Input | Required value of the mass fraction of solids in the sinks stream. Only visible if Sinks Solids Fraction is selected. |
| SinksLiquidsFracReqd / Sinks.LfReqd | Input | Required value of the mass fraction of liquids in the sinks stream. Only visible if Sinks Liquids Fraction is selected. |
| LiqSplitToSinks / Sinks.LiqSplit | Input/Display | The fraction of feed liquids recovered to the sinks stream. |
| Results | ||
| CutDensity / Rho50 | Display | Unsized cut density (Rho50). |
| EcartProbable / Ep | Display | Unsized Ecart Probable (Ep). |
| Imperfection / I | Display | Unsized partition Imperfection (I). |
Partition page
The Partition page is used to display (or specify) the partition by species/component/element/individual phase and size values.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| Distribution | ||
| Name | Display | Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream. |
| IntervalCount | Display | Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream. |
| SpWithPSDCount | Display | Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality. |
| Partition | ||
| Method | Model / User | Select model-calculated or user-defined partition to separate each solids species type. |
| Density | Display | Density of each solid species. |
| Size | Display | Size of each interval in mesh series. |
| MeanSize | Display | Geometric mean size of each interval in mesh series. |
| CutDensity / Rho50 | Display | Cut density (Rho50) of all particles in each size interval. |
| EcartProbable / Ep | Display | Ecart Probable (Ep) of all particles in each size interval. |
| All (All column) | Display |
|
| Partition | Display |
|
| All (All row, All column) | Display |
|
| All (All row, per species) | Display |
|
| CmpPartition | ||
| Components | Hides or shows component partition table. | |
| Size | Display | Size of each interval in mesh series. |
| MeanSize | Display | Geometric mean size of each interval in mesh series. |
| All (All column) | Display |
|
| CmpPartition | Display |
|
| All (All row, All column) | Display |
|
| All (All row, per component) | Display |
|
| ElePartition | ||
| Elements | Hides or shows element partition table. | |
| Size | Display | Size of each interval in mesh series. |
| MeanSize | Display | Geometric mean size of each interval in mesh series. |
| All (All column) | Display |
|
| ElePartition | Display |
|
| All (All row, All column) | Display |
|
| All (All row, per element) | Display |
|
| IPhPartition | ||
| IPhases | Hides or shows individual phases partition table. | |
| Size | Display | Size of each interval in mesh series. |
| MeanSize | Display | Geometric mean size of each interval in mesh series. |
| All (All column) | Display |
|
| IPhPartition | Display |
|
| All (All row, All column) | Display |
|
| All (All row, per individual phase) | Display |
|
Viscosity page
This page displays the inputs and results for dense medium viscosity calculations. The page is only visible if ViscosityModel is selected on the MD_DenseMedium page.
About page
This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| About | ||
| HelpLink | Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required. | |
| Information | Copies Product and License information to the Windows clipboard. | |
| Product | ||
| Name | Display | Met Dynamics software product name |
| Version | Display | Met Dynamics software product version number. |
| BuildDate | Display | Build date and time of the Met Dynamics Models SysCAD Add-On. |
| License | ||
| File | This is used to locate a Met Dynamics software license file. | |
| Location | Display | Type of Met Dynamics software license or file name and path of license file. |
| SiteCode | Display | Unique machine identifier for license authorisation. |
| ReqdAuth | Display | Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime. |
| Status | Display | License status, LICENSE_OK indicates a valid license, other messages report licensing errors. |
| IssuedTo | Display | Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to. |
| ExpiryDate | Display | Only visible if Met Dynamics license file is used. License expiry date. |
| DaysLeft | Display | Only visible if Met Dynamics license file is used. Days left before the license expires. |
Medium solids
This model allows the user to designate any single SysCAD solids species in the project as the medium solids. Alternatively, no medium solids may be specified (default: "-").
The selected option determines how the medium species is treated by the model:
- Default: -:
- All solids species in the feed stream that possess the size distribution (PSD) property are partitioned by the model based on their size and density characteristics.
- The All partition values shown on the Partition page include contributions from all species.
- All solids species in the feed stream that do not possess the PSD property are split by the model based on default behaviour (see Additional notes).
- [Species Name]:
- The user may specify how the selected medium solids species is split to the sinks stream via the MedSolSeparMethod field. Options are:
- None: Medium solids are split as if the default MediumSolids parameter "-" was selected. See above.
- Split to Sinks (User): The user specifies the fractional split of the selected medium solids species to the sinks stream.
- Follow Solids: The fractional split of the selected medium solids species to the sinks stream is equal to the overall mass split of all other solids to the sinks stream.
- Follow Liquids: The fractional split of the selected medium solids species to the sinks stream is equal to the mass split of liquids to the sinks stream.
- if the selected medium solids species posseses the PSD property:
- The partition-by-size values for the medium species on the Partition page are displayed as zeroes.
- The All partition values on the Partition page exclude the medium solids species.
- In addition, the MediumDensity parameter is set by the total medium solids plus liquids in the feed stream.
- The user may specify how the selected medium solids species is split to the sinks stream via the MedSolSeparMethod field. Options are:
Additional notes
- Solid species that do not possess a particle size distribution property are split according to the overall mass split of the default particle size distribution species selected in the SysCAD Project Configuration.
- If the default particle size distribution species is not present in the unit feed, the overall split of all other species with particle size distributions combined is used, as determined by the model.
- Gas phase species report directly to the floats stream without split.
External links
- Met Dynamics - Dense Medium Separator (help.syscad.net)
- Gravity, Dense Medium, and Magnetic Separation Example project (help.syscad.net)
References
- ↑ Baguley, P.J. and Napier-Munn, T.J., 1996. A mathematical model of the dense medium drum. Transactions of the Institute of Mining and Metallurgy Section C Mineral Processing and Extractive Metallurgy, 105(Jan-April), pp.C1-C8.
- ↑ Gupta, A. and Yan, D.S., 2016. Mineral processing design and operations: an introduction. Elsevier.