Partition (Size, Bazin): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
imported>Scott.Munro
 
imported>Scott.Munro
 
(One intermediate revision by the same user not shown)
Line 3: Line 3:
This article describes the Bazin et al. (2014) empirical expression for the recovery of particles to the concentrate stream of a spiral concentrator.{{Bazin et al. (2014)}}
This article describes the Bazin et al. (2014) empirical expression for the recovery of particles to the concentrate stream of a spiral concentrator.{{Bazin et al. (2014)}}


The form of the empirical equation may also be applicable to the Falcon gravity concentrator in some circumstances, as observed by Dehaine et al (2016).{{Dehaine et al (2016)}}
The form of the empirical equation may also be applicable to other gravity concentration processes exhibiting a similar reverse classification effect on coarser particles, such as shaking tables and the Falcon gravity concentrator.{{Bergmann et al. (2016)}}{{Dehaine et al (2016)}}


== Model theory ==
== Model theory ==


[[File:PartitionBazin1.png|thumb|450px|Figure 1. Bazin partitions to concentrate, for three minerals with differing densities.]]
[[File:PartitionBazin1.png|thumb|450px|Figure 1. Bazin partitions to concentrate for three minerals with differing densities (after Bazin et al. (2014).{{Bazin et al. (2014)}}]]


Bazin et al. (2014) proposed an empirical expression for the partition of particles of a given size and density to the concentrate stream of a spiral concentrator. The concentrate stream is defined here as the inner part of the spiral trough.
Bazin et al. (2014) proposed an empirical expression for the partition of particles of a given size and density to the concentrate stream of a spiral concentrator. The concentrate stream is defined here as the inner part of the spiral trough.
Line 27: Line 27:


:<math>P_{\rm R}(d_i, \rho_j) = R_{\rm P}(\rho_j) + (1 - R_{\rm P}(\rho_j))\left \{ 1 - \left [ \dfrac{\exp \left( \alpha_{\rm P}(\rho_j) \dfrac{\bar d_i}{d_{50;\rm P}(\rho_j)}\right ) - 1}{\exp \left( \alpha_{\rm P}(\rho_j) \dfrac{\bar d_i}{d_{50;\rm P}(\rho_j)}\right ) + \exp \big( \alpha_{\rm P}(\rho_j)\big) - 2} \right ] \right \}</math>
:<math>P_{\rm R}(d_i, \rho_j) = R_{\rm P}(\rho_j) + (1 - R_{\rm P}(\rho_j))\left \{ 1 - \left [ \dfrac{\exp \left( \alpha_{\rm P}(\rho_j) \dfrac{\bar d_i}{d_{50;\rm P}(\rho_j)}\right ) - 1}{\exp \left( \alpha_{\rm P}(\rho_j) \dfrac{\bar d_i}{d_{50;\rm P}(\rho_j)}\right ) + \exp \big( \alpha_{\rm P}(\rho_j)\big) - 2} \right ] \right \}</math>
:<math>Y_{ij} = S_{\rm c}(d_i, \rho_j) \times P_{\rm R}(d_i, \rho_j)</math>


where:
where:
Line 32: Line 34:
* <math>j</math> is the index of the density class, <math>j = \{1,2,\dots,m\}</math>, <math>m</math> is the number of density classes
* <math>j</math> is the index of the density class, <math>j = \{1,2,\dots,m\}</math>, <math>m</math> is the number of density classes
* <math>\bar d_{i}</math> is the [[Conversions|geometric mean size]] of particles in size interval <math>i</math> (mm)
* <math>\bar d_{i}</math> is the [[Conversions|geometric mean size]] of particles in size interval <math>i</math> (mm)
* <math>\alpha_{\rm S}(\rho)</math> is the sharpness parameter of the classification curve
* <math>\alpha_{\rm S}(\rho_j)</math> is the sharpness parameter of the classification curve
* <math>d_{\rm 50;S}(\rho)</math> is the size of a particle of density <math>d\rho</math> which has a 50% probability of reporting to the concentrate stream (mm)
* <math>d_{\rm 50;S}(\rho_j)</math> is the size of a particle of density <math>\rho_j</math> which has a 50% probability of reporting to the concentrate stream (mm)
* <math>R_{\rm P}</math> is the fraction of fine particles which are entrained by the classification action towards the inner section of the spiral trough (frac)
* <math>R_{\rm P}(\rho_j)</math> is the fraction of fine particles of density <math>\rho_j</math> which are entrained by the classification action towards the inner section of the spiral trough (frac)
* <math>\alpha_{\rm P}(\rho)</math> is the sharpness parameter of the filtration curve
* <math>\alpha_{\rm P}(\rho_j)</math> is the sharpness parameter of the filtration curve
* <math>d_{\rm 50;P}(\rho)</math> is the size of a particle of density <math>d\rho</math> for which 50% are rejected for classification by the Bagnold force (mm)
* <math>d_{\rm 50;P}(\rho_j)</math> is the size of a particle of density <math>\rho_j</math> for which 50% are rejected for classification by the Bagnold (or other counteracting) force (mm)
* <math>Y_{ij}</math> is the fraction of the mass of particles in size class <math>i</math> and density class <math>j</math> which are partitioned (recovered) to the concentrate stream (frac)


A separate set of <math>\alpha_{\rm S}</math>, <math>d_{\rm 50;S}</math>, <math>R_{\rm P}</math>, <math>\alpha_{\rm P}</math>, and <math>d_{\rm 50;P}</math> parameters are required for each particle with a distinct density (e.g. mineral species).
A separate set of <math>\alpha_{\rm S}</math>, <math>d_{\rm 50;S}</math>, <math>R_{\rm P}</math>, <math>\alpha_{\rm P}</math>, and <math>d_{\rm 50;P}</math> parameters are required for each particle with a distinct density (e.g. mineral species).
{{Model theory (Text, Gravity Concentrator, Middlings)}}


== Excel ==
== Excel ==
Line 62: Line 67:
\end{bmatrix}\\
\end{bmatrix}\\
\\
\\
alphaS & = \big [\alpha_S(\rho) \big ]\\
alphaS & = \big [\alpha_S(\rho_j) \big ]\\
d50S & = \big [d_{50; \rm S}(\rho) \text{ (mm)}\big ]\\
d50S & = \big [d_{50; \rm S}(\rho_j) \text{ (mm)}\big ]\\
Rp & = \big [R_{\rm p}(\rho)\text{ (frac)}\big ]\\
Rp & = \big [R_{\rm p}(\rho_j)\text{ (frac)}\big ]\\
alphaP & = \big [\alpha_P(\rho) \big ]\\
alphaP & = \big [\alpha_P(\rho_j) \big ]\\
d50P & = \big [d_{50; \rm P}(\rho) \text{ (mm)}\big ]\\
d50P & = \big [d_{50; \rm P}(\rho_j) \text{ (mm)}\big ]\\
\end{align}</math>
\end{align}</math>
|
|
Line 72: Line 77:
mdPartition\_Bazin =  
mdPartition\_Bazin =  
\begin{bmatrix}
\begin{bmatrix}
(y(d_1, \rho)\text{ (frac)}
Y_{1j}\text{ (frac)}
\\
\\
\vdots
\vdots
\\
\\
(y(d_n, \rho)\text{ (frac}
Y_{nj}\text{ (frac)}
\\
\\
\end{bmatrix}
\end{bmatrix}
Line 90: Line 95:


The sections and variable names used in the SysCAD interface are described in detail in the following tables.
The sections and variable names used in the SysCAD interface are described in detail in the following tables.
Note that a '''Con''' and '''Partition''' page is provided provided for each connected concentrate discharge stream of a Gravity Concentrator unit model.


{{SysCAD (Page, Gravity Concentrator, DLL*GravityConcentrator)}}
{{SysCAD (Page, Gravity Concentrator, DLL*GravityConcentrator)}}


==== Bazin page ====
==== Con page ====


The Bazin page is used to specify the input parameters for the Bazin model.
The Con page is used to specify the required model method and associated input parameters.


{{SysCAD (Text, Table Header)}}
{{SysCAD (Text, Table Header)}}


|-
{{SysCAD (Text, Gravity Concentrator, Con)}}
! colspan="3" style="text-align:left;" |''Bazin''


{{SysCAD (Text, Help Link)}}
{{SysCAD (Text, Help Link)}}


|-
! colspan="3" style="text-align:left;" |''Bazin''
|- style="vertical-align:top;"
|- style="vertical-align:top;"
|OreSpecific
|OreSpecific
Line 138: Line 146:
|}
|}


{{SysCAD (Page, Hydrocyclone, Partition)|ActionU=Partition|ActionL=partition|DestinationU=Concentrate|DestinationL=concentrate|UnitL=gravity concentrator|GravityMetrics=false}}
{{SysCAD (Page, Hydrocyclone, Partition)|ActionU=Partition|ActionL=partition|DestinationU=Concentrate|DestinationL=concentrate|UnitL=gravity concentrator|GravityMetrics=false|Cumulative=true}}


{{SysCAD (Page, About)}}
{{SysCAD (Page, About)}}
==== Additional notes ====
{{SysCAD (Text, No PSD Splits)|gasstream=tail}}


== References ==
== References ==

Latest revision as of 15:28, 17 May 2024

Description

This article describes the Bazin et al. (2014) empirical expression for the recovery of particles to the concentrate stream of a spiral concentrator.[1]

The form of the empirical equation may also be applicable to other gravity concentration processes exhibiting a similar reverse classification effect on coarser particles, such as shaking tables and the Falcon gravity concentrator.[2][3]

Model theory

Figure 1. Bazin partitions to concentrate for three minerals with differing densities (after Bazin et al. (2014).[1]

Bazin et al. (2014) proposed an empirical expression for the partition of particles of a given size and density to the concentrate stream of a spiral concentrator. The concentrate stream is defined here as the inner part of the spiral trough.

The expression is formulated as the product of two counter-acting mechanisms that simultaneously force heavy minerals to the centre of the trough and coarse particles to the outer edge of the trough.

The partition of particles of a given size and density to the concentrate stream, (frac), is:

where:

  • is the fraction of particles which should nominally report to the inner part of the trough (concentrate stream) due to gravitational forces, the classification action
  • is the probability that a particle resists the inward forces and is directed towards the outer trough by the Bagnold force, the filtration action
  • and are the diameter (mm) and density (t/m3) of the particle respectively

For series of size intervals, the and terms are computed as:

where:

  • is the index of the size interval, , is the number of size intervals
  • is the index of the density class, , is the number of density classes
  • is the geometric mean size of particles in size interval (mm)
  • is the sharpness parameter of the classification curve
  • is the size of a particle of density which has a 50% probability of reporting to the concentrate stream (mm)
  • is the fraction of fine particles of density which are entrained by the classification action towards the inner section of the spiral trough (frac)
  • is the sharpness parameter of the filtration curve
  • is the size of a particle of density for which 50% are rejected for classification by the Bagnold (or other counteracting) force (mm)
  • is the fraction of the mass of particles in size class and density class which are partitioned (recovered) to the concentrate stream (frac)

A separate set of , , , , and parameters are required for each particle with a distinct density (e.g. mineral species).

Middlings

Gravity concentrators such as jigs, spirals and shaking tables produce a bed or band of partially stratified components at the point of discharge. Portions of the bed or band are then typically directed to product streams by a physical device, such as a weir, 'splitter' or 'cutter'. These devices are usually adjustable, and can be arranged to recover arbitrary fractions of the bed or band.

From a physical standpoint, adjusting the discharge device to recover more of the bed or band has the effect of recovering the both the portion from the previous position plus the portion in between the previous and new positions. As more mass is recovered by this process, the partition curve effectively 'shifts upwards'. The partition curve is thus representing the cumulative recovery of mass from all positions between the beginning of the bed/band and the discharge device position.

Mathematically, the partition curve generated by such a gravity concentration method should also be considered a cumulative recovery of mass to concentrate. When multiple product streams exist, e.g. concentrate and middlings, the partition of components to each individual product stream will be the difference between the cumulative partition curves at each product stream position.[4] That is,

where:

  • is the index of the product stream, i.e. is the first concentrate stream, are subsequent lower-grade concentrate or middlings streams
  • is the mass fraction of particles in the feed stream in size class and density class which are partitioned to the product stream (frac)
  • is the cumulative mass fraction of particles in the feed stream in size class and density class which are partitioned to all the products streams up to and including (frac)
  • The term prevents negative partition values

The cumulative recovery formulation described above is physically and mathematically distinct from staged recovery processes which apply partition curves to the unrecovered streams of previous partition steps.

Excel

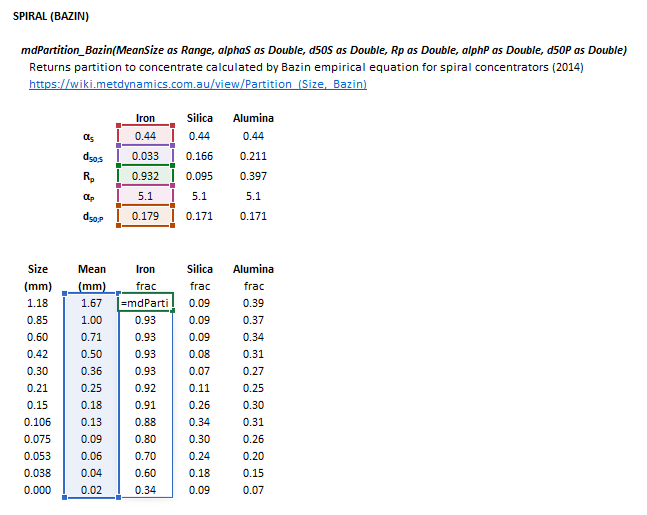
The Bazin spiral partition model may be invoked from the Excel formula bar with the following function call: 

=mdPartition_Bazin(MeanSize as Range, alphaS as Double, d50S as Double, Rp as Double, alphP as Double, d50P as Double)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The input parameters and model results are defined below in matrix notation, along with an example image showing the selection of the same cells in the Excel interface:

Figure 2. Example showing the selection of the input parameters (shaded cells), and Results (light blue frame) array in Excel.

SysCAD

The Bazin partition is available from the MetDynamics*GravityConcentrator unit model.

The sections and variable names used in the SysCAD interface are described in detail in the following tables.

Note that a Con and Partition page is provided provided for each connected concentrate discharge stream of a Gravity Concentrator unit model.

MD_GravityConcentrator page

The first tab page in the access window will have this name.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Tag Display This name tag may be modified with the change tag option.
Condition Display OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount Display The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc Display This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.

If this field is blank, then SysCAD will display the unit class ID.

Requirements
On CheckBox This enables the unit. If this box is not checked, then the MassFracToCon option appears below.
MassFracToCon Input Only appears if the On field above is not checked. Specifies the fraction of feed mass that reports to the concentrate stream when the model is off.
Options
ShowQFeed CheckBox QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream.
SizeForPassingFracCalc Input Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section.
FracForPassingSizeCalc Input Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section.
Stream Summary
MassFlow / Qm Display The total mass flow in each stream.
SolidMassFlow / SQm Display The Solids mass flow in each stream.
LiquidMassFlow / LQm Display The Liquid mass flow in each stream.
VolFlow / Qv Display The total Volume flow in each stream.
Temperature / T Display The Temperature of each stream.
Density / Rho Display The Density of each stream.
SolidFrac / Sf Display The Solid Fraction in each stream.
LiquidFrac / Lf Display The Liquid Fraction in each stream.
Passing Display The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream.
Passes Display The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction.

Con page

The Con page is used to specify the required model method and associated input parameters.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Stage
On Checkbox This enables the stage. If off, the feed to this stage passes directly to the next stage (or tail) without partition.
Method Partition (User) The partition to concentrate for each size interval is defined by the user.
Partition (Pivot) The partition to concentrate for each size interval is defined by the Pivot model.
Partition (Stochastic) The partition to concentrate for each size interval is defined by the Stochastic model.
Partition (Bazin) The partition to concentrate for each size interval is defined by the Bazin model.
Jig (King) The partition to concentrate for each size interval is defined by the King jig stratification model.
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
Bazin
OreSpecific CheckBox
  • Ore-specific partitions, allows the Bazin equation parameters to be separately input for all species.
  • Default is all species have a separate set of input properties.
  • This option is only available if there is more than one species in the project with the size distribution property.
Parameters
AlphaS Input The Bazin equation alphaS parameter for the classification curve.
d50S Input The Bazin equation d50S cut size parameter for the classification curve.
Rp Input The Bazin equation Rp parameter for the filtration curve.
AlphaP Input The Bazin equation alphaP parameter for the filtration curve.
d50P Input The Bazin equation d50P cut size parameter for the filtration curve.
Liquids
LiquidsSeparMethod Split To Con (User) Liquids are split to concentrate by a user-defined fraction of liquids in the feed.
Con Solids Fraction Sufficient liquids mass is recovered to the concentrate stream to yield the user-defined concentrate solids mass fraction value (if possible).
Con Liquids Fraction Sufficient liquids mass is recovered to the concentrate stream to yield the user-defined concentrate liquids mass fraction value (if possible).
ConSolidsFracReqd / Con.SfReqd Input Required value of the mass fraction of solids in the concentrate stream. Only visible if Con Solids Fraction is selected.
ConLiquidsFracReqd / Con.LfReqd Input Required value of the mass fraction of liquids in the concentrate stream. Only visible if Con Liquids Fraction is selected.
LiqSplitToCon / Con.LiqSplit Input/Display The fraction of feed liquids recovered to the concentrate stream.

Partition page

The Partition page is used to specify or display the partition by species and size values.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Distribution
Name Display Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream.
IntervalCount Display Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream.
SpWithPSDCount Display Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality.

CumulativePartition
Method Model/User Select model-calculated or user-defined cumulative partition to separate each solids species type.
Density Display Density of each solid species.
Size Display Size of each interval in mesh series.
MeanSize Display Geometric mean size of each interval in mesh series.
All (All column) Display
  • Actual overall cumulative partition to concentrates of all solid species, for each size interval.
  • Excludes solid species not present in the gravity concentrator feed.
CumulativePartition Display
  • Cumulative partition to concentrates for each size interval, in each solid species, as determined by the selected model or user defined value.
  • Note: These values are displayed regardless of whether the solid species is present in the gravity concentrator feed or not.
All (All row, All column) Display
  • Displays the actual, total, cumulative partition of all solids with a particle size distribution property in the feed to concentrates.
  • Excludes solid species not present in the gravity concentrator feed.
All (All row, per species) Display
  • Actual overall cumulative partition to concentrates for each solid species, for all size intervals in that species.
  • Excludes solid species not present in the gravity concentrator feed.
Partition
Method Model/User Select model-calculated or user-defined partition to separate each solids species type.
Density Display Density of each solid species.
Size Display Size of each interval in mesh series.
MeanSize Display Geometric mean size of each interval in mesh series.
All (All column) Display
  • Actual overall partition to concentrate of all solid species, for each size interval.
  • Excludes solid species not present in the gravity concentrator feed.
Partition Display
  • Partition to concentrate for each size interval, in each solid species, as determined by the selected model or user defined value.
  • Note: These values are displayed regardless of whether the solid species is present in the gravity concentrator feed or not.
All (All row, All column) Display
  • Displays the actual, total, partition of all solids with a particle size distribution property in the feed to concentrate.
  • Excludes solid species not present in the gravity concentrator feed.
All (All row, per species) Display
  • Actual overall partition to concentrate for each solid species, for all size intervals in that species.
  • Excludes solid species not present in the gravity concentrator feed.

About page

This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
About
HelpLink ButtonLicensingHelp.png Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required.
Information ButtonCopyToClipboard.png Copies Product and License information to the Windows clipboard.
Product
Name Display Met Dynamics software product name
Version Display Met Dynamics software product version number.
BuildDate Display Build date and time of the Met Dynamics Models SysCAD Add-On.
License
File ButtonBrowse.png This is used to locate a Met Dynamics software license file.
Location Display Type of Met Dynamics software license or file name and path of license file.
SiteCode Display Unique machine identifier for license authorisation.
ReqdAuth Display Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime.
Status Display License status, LICENSE_OK indicates a valid license, other messages report licensing errors.
IssuedTo Display Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to.
ExpiryDate Display Only visible if Met Dynamics license file is used. License expiry date.
DaysLeft Display Only visible if Met Dynamics license file is used. Days left before the license expires.

Additional notes

  • Solid species that do not possess a particle size distribution property are split according to the overall mass split of the default particle size distribution species selected in the SysCAD Project Configuration.
  • If the default particle size distribution species is not present in the unit feed, the overall split of all other species with particle size distributions combined is used, as determined by the model.
  • Gas phase species report directly to the tail stream without split.

References

  1. ↑ 1.0 1.1 Bazin, C., Sadeghi, M., Roy, P., Bourassa, M., Cataford, D., Lavoie, F., Rochefort, C., Gosselin, C., Renaud, M. and Mahieu, G., 2014. Simulation of an iron ore concentration circuit using mineral size recovery curves of industrial spirals. Proceedings of the 46th Canadian Mineral Processors, CIM, Ottawa, Canada, January, pp.21-23.
  2. ↑ Bergmann, C., Govender, V. and Corfield, A.A., 2016. Using mineralogical characterisation and process modelling to simulate the gravity recovery of ferrochrome fines. Minerals Engineering, 91, pp.2-15.
  3. ↑ Dehaine, Q., Foucaud, Y., Kroll-Rabotin, J.S. and Filippov, L.O., 2019. Experimental investigation into the kinetics of Falcon UF concentration: Implications for fluid dynamic-based modelling. Separation and Purification Technology, 215, pp.590-601.
  4. ↑ King, R.P., Juckes, A.H. and Stirling, P.A., 1992. A quantitative model for the prediction of fine coal cleaning in a spiral concentrator. Coal preparation, 11(1-2), pp.51-66.
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Partition_(Size,_Bazin)&oldid=2008"