Pump (Centrifugal, Slurry): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
md>Scott.Munro
imported>Scott.Munro
 
(9 intermediate revisions by 2 users not shown)
Line 15: Line 15:
== Model theory ==
== Model theory ==


{{Restricted content}}
<hide>
[[File:Pump1.png|450px|thumb|Figure 1. A pump characteristic curve in the format typically provided by vendors, after Weir (2009).{{Weir (2009)}}]]
[[File:Pump1.png|450px|thumb|Figure 1. A pump characteristic curve in the format typically provided by vendors, after Weir (2009).{{Weir (2009)}}]]


Line 27: Line 30:
* The transport medium is water between 0 and 60 °C
* The transport medium is water between 0 and 60 °C


</hide><div class="user-show">
=== Generalised characteristic curves ===
=== Generalised characteristic curves ===
</div><hide>


The performance of a centrifugal pump is typically described by a set of ''characteristic'' curves relating pressure head, flow rate, pump speed and efficiency, as illustrated by the example in Figure 1.
The performance of a centrifugal pump is typically described by a set of ''characteristic'' curves relating pressure head, flow rate, pump speed and efficiency, as illustrated by the example in Figure 1.
Line 33: Line 38:
King (2002) describes a method for generalising the multiple characteristic curves into a reduced functional form.{{King (2002)}}
King (2002) describes a method for generalising the multiple characteristic curves into a reduced functional form.{{King (2002)}}


==== Speed ====  
</hide><div class="user-show">
==== Speed ====
</div><hide>


King's procedure begins by specifying the pump head and flow rate in terms of two dimensionless groups, the pump head number, <math>N_{\rm pu}</math>, and the pump flow number, <math>N_{\rm Q}</math>,:
King's procedure begins by specifying the pump head and flow rate in terms of two dimensionless groups, the pump head number, <math>N_{\rm pu}</math>, and the pump flow number, <math>N_{\rm Q}</math>,:
Line 60: Line 67:
The volumetric '''flow rate''' provided by a pump operating at a given speed and pressure head can be computed via the quadratic formula:
The volumetric '''flow rate''' provided by a pump operating at a given speed and pressure head can be computed via the quadratic formula:


:<math> N_{\rm Q} = \dfrac{- B_{\rm N} - \sqrt{{B_{\rm N}}^2 + 4 C_{\rm N} (A_{\rm N} - N_{\rm pu})}}{2 C_{\rm N}}</math>
:<math> N_{\rm Q} = \dfrac{B_{\rm N} - \sqrt{{B_{\rm N}}^2 + 4 C_{\rm N} (A_{\rm N} - N_{\rm pu})}}{-2 C_{\rm N}}</math>


and <math>Q = N_{\rm Q} \cdot N \cdot {D_{\rm imp}}^3</math>.
and <math>Q = N_{\rm Q} \cdot N \cdot {D_{\rm imp}}^3</math>.
Line 68: Line 75:
:<math>\dfrac{H_{\rm t} g}{N^2{D_{\rm imp}}^2} = A_{\rm N} - B_{\rm N} \left (\dfrac{Q}{N \cdot {D_{\rm imp}}^3} \right ) - C_{\rm N} \left( \dfrac{Q}{N \cdot {D_{\rm imp}}^3} \right)^2 \implies N = \dfrac{B_{\rm N} Q + \sqrt{(B_{\rm N}Q)^2 - 4 A_{\rm N} (-g{D_{\rm imp}}^4H_{\rm t}-C_{\rm N}Q^2)}}{2 {D_{\rm imp}}^3 A_{\rm N}}</math>
:<math>\dfrac{H_{\rm t} g}{N^2{D_{\rm imp}}^2} = A_{\rm N} - B_{\rm N} \left (\dfrac{Q}{N \cdot {D_{\rm imp}}^3} \right ) - C_{\rm N} \left( \dfrac{Q}{N \cdot {D_{\rm imp}}^3} \right)^2 \implies N = \dfrac{B_{\rm N} Q + \sqrt{(B_{\rm N}Q)^2 - 4 A_{\rm N} (-g{D_{\rm imp}}^4H_{\rm t}-C_{\rm N}Q^2)}}{2 {D_{\rm imp}}^3 A_{\rm N}}</math>


</hide><div class="user-show">
==== Efficiency ====
==== Efficiency ====
</div><hide>


Although not explicitly described by King, the efficiency characteristic curves are also amenable to the same generalisation procedure as the speed curves, i.e.:
Although not explicitly described by King, the efficiency characteristic curves are also amenable to the same generalisation procedure as the speed curves, i.e.:
Line 78: Line 87:
As with the speed curves, regression techniques may be applied to extract the coefficients of the above equation, an example of which is shown in the lower part of Figure 2.
As with the speed curves, regression techniques may be applied to extract the coefficients of the above equation, an example of which is shown in the lower part of Figure 2.


</hide><div class="user-show">
=== Total dynamic head ===
=== Total dynamic head ===
</div><hide>


The ''total dynamic head'' is the equivalent pressure head that a pump acts against, taking into account static head, friction losses in the pipe, and pressure drops across connected equipment at the piping terminus, i.e.:
The ''total dynamic head'' is the equivalent pressure head that a pump acts against, taking into account static head, friction losses in the pipe, and pressure drops across connected equipment at the piping terminus, i.e.:
Line 108: Line 119:
* Iterative solution is not required when pump speed is being computed at a fixed feed flow rate.
* Iterative solution is not required when pump speed is being computed at a fixed feed flow rate.


</hide><div class="user-show">
==== Friction factor ====
==== Friction factor ====
</div><hide>


Many methods exist to estimate the friction factor, <math>f</math>, e.g. see [https://en.wikipedia.org/wiki/Darcy_friction_factor_formulae here].
Many methods exist to estimate the friction factor, <math>f</math>, e.g. see [https://en.wikipedia.org/wiki/Darcy_friction_factor_formulae here].
Line 124: Line 137:
where <math>\rho_{\rm SL}</math> is the density of slurry (t/m<sup>3</sup>) and <math>\mu</math> is the dynamic viscosity of the liquid (cP).  
where <math>\rho_{\rm SL}</math> is the density of slurry (t/m<sup>3</sup>) and <math>\mu</math> is the dynamic viscosity of the liquid (cP).  


The Colebrook equation is valid for Reynolds numbers in excess of 4,000. Furthermore, the Colebrook equation requires solution by iterative numerical means due to <math>f</math> appearing in both side of the equation.
The Colebrook equation is valid for Reynolds numbers in excess of 4,000. Furthermore, the Colebrook equation requires solution by iterative numerical means due to <math>f</math> appearing in both sides of the equation.


The '''Churchill''' approximation to Colebrook's formula is:
The '''Churchill''' approximation to Colebrook's formula is:
Line 138: Line 151:
The Churchill approximation accounts for flow in the laminar regime, from Reynolds numbers above about 10<sup>3</sup>, which is lower than the Colebrook equation.
The Churchill approximation accounts for flow in the laminar regime, from Reynolds numbers above about 10<sup>3</sup>, which is lower than the Colebrook equation.


</hide><div class="user-show">
=== Head ratio ===
=== Head ratio ===
</div><hide>


Pump characteristic curves, such that illustrated in Figure 1., are almost exclusively derived from testing on pure water.
Pump characteristic curves, such that illustrated in Figure 1., are almost exclusively derived from testing on pure water.
Line 146: Line 161:
Centrifugal slurry pump derating is undertaken by approximating the head of water that is equivalent to the head of a particular slurry being pumped, via the equation:
Centrifugal slurry pump derating is undertaken by approximating the head of water that is equivalent to the head of a particular slurry being pumped, via the equation:


:<math>H_{\rm w} = \dfrac{H_{\rm t}}{\mathit{HR}}</math>
:<math>H_{\rm w} = \dfrac{H_{\rm t}}{{\rm HR}}</math>


where <math>H_{\rm w}</math> is the equivalent head of water (m) and <math>\mathit{HR}</math> is the head ratio (m/m) for the slurry.  
where <math>H_{\rm w}</math> is the equivalent head of water (m) and <math>{\rm HR}</math> is the head ratio (m/m) for the slurry.  


The equivalent water head, <math>H_{\rm w}</math>, is then used in the characteristic curve equations above in place of the total head, <math>H_{\rm t}</math>.
The equivalent water head, <math>H_{\rm w}</math>, is then used in the characteristic curve equations above in place of the total head, <math>H_{\rm t}</math>.


The head ratio, <math>\mathit{HR}</math> can be estimated by many means. Two approaches are included in the centrifugal slurry pump model, the ''Cave'' and ''Warman'' approaches.
The head ratio, <math>{\rm HR}</math> can be estimated by many means. Two approaches are included in the centrifugal slurry pump model, the ''Cave'' and ''Warman'' approaches.


</hide><div class="user-show">
==== Cave method ====
==== Cave method ====
</div><hide>


The Cave equation is:{{Engin and Gur (2003)}}
The Cave equation is:{{Engin and Gur (2003)}}


:<math>\mathit{HR} = 1 - 0.0385 (\rho_{\rm S} - 1) \left ( \dfrac{\rho_{\rm S} + 4}{\rho_{\rm S}} \right ) C_{\rm W} \ln \left ( \dfrac{d_{50}}{22.7} \right )</math>
:<math>{\rm HR} = 1 - 0.0385 (\rho_{\rm S} - 1) \left ( \dfrac{\rho_{\rm S} + 4}{\rho_{\rm S}} \right ) C_{\rm W} \ln \left ( \dfrac{d_{50}}{22.7} \right )</math>


where:
where:
Line 165: Line 182:
* <math>\rho_{\rm S}</math> is the Specific Gravity or density of solids (- or t/m<sup>3</sup>)
* <math>\rho_{\rm S}</math> is the Specific Gravity or density of solids (- or t/m<sup>3</sup>)


</hide><div class="user-show">
==== Warman method ====
==== Warman method ====
</div><hide>


[[File:Pump3.png|x600px|thumb|link={{filepath:Pump3.png}}|Figure 3. Weir Head and Efficiency Ratios nomograph, after Grizina et al. (2002).{{Grzina et al. (2002)}} Example progression through the nomograph is indicated by dashed arrows. (Click image for larger view).]]
[[File:Pump3.png|x500px|thumb|link={{filepath:Pump3.png}}|Figure 3. Warman Head and Efficiency Ratios nomograph, after Grizina et al. (2002).{{Grzina et al. (2002)}} Example progression through the nomograph is indicated by dashed arrows. (Click image for larger view).]]


Warman provides a ''nomograph'' method for approximating the head ratio of a pumped slurry.{{Grzina et al. (2002)}} The nomograph form is reproduced in Figure 3, including an example path through the approximation procedure. The property <math>C_{\rm V}</math> used by the nomograph is the concentration of solids by volume in the slurry (v/v).
Warman provides a ''nomograph'' method for approximating the head ratio of a pumped slurry.{{Grzina et al. (2002)}} The nomograph form is reproduced in Figure 3, including an example path through the approximation procedure. The property <math>C_{\rm V}</math> used by the nomograph is the concentration of solids by volume in the slurry (v/v).


The Warman nomograph has been digitised and an interpolative calculation procedure is integrated into the centrifugal slurry pump model as an option for estimating the head ratio.
The Warman nomograph has been digitised and an interpolative calculation procedure is integrated into the centrifugal slurry pump model as an option for estimating the head ratio.
</hide><div class="user-show">
==== Weir / HI method ====
</div><hide>
Weir Minerals provide an updated method to estimate the head ratio based on the following equations:{{Roudnev and Loderer (2023)}}
:<math>\mathrm{HR} = 1 - 0.01 \cdot \left [ A \cdot \left ( \dfrac{1.11}{D_{\rm imp}} \right )^{0.9} \cdot {d_{50}}^B \cdot \left ( \dfrac{\rho_{\rm S} - \rho_{\rm L}}{1.65} \right )^{0.65} \cdot \dfrac{C_{\rm V}}{0.15} \cdot (1 - {C_{\rm fp}})^2 \right ]</math>
where:
:<math>A =
\begin{cases}
4.04, & D_{\rm imp} \leq 0.41 \text{ m}\\
0.005124 \, D_{\rm imp} + 1.9388, & 0.41 \text{ m} < D_{\rm imp} \leq 0.90 \text{ m}\\
6.5, & D_{\rm imp} > 0.89 \text{ m}\\
\end{cases}
</math>
:<math>B = 0.4 \cdot \left ( d_{50} \right )^{-0.25}</math>
and:
* <math>C_{\rm V}</math> is the concentration of solids in the slurry by volume (v/v)
* <math>C_{\rm fp}</math> is cumulative fraction passing 75 μm of particles in the feed (frac)
* <math>\rho_{\rm L}</math> is the density of liquids (t/m<sup>3</sup>)
Weir Minerals refer to this approach as the ''Weir Standard''. The method appears to be functionally equivalent to the Hydraulic Institute (HI) method described in ''ANSI/HI 12.1-12.6-2016 Rotodynamic Centrifugal Slurry Pumps''.{{Hydraulic Institute (2016)}}
</hide><div class="user-show">


=== Efficiency ratio ===
=== Efficiency ratio ===
</div><hide>


Similarly to the head ratio, the efficiency ratio <math>\mathit{ER}</math> (kW/kW) derates pump efficiency for slurry duty, i.e.:
Similarly to the head ratio, the efficiency ratio <math>{\rm ER}</math> (kW/kW) derates pump efficiency for slurry duty, i.e.:


:<math>E_{\mathit{eff}} = \mathit{ER} \cdot E</math>
:<math>E_{\mathit{eff}} = {\rm ER} \cdot E</math>


where <math>E_{\mathit{eff}}</math> is the effective efficiency for the pump (kW/kW), accounting for slurry derating of the efficiency estimated from the characteristic curve.
where <math>E_{\mathit{eff}}</math> is the effective efficiency for the pump (kW/kW), accounting for slurry derating of the efficiency estimated from the characteristic curve.


The efficiency ratio is sometimes reported to be approximately equal to the head ratio. {{Engin and Gur (2003)}} Alternatively, the Warman nomograph provides a method for estimating the efficiency ratio based on the head ratio and volume fraction solids of the slurry (Figure 3, bottom right).
The efficiency ratio is sometimes reported to be approximately equal to the head ratio. {{Engin and Gur (2003)}}  
 
Alternatively, the Warman nomograph provides a method for estimating the efficiency ratio based on the head ratio and volume fraction solids of the slurry (Figure 3, bottom right). The updated Weir / HI method also applies the same Warman nomograph approach.
 
</hide><div class="user-show">


=== Motor Power ===
=== Motor Power ===
</div><hide>


The power drawn by the pumping duty at the drive shaft, <math>P_{\rm shaft}</math> (kW), is:{{King (2002)}}
The power drawn by the pumping duty at the drive shaft, <math>P_{\rm shaft}</math> (kW), is:{{King (2002)}}


:<math>P_{\rm shaft} = \dfrac{Q \cdot \rho_{\rm SL} \cdot g \cdot H_{\rm t}}{E \cdot \mathit{ER}}</math>
:<math>P_{\rm shaft} = \dfrac{Q \cdot \rho_{\rm SL} \cdot g \cdot H_{\rm t}}{E \cdot {\rm ER}}</math>


Due to electrical and mechanical inefficiencies, the power drawn by the motor, <math>P_{\rm motor}</math> (kW), is:
Due to electrical and mechanical inefficiencies, the power drawn by the motor, <math>P_{\rm motor}</math> (kW), is:
Line 195: Line 249:
where <math>\eta</math> is the motor factor (kW/kW).
where <math>\eta</math> is the motor factor (kW/kW).


</hide><div class="user-show">
=== Froth Volume Factor ===
=== Froth Volume Factor ===
</div><hide>


When determining pump performance, the volumetric flow rate of slurry may need to be adjusted for the presence of ''froth'':{{Weir (2009b)}}
When determining pump performance, the volumetric flow rate of slurry may need to be adjusted for the presence of ''froth'':{{Weir (2009b)}}


:<math>Q = \mathit{FVF} \cdot \big [(Q_{\rm V})_{\rm S} + (Q_{\rm V})_{\rm L} \big ]</math>
:<math>Q = {\rm FVF} \cdot \big [(Q_{\rm V})_{\rm S} + (Q_{\rm V})_{\rm L} \big ]</math>


where:
where:
* <math>\mathit{FVF}</math> is the Froth Volume Factor, the ratio of frothed slurry volume to the original (un-frothed) slurry volume (v/v)
* <math>{\rm FVF}</math> is the Froth Volume Factor, the ratio of frothed slurry volume to the original (un-frothed) slurry volume (v/v)
* <math>(Q_{\rm V})_{\rm S}</math> and <math>(Q_{\rm V})_{\rm L}</math> are the volumetric flow rates of solids and liquids, respectively, in the slurry (m<sup>3</sup>/s)
* <math>(Q_{\rm V})_{\rm S}</math> and <math>(Q_{\rm V})_{\rm L}</math> are the volumetric flow rates of solids and liquids, respectively, in the slurry (m<sup>3</sup>/s)


Slurry density is similarly adjusted:
Slurry density is similarly adjusted:


:<math>\rho_{\rm F} = \dfrac{\rho_{\rm SL}}{\mathit{FVF}}</math>
:<math>\rho_{\rm F} = \dfrac{\rho_{\rm SL}}{{\rm FVF}}</math>


where <math>\rho_{\rm F}</math> (t/m<sup>3</sup>) is the density of the frothed slurry, used in place of <math>\rho_{\rm SL}</math> in the pump performance equations when froth is present.
where <math>\rho_{\rm F}</math> (t/m<sup>3</sup>) is the density of the frothed slurry, used in place of <math>\rho_{\rm SL}</math> in the pump performance equations when froth is present.


</hide><div class="user-show">
=== Settling velocity ===
=== Settling velocity ===
</div><hide>


The settling velocity of a heterogenous slurry can be estimated by using the Durand equation:{{Dunne et al. (2019)}}
The settling velocity of a heterogenous slurry can be estimated by using the Durand equation:{{Dunne et al. (2019)}}
Line 223: Line 281:
The settling velocity may be compared to the actual pipe velocity to asses whether settling may be an issue for the application in question.
The settling velocity may be compared to the actual pipe velocity to asses whether settling may be an issue for the application in question.


</hide><div class="user-show">
=== Pumps in series and parallel ===
=== Pumps in series and parallel ===
</div><hide>


Centrifugal pumps configured in '''series''' (stages) add the total head capability of each individual pump:
Centrifugal pumps configured in '''series''' (stages) add the total head capability of each individual pump:
Line 246: Line 306:


Note that the assumption of identical performance for pumps within series or parallel configurations is a major simplification, which may not be strictly valid in practice due to differing piping system properties, pump wear, control configuration etc.
Note that the assumption of identical performance for pumps within series or parallel configurations is a major simplification, which may not be strictly valid in practice due to differing piping system properties, pump wear, control configuration etc.
</hide>


== Excel ==
== Excel ==
Line 281: Line 342:
\rho_{\rm L}\text{ (t/m}^\text{3}\text{)}\\
\rho_{\rm L}\text{ (t/m}^\text{3}\text{)}\\
d_{50}\text{ (m)}\\
d_{50}\text{ (m)}\\
\mathit{FVF}\text{ (v/v)}\\
{\rm FVF}\text{ (v/v)}\\
\mu\text{ (Pa.s)}\\
\mu\text{ (Pa.s)}\\
H_{\rm s}\text{ (m)}\\
H_{\rm s}\text{ (m)}\\
Line 291: Line 352:
N\text{ (Hz)}\\
N\text{ (Hz)}\\
f\\
f\\
\mathit{HR}\text{ (m/m)}\\
{\rm HR}\text{ (m/m)}\\
\mathit{ER}\text{ (kW/kW)}\\
{\rm ER}\text{ (kW/kW)}\\
F_{\rm L}\\
F_{\rm L}\\
C_{\rm fp}\text{ (frac)}\\
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\;\;\;\;\;\;


Line 312: Line 374:
H_{\rm e}\text{ (m)}\\
H_{\rm e}\text{ (m)}\\
H_{\rm t}\text{ (m)}\\
H_{\rm t}\text{ (m)}\\
\mathit{HR}\text{ (m/m)}\\
{\rm HR}\text{ (m/m)}\\
H_{\rm w}\text{ (m)}\\
H_{\rm w}\text{ (m)}\\
N\text{ (Hz)}\\
N\text{ (Hz)}\\
Line 318: Line 380:
N_{\rm Q}\\
N_{\rm Q}\\
E\text{ (kW/kW)}\\
E\text{ (kW/kW)}\\
\mathit{ER}\text{(kW/kW)}\\
{\rm ER}\text{(kW/kW)}\\
P_{\rm shaft}\text{ (kW)}\\
P_{\rm shaft}\text{ (kW)}\\
P_{\rm motor}\text{ (kW)}\\
P_{\rm motor}\text{ (kW)}\\
Line 328: Line 390:
* <math>\text{Model mode}</math> indicates whether the pump model returns the flow rate at a given speed or the speed at a given flow rate, where <br>''0 = Calculate speed at flow rate, 1 = Calculate flow rate at speed''
* <math>\text{Model mode}</math> indicates whether the pump model returns the flow rate at a given speed or the speed at a given flow rate, where <br>''0 = Calculate speed at flow rate, 1 = Calculate flow rate at speed''
* <math>\text{f method}</math> is the friction factor estimation method, ''0 = User, 1 = Colebrook, 2 = Churchill''
* <math>\text{f method}</math> is the friction factor estimation method, ''0 = User, 1 = Colebrook, 2 = Churchill''
* <math>\text{HR method}</math> is the head ratio estimation method, ''0 = User, 1 = Cave, 2 = Warman''
* <math>\text{HR method}</math> is the head ratio estimation method, ''0 = User, 1 = Cave, 2 = Warman, 3 = Weir / HI''
* <math>\text{ER method}</math> is the efficiency ratio estimation method, ''0 = User, 1 = ER equals HR, 2 = Warman''
* <math>\text{ER method}</math> is the efficiency ratio estimation method, ''0 = User, 1 = ER equals HR, 2 = Warman, 3 = Weir / HI''
* <math>\text{FL method}</math> is the Durand factor estimation method, ''0 = User, 1 = Equation''
* <math>\text{FL method}</math> is the Durand factor estimation method, ''0 = User, 1 = Equation''
* <math>(Q_{\rm M})_{\rm S}</math> is the mass flow rate of solids through the pump (kg/s)
* <math>(Q_{\rm M})_{\rm S}</math> is the mass flow rate of solids through the pump (kg/s)
Line 353: Line 415:
The sections and variable names used in the SysCAD interface are described in detail in the following tables.
The sections and variable names used in the SysCAD interface are described in detail in the following tables.


==== {{Name (Text, Company Name)|nospace=1}}*Pump page ====
==== {{SysCAD (Text, UnitType Prefix)}}Pump page ====


The first tab page in the access window will have this name.
The first tab page in the access window will have this name.
Line 422: Line 484:
|Flow Rate
|Flow Rate
|The model calculates the pump flow rate at the user-specified speed and head.
|The model calculates the pump flow rate at the user-specified speed and head.
<!--
|- style="vertical-align:top;"
|- style="vertical-align:top;"
|TransferPull
|TransferPull
Line 429: Line 492:
* Sets the pump to SysCAD ''Transfer Pull'' mode, where material is drawn from an upstream surge unit (e.g. tank) at the calculated pump flowrate (Q).
* Sets the pump to SysCAD ''Transfer Pull'' mode, where material is drawn from an upstream surge unit (e.g. tank) at the calculated pump flowrate (Q).
* See [https://help.syscad.net/Simulation_Modes SysCAD Simulation Modes] for more information.
* See [https://help.syscad.net/Simulation_Modes SysCAD Simulation Modes] for more information.
-->
|-
|-
! colspan="3" style="text-align:left;" |''CharacteristicCurve''
! colspan="3" style="text-align:left;" |''CharacteristicCurve''
Line 566: Line 630:
! colspan="3" style="text-align:left;" |''HeadRatio''
! colspan="3" style="text-align:left;" |''HeadRatio''
|- style="vertical-align:top;"
|- style="vertical-align:top;"
|rowspan="3" | Method
|rowspan="4" | Method
|User Defined
|User Defined
|The head ratio is specified by the user.
|The head ratio is specified by the user.
Line 575: Line 639:
|Warman
|Warman
|The Warman method is used to estimate the head ratio.
|The Warman method is used to estimate the head ratio.
|- style="vertical-align:top;"
|Weir / HI
|The Weir / HI method is used to estimate the head ratio.
|-
|-
|HeadRatio / HR
|HeadRatio / HR
Line 586: Line 653:
! colspan="3" style="text-align:left;" |''EfficiencyRatio''
! colspan="3" style="text-align:left;" |''EfficiencyRatio''
|- style="vertical-align:top;"
|- style="vertical-align:top;"
|rowspan="3" | Method
|rowspan="4" | Method
|User Defined
|User Defined
|The efficiency ratio is specified by the user.
|The efficiency ratio is specified by the user.
Line 595: Line 662:
|Warman
|Warman
|The Warman method is used to estimate the efficiency ratio.
|The Warman method is used to estimate the efficiency ratio.
|- style="vertical-align:top;"
|Weir / HI
|The Weir / HI method is used to estimate the efficiency ratio.
|-
|-
|EfficiencyRatio / ER
|EfficiencyRatio / ER
Line 622: Line 692:
|-
|-
! colspan="3" style="text-align:left;" |''Speed''
! colspan="3" style="text-align:left;" |''Speed''
|- style="vertical-align:top;"
|Iterations
|style="vertical-align:top;background: #eaecf0" |Display
|The number of internal model iterations required to resolve any dependence between friction head and pump flow rate.
Only applicable when ''CalculationMode = Flow Rate''.
|-
|-
|N
|N
Line 659: Line 734:


{{SysCAD (Page, About)}}
{{SysCAD (Page, About)}}
== External links ==
* [https://help.syscad.net/Met_Dynamics_-_Pump Met Dynamics - Pump (help.syscad.net)]
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Crushing_and_Grinding_Example Crushing and Grinding Example project (help.syscad.net)]
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Crushing,_Grinding_and_Flotation_Example Crushing, Grinding and Flotation Example project (help.syscad.net)]
* [https://help.syscad.net/Met_Dynamic_-_Dynamic_Example_Projects#Dynamic_Grinding_Example Dynamic Grinding Example project (help.syscad.net)]


== References ==
== References ==

Latest revision as of 15:16, 27 June 2025

Description

The article describes a method for estimating the performance of a centrifugal slurry pump.

Centrifugal pumps are a critical component of metallurgical processing plants. The transport of solid particles in slurries presents additional complexity, as pumps are typically tested and rated for water duties only.

The centrifugal slurry pump modelling approach described below has the following features:

  • The reduction of typical vendor pump performance curves into generalised mathematical relationships for computational implementation
  • The de-rating of water duty pump performance for heterogenous slurries
  • Estimation of the effects of elevation, piping system properties and transport destination processing equipment (e.g. hydrocyclones)
  • An estimation of the settling velocity of slurries during transport

Note that the centrifugal slurry pump model described here is not intended to replace the more comprehensive design methods and tools currently available. Rather, it is intended to provide the user with a comparatively simpler tool which can be integrated with other unit models and provide useful estimates of pump speed, flow rate, motor power, and pressure head in the broader context of a mineral processing circuit. More sophisticated methods should be applied for engineering design or optimisation.

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Generalised characteristic curves

Speed

Efficiency

Total dynamic head

Friction factor

Head ratio

Cave method

Warman method

Weir / HI method

Efficiency ratio

Motor Power

Froth Volume Factor

Settling velocity

Pumps in series and parallel

Excel

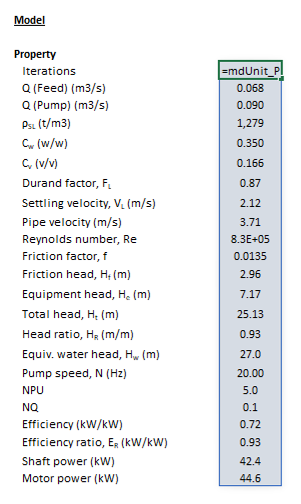
The centrifugal slurry pump model may be invoked from the Excel formula bar with the following function call: 

=mdUnit_Pump_King(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with example images showing the same arrays in the Excel interface:


where:

  • indicates whether the pump model returns the flow rate at a given speed or the speed at a given flow rate, where
    0 = Calculate speed at flow rate, 1 = Calculate flow rate at speed
  • is the friction factor estimation method, 0 = User, 1 = Colebrook, 2 = Churchill
  • is the head ratio estimation method, 0 = User, 1 = Cave, 2 = Warman, 3 = Weir / HI
  • is the efficiency ratio estimation method, 0 = User, 1 = ER equals HR, 2 = Warman, 3 = Weir / HI
  • is the Durand factor estimation method, 0 = User, 1 = Equation
  • is the mass flow rate of solids through the pump (kg/s)
  • is the mass flow rate of liquids through the pump (kg/s)
  • is the number of internal model iterations required to resolve any dependence between friction head and pump flow rate
  • is the actual volumetric flow rate of slurry in the pump feed, computed from , , , and
Figure 4. Example showing the selection of the Parameters (blue frame) array in Excel.
Figure 5. Example showing the Results (light blue frame) array in Excel.

When calculating speed at flow rate ():

  • and the value of is computed by the model and returned.
  • This mode might be used to simulate the operating point of a variable speed pump in a steady state model, for example.

When calculating flow rate at speed ():

  • is a user input and is computed and returned.
  • The return value of may be different to .
  • This might indicate a quantity of make-up water is required to maintain the level of a tank feeding the pump, for example.

SysCAD

The sections and variable names used in the SysCAD interface are described in detail in the following tables.

MD_Pump page

The first tab page in the access window will have this name.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Tag Display This name tag may be modified with the change tag option.
Condition Display OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount Display The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc Display This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.

If this field is blank, then SysCAD will display the unit class ID.

Requirements
On CheckBox This enables the unit. If this box is not checked, then no model calculations or actions are performed.
Options
ShowQIn CheckBox QIn and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream.
ShowQOut CheckBox QOut and associated tab pages (eg Sp) will become visible, showing the properties of the overflow stream.
SizeForPassingFracCalc Input Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section.
FracForPassingSizeCalc Input Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section.
Stream Summary
MassFlow / Qm Display The total mass flow in each stream.
SolidMassFlow / SQm Display The Solids mass flow in each stream.
LiquidMassFlow / LQm Display The Liquid mass flow in each stream.
VolFlow / Qv Display The total Volume flow in each stream.
Temperature / T Display The Temperature of each stream.
Density / Rho Display The Density of each stream.
SolidFrac / Sf Display The Solid Fraction in each stream.
LiquidFrac / Lf Display The Liquid Fraction in each stream.
Passing Display The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream.
Passes Display The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction.

Pump page

The Pump page is used to specify the input parameters for the centrifugal slurry pump model.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Pump
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
Iterations Display Shows the number of internal model iterations (per SysCAD step) required to converge the pump model.
Duty
NumStages Input The number of sequential duplicate pump stages.
NumParallel Input The number of duplicate pumps in parallel.
Config
CalculationMode Speed The model calculates the speed required to pump the volumetric flow rate of the feed stream, at the given head.
Flow Rate The model calculates the pump flow rate at the user-specified speed and head.
CharacteristicCurve
ImpellerDiameter / Dimp Input Diameter of the pump impeller.
AN Input Coefficient of the generalised characteristic curve equation.
BN Input Coefficient of the generalised characteristic curve equation.
CN Input Coefficient of the generalised characteristic curve equation.
EfficiencyCurve
AE Input Coefficient of the generalised efficiency curve equation.
BE Input Coefficient of the generalised efficiency curve equation.
CE Input Coefficient of the generalised efficiency curve equation.
Feed
FrothVolumeFactor / FVF Input Value of the Froth Volume Factor.
VolFlow / Qv Display Volumetric flow of solids and liquids in the pump feed stream, adjusted by the Froth Volume Factor.
SolidDensity / SRho Display Density of solids in the pump feed stream.
Liquids / LRho Display Density of liquids in the pump feed stream.
SlurryDensity / SLRho Display Density of slurry (solids plus liquids) in the pump feed stream.
SolidFrac / Sf Display Mass fraction of solids in the feed stream.
SolidVolFrac / Svf Display Volume fraction of solids in the feed stream.
LViscosity Display Viscosity of liquids in the feed stream.
Userd50 CheckBox Indicates user-specified d50 value. Default is to use d50 computed from the feed stream.
d50 Input/Display Mean size of particles in pump feed.
Head
StaticHead
StaticHead / Hs Input Static head component of the total dynamic head.
FrictionHead
Method User Defined The friction factor is specified by the user.
Colebrook The Colebrook equation is used to estimate the friction factor.
Churchill The Churchill equation is used to estimate the friction factor.
PipeDiameter / D Input Internal diameter of the pipe
EquivPipeLength / L Input Equivalent length of the pipe, including pipe fittings etc.
FrictionFactor / f Input / Display Friction factor used to estimate friction head.
Roughness / k Input Absolute surface roughness of the pipe internal wall.
ReynoldsNumber / Re Display Reynolds Number of the pipe flow stream.
FrictionHead / Hf Display Friction head component of the total dynamic head.
EquipmentHead
EquipmentPressure / Pe Input Pressure drop due to equipment at the end of the pipe.
EquipmentHead / He Display Pressure drop due to equipment at the end of the pipe, converted to head measurement units.
Total head
TotalHead / Ht Display Total dynamic head that the pump acts against. Sum of static, friction and equipment heads.
HeadRatio
Method User Defined The head ratio is specified by the user.
Cave Cave's method is used to estimate the head ratio.
Warman The Warman method is used to estimate the head ratio.
Weir / HI The Weir / HI method is used to estimate the head ratio.
HeadRatio / HR Input / Display Head ratio of the slurry stream.
EquivWaterHead / Hw Display Head of water equivalent to the slurry total dynamic head, as estimated via the head ratio.
EfficiencyRatio
Method User Defined The efficiency ratio is specified by the user.
Equals HR The efficiency ratio is set equal to the value of the head ratio.
Warman The Warman method is used to estimate the efficiency ratio.
Weir / HI The Weir / HI method is used to estimate the efficiency ratio.
EfficiencyRatio / ER Input / Display Efficiency ratio of the slurry stream.
SettlingVelocity
Method User Defined The Durand factor is specified by the user.
Durand The Durand factor is estimated by the Durand equation.
DurandFactor / FL Input / Display Durand factor to be used in the Durand equation.
SettlingVelocity / VL Display Settling velocity estimated by the Durand equation.
PipeVelocity / V Display Velocity of flow through the pipe at pump flow rate, Q.
Speed
Iterations Display The number of internal model iterations required to resolve any dependence between friction head and pump flow rate.

Only applicable when CalculationMode = Flow Rate.

N Input / Display Rotational speed of the pump.
Q Display Volumetric flow rate of the pump at the given speed and head.
HeadNumber / NPU Display Dimensionless pump head number used in calculations.
FlowNumber / NQ Display Dimensionless pump flow number used in calculations.
Power
MotorFactor / Eta Input Efficiency factor of the pump. Fraction of power input to the motor which is useable by the pump at the shaft to move fluid.
Efficiency / E Display Efficiency of the pump.
ShaftPower / PShaft Display Power drawn by the pump at the shaft.
MotorPower / PMotor Display Power drawn by the pump motor, including inefficiencies.

About page

This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
About
HelpLink ButtonLicensingHelp.png Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required.
Information ButtonCopyToClipboard.png Copies Product and License information to the Windows clipboard.
Product
Name Display Met Dynamics software product name
Version Display Met Dynamics software product version number.
BuildDate Display Build date and time of the Met Dynamics Models SysCAD Add-On.
License
File ButtonBrowse.png This is used to locate a Met Dynamics software license file.
Location Display Type of Met Dynamics software license or file name and path of license file.
SiteCode Display Unique machine identifier for license authorisation.
ReqdAuth Display Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime.
Status Display License status, LICENSE_OK indicates a valid license, other messages report licensing errors.
IssuedTo Display Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to.
ExpiryDate Display Only visible if Met Dynamics license file is used. License expiry date.
DaysLeft Display Only visible if Met Dynamics license file is used. Days left before the license expires.

External links

References

Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Pump_(Centrifugal,_Slurry)&oldid=3173"