Properties (Bulk Density)

Description

This article describes the Evertsson (1999) method for estimating the dry bulk density of a polydisperse particle ensemble.

The Evertsson method was derived for cone crusher products, but the relationships may also be applicable in similar mineral processing and materials handling contexts, e.g. conveyors and bins, screen or HPGR feed etc.

Model theory

This content is available to registered users. Please log in to view.

Excel

The Evertsson bulk density estimation may be invoked from the Excel formula bar with the following function call:

=mdProps_BulkDensity_Evertsson(MeanSize as Range, Stream as Range, SG as Range, Optional returnPackFrac as Boolean = false)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

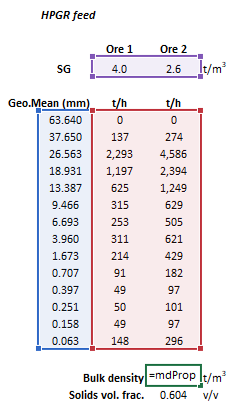
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:

${\begin{aligned}MeanSize&={\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{31}{\text{ (mm)}}\\\end{bmatrix}}\\\\{\mathit {Stream}}&={\begin{bmatrix}(Q_{\rm {M}})_{11}{\text{ (t/h)}}&\dots &(Q_{\rm {M}})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{\rm {M}})_{n1}{\text{ (t/h)}}&\dots &(Q_{\rm {M}})_{nm}{\text{ (t/h)}}\\\end{bmatrix}}\\\\{\mathit {SG}}&={\begin{bmatrix}(\rho _{\rm {S}})_{1}{\text{ (t/m}}^{\text{3}}{\text{)}}&\dots &(\rho _{\rm {S}})_{m}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\end{bmatrix}}\\\\{\mathit {returnPackFrac}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}$ ${\mathit {mdProps\_BulkDensity\_Evertsson}}={\begin{bmatrix}\rho _{\rm {Bulk}}{\text{ (t/m}}^{\text{3}}{\text{)}}^{*}{\text{ or }}\rho _{\aleph }{\text{ (v/v)}}^{*}\\\end{bmatrix}}$ where: ${\mathit {returnPackFrac}}$ indicates whether to return the packing fraction (i.e. solids volume fraction, $\rho _{\aleph }$) of particles in the stream (v/v). Default is to return the bulk density (t/m3) the superscript $^{*}$ indicates an optionally-returned value

Figure 1. Example showing the selection of the MeanSize (blue frame), Stream (red frame), SG (purple frame), and Results (green frame) arrays in Excel.