Description
This article describes the Kuznetsov–Cunningham–Ouchterlony (KCO) model (Ouchterlony, 2005) for predicting rock fragmentation by blasting.[1]
Model theory
Swebrec distribution

Figure 1. Schematic of blast design geometry (after Bergman, 2005).
[2]The KCO model links blasting conditions to the particle size distribution of fragmented rock via the three-parameter Swebrec function:
![{\displaystyle P_{i}={\dfrac {1}{1+\left[{\dfrac {\ln \left({\dfrac {x_{\rm {max}}}{d_{i}}}\right)}{\ln \left({\dfrac {x_{\rm {max}}}{x_{50}}}\right)}}\right]^{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a710659c0e1d32749f21ed00284b5ae0e059cf19)
where:
 is the index of the size interval,
is the index of the size interval,  ,
,  is the number of size intervals
is the number of size intervals is the cumulative fraction passing size interval
is the cumulative fraction passing size interval 
 is the size of the square mesh interval that mass is retained on (mm)
is the size of the square mesh interval that mass is retained on (mm) , i.e. descending size order from top size (
, i.e. descending size order from top size ( ) to sub mesh (
) to sub mesh ( mm)
mm) is the maximum (top) size of the distribution, i.e. the maximum block size (mm)
is the maximum (top) size of the distribution, i.e. the maximum block size (mm) is the mean size (passing 50%) of the distribution (mm)
is the mean size (passing 50%) of the distribution (mm) is a curve-undulation exponent.
is a curve-undulation exponent.
Figure 1 outlines the primary blast design dimensions relevant to the KCO model.
Maximum block size, xmax
The maximum block size is the smallest value of the in situ block size, the blast-hole burden,  , and the spacing,
, and the spacing,  , (m), i.e.:
, (m), i.e.:

Mean size parameter, x50
The mean size of the distribution,  (mm), is estimated by:
(mm), is estimated by:

where:
 is the rock mass factor
is the rock mass factor is the charge weight per hole (kg)
is the charge weight per hole (kg) is the explosive’s weight strength relative to ANFO (%)
is the explosive’s weight strength relative to ANFO (%) is the specific charge (kg/m3)
is the specific charge (kg/m3) is assumed
is assumed- The 10 factor converts Ouchterlony's centimetre units to millimetres.
The rock mass factor,  is:
is:

The rock mass description, , is:
, is:

The joint factor,  ,
,

where the joint plane spacing,  , is related to the aversge joint spacing,
, is related to the aversge joint spacing,  (m), by:
(m), by:

The joint plane angle,  , is:
, is:

The rock density influence,  , is:
, is:

where  is the rock density (kg/m3).
is the rock density (kg/m3).
The hardness factor,  , is:
, is:

where  is Young's Modulus (GPa) and
is Young's Modulus (GPa) and  is the compressive strength of the rock (MPa).
is the compressive strength of the rock (MPa).
Curve-undulation exponent, b
The curve-undulation exponent  is determined from:
is determined from:
![{\displaystyle b=\left[2\ln 2\cdot \ln \left({\dfrac {x_{\rm {max}}}{x_{50}}}\right)\right]\cdot n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caba0555eba9f3cac3ae991dbe58bf40720c9081)
where:
![{\displaystyle n=\left(2.2-{\dfrac {0.014B}{\varnothing _{\rm {h}}}}\right)\cdot \left(1-{\dfrac {\mathit {SD}}{B}}\right)\cdot {\sqrt {\dfrac {\left(1+{\dfrac {S}{B}}\right)}{2}}}\cdot \left[{\dfrac {\left\vert L_{\rm {b}}-L_{\rm {c}}\right\vert }{L_{\rm {tot}}}}+1\right]^{0.1}\cdot \left({\dfrac {L_{\rm {tot}}}{H}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8244d98f277de68aa1be370af3ec55a0c0ab89bc)
and:
 is the drill-hole diameter (m)
is the drill-hole diameter (m) is the length of bottom charge (m)
is the length of bottom charge (m) is the length of column charge (m)
is the length of column charge (m) is the total charge length (m)
is the total charge length (m) is the bench height or hole depth (m)
is the bench height or hole depth (m) is the standard deviation of drilling accuracy (m).
is the standard deviation of drilling accuracy (m).
Excel
The KCO blasting model may be invoked from the Excel formula bar with the following function call:
=mdUnit_Blasting_KCO(Parameters as Range, Size as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row ( ) x column (
) x column ( ) format:
) format:

Results
The results are displayed in Excel as an array corresponding to the matrix notation below:

Example
The images below show the selection of input arrays and output results in the Excel interface.
 Figure 1. Example showing the selection of the Parameters (blue frame) array in Excel. |
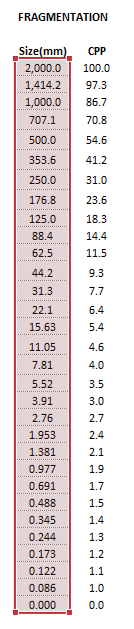 Figure 2. Example showing the selection of the Size (red frame) array in Excel. |
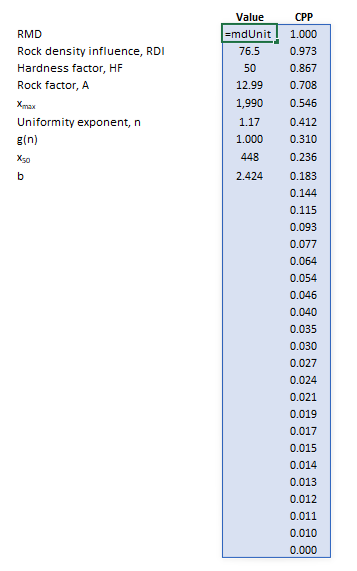 Figure 3. Example showing the selection of the Results (light blue frame) array in Excel. |
See also
References
- ↑ Ouchterlony, F., 2005. The Swebrec© function: linking fragmentation by blasting and crushing. Mining Technology, 114(1), pp.29-44.
- ↑ Bergman, P., 2005. Optimisation of fragmentation and comminution at Boliden Mineral, Aitik Operation (Doctoral dissertation, Luleå tekniska universitet).

![{\displaystyle P_{i}={\dfrac {1}{1+\left[{\dfrac {\ln \left({\dfrac {x_{\rm {max}}}{d_{i}}}\right)}{\ln \left({\dfrac {x_{\rm {max}}}{x_{50}}}\right)}}\right]^{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a710659c0e1d32749f21ed00284b5ae0e059cf19)




































![{\displaystyle b=\left[2\ln 2\cdot \ln \left({\dfrac {x_{\rm {max}}}{x_{50}}}\right)\right]\cdot n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caba0555eba9f3cac3ae991dbe58bf40720c9081)
![{\displaystyle n=\left(2.2-{\dfrac {0.014B}{\varnothing _{\rm {h}}}}\right)\cdot \left(1-{\dfrac {\mathit {SD}}{B}}\right)\cdot {\sqrt {\dfrac {\left(1+{\dfrac {S}{B}}\right)}{2}}}\cdot \left[{\dfrac {\left\vert L_{\rm {b}}-L_{\rm {c}}\right\vert }{L_{\rm {tot}}}}+1\right]^{0.1}\cdot \left({\dfrac {L_{\rm {tot}}}{H}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8244d98f277de68aa1be370af3ec55a0c0ab89bc)











