Stirred Mill (Power, Nitta)

Description

This article describes the Nitta method for estimating the power draw of a vertical stirred mill.

Model theory

The Nitta approach computes mill power as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm net} = \eta P_{\rm gross} = K \cdot \left [ H (J_{\rm b} - J_{\rm s}) \right ]^{0.884} S^{2.232} D_{\rm G} N^{1.232}}

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm net}} is the net power draw of the mill, i.e. excluding mill drive losses (kW)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm gross}} is the gross power draw of the mill, i.e. including mill drive losses (kW)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} is the mill drive efficiency (kW/kW)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} is the power constant (kW), Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=312} suggested.
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} is mill height (m)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{\rm b}} is the fraction of mill volume occupied by the media charge, void space and stirrer below the charge level (v/v).
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{\rm s}} is the fraction of mill volume occupied by the stirrer below the level of the media charge (v/v).
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} is the diameter of the stirrer (m)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_{\rm G}} is the gap between the inside wall of the mill and the stirrer (m)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} is the rotational speed of the stirrer (rps)

Adopting a similar approach as the Hogg and Fuerstenau tumbling mill power model, the net power draw, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm net}} , may be separated into its contributing constituents:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm b} = \left ( \frac{(1-f_{\rm v}) \rho_{\rm b} }{\rho_{\rm ap}} \right ) \cdot P_{\rm net}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm s} = \left ( \frac{\rho_{\rm p} f_{\rm v} }{\rho_{\rm ap}} \right ) \cdot P_{\rm net}}

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm b}} is the power drawn by the ball component of the mill load (kW)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{\rm s}} is the power drawn by the interstitial slurry component of the mill load (kW)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\rm v}} is the volumetric fraction of interstitial void space in the charge (usually 0.4) (v/v)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm b}} is the density of balls (t/m³)

The apparent charge density, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm ap}} , may be computed as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm ap} = (1-f_{\rm v}) \rho_{\rm b} + \rho_{\rm p} f_{\rm v}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm p}} is the density of slurry (t/m³).

The slurry density, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm p}} , may be computed as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm p} = \dfrac{1}{\dfrac{f_{\rm s}}{\rho_{\rm m}} + (1-f_{\rm s})}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{\rm s}} is the mass fraction of solids in the slurry (w/w), and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm m}} is the densityy of solid ore particles (t/m³).

Additional notes

The Nitta model does not include a term for charge density, which may compromise its ability to predict mill power draw with alternative grinding media materials, ore densities or feed solids fractions.

Excel

The Nitta mill power model may be invoked from the Excel formula bar with the following function call:

=mdMillPower_Nitta(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

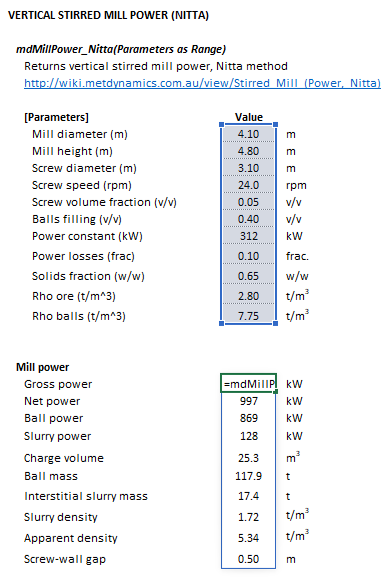
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Parameters= \begin{bmatrix} D\text{ (m)}\\ H\text{ (m)}\\ S\text{ (m)}\\ N\text{ (rpm)}\\ J_{\rm s}\text{ (v/v)}\\ J_{\rm b}\text{ (v/v)}\\ K\text{ (kW)}\\ (1-\eta)\text{ (kW/kW)}\\ f_{\rm s}\text{ (w/w)}\\ \rho_{\rm m}\text{ (t/m}^{\text{3}}\text{)}\\ \rho_{\rm b}\text{ (t/m}^{\text{3}}\text{)}\\ \end{bmatrix},\;\;\;\;\;\; mdMillPower\_Nitta= \begin{bmatrix} P_{\rm gross}\text{ (kw)}\\ P_{\rm net}\text{ (kw)}\\ P_{\rm b}\text{ (kw)}\\ P_{\rm s}\text{ (kw)}\\ \text{Charge volume (m}^{\text{3}}\text{)}\\ \text{Ball mass (t)}\\ \text{Interstitial slurry mass (t)}\\ \rho_{\rm p}\text{ (t/m}^{\text{3}}\text{)}\\ \rho_{\rm app}\text{ (t/m}^{\text{3}}\text{)}\\ D_{\rm G}\text{ (m)}\\ \end{bmatrix}\;\;\;\;\;\;\;\;\;\;\;\; } where: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Charge volume}} is the volume of the charge (m3) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Ball mass}} is the mass of balls in the mill (t) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Interstitial slurry mass}} is the mass of slurry in the interstitial charge void space (t)

Figure 1. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Nitta power model is an optional calculation for stirred mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Nitta
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
MillDiameter	Input/Display	Diameter of the mill (inside liners).
MillHeight	Input/Display	Height of the mill.
ScrewDiameter	Input/Display	Diameter of the screw stirrer.
ScrewSpeed	Input/Display	Rotational speed of the screw stirrer.
ScrewVolFrac	Input/Display	Volume occupied by screw stirrer as a fraction of mill volume.
BallFilling	Input/Display	Volumetric fraction of the mill filled with balls, including slurry and interstitial voids between balls.
PowerConstant	Input	Coefficient of the power equation.
PowerLosses	Input	Fraction of power lost due to mill drive efficiency (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =1-\eta} ).
SolidsFraction	Display	Mass fraction of solids in the slurry phase.
OreDensity	Display	Density of solids.
BallDensity	Input/Display	Density of balls.
ScrewWallGap	Display	Distance between mill wall and screw stirrer.
ChargeVolume	Display	Volume of media charge in the mill.
BallMass	Display	Mass of balls in the mill.
InterstitialSLMass	Display	Mass of slurry occupying charge void space.
RhoSlurry	Display	Density of slurry phase.
ApparentDensity	Display	Density of total charge (including balls, slurry and voids).
BallsPower	Display	Power drawn by the ball component of the mill load.
SlurryPower	Display	Power drawn by the interstitial slurry component of the mill load.
NetPower	Display	Net power drawn by the mill (excluding drive inefficiencies).
GrossPower	Display	Gross power drawn by the mill (including drive inefficiencies).

See also

• Mill (Herbst-Fuerstenau)
• Ball Mill (Perfect Mixing)
• Ball Mill (Perfect Mixing, Dynamic)