Flotation Cell (Savassi)

Description

This article describes a model that estimates the recovery of ore and gangue from a mechanical flotation cell.

The approach is outlined by Savassi (2005), who proposed a compartment model that separates the mechanisms of true flotation, froth recovery, and entrainment.

Savassi's original model was further extended over many years by subsequent researchers, and the resulting methodology is frequently referred to as the "P9 model" in reference to the AMIRA P9 project that has driven much of the development since.

Model theory

Floatability classes

Much of the original literature underpinning the modelling approach described here refers to the notion of a floatability class, which groups all particles that exhibit similar floatability properties, without any particular reference to particle sizes or mineral compositions within the class. In order to align the flotation modelling approach with the comminution, classification and concentration processes described in other articles, a distinction is made between particle size and floatability component.

The mathematical relations below are developed on the basis of a particle size class which is further subdivided into floatability components. This allows the definition of floatability rate groups (e.g. fast, slow, non-floating) within mineral types (e.g. chalcopyrite, pyrite, non-sulphide gangue), by size fraction.

Recovery

Savassi's compartment model describes the recovery of particles by the mechanisms of true flotation, froth mass transfer and entrainment.

The compartment model may be formulated for both batch/plug flow and continuous (perfectly mixed) flow patterns.

Recovery is expressed as:

$R_{ij}={\begin{cases}1-\exp {\big [}-P_{ij}\cdot (S_{b}\cdot 60)\cdot Rf_{ij}\cdot C_{ij}\cdot \tau \cdot (1-ENT_{ij}\cdot R_{w}){\big ]}&{\text{for batch or plug flow flotation}}\\\\{\dfrac {P_{ij}\cdot (S_{b}\cdot 60)\cdot Rf_{ij}\cdot C_{ij}\cdot \tau \cdot (1-R_{w})+ENT_{ij}\cdot R_{w}}{(1+P_{ij}\cdot (S_{b}\cdot 60)\cdot Rf_{ij}\cdot C_{ij}\cdot \tau )(1-R_{w})+ENT_{ij}\cdot R_{w}}}&{\text{for continuous flotation}}\\\end{cases}}$

where:

• $i$ is the index of the size interval, $i=\{1,2,\dots ,n\}$, $n$ is the number of size intervals
• $j$ is the index of the floatability component, $j=\{1,2,\dots ,m\}$, $m$ is the number of floatability components (e.g. mineral types, fast/slow types etc.)
• $R_{ij}$ is the fraction of particles of size fraction $i$ and floatability component type $j$ recovered to concentrate (frac)
• $P_{ij}$ is the floatability of particles of size $i$ and floatability component type $j$ (min^-1)
• $S_{b}$ is the bubble surface area flux (m²/s/m²)
• $Rf_{ij}$ is the fraction of particles of size $i$ and floatability component $j$ recovered by froth (frac)
• $C_{ij}$ is a cell scale-up factor that relates flotation performance between cells of different sizes (e.g. laboratory versus industrial) (frac)
• $\tau$ is the residence time of slurry in the cell (min)
• $ENT_{ij}$ is the fraction of particles of size $i$ and floatability component $j$ recovered by entrainment (frac)
• $R_{w}$ is the fraction of feed water recovered to concentrate (frac)

The cell scale-up factor, $C_{ij}$, is suggested by Yianatos et al. (2010) to allow for the simulation of industrial-scale cells using kinetic rates derived from laboratory cells.

Pulp volume

Pulp volume, $V_{effective}$ (m³), is related to cell paramters.

$V_{effective}=(V_{cell}-V_{mechanism}-A_{cell}*H_{f})\cdot (1-\epsilon _{gas})$

where:

• $V_{cell}$ is the total volume of the cell
• $V_{mechanism}$ is the volume of the impeller mechanism in the cell (m³)
• $A_{cell}$ is the cross sectional area of the cell (m²)
• $H_{f}$ is the froth depth from the top of the cell (m)
• $\epsilon _{gas}$ is the gas hold-up in the pulp (v/v)

Gas hold-up

Gas hold-up, $\epsilon _{gas}$ (v/v), may be estimated from a linear relationship as suggested by the findings of Gorain et al. (1995):

$\epsilon _{gas}=m_{gas}\cdot J_{g}+C_{gas}$

where $m_{gas}$ and $C_{gas}$ are the slope an intercept parameters, respectively, of the linear equation.

The superficial gas rate, $J_{g}$ (m/s), is approximated by:

$J_{g}={\dfrac {Q_{air}}{A_{cell}\cdot 60\cdot 60}}$

where $Q_{air}$ is the air rate (m³/h).

Residence time

Residence time, $\tau$ (min), may be computed on the basis of the cell feed or tailing stream volumetric flow rates.

$\tau ={\begin{cases}{\dfrac {V_{effective}}{Q_{feed}\cdot 60}}&{\text{for feed-based residence time}}\\\\{\dfrac {V_{effective}}{Q_{tail}\cdot 60}}&{\text{for tail-based residence time}}\\\end{cases}}$

where ${Q_{feed}}$ and ${Q_{tail}}$ are the volumetric flow rates of pulp in the feed and tail streams, respectively (m³/h).

The volumetric flow rate of the tailing stream is a function of the recoveries of solids computed by the Savassi equation and water. As such, an iterative procedure is required to estimate the tail-based residence time.

Bubble surface area flux

The bubble surface area flux, $S_{b}$ (m²/s/m²), is related to the superficial gas rate, $J_{g}$, and Sauter mean bubble diameter, $d_{b}$ (m), by the equation:

$S_{b}={\dfrac {6J_{g}}{d_{b}}}$

The Sauter mean bubble diameter may be determined from gas dispersion measurements. Where a measurement of $d_{b}$ is not available, $S_{b}$ may be estimated by the empirical relation of Gorain et al. (1995):

$S_{b}=123{N_{s}}^{0.44}{J_{g}}^{0.75}{As}^{-0.10}{P_{80}}^{-0.42}$

where:

• $N_{s}$ is impeller tip speed (m/s)
• $As$ is impeller aspect ratio (m/m)
• $P_{80}$ is the size that 80% of solid particles in the feed are finer than (µm)

The Gorain relation may be modified to suit alternative bubble surface area flux data sets with:

$S_{b}=C_{Sb}{N_{s}}^{a}{J_{g}}^{b}{As}^{c}{P_{80}}^{d}$

where $C_{Sb}$ and $a\dots d$ are a user-defined coefficient and set of exponents, respectively.

Froth recovery

Froth recovery, $Rf_{ij}$, may be estimated using the froth residence time model outlined by Harris et al. (2002).

$Rf_{ij}=(1-(P_{d})_{j})+(P_{d})_{j}\cdot ENT_{i}\cdot R_{w}$

where $(P_{d})_{j}$ is the probability of detachment of ore type $j$ (frac), computed as:

$(P_{d})_{j}=1-\exp(-\beta _{j}\cdot FRT)$

and $\beta _{j}$ is the detachment rate constant (min^-1) for ore type $j$.

The froth residence time, $FRT$ (min), is computed based on either air or slurry flow rates:

$FRT={\begin{cases}{\dfrac {H_{f}\cdot {\epsilon _{froth}}}{J_{g}}}&{\text{for air-based froth residence time}}\\{\dfrac {H_{f}\cdot A_{cell}\cdot (1-\epsilon _{froth})}{Q_{con}}}&{\text{for slurry-based froth residence time}}\\\end{cases}}$

where $\epsilon _{froth}$ is the gas hold-up fraction in the froth phase (v/v), and $Q_{con}$ is the volumetric flow rate of concentrate from the cell.

The concentrate flow rate, $Q_{con}$, is a function of the recoveries of solids computed by the Savassi equation and water. As with the tail-based residence time (see above), an iterative procedure is required to estimate froth recovery via the froth residence time method (even if a feed-basis is used to estimate pulp residence time).

Entrainment

Entrainment may be estimated by two methods, the hyperbolic equation approach by Savassi et al. (1998), and the froth residence time approach described by Vera et al (2002).

The hyperbolic equation for entrainment is:

$ENT_{i}={\dfrac {2}{\exp \left(2.292\left({\dfrac {{\bar {d}}_{i}}{E20}}\right)^{adj}\right)+\exp \left(-2.292\left({\dfrac {{\bar {d}}_{i}}{E20}}\right)^{adj}\right)}}$

$adj=1+{\dfrac {\ln \delta }{\exp \left({\dfrac {{\bar {d}}_{i}}{E20}}\right)}}$

where:

• ${\bar {d}}_{i}$ is the geometric mean size of particles in size interval $i$ (µm)
• $E20$ is the particle size at which $ENT_{i}$ is 0.2 (µm)
• $\delta$ is the froth drainage parameter

The froth residence time approach first computes the froth residence time ($FRT$) according to the method descibed for froth recovery above. Entrainment is then estimated by applying the following equation:

$ENT_{i}={\dfrac {1}{1+\omega _{i}\cdot FRT}}$

where $\omega _{i}$ is the froth drainage factor for particles in size interval $i$ (min^-1).

Water recovery

Methods for estimating the recovery of water are described by Harris et al. (2002).

The fixed concentrate percent solids method assumes the concentrate is always recovered at a fixed pulp density. The recovery of water, $R_{w}$, is then computed to meet the fixed concentrate solids fraction requirement.

The solids dependent model assumes a power law relationship between the volumetric flow rate of water, $Q_{w}$ (m³/h), and solids, $Q_{s}$ (m³/h), in the concentrate stream:

$Q_{w}=a\cdot {Q_{s}}^{b}$

where $a$ and $b$ are the coefficient and exponent of the power law relationship, respectively.

Finally, the water rate function adopts a first order kinetic relationship between water recovery and pulp residence time:

$R_{w}={\dfrac {k_{w}\tau }{1+k_{w}\tau }}$

where $k_{w}$ is the kinetic rate parameter (min^-1) for the recovery of water to the concentrate stream.

Excel

The Savassi flotation cell model may be invoked from the Excel formula bar with the following function call:

=mdUnit_Flotation_Savassi(Parameters as Range, Size as Range, Feed as Range, OreSG As Range, Floatability as Range, CellScaleUp As Range, DetachRateConst as Range, FrothRecovery as Range, DrainageFactor as Range, Entrainment as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

Inputs

The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row ($i$) x column ($j$) format:

$Parameters={\begin{bmatrix}V_{cell}{\text{ (m}}^{\text{3)}}\\V_{mechanism}{\text{ (m}}^{\text{3)}}\\A_{cell}{\text{ (m}}^{\text{2)}}\\H_{f}{\text{ (m)}}\\Q_{air}{\text{ (m}}^{\text{3}}{\text{/h)}}\\{\text{Gas holdup model}}\\\epsilon _{gas}{\text{ (v/v)}}\\m_{gas}\\C_{gas}\\{\text{Residence time option}}\\{\text{Flow pattern}}\\{\text{Residence time basis}}\\{\text{Sb option}}\\S_{b}{\text{ (m}}^{2}{\text{/s/m}}^{2}{\text{)}}\\{\text{Use calculated P80}}\\P_{80}{\text{ (}}\mu {\text{m)}}\\N_{s}{\text{ (m/s)}}\\A_{s}{\text{ (m/m)}}\\C_{Sb}\\a\\b\\d\\e\\{\text{Froth model}}\\{\text{Froth residence time basis}}\\\epsilon _{froth}{\text{ (v/v)}}\\{\text{Entrainment option}}\\E20{\text{ (}}\mu {\text{m)}}\\\delta \\{\text{FRT entrainment basis}}\\{\text{Water option}}\\{\text{Concentrate fraction solids (w/w)}}\\a_{w}\\b_{w}\\k_{w}\\R_{w}{\text{ (frac)}}\\(Q_{M,F})_{Liquids}{\text{ (t/h)}}\\\rho _{L}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\end{bmatrix}},\;\;\;\;\;\;Size={\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{n}{\text{ (mm)}}\\\end{bmatrix}},\;\;\;\;\;\;Feed={\begin{bmatrix}(Q_{M,F})_{11}{\text{ (t/h)}}&\dots &(Q_{M,F})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{M,F})_{n1}{\text{ (t/h)}}&\dots &(Q_{M,F})_{nm}{\text{ (t/h)}}\\\end{bmatrix}},\;\;\;\;\;\;OreSG={\begin{bmatrix}SG_{1}{\text{ (t/m}}^{\text{3}}{\text{)}}&\dots &SG_{m}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\end{bmatrix}}$

$Floatability={\begin{bmatrix}P_{11}{\text{ (t/h)}}&\dots &P_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\P_{n1}{\text{ (t/h)}}&\dots &P_{nm}{\text{ (t/h)}}\\\end{bmatrix}},\;\;\;\;\;\;CellScaleUp={\begin{bmatrix}C_{11}{\text{ (t/h)}}&\dots &C_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\C_{n1}{\text{ (t/h)}}&\dots &C_{nm}{\text{ (t/h)}}\\\end{bmatrix}},\;\;\;\;\;\;DetachRateConst={\begin{bmatrix}(P_{d})_{1}{\text{ (frac)}}&\cdots &(P_{d})_{m}{\text{ (frac)}}\\\end{bmatrix}},\;\;\;\;\;\;$

$FrothRecovery={\begin{bmatrix}Rf_{11}{\text{ (t/h)}}&\dots &Rf_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\Rf_{n1}{\text{ (t/h)}}&\dots &Rf_{nm}{\text{ (t/h)}}\\\end{bmatrix}},\;\;\;\;\;\;DrainageFactor={\begin{bmatrix}\delta _{1}\\\vdots \\\delta _{n}\\\end{bmatrix}},\;\;\;\;\;\;Entrainment={\begin{bmatrix}ENT_{11}{\text{ (t/h)}}&\dots &ENT_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\ENT_{n1}{\text{ (t/h)}}&\dots &ENT_{nm}{\text{ (t/h)}}\\\end{bmatrix}}$

where:

• ${\text{Gas holdup model}}$ specifies the method used to determine the gas-hold up, 0 = No gas holdup, 1 = User defined, 2 = Jg dependent
• $\epsilon _{gas}$ is the user-defined value of gas hold-up (v/v) if ${\text{Gas holdup model}}=1$, ignored otherwise
• $m_{gas}$ is the value of the slope coefficient if ${\text{Gas holdup model}}=2$, ignored otherwise
• $C_{gas}$ is the value of the slope coefficient if ${\text{Gas holdup model}}=2$, ignored otherwise
• ${\text{Residence time option}}$ specifies the method used to determine the residence time, 0 = User defined, 1 = Calculated
• ${\text{Flow pattern}}$ specifies the cell flow configuration, 0 = Batch or Plug flow, 1 = Perfect Mixing (Continuous)
• ${\text{Residence time basis}}$ specifies the stream which is used to computed the residence time, 0 = Feed, 1 = Tail
• ${\text{Sb option}}$ specifies the method used to determine the bubble surface area, 0 = User defined, 1 = Gorain, 2 = User equation
• $S_{b}$ is the user-defined value of bubble surface area flux (m²/s/m²) if ${\text{Sb option}}=0$, ignored otherwise
• ${\text{Use calculated P80}}$ indicates whether the $P_{80}$ for the Gorain equation (${\text{Sb option}}=1,2$) is user-defined or determined from the feed stream , 0 = User defined, 1 = Calculated P80
• $P_{80}$ is the user-defined value of $P_{80}$ (μm) if ${\text{Sb option}}=1,2$ and ${\text{Use calculated P80}}=1$, ignored otherwise
• $N_{s}$ is the user-defined value of impeller speed (m/s) if ${\text{Sb option}}=1,2$, ignored otherwise
• $A_{s}$ is the user-defined value of impeller aspect ratio (m/m) if ${\text{Sb option}}=1,2$, ignored otherwise
• $C_{Sb}$ is a user-defined coefficient of the Gorain relation if ${\text{Sb option}}=2$, ignored otherwise
• $a\dots d$ are user-defined exponents of the Gorain relation if ${\text{Sb option}}=2$, ignored otherwise
• ${\text{Froth model}}$ specifies the method used to determine froth recovery, 0 = User defined, 1 = FRT
• ${\text{Froth residence time basis}}$ specifies the phase which is used to computed the froth residence time, 0 = Air, 1 = Slurry, if ${\text{Froth model}}=1$, ignored otherwise
• $\epsilon _{froth}$ is the value of the gas hold up fraction (v/v) if ${\text{Froth model}}=1$, ignored otherwise
• ${\text{Entrainment option}}$ specifies the method used to determine entrainment, 0 = No entrainment, 1 = User defined, 2 = Hyperbolic, 3 = FRT dependent
• $E20$ is the value of the hyperbolic equation particle size term (v/v) if ${\text{Entrainment option}}=2$, ignored otherwise
• $\delta$ is the value of the hyperbolic equation drainage factor (v/v) if ${\text{Entrainment option}}=2$, ignored otherwise
• ${\text{FRT entrainment basis}}$ specifies the phase which is used to computed the froth residence time for entrainment, 0 = Air, 1 = Slurry, if ${\text{Entrainment option}}=3$, ignored otherwise
• ${\text{Water option}}$ specifies the method used to determine water recovery, 0 = Fixed % solids, 1 = Solid dependent, 2 = rate function, 3 = User defined
• ${\text{Concentrate fraction solids}}$ is the user-defined value of concentrate pulp density (w/w) if ${\text{Water option}}=0$, ignored otherwise
• $a_{w}$ is a user-defined coefficient if ${\text{Water option}}=1$, ignored otherwise
• $b_{w}$ is a user-defined exponent if ${\text{Water option}}=1$, ignored otherwise
• $k_{w}$ is a user-defined kinetic rate parameter if ${\text{Water option}}=2$, ignored otherwise
• $R_{w}$ is a user-defined water split to concentrate if ${\text{Water option}}=3$, ignored otherwise
• $(Q_{M,F})_{Liquids}$ is the mass flow feed rate of liquids into the cell (t/h)
• $\rho _{L}$ is the specific gravity or density of liquids in the feed (- or t/m³)
• $n$ is the number of size intervals
• $m$ is the number of ore types (floatability classes)
• $d_{i}$ is the size of the square mesh interval that feed mass is retained on (mm)
• $d_{i+1}<d_{i}<d_{i-1}$, i.e. descending size order from top size ($d_{1}$) to sub mesh ($d_{n}=0$ mm)
• $Q_{M,F}$ is the mass flow rate of particles in the feed (t/h)
• $SG$ is the Specific Gravity or density of solids (- or t/m³)

Results

The results are displayed in Excel as an array corresponding to the matrix notation below:

$mdUnit\_Flotation\_Savassi={\begin{bmatrix}{\begin{bmatrix}{\text{Iterations}}\\V_{effective}{\text{ (m}}^{3}{\text{)}}\\J_{g}{\text{ (m/s)}}\\\epsilon _{gas}{\text{ (v/v)}}\\\tau {\text{ (min)}}\\P_{80}{\text{ (}}\mu {\text{m)}}\\S_{b}{\text{ (m}}^{2}{\text{/s/m}}^{2}{\text{)}}\\FRT{\text{ (min)}}\\FRT_{ENT}{\text{ (min)}}\\R_{w}{\text{ (frac)}}\\R{\text{ (frac)}}\\\end{bmatrix}}&{\begin{bmatrix}-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\-&\cdots &-\\\end{bmatrix}}\\{\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{n}{\text{ (mm)}}\end{bmatrix}}&{\begin{bmatrix}(Q_{M,C})_{11}{\text{ (t/h)}}&\dots &(Q_{M,C})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{M,C})_{n1}{\text{ (t/h)}}&\dots &(Q_{M,C})_{nm}{\text{ (t/h)}}\\\end{bmatrix}}\\{\begin{bmatrix}d_{1}{\text{ (mm)}}\\\vdots \\d_{n}{\text{ (mm)}}\end{bmatrix}}&{\begin{bmatrix}(Q_{M,T})_{11}{\text{ (t/h)}}&\dots &(Q_{M,T})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{M,T})_{n1}{\text{ (t/h)}}&\dots &(Q_{M,T})_{nm}{\text{ (t/h)}}\\\end{bmatrix}}\\{\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{n}{\text{ (mm)}}\end{bmatrix}}&{\begin{bmatrix}Rf_{11}{\text{ (frac)}}&\dots &Rf_{1m}{\text{ (frac)}}\\\vdots &\ddots &\vdots \\Rf_{n1}{\text{ (frac)}}&\dots &Rf_{nm}{\text{ (frac)}}\\\end{bmatrix}}\\{\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{n}{\text{ (mm)}}\end{bmatrix}}&{\begin{bmatrix}ENT_{11}{\text{ (frac)}}&\dots &ENT_{1m}{\text{ (frac)}}\\\vdots &\ddots &\vdots \\ENT_{n1}{\text{ (frac)}}&\dots &ENT_{nm}{\text{ (frac)}}\\\end{bmatrix}}\\{\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{n}{\text{ (mm)}}\end{bmatrix}}&{\begin{bmatrix}R_{11}{\text{ (frac)}}&\dots &R_{1m}{\text{ (frac)}}\\\vdots &\ddots &\vdots \\R_{n1}{\text{ (frac)}}&\dots &R_{nm}{\text{ (frac)}}\\\end{bmatrix}}\\{\begin{bmatrix}-\end{bmatrix}}&{\begin{bmatrix}R_{1}{\text{ (frac)}}&\dots &R_{m}{\text{ (frac)}}\end{bmatrix}}\end{bmatrix}}$

where:

• $Iterations$ is the number of iterations required to compute the tails-based residence time
• $FRT_{ENT}$ is the froth residence time (min) calculated for the entrainment method, which may be different to that calculated for froth recovery based on user air/slurry selections
• $R$ is the overall recovery of all solids mass to concentrate (frac), i.e. the mass pull, computed as $\textstyle \sum _{i=1}^{n}{\sum _{j=1}^{m}{R_{ij}}}$
• $Q_{M,C}$ is the mass flow rate of particles in the concentrate stream (t/h)
• $Q_{M,T}$ is the mass flow rate of particles in the tail stream (t/h)
• ${\bar {d}}_{i}$ is the geometric mean size of the internal mesh series interval that mass is retained on (mm)
• $R_{j}$ is the recovery of all solids of ore type $j$ (frac), i.e. the unsized recovery of floatability components

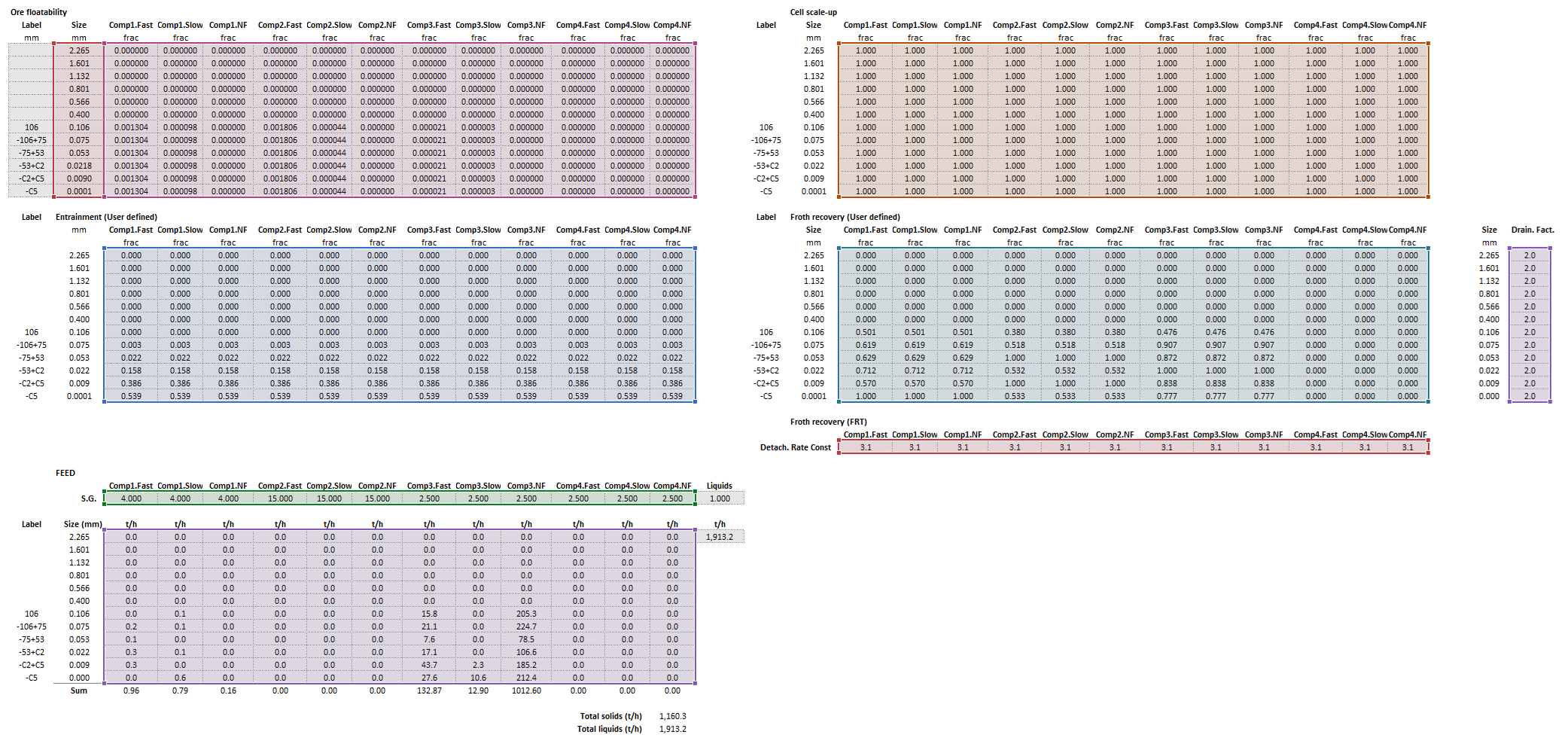
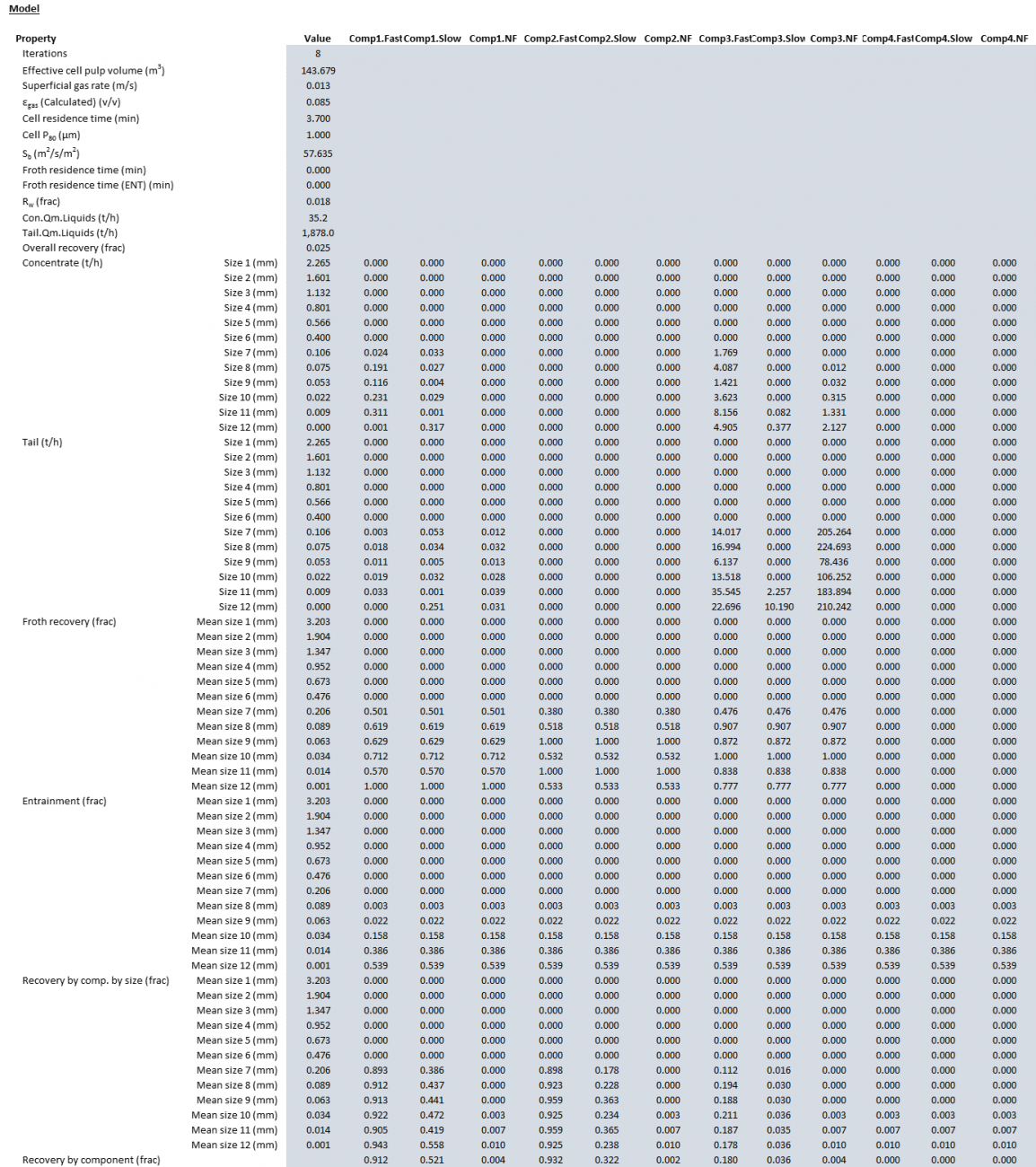
Example

The images below show the selection of input arrays and output results in the Excel interface.

Figure 1. Example showing the selection of the Parameters (blue frame) array in Excel.

Figure 2. Example showing the selection of the Feed (upper purple frame), OreSG (green frame), Floatability (pink frame), CellScaleUp (brown frame), DetachRateConst (teal frame), FrothRecovery (blue frame), DrainageFactor (red frame), and Entrainment (lower purple frame) arrays in Excel.

Figure 3. Example showing the outline of the Results (blue shaded area) array in Excel.

SysCAD

This section is currently under construction. Please check back later for updates and revisions.