Tumbling Mill (Media Trajectory): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
md>Scott.Munro
m (Text replacement - "v_L" to "v_{\rm L}")
imported>Scott.Munro
 
(3 intermediate revisions by 2 users not shown)
Line 14: Line 14:
== Model theory ==
== Model theory ==


{{Restricted content}}
<hide>
[[File:TumblingMillMediaTraj2.png|thumb|625px|Figure 2. Geometric diagram of an outer media element resting on a lifter bar in a tumbling mill at the point of equilibrium (after Powell, 1991).{{Powell (1991)}}]]
[[File:TumblingMillMediaTraj2.png|thumb|625px|Figure 2. Geometric diagram of an outer media element resting on a lifter bar in a tumbling mill at the point of equilibrium (after Powell, 1991).{{Powell (1991)}}]]


Line 32: Line 35:
The equations of motion for each state are summarised below, with reference to the diagrams in Figures 2 and 3. Derivation of the equations is excluded from the summary.
The equations of motion for each state are summarised below, with reference to the diagrams in Figures 2 and 3. Derivation of the equations is excluded from the summary.


</hide><div class="user-show">
=== Point of equilibrium ===
=== Point of equilibrium ===
</div><hide>


At the point of equilibrium, the sum of downward gravitational force, outward radial centrifugal force, normal force of the lifter bar, and frictional force between the lifter surface and the media element is zero.
At the point of equilibrium, the sum of downward gravitational force, outward radial centrifugal force, normal force of the lifter bar, and frictional force between the lifter surface and the media element is zero.
Line 102: Line 107:
:<math>(r_0,\phi_0) =\left ( r_0, \gamma_0 - \beta_0 \right )</math>
:<math>(r_0,\phi_0) =\left ( r_0, \gamma_0 - \beta_0 \right )</math>


</hide><div class="user-show">
=== Lifter bar tip position ===
=== Lifter bar tip position ===
</div><hide>


The position of a media element at tip of the lifter bar is defined by the following parameters:
The position of a media element at tip of the lifter bar is defined by the following parameters:
Line 114: Line 121:
In between the point of equilibrium and the lifter bar tip, a media element may roll, slide or be projected into free flight depending on the prevailing forces.
In between the point of equilibrium and the lifter bar tip, a media element may roll, slide or be projected into free flight depending on the prevailing forces.


</hide><div class="user-show">
=== Rolling ===
=== Rolling ===
</div><hide>


If the coefficient of static friction between the lifter and the media element, <math>\mu_{\rm s}</math>, is greater than zero then the element commences movement from the point of equilibrium by pure rolling down the lifter face.
If the coefficient of static friction between the lifter and the media element, <math>\mu_{\rm s}</math>, is greater than zero then the element commences movement from the point of equilibrium by pure rolling down the lifter face.
Line 120: Line 129:
However, if the effects of static friction are ignored, rolling does not occur and the element only experiences sliding motion (see [[Tumbling Mill (Media Trajectory)#Sliding|Sliding]] below).
However, if the effects of static friction are ignored, rolling does not occur and the element only experiences sliding motion (see [[Tumbling Mill (Media Trajectory)#Sliding|Sliding]] below).


==== Pure rolling ====  
</hide><div class="user-show">
==== Pure rolling ====
</div><hide>


The moments of inertia of ball (spherical) and rod (cylindrical) media elements are different, which leads to separate formulations of the equations of motion whilst rolling.
The moments of inertia of ball (spherical) and rod (cylindrical) media elements are different, which leads to separate formulations of the equations of motion whilst rolling.
Line 156: Line 167:
The velocity of the media element may be found by substituting the value of <math>t_{\rm L}</math> obtained into the equation for <math>\dot s</math> under pure rolling. The angle of the lifter bar face when the media element is at the tip of the lifter is similarly <math>\gamma_{\rm L} = \gamma_0 + \Omega t_{\rm L}</math> under pure rolling.
The velocity of the media element may be found by substituting the value of <math>t_{\rm L}</math> obtained into the equation for <math>\dot s</math> under pure rolling. The angle of the lifter bar face when the media element is at the tip of the lifter is similarly <math>\gamma_{\rm L} = \gamma_0 + \Omega t_{\rm L}</math> under pure rolling.


</hide><div class="user-show">
==== Maximum angle for pure rolling ====
==== Maximum angle for pure rolling ====
</div><hide>


During pure rolling and prior to reaching the lifter tip, the frictional force causing angular acceleration of the element may be exceeded by the acting gravitational and centrifugal forces. At this point, the element begins to slip across the lifter face, in addition to continued rolling.
During pure rolling and prior to reaching the lifter tip, the frictional force causing angular acceleration of the element may be exceeded by the acting gravitational and centrifugal forces. At this point, the element begins to slip across the lifter face, in addition to continued rolling.
Line 178: Line 191:
If the angle of the lifter bar face when the media element is at the tip of the lifter after pure rolling , <math>\gamma_{\rm L}</math>, exceeds <math>\gamma_{\rm m(min)}</math> then a transition to combined rolling and sliding is possible. Otherwise, the media element only undergoes pure rolling before being projected into free flight.
If the angle of the lifter bar face when the media element is at the tip of the lifter after pure rolling , <math>\gamma_{\rm L}</math>, exceeds <math>\gamma_{\rm m(min)}</math> then a transition to combined rolling and sliding is possible. Otherwise, the media element only undergoes pure rolling before being projected into free flight.


</hide><div class="user-show">
==== Transition to rolling and sliding ====
==== Transition to rolling and sliding ====
</div><hide>


The time at which a transition from pure rolling to combined rolling and sliding occurs, <math>t_{\rm I}</math> (s), is found by numerically solving for <math>t</math> where the following inequality no longer holds:
The time at which a transition from pure rolling to combined rolling and sliding occurs, <math>t_{\rm I}</math> (s), is found by numerically solving for <math>t</math> where the following inequality no longer holds:
Line 203: Line 218:
The position, <math>s_{\rm I}</math> (m), and velocity, <math>\dot s_{\rm I}</math> (m), of the media element at <math>t_{\rm I}</math> can then be computed using the pure rolling equations for <math>s(t)</math> and <math>\dot s</math> above. The angle of the lifter bar face at <math>t_{\rm I}</math>, <math>\gamma_{\rm I}</math> (rad), is found from <math>\gamma_{\rm I} = \gamma_0 + \Omega t_{\rm I}</math>.
The position, <math>s_{\rm I}</math> (m), and velocity, <math>\dot s_{\rm I}</math> (m), of the media element at <math>t_{\rm I}</math> can then be computed using the pure rolling equations for <math>s(t)</math> and <math>\dot s</math> above. The angle of the lifter bar face at <math>t_{\rm I}</math>, <math>\gamma_{\rm I}</math> (rad), is found from <math>\gamma_{\rm I} = \gamma_0 + \Omega t_{\rm I}</math>.


</hide><div class="user-show">
=== Sliding ===
=== Sliding ===
</div><hide>


</hide><div class="user-show">
==== Sliding after rolling ====
==== Sliding after rolling ====
</div><hide>


If sliding motion commences after rolling, the position and velocity of the element at time <math>\tau</math> are:
If sliding motion commences after rolling, the position and velocity of the element at time <math>\tau</math> are:
Line 219: Line 238:
The total time for the media element to travel from the point of equilibrium to the tip of the lifter bar by rolling and sliding is <math>t_{\rm L} = t_{\rm I} + \tau_{\rm L}</math> (s).
The total time for the media element to travel from the point of equilibrium to the tip of the lifter bar by rolling and sliding is <math>t_{\rm L} = t_{\rm I} + \tau_{\rm L}</math> (s).


</hide><div class="user-show">
==== Pure sliding ====
==== Pure sliding ====
</div><hide>


If the coefficient of static friction (<math>\mu_{\rm s}</math>) is zero, i.e. ignored, rolling does not commence and the media element undergoes sliding directly from the point of equilibrium. The above equations of motion for sliding are subsequently utilised with the following values substituted:
If the coefficient of static friction (<math>\mu_{\rm s}</math>) is zero, i.e. ignored, rolling does not commence and the media element undergoes sliding directly from the point of equilibrium. The above equations of motion for sliding are subsequently utilised with the following values substituted:
Line 229: Line 250:
and <math>t_{\rm L} = \tau_{\rm L}</math>.
and <math>t_{\rm L} = \tau_{\rm L}</math>.


</hide><div class="user-show">
=== Free-flight ===
=== Free-flight ===
</div><hide>


A media element may be projected into free flight in two ways:
A media element may be projected into free flight in two ways:
Line 275: Line 298:
:<math>(v_{x{\rm E}},\, v_{y{\rm E}}) = (v_{x{\rm L}}, \; v_{y{\rm L}} - gt)</math>
:<math>(v_{x{\rm E}},\, v_{y{\rm E}}) = (v_{x{\rm L}}, \; v_{y{\rm L}} - gt)</math>


== Additional notes ==
</hide><div class="user-show">
=== Additional notes ===
</div><hide>


{| style="float:right; margin-left: 20px;"
{| style="float:right; margin-left: 20px;"
Line 282: Line 307:
|}
|}


=== Friction estimates ===
</hide><div class="user-show">
==== Friction estimates ====
</div><hide>


Powell's (1991) experimental work separately investigated the coefficients of static  and kinetic friction between a media element and a lifter bar. The findings suggest:
Powell's (1991) experimental work separately investigated the coefficients of static  and kinetic friction between a media element and a lifter bar. The findings suggest:
Line 292: Line 319:
Adequate estimates of the coefficients of friction for simulation purposes may be 0 or 0.05 for <math>\mu_{\rm s}</math> and 0.19 for <math>\mu_{\rm k}</math>, but is left to user discretion.
Adequate estimates of the coefficients of friction for simulation purposes may be 0 or 0.05 for <math>\mu_{\rm s}</math> and 0.19 for <math>\mu_{\rm k}</math>, but is left to user discretion.


=== Extracting lifter geometry ===
</hide><div class="user-show">
==== Extracting lifter geometry ====
</div><hide>


Modern mill interior laser scanning devices and/or design drawings provide accurate parametric maps of lifter bar geometry, which may be used to quantify the lifter height (<math>h</math>), lifter width (<math>2y</math>) and lifter face angle (<math>\rho</math>) properties for media trajectory simulation.  
Modern mill interior laser scanning devices and/or design drawings provide accurate parametric maps of lifter bar geometry, which may be used to quantify the lifter height (<math>h</math>), lifter width (<math>2y</math>) and lifter face angle (<math>\rho</math>) properties for media trajectory simulation.  
Line 308: Line 337:
<br>
<br>
<br>
<br>
</hide>


== Excel ==
== Excel ==
Line 431: Line 461:
! colspan="3" style="text-align:left;" |''Results''
! colspan="3" style="text-align:left;" |''Results''
|-
|-
| colspan="3" |''Point Of Equilibrium''
| colspan="3" |''PointOfEquilibrium''
|-
|-
| PositionAngle
| PositionAngle / Phi
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
| Angular position of the point of equilibrium.
| Angular position of the point of equilibrium.
|-
|-
| colspan="3" |''Leaves Lifter''
| colspan="3" |''LeavesLifter''
|-
|-
|PositionAngle
|PositionAngle / Phi
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
| Angular position of the point where the media element leaves the lifter.
| Angular position of the point where the media element leaves the lifter.
Line 451: Line 481:
| Cartesian ''y'' coordinate of the point where the media element leaves the lifter.
| Cartesian ''y'' coordinate of the point where the media element leaves the lifter.
|-
|-
|Velocity
|Velocity / V
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
| Velocity of the media element at the point where it leaves the lifter.
| Velocity of the media element at the point where it leaves the lifter.
|-
|-
|VelocityAngle
|VelocityAngle / PhiV
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
| Angular direction of the velocity of the media element at the point where it leaves the lifter.
| Angular direction of the velocity of the media element at the point where it leaves the lifter.
|-
|-
| colspan="3" |''Impacts Shell''
| colspan="3" |''ImpactsShell''
|-
|-
|PositionAngle
|PositionAngle / Phi
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
| Angular position of the point where the media element impacts the mill shell.
| Angular position of the point where the media element impacts the mill shell.
Line 473: Line 503:
| Cartesian ''y'' coordinate of the point where the media element impacts the mill shell.
| Cartesian ''y'' coordinate of the point where the media element impacts the mill shell.
|-
|-
|Velocity
|Velocity / V
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
| Velocity of the media element at the point where it impacts the mill shell.
| Velocity of the media element at the point where it impacts the mill shell.
|-
|-
|VelocityAngle
|VelocityAngle / PhiV
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
| Angular direction of the velocity of the media element at the point where it impacts the mill shell.
| Angular direction of the velocity of the media element at the point where it impacts the mill shell.
|-
|-
| style="vertical-align:top;" |State
| style="vertical-align:top;" |State
|style="background: #eaecf0" style="vertical-align:top;"| Display
|style="vertical-align:top; background:#eaecf0" | Display
| Text description of the motion of the media element. Possible values are:
| Text description of the motion of the media element. Possible values are:
* "Element is projected into free flight from point of equilibrium."
* "Element is projected into free flight from point of equilibrium."
Line 493: Line 523:
|-
|-
! colspan="3" style="text-align:left;" |''Trajectory''
! colspan="3" style="text-align:left;" |''Trajectory''
|-
| ShowTrajectory
| CheckBox
| If enabled, the (x, y) coordinate data of the element trajectory is displayed below.
|-
|-
|TrajectoryData
|TrajectoryData
Line 500: Line 534:
|Point, X, Y
|Point, X, Y
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
| X and Y coordinates of the media element trajectory, from the point of equilibrium to point of impact with the mill shell.
| X and Y coordinates of the media element trajectory, from the point of equilibrium to point of impact with the mill shell. Only visible if ''ShowTrajectory'' is enabled above.
|}
|}


Latest revision as of 07:23, 1 May 2025

Description

Figure 1. Example tumbling mill media trajectory, including Morrell Continuum charge position.

This article describes Powell's (1991) method for predicting the trajectory of the outer media elements in a tumbling mill.[1]

The approach predicts the point of impact of media elements projected into free flight after transit down a lifter bar surface, based on element size, lifter bar geometry, mill diameter and mill rotational speed.

The tumbling mill media trajectory model is particularly useful when combined with an estimate of charge position (e.g. Morrell's method), which allows analyses such as:

  • Identifying and mitigating the risks of shell liner damage from media impact through lifter bar (or mill) design
  • Monitoring trajectory and point of impact changes with charge level, mill speed or liner and lifter bar wear in operational mills
  • Limiting the maximum operating speed (and hence power and throughput) in a mill simulation or process control sub-systems

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Point of equilibrium

Lifter bar tip position

Rolling

Pure rolling

Maximum angle for pure rolling

Transition to rolling and sliding

Sliding

Sliding after rolling

Pure sliding

Free-flight

Additional notes

Friction estimates

Extracting lifter geometry

Excel

The tumbling mill media trajectory model may be invoked from the Excel formula bar with the following function call: 

=mdMillPower_MillMediaTrajectory(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

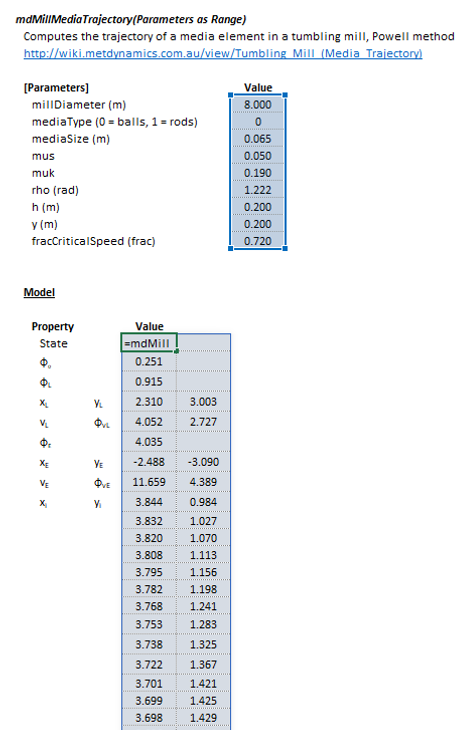
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:


where:

  • is the mill diameter inside liners (m), i.e.
  • is the media element diameter (m), i.e.
  • is the type of media element, balls or rods (0 = Balls, 1 = Rods)
  • is the fraction critical speed of the mill (frac)

and:

  • is a text string that describes the motion of the media element
  • is the number of trajectory points for plotting
Figure 7. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The media trajectory model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
MediaTraj
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
Requirements
MillDiameter Input/Display Diameter of the mill (inside liners).
FracCS Input/Display Fraction critical speed of the mill.
MediaType Ball/Rod Type of media element, balls or rods.
MediaSize Display Diameter of the media element.
mus Input Coefficient of static friction.
muk Input Coefficient of kinematic friction.
rho Input Lifter face angle, angle between the face surface and the base of the lifter bar.
h Input Height of the lifter bar.
2y Input Width of the lifter bar.
Results
PointOfEquilibrium
PositionAngle / Phi Display Angular position of the point of equilibrium.
LeavesLifter
PositionAngle / Phi Display Angular position of the point where the media element leaves the lifter.
X Display Cartesian x coordinate of the point where the media element leaves the lifter.
Y Display Cartesian y coordinate of the point where the media element leaves the lifter.
Velocity / V Display Velocity of the media element at the point where it leaves the lifter.
VelocityAngle / PhiV Display Angular direction of the velocity of the media element at the point where it leaves the lifter.
ImpactsShell
PositionAngle / Phi Display Angular position of the point where the media element impacts the mill shell.
X Display Cartesian x coordinate of the point where the media element impacts the mill shell.
Y Display Cartesian y coordinate of the point where the media element impacts the mill shell.
Velocity / V Display Velocity of the media element at the point where it impacts the mill shell.
VelocityAngle / PhiV Display Angular direction of the velocity of the media element at the point where it impacts the mill shell.
State Display Text description of the motion of the media element. Possible values are:
  • "Element is projected into free flight from point of equilibrium."
  • "Element slides to end of the lifter and is then projected into free flight."
  • "Element slides and is projected into free flight before the end of the lifter."
  • "Element rolls to the end of the lifter and is projected into free flight."
  • "Element rolls then slides to the end of the lifter before being projected into free flight."
  • "Element rolls then slides and is projected into free flight before the end of the lifter."
  • "Element rolls and is projected into free flight before the end of the lifter."
Trajectory
ShowTrajectory CheckBox If enabled, the (x, y) coordinate data of the element trajectory is displayed below.
TrajectoryData ButtonCopyToClipboard.png Copies the full set of trajectory coordinates to the Windows clipboard in CSV format.
Point, X, Y Display X and Y coordinates of the media element trajectory, from the point of equilibrium to point of impact with the mill shell. Only visible if ShowTrajectory is enabled above.

See also

References

  1. ↑ Powell, M.S., 1991. The effect of liner design on the motion of the outer grinding elements in a rotary mill. International Journal of Mineral Processing, 31(3-4), pp.163-193.
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Tumbling_Mill_(Media_Trajectory)&oldid=2515"