Tumbling Mill (Power, Morrell Discrete Shell): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
m (1 revision imported)
imported>Scott.Munro
mNo edit summary
 
(4 intermediate revisions by 3 users not shown)
Line 8: Line 8:
== Model theory ==
== Model theory ==


{{Restricted content}}
<hide>
[[File:TumblingMillPower5.png|thumb|700px|thumb|Figure 1. Grate discharge tumbling mill profile illustrating the Morrell D model's charge shape and concentric shell layers (at increments of five for clarity).<br><br>The radial position (<math>r</math>), shoulder position (<math>\theta_{S25}</math>) and toe position (<math>\theta_{T25}</math>) of shell 25 are shown as an example.]]
[[File:TumblingMillPower5.png|thumb|700px|thumb|Figure 1. Grate discharge tumbling mill profile illustrating the Morrell D model's charge shape and concentric shell layers (at increments of five for clarity).<br><br>The radial position (<math>r</math>), shoulder position (<math>\theta_{S25}</math>) and toe position (<math>\theta_{T25}</math>) of shell 25 are shown as an example.]]


Line 24: Line 27:
where <math>P_{\rm r}</math> is the power draw of discrete shell <math>i</math>, and <math>n</math> is the number of shells comprising the charge.
where <math>P_{\rm r}</math> is the power draw of discrete shell <math>i</math>, and <math>n</math> is the number of shells comprising the charge.


</hide><div class="user-show">
=== Power per shell ===
=== Power per shell ===
</div><hide>


The power draw of an individual shell in the cylindrical section of the mill due to the potential energy of the charge, the kinetic energy of the charge and the potential energy of the slurry pool is:
The power draw of an individual shell in the cylindrical section of the mill due to the potential energy of the charge, the kinetic energy of the charge and the potential energy of the slurry pool is:
Line 49: Line 54:
and all angles are unit circle positive.
and all angles are unit circle positive.


</hide><div class="user-show">
=== Shell rotational rate ===
=== Shell rotational rate ===
</div><hide>


Shells are assumed to slip against one another and progressively lose rotational speed as the radial position moves from the top of the lifters towards the centre of rotation.
Shells are assumed to slip against one another and progressively lose rotational speed as the radial position moves from the top of the lifters towards the centre of rotation.
Line 67: Line 74:
Shells located between the top of the lifters and outer mill shell are locked into place by the lifters, and rotate at the mill rotational speed without loss.
Shells located between the top of the lifters and outer mill shell are locked into place by the lifters, and rotate at the mill rotational speed without loss.


</hide><div class="user-show">
=== Characteristic media size ===
=== Characteristic media size ===
</div><hide>


The thickness of each shell, <math>\bar x</math>, is related to the particle size distribution of the charge (balls and coarse rocks). Morrell adopted the concept of a ''characteristic media size'' to determine a representative layer thickness.
The thickness of each shell, <math>\bar x</math>, is related to the particle size distribution of the charge (balls and coarse rocks). Morrell adopted the concept of a ''characteristic media size'' to determine a representative layer thickness.
Line 98: Line 107:
Calculation of the characteristic media size requires the full particle size distribution of balls and ore in the mill.
Calculation of the characteristic media size requires the full particle size distribution of balls and ore in the mill.


For ball mills, the characteristic media size may be estimated by neglecting ore particles and assuming the ball size size distribution is in an equilibrium state (ball make-up rate = ball ejection rate), in which case:
For ball mills, the characteristic media size may be estimated by neglecting ore particles and assuming the ball size distribution is in an equilibrium state (ball make-up rate = ball ejection rate), in which case:


:<math>\bar x = 0.5559 D_{\rm B}</math>
:<math>\bar x = 0.5559 D_{\rm B}</math>
Line 106: Line 115:
Note that Morrell's ball size equilibrium assumptions are also consistent with the tumbling mill media string approach described [[Tumbling Mill (Media Strings)|here]].
Note that Morrell's ball size equilibrium assumptions are also consistent with the tumbling mill media string approach described [[Tumbling Mill (Media Strings)|here]].


</hide><div class="user-show">
=== Charge position ===
=== Charge position ===
</div><hide>


Morrell developed the following series of relations to estimate the geometry of a shell at radial position <math>r</math>.
Morrell developed the following series of relations to estimate the geometry of a shell at radial position <math>r</math>.


</hide><div class="user-show">
==== Toe and shoulder positions ====
==== Toe and shoulder positions ====
</div><hide>


The position of the '''toe''' of a shell, <math>\theta_{{\rm T}r}</math> (rad), is defined as:  
The position of the '''toe''' of a shell, <math>\theta_{{\rm T}r}</math> (rad), is defined as:  
Line 137: Line 150:
The remaining shells at radial distances above the height of the lifters use Morrell's original shoulder and toe position relations described above.
The remaining shells at radial distances above the height of the lifters use Morrell's original shoulder and toe position relations described above.


</hide><div class="user-show">
==== Slurry pool position ====
==== Slurry pool position ====
</div><hide>


The position of the '''slurry pool''' level, <math>\theta_{\rm TO}</math> (rad), was assumed to be equal to the charge toe, <math>\theta_{\rm T}</math>, for grate mills. For overflow mills, a value of 3.395 radians was calculated where the trunnion radius, <math>r_{\rm t}</math>, is one quarter (0.25) of the mill radius, <math>r_{\rm m}</math>.
The position of the '''slurry pool''' level, <math>\theta_{\rm TO}</math> (rad), was assumed to be equal to the charge toe, <math>\theta_{\rm T}</math>, for grate mills. For overflow mills, a value of 3.395 radians was calculated where the trunnion radius, <math>r_{\rm t}</math>, is one quarter (0.25) of the mill radius, <math>r_{\rm m}</math>.


This implementation of the Discrete Shell model improves estimation of the slurry pool position for overflow mills by adopting the approach described by Morrell (2016) and corrected by Shi (2016):{{Morrell_(2016)}}{{Shi_(2016)}}
This implementation of the Discrete Shell model improves estimation of the slurry pool position for overflow mills by adopting the approach described by Morrell (2016) and typographically corrected by Shi (2016):{{Morrell_(2016)}}{{Shi_(2016)}}


:<math>\theta_{\rm TO} = \arcsin \left ( \frac{r_{\rm t} - h}{r_{\rm m}} \right )</math>
:<math>\theta_{\rm TO} = \arcsin \left ( \frac{r_{\rm t} - h}{r_{\rm m}} \right )</math>
Line 151: Line 166:
and <math>Q</math> is the volumetric flow rate of pulp to/from the overflow mill.
and <math>Q</math> is the volumetric flow rate of pulp to/from the overflow mill.


</hide><div class="user-show">
==== Shell volume ====
==== Shell volume ====
</div><hide>


The shell shoulder and toe positions only account for the active portion of the charge, i.e. the fraction not in free-flight between the should and the toe. The total volume of a shell, including the inactive portion, must be computed by the model algorithm to ensure the sum of all shell volumes equals the total charge volume. The total shell volume is therefore:
The shell shoulder and toe positions only account for the active portion of the charge, i.e. the fraction not in free-flight between the should and the toe. The total volume of a shell, including the inactive portion, must be computed by the model algorithm to ensure the sum of all shell volumes equals the total charge volume. The total shell volume is therefore:
Line 167: Line 184:
:<math>t_{{\rm f}r} = 2r \left( \frac{\sin \theta_{{\rm S}r} - \sin \theta_{{\rm T}r}}{g} \right )^{0.5}</math>
:<math>t_{{\rm f}r} = 2r \left( \frac{\sin \theta_{{\rm S}r} - \sin \theta_{{\rm T}r}}{g} \right )^{0.5}</math>


</hide><div class="user-show">
=== Charge density ===
=== Charge density ===
</div><hide>


Morrell's 1993 Discrete Shell model algorithm assumed the grinding media interstices were completely filled with slurry.  
Morrell's 1993 Discrete Shell model algorithm assumed the grinding media interstices were completely filled with slurry.  
Line 182: Line 201:
* <math>J_{\rm B}</math> is the volumetric fraction of the mill occupied by balls (including voids) (v/v)
* <math>J_{\rm B}</math> is the volumetric fraction of the mill occupied by balls (including voids) (v/v)


</hide><div class="user-show">
=== Conical ends ===
=== Conical ends ===
</div><hide>


[[File:TumblingMillPower6.png|thumb|450px|Figure 3. Discretisation of cone end shells, Morrell Discrete Shell tumbling mill power model (after Morrell, 1993).{{Morrell_(1993)}}]]
[[File:TumblingMillPower6.png|thumb|450px|Figure 3. Discretisation of cone end shells, Morrell Discrete Shell tumbling mill power model (after Morrell, 1993).{{Morrell_(1993)}}]]
Line 192: Line 213:
Power in the cone slices is subsequently calculated using the same approach as the shells in the cylindrical section of the mill.
Power in the cone slices is subsequently calculated using the same approach as the shells in the cylindrical section of the mill.


</hide><div class="user-show">
=== No-load power ===
=== No-load power ===
</div><hide>


This implementation of the Discrete Shell model uses Morrell's 1996 term for no-load power:{{Morrell (1996a)}}
This implementation of the Discrete Shell model uses Morrell's 1996 term for no-load power:{{Morrell (1996a)}}
Line 206: Line 229:
where <math>\alpha_{c}</math> is the cone angle, measured as the angular displacement of the cone surface from the vertical direction.
where <math>\alpha_{c}</math> is the cone angle, measured as the angular displacement of the cone surface from the vertical direction.


</hide><div class="user-show">
=== Model algorithm ===
=== Model algorithm ===
</div><hide>


The Morrell D model adopts the algorithm outlined below to compute total mill power draw:
The Morrell D model adopts the algorithm outlined below to compute total mill power draw:
Line 215: Line 240:
# An inner loop around steps 1 - 2 also makes incremental adjustments to the characteristic media size value, <math>\bar x</math>, to minimise the numerical error associated with discretising the real number-valued charge volume into an integer number of shells with variable volume.
# An inner loop around steps 1 - 2 also makes incremental adjustments to the characteristic media size value, <math>\bar x</math>, to minimise the numerical error associated with discretising the real number-valued charge volume into an integer number of shells with variable volume.
# Net power draw is calculated by summing the shell power values.
# Net power draw is calculated by summing the shell power values.
# The net power calculation process in steps 1 - 5 is conducted twice; once with the laboratory-observed slip parameter (<math>\gamma</math>) value of 0.02433, and then again with the industrial mill value of 0.0028 (or a user-specified value). This estimates the fractions of net power draw attributable to to ''attrition/abrasion'' (industrial mill only) and ''impact'' mechanisms (industrial and laboratory mills).
# The net power calculation process in steps 1 - 5 is conducted twice; once with the laboratory-observed slip parameter (<math>\gamma</math>) value of 0.02433, and then again with the industrial mill value of 0.0028 (or a user-specified value). This estimates the fractions of net power draw attributable to ''attrition/abrasion'' (industrial mill only) and ''impact'' mechanisms (industrial and laboratory mills).
# Total power draw is finally calculated by adding the net power and no-load power values.
# Total power draw is finally calculated by adding the net power and no-load power values.


== Additional notes ==
</hide><div class="user-show">
=== Additional notes ===
</div><hide>


The Morrell D model requires an estimation of the charge particle size distribution (balls and coarse ore), and lifter geometry, both of which are typically not available during normal mill operation. In addition, the model applies a a multi-step, looping computational algorithm which makes it unsuited to spreadsheet-style calculations. For these reasons, the Morrell D model has not been tested and applied as extensively as the Morrell Continuum and Empirical models.
The Morrell D model requires an estimation of the charge particle size distribution (balls and coarse ore), and lifter geometry, both of which are typically not available during normal mill operation. In addition, the model applies a multi-step, looping computational algorithm which makes it unsuited to spreadsheet-style calculations. For these reasons, the Morrell D model has not been tested and applied as extensively as the Morrell Continuum and Empirical models.


Nevertheless, the Morrell D model may find utility when coupled with process models that predict mill load and ball particle size distributions (e.g. [[AG/SAG Mill (Mutambo)]] and [[Tumbling Mill (Media Strings)]]), and lifter wear measurements from modern laser scanning devices.
Nevertheless, the Morrell D model may find utility when coupled with process models that predict mill load and ball particle size distributions (e.g. [[AG/SAG Mill (Variable Rates)]] and [[Tumbling Mill (Media Strings)]]), and lifter wear measurements from modern laser scanning devices.


Like the Continuum and Empirical models, the Morrell D model is only valid for grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>. The slurry pool present in overflow discharge mills is included within the model formulation via the <math>\theta_{\rm TO}</math> term, as described above.
Like the Continuum and Empirical models, the Morrell D model is only valid for grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>. The slurry pool present in overflow discharge mills is included within the model formulation via the <math>\theta_{\rm TO}</math> term, as described above.
</hide>


== Excel ==
== Excel ==

Latest revision as of 08:17, 1 May 2025

Description

This article describes the Morrell Discrete Shell (Morrell D) method for estimating the power draw of a tumbling mill.[1] The Morrel D model adopts a more sophisticated treatment of charge dynamics than the Morrell Continuum method:

  • The total charge is subdivided into discrete layers, or shells, whose size and position may individually vary due to grinding media size, mill speed, lift bar geometry and other conditions.
  • The rate at which potential and kinetic energy is imparted to each shell during mill rotation is calculated separately and subsequently summed to estimate the total mill power draw.

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Power per shell

Shell rotational rate

Characteristic media size

Charge position

Toe and shoulder positions

Slurry pool position

Shell volume

Charge density

Conical ends

No-load power

Model algorithm

Additional notes

Excel

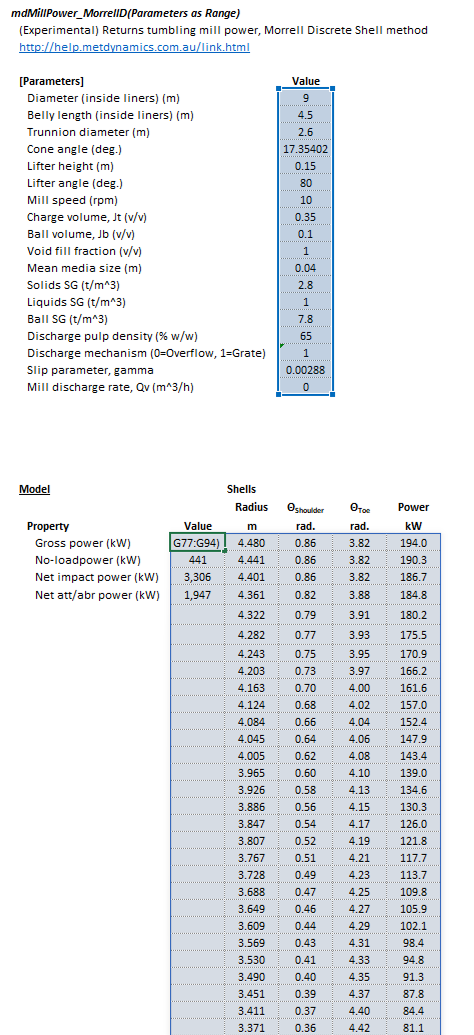
The Morrell Discrete Shell mill power model may be invoked from the Excel formula bar with the following function call: 

=mdMillPower_MorrellD(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:


where:

  • is the diameter of the discharge trunnion (m), i.e.
  • is the lifter height (m)
  • is the lifter face angle (deg.)
  • is the rotational speed of the mill (rpm)
  • is the density of liquids (t/m3)
  • is the mass fraction of solids in the discharge pulp (% w/w)
  • is the discharge configuration type, 0 = Grate, 1 = Overflow
  • is the volumetric discharge flow rate of pulp from the mill (m3/h)
  • is the power draw attributable to the impact mechanism (kW)
  • is the power draw attributable to the attrition/abrasion mechanisms (kW)
  • is the number of discrete shells
  • is the radius of shell (m)
  • is the angular position of the shoulder of shell (rad)
  • is the angular position of the toe of shell (rad)
  • is the power drawn by shell (kW)
Figure 4. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Morrell Discrete Shell power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
MorrellC
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
MillDiameter Input/Display Diameter of the mill (inside liners).
BellyLength Input/Display Length of the cylindrical section (belly) of the mill (inside liners).
TrunnionDiameter Input/Display Diameter of the trunnion (inside liners).
ConeAngle Input/Display Angular displacement of the cone surface from the vertical direction.
LifterHeight Input Height of the lifters above the liner surface
LifterAngle Input Angle between the face and the base of the lifter
MillRPM Input/Display Mill rotational speed
Jt Input/Display Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
BallLoadVol Input/Display Volumetric fraction of the mill occupied by balls (including voids).
VoidFillFraction Input/Display Volumetric fraction of interstitial grinding media voidage occupied by slurry.
MeanMediaSize Input Characteristic media size,
SolidsSG Display Specific Gravity or density of solids.
LiquidsSG Display Specific Gravity or density of liquids.
BallSG Input/Display Specific Gravity or density of balls.
Cw Display Mass fraction of solids in discharge slurry.
DischargeType Grate/Overflow Discharge configuration, grate or overflow.
Gamma Input Value of the slip coefficient,
ThetaShoulder Display Angle of the shoulder of the outermost charge shell.
ThetaToe Display Angle of the toe of the outermost charge toe
NoLoadPower Display Power input to the motor when the mill is empty (no balls, rocks or slurry).
NetImpactPower Display Net power attributable to impact
NetAttAbrPower Display Net power attributable to attrition/abrasion
NetPower Display Charge motion power.
GrossPower Display Power input to the motor.

See also

References

  1. ↑ Morrell, S., 1993. The prediction of power draw in wet tumbling mills (Doctoral dissertation, University of Queensland).
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Tumbling_Mill_(Power,_Morrell_Discrete_Shell)&oldid=2469"