Hydrocyclone (Narasimha-Mainza): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
imported>Scott.Munro
mNo edit summary
 
(16 intermediate revisions by 3 users not shown)
Line 7: Line 7:
* A slurry viscosity term that includes the effects of very fine particles
* A slurry viscosity term that includes the effects of very fine particles
* Terms for cyclone inclination, particle density, g-forces, flow regime (Reynolds Number) and turbulent diffusion
* Terms for cyclone inclination, particle density, g-forces, flow regime (Reynolds Number) and turbulent diffusion
Narasimha et al. (2014b) subsequently presented a ''multi-component'' version of the same model, with revised equations for cut size and sharpness of separation per ore component:{{Narasimha et al. (2014b)}}


== Model theory ==
== Model theory ==


{{Restricted content}}
<hide>
[[File:HydrocycloneNarasimhaMainza1.png|thumb|375px|Figure 1. The dimensions of a hydrocyclone required by the Narasimha-Mainza model.]]
[[File:HydrocycloneNarasimhaMainza1.png|thumb|375px|Figure 1. The dimensions of a hydrocyclone required by the Narasimha-Mainza model.]]


The Narasima-Mainza model comprises an equation for the efficiency curve (partition to overflow) and several sub-equations that describe its parameters:
The Narasimha-Mainza model comprises an equation for the efficiency curve (partition to overflow) and several sub-equations that describe its parameters:
* the corrected cut size
* the corrected cut size
* the sharpness of separation
* the sharpness of separation
Line 19: Line 24:
In addition, a relationship between throughput and operating pressure is presented.
In addition, a relationship between throughput and operating pressure is presented.


</hide><div class="user-show">
=== Efficiency curve ===
=== Efficiency curve ===
</div><hide>


The Narasimha-Mainza model applies the [[Partitions|Whiten-Beta efficiency curve]] to partition particles to the overflow stream:
The Narasimha-Mainza model applies the [[Partition (Size, Whiten-Beta)|Whiten-Beta efficiency curve]] to partition particles to the overflow stream:


{{Model theory (Text, Whiten-Beta Efficiency Curve)}}
{{Model theory (Text, Whiten-Beta Efficiency Curve)}}


</hide><div class="user-show">
=== Corrected cut size ===
=== Corrected cut size ===
</div><hide>


The corrected cut size, <math>d_{50c}</math> (m), is computed from:
The corrected cut size, <math>d_{\rm 50c}</math> (m), is computed from:


:<math>
:<math>
\dfrac {d_{50c}}{D_c} = K_{d0} {\left( \dfrac {D_o} {D_c} \right)}^{1.093} {\left( \dfrac {D_u} {D_c} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_i} {D_c} \right)}^{-0.936} {\left( \dfrac {L_c} {D_c} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_s - \rho_f}{\rho_f} \right)}^{-0.217}
\dfrac {d_{\rm 50c}}{D_{\rm c}} = K_{\rm d0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{1.093} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.936} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{-0.217}
</math>
</math>


where:
where:
* <math>K_{d0}</math> is a calibration factor which should be fitted to operating data
* <math>K_{\rm d0}</math> is a calibration factor which should be fitted to operating data
* <math>D_c</math> is diameter of the cyclone (m)
* <math>D_{\rm c}</math> is diameter of the cyclone (m)
* <math>D_i</math> is diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet (m)
* <math>D_{\rm i}</math> is diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet (m)
* <math>D_o</math> is diameter of the vortex finder (overflow) (m)
* <math>D_{\rm o}</math> is diameter of the vortex finder (overflow) (m)
* <math>D_u</math> is diameter of the apex/spigot (underflow) (m)
* <math>D_{\rm u}</math> is diameter of the apex/spigot (underflow) (m)
* <math>L_c</math> is length of the cylindrical section (m)
* <math>L_{\rm c}</math> is length of the cylindrical section (m)
* <math>\theta</math> is the cone full angle (deg.)
* <math>\theta</math> is the cone full angle (deg.)
* <math>i</math> is the angle of inclination from the vertical (rad)
* <math>i</math> is the angle of inclination from the vertical (rad)
* <math>f_v</math> is the volume fraction of solids in the feed (v/v)
* <math>f_{\rm v}</math> is the volume fraction of solids in the feed (v/v)
* <math>\rho_s</math> is the density of solids in the feed (t/m<sup>3</sup>)
* <math>\rho_{\rm s}</math> is the density of solids in the feed (t/m<sup>3</sup>)
* <math>\rho_f</math> is the density of the fluid (liquids) in the feed (t/m<sup>3</sup>)
* <math>\rho_{\rm f}</math> is the density of the fluid (liquids) in the feed (t/m<sup>3</sup>)
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>)
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>)


The Reynolds Number, <math>Re</math>, is:
The Reynolds Number, <math>\rm Re</math>, is:


:<math>Re  = \dfrac{1000 V_i D_c \rho_p}{0.001\mu_r}</math>
:<math>{\rm Re} = \dfrac{1000 V_i D_{\rm c} \rho_{\rm p}}{0.001\mu_{\rm r}}</math>


The feed inlet velocity, <math>V_i</math> (m/s), is:
The feed inlet velocity, <math>V_i</math> (m/s), is:


:<math>V_i = \dfrac{Q_f}{\dfrac{\pi}{4}{D_i}^2}</math>
:<math>V_i = \dfrac{Q_{\rm f}}{\dfrac{\pi}{4}{D_{\rm i}}^2}</math>


where <math>Q_f</math> is the volumetric feed flow rate (m<sup>3</sup>/h), and <math>\rho_p</math> is the density of the feed pulp (t/m<sup>3</sup>).
where <math>Q_{\rm f}</math> is the volumetric feed flow rate (m<sup>3</sup>/h), and <math>\rho_{\rm p}</math> is the density of the feed pulp (t/m<sup>3</sup>).


The relative slurry viscosity, <math>\mu_r</math>, is the ratio of slurry and water viscosities, <math>\mu_m</math> and <math>\mu_w</math>, which is approximated by:
The relative slurry viscosity, <math>\mu_{\rm r}</math>, is the ratio of slurry and water viscosities, <math>\mu_{\rm m}</math> and <math>\mu_{\rm w}</math>, which is approximated by:


:<math>\mu_r = \dfrac{\mu_m}{\mu_w} = \left ( 1 - \dfrac{f_v}{0.622} \right)^{-1.55} ({F_{-38\mu}})^{0.39}</math>
:<math>\mu_{\rm r} = \dfrac{\mu_{\rm m}}{\mu_{\rm w}} = \left ( 1 - \dfrac{f_{\rm v}}{0.622} \right)^{-1.55} ({F_{-38\mu}})^{0.39}</math>


where <math>F_{-38\mu}</math> is the cumulative fraction passing 38 μm in the feed (frac).
where <math>F_{-38\mu}</math> is the cumulative fraction passing 38 μm in the feed (frac).


</hide><div class="user-show">
=== Liquids recovery ===
=== Liquids recovery ===
</div><hide>


The fraction of feed liquid recovered to the underflow stream, <math>R_f</math>, is related to <math>C</math> (i.e. <math>C = 1 - R_f</math>), and is computed as:
The fraction of feed liquid recovered to the underflow stream, <math>R_{\rm f}</math>, is related to <math>C</math> (i.e. <math>C = 1 - R_{\rm f}</math>), and is computed as:


:<math>
:<math>
R_f = K_{w0} {\left( \dfrac {D_o} {D_c} \right)}^{-1.06787} {\left( \dfrac {D_u} {D_c} \right)}^{2.2062} {\left( \dfrac {V^2_t} {R_{max}g} \right)}^{-0.20472} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{-0.829} {\mu_r}^{-0.7118} {\left( \dfrac {L_c} {D_c} \right)}^{2.424} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.8843} {\left( \dfrac {\rho_s - \rho_f} {\rho_f} \right)}^{0.523} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.793}
R_{\rm f} = K_{\rm w0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{-1.06787} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{2.2062} {\left( \dfrac {V^2_t} {R_{\rm max}g} \right)}^{-0.20472} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{-0.829} {\mu_{\rm r}}^{-0.7118} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{2.424} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.8843} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}} {\rho_{\rm f}} \right)}^{0.523} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.793}
</math>
</math>


where <math>K_{w0}</math> is a calibration factor which should be fitted to operating data.
where <math>K_{\rm w0}</math> is a calibration factor which should be fitted to operating data.


<math>R_{max}</math> is the radius of the cyclone (m), i.e.:
<math>R_{\rm max}</math> is the radius of the cyclone (m), i.e.:


:<math>R_{max} = 0.5 D_c</math>
:<math>R_{\rm max} = 0.5 D_{\rm c}</math>


and the tangential velocity, <math>V_t</math> (m/s), is:
and the tangential velocity, <math>V_{\rm t}</math> (m/s), is:


:<math>V_t = 4.5 V_i \left ( \dfrac{D_i}{D_c} \right )^{1.13}</math>
:<math>V_{\rm t} = 4.5 V_i \left ( \dfrac{D_{\rm i}}{D_{\rm c}} \right )^{1.13}</math>


</hide><div class="user-show">
=== Sharpness of separation ===
=== Sharpness of separation ===
</div><hide>


The sharpness of separation parameter, <math>\alpha</math>, is:
The sharpness of separation parameter, <math>\alpha</math>, is:


:<math>
:<math>
\alpha = K_\alpha {{ {{\left( \dfrac {D_o} {D_c} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_t^2} {gR_{max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_v}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_u} {D_c} \right)}^{-0.567} {\left( \dfrac {\left( \rho_s - \rho_p \right)} {\rho_s} \right)}^{-1.837} {\mu_r}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_c} {D_c} \right)}^{-0.2}} }}
\alpha = K_\alpha {{ {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.567} {\left( \dfrac {\left( \rho_{\rm s} - \rho_{\rm p} \right)} {\rho_{\rm s}} \right)}^{-1.837} {\mu_{\rm r}}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.2}} }}
</math>
</math>


where <math>K_{\alpha}</math> is a calibration factor which should be fitted to operating data.
where <math>K_{\alpha}</math> is a calibration factor which should be fitted to operating data.


</hide><div class="user-show">
=== Cyclone capacity ===
=== Cyclone capacity ===
</div><hide>


The volumetric capacity of a cyclone at a given operating pressure, <math>Q</math> (m<sup>3</sup>/h), is estimated from the pressure-throughput relationship:
The '''volumetric capacity''' of a cyclone at a given operating pressure, <math>Q</math> (m<sup>3</sup>/h), is estimated from the pressure-throughput relationship:


:<math>
:<math>
Q = K_{Q0} {\left( \dfrac {D_i} {D_c} \right)}^{0.45} {D_c}^{2} \sqrt \dfrac P {\rho_p} {\left( \dfrac {D_o} {d_c} \right)}^{1.099} {\left( \dfrac {D_u} {D_c} \right)}^{0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_c} {D_c} \right)}^{0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.092}
Q = K_{\rm Q0} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{0.45} {D_{\rm c}}^{2} \sqrt \dfrac P {\rho_{\rm p}} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{1.099} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.092}
</math>
</math>


where <math>K_{Q0}</math> is a calibration factor which should be fitted to operating data, and <math>P</math> is the pressure drop across the operating cyclone (kPa).
where <math>K_{\rm Q0}</math> is a calibration factor which should be fitted to operating data, and <math>P</math> is the pressure drop across the operating cyclone (kPa).


This expression may be used to estimate the number of cyclones required to accept a given total cluster feed flow rate at a fixed pressure, e.g. a process set point.
This expression may be used to estimate the number of cyclones required to accept a given total cluster feed flow rate at a fixed pressure, e.g. a process set point.


Alternatively, the pressure drop arising from a given feed flow rate may be calculated by rearranging the above equation:
Alternatively, the '''pressure drop''' arising from a given feed flow rate may be calculated by rearranging the above equation:


:<math>
:<math>
P = \rho_p \left [ Q {{K_{Q0}}^{-1} {\left( \dfrac {D_i} {D_c} \right)}^{-0.45} {D_c}^{-2} {\left( \dfrac {D_o} {d_c} \right)}^{-1.099} {\left( \dfrac {D_u} {D_c} \right)}^{-0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_c} {D_c} \right)}^{-0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.092}} \right ]^2
P = \rho_{\rm p} \left [ Q {{K_{\rm Q0}}^{-1} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.45} {D_{\rm c}}^{-2} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{-1.099} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.092}} \right ]^2
</math>
</math>


</hide><div class="user-show">
=== Multi-component modelling ===
=== Multi-component modelling ===
</div><hide>
</hide><div class="user-show">
==== Narasimha, Mainza and Holtham (2014) ====
</div><hide>


The Narasimha-Mainza model formulation only considers the classification of solid particles with a single average feed density, <math>\rho_s</math>.
The Narasimha-Mainza model formulation only considers the classification of solid particles with a single average feed density, <math>\rho_{\rm s}</math>.


Narasimha et al. (2014b) explored the classification of multi-component feeds, deriving modified equations for cut size and sharpness of separation per ore component:{{Narasimha et al. (2014b)}}
Narasimha et al. (2014b) explored the classification of ''multi-component'' feeds, deriving modified equations for cut size and sharpness of separation per ore component:{{Narasimha et al. (2014b)}}


:<math>
:<math>
\dfrac {(d_{50c})_j}{D_c} = K_{d0} {\left( \dfrac {D_o} {D_c} \right)}^{1.093} {\left( \dfrac {D_u} {D_c} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_i} {D_c} \right)}^{-0.936} {\left( \dfrac {L_c} {D_c} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_{sj} - \rho_f}{\rho_f} \right)}^{-1.37}
\dfrac {(d_{\rm 50c})_j}{D_{\rm c}} = K_{\rm d0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{1.093} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.936} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_{{\rm s}j} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{-1.37}
</math>
</math>


Line 122: Line 143:


:<math>
:<math>
\alpha_j = K_\alpha {{ {{\left( \dfrac {D_o} {D_c} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_t^2} {gR_{max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_v}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_u} {D_c} \right)}^{-0.567} {\left(  \rho_{sj} - \rho_p   \right)}^{-0.983} {\mu_r}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_c} {D_c} \right)}^{-0.2}} }}
\alpha_j = K_\alpha {{ {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.567} {\left(  \rho_{{\rm s}j} - \rho_{\rm p}   \right)}^{-0.983} {\mu_{\rm r}}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.2}} }}
</math>
</math>


where <math>\rho_{sj}</math> is the density of solid ore component <math>j</math> (t/m<sup>3</sup>).
where <math>\rho_{{\rm s}j}</math> is the density of solid ore component <math>j</math> (t/m<sup>3</sup>).


A ''multi-component'' version of the Narasimha-Mainza model is available which replaces the average density cut size and sharpness of separation equations with their per ore equivalents above. The multi-component version is named as '''Narasimha-Mainza (Multi)''' to distinguish it from the primary Narasimha-Mainza (2014) formulation.
A multi-component version of the Narasimha-Mainza model is available which replaces the average density cut size and sharpness of separation equations with their per ore equivalents above. The multi-component version is named as '''Narasimha-Mainza (Multi)''' to distinguish it from the primary Narasimha-Mainza (2014) formulation.


</hide><div class="user-show">
==== Silveira, Delboni and Bergerman (2024) ====
</div><hide>
More recently, Silveira et al. (2024) simulated multicomponent classification with the Narasimha-Mainza model by assigning separate cut size and sharpness coefficients to the valuable mineral phase and overall ore partitions.{{Silveira et al. (2024)}}
This concept is extended here to allow the specification of cut size and sharpness coefficients for each ore/mineral/class type in the feed, i.e. <math>(K_{\rm d0})_j</math> and <math>(K_{\alpha 0})_j</math> replacing <math>K_{\rm d0}</math> and <math>K_{\alpha 0}</math>.
</hide><div class="user-show">
=== Partition metrics ===
=== Partition metrics ===
</div><hide>


{{Model theory (Text, Hydrocyclone, Partition Metrics)}}
{{Model theory (Text, Hydrocyclone, Partition Metrics)}}


</hide><div class="user-show">
=== Roping ===
=== Roping ===
</div><hide>


{{Model theory (Text, Hydrocyclone, Roping)}}
{{Model theory (Text, Hydrocyclone, Roping)}}
</hide>


== Additional notes ==
== Additional notes ==


Note that the equations presented by Narasimhsa et al. (2014) differ from those presented in Narasimha's original dissertation.{{Narasimha (2009)}}  
Note that the equations presented by Narasimha et al. (2014) differ from those presented in Narasimha's original dissertation.{{Narasimha (2009)}}  


The user should be aware of which model formulation is being applied when adopting calibration parameters from external sources. Recalibration of model parameters via the Excel interface below is recommended in such cases.
The user should be aware of which model formulation is being applied when adopting calibration parameters from external sources. Recalibration of model parameters via the Excel interface below is recommended in such cases.
Line 147: Line 181:
The Narasimha-Mainza hydrocyclone model may be invoked from the Excel formula bar with the following function call:
The Narasimha-Mainza hydrocyclone model may be invoked from the Excel formula bar with the following function call:


<syntaxhighlight lang="vb">=mdUnit_Hydrocyclone_NarasimhaMainza(Parameters as Range, Size as Range, Feed as Range, OreSG Range)</syntaxhighlight>
<syntaxhighlight lang="vb">=mdUnit_Hydrocyclone_NarasimhaMainza(Parameters as Range, Size as Range, Feed as Range, OreSG Range, Optional Kd0 as Range, Optional Kalpha0 as Range)</syntaxhighlight>


{{Excel (Text, Help, No Arguments)}}
{{Excel (Text, Help, No Arguments)}}
Line 155: Line 189:
{{Excel (Text, Inputs)}}
{{Excel (Text, Inputs)}}


:<math>Parameters=
:<math>\mathit{Parameters}=
\begin{bmatrix}
\begin{bmatrix}
\text{Method}\\
\text{Method}\\
\text{Pressure control}\\
\text{Pressure control}\\
\text{Number of cyclones}\\
\text{Number of cyclones}\\
D_c\text{ (m)}\\
D_{\rm c}\text{ (m)}\\
D_i\text{ (m)}\\
D_{\rm i}\text{ (m)}\\
D_o\text{ (m)}\\
D_{\rm o}\text{ (m)}\\
D_u\text{ (m)}\\
D_{\rm u}\text{ (m)}\\
L_c\text{ (m)}\\
L_{\rm c}\text{ (m)}\\
\theta\text{ (deg.)}\\
\theta\text{ (deg.)}\\
i\text{ (deg.)}\\
i\text{ (deg.)}\\
P\text{ (kPa)}\\
P\text{ (kPa)}\\
K_{d0}\\
K_{\rm d0}\\
K_{Q0}\\
K_{\rm Q0}\\
K_{w0}\\
K_{\rm w0}\\
K_{\alpha}\\
K_{\alpha}\\
\beta\\
\beta\\
(Q_{M,F})_{Liquids}\text{ (t/h)}\\
(Q_{\rm M,F})_{\rm L}\text{ (t/h)}\\
\rho_f\text{ (t/m}^{\text{3}}\text{)}\\
\rho_{\rm f}\text{ (t/m}^{\text{3}}\text{)}\\
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\quad
 
\begin{array}{l}


Size = \begin{bmatrix}
Size = \begin{bmatrix}
Line 181: Line 217:
\vdots\\  
\vdots\\  
d_n\text{ (mm)}\\  
d_n\text{ (mm)}\\  
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\quad


Feed= \begin{bmatrix}
\mathit{Feed}= \begin{bmatrix}
(Q_{M,F})_{11}\text{ (t/h)} & \dots & (Q_{M,F})_{1m}\text{ (t/h)}\\  
(Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\  
\vdots & \ddots & \vdots\\  
\vdots & \ddots & \vdots\\  
(Q_{M,F})_{n1}\text{ (t/h)} & \dots & (Q_{M,F})_{nm}\text{ (t/h)}\\  
(Q_{\rm M,F})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{nm}\text{ (t/h)}\\  
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\quad


OreSG= \begin{bmatrix}
\mathit{OreSG}= \begin{bmatrix}
(\rho_s)_1\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_s)_m\text{ (t/m}^\text{3}\text{)}\\  
(\rho_{\rm s})_1\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_{\rm s})_m\text{ (t/m}^\text{3}\text{)}\\  
\end{bmatrix}
\end{bmatrix},\quad
 
\mathit{Kd0}= \begin{bmatrix}
(K_{\rm d0})_1 & \dots & (K_{\rm d0})_m\\
\end{bmatrix}^*,\quad
 
\mathit{Kalpha 0}= \begin{bmatrix}
(K_{\alpha 0})_1 & \dots & (K_{\alpha 0})_m\\
\end{bmatrix}^*


\end{array}
</math>
</math>


Line 201: Line 246:
* <math>\text{Number of cyclones}</math> is the number of cyclones ''operating'' in a cluster. The number of cyclones is ignored if <math>\text{Pressure control}</math> is ''TRUE'' (the value is returned in the results instead)
* <math>\text{Number of cyclones}</math> is the number of cyclones ''operating'' in a cluster. The number of cyclones is ignored if <math>\text{Pressure control}</math> is ''TRUE'' (the value is returned in the results instead)
* <math>P</math>, the operating pressure, is ignored if <math>\text{Pressure control}</math> is ''FALSE'' (the value is returned in the results instead)
* <math>P</math>, the operating pressure, is ignored if <math>\text{Pressure control}</math> is ''FALSE'' (the value is returned in the results instead)
* <math>\rho_f</math> is the density of liquids (fluids) in the feed (t/m<sup>3</sup>)
* <math>\rho_{\rm f}</math> is the density of liquids (fluids) in the feed (t/m<sup>3</sup>)
* <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm)
* <math>m</math> is the number of ore types
* <math>m</math> is the number of ore types
* <math>Q_{M,F}</math> is feed solids mass flow rate by size and ore type (t/h)
* <math>Q_{\rm M,F}</math> is feed solids mass flow rate by size and ore type (t/h)
* <math>(Q_{M,F})_{Liquids}</math> is the mass flow feed rate of liquids into the cyclone (t/h)
* <math>(Q_{\rm M,F})_{\rm L}</math> is the mass flow feed rate of liquids into the cyclone (t/h)
* <math>^*</math> indicates optional arrays to specify cut size and sharpness parameters by ore/mineral/class type. If either array is omitted (default), the <math>K_{{\rm d0}}</math> and <math>K_{\alpha 0}</math>values supplied in the <math>\mathit{Parameters}</math> array are used instead.


=== Results ===
=== Results ===
Line 211: Line 258:


:<math>
:<math>
mdUnit\_Hydrocyclone\_NarasimhaMainza =  
\mathit{mdUnit\_Hydrocyclone\_NarasimhaMainza} =  
\begin{bmatrix}
\begin{bmatrix}


\begin{array}{c}
\begin{bmatrix}
\text{Number of cyclones}\\
\text{Number of cyclones}\\
\text{Qv per cyclone (m}^{\text{3}}\text{/h)}\\
\text{Qv per cyclone (m}^{\text{3}}\text{/h)}\\
\text{Qv per cluster (m}^{\text{3}}\text{/h)}\\
\text{Qv per cluster (m}^{\text{3}}\text{/h)}\\
C_V \text{ (}\%\text{ v/v)}\\
C_{\rm V} \text{ (}\%\text{ v/v)}\\
P\text{ (kPa)}\\
P\text{ (kPa)}\\
R_v\text{ (frac)}\\
R_{\rm v}\text{ (frac)}\\
R_f\text{ (frac)}\\
R_{\rm f}\text{ (frac)}\\
\text{Water split to OF (frac)}\\
\text{Water split to OF (frac)}\\
d_{50c}\text{ (mm)}\\
d_{\rm 50c}\text{ (mm)}\\
Q_m^{LiqOF}\text{ (t/h)}\\
(Q_{\rm M,OF})_{\rm L}\text{ (t/h)}\\
Q_m^{LiqUF}\text{ (t/h)}\\
(Q_{\rm M,UF})_{\rm L}\text{ (t/h)}\\
d_{50}\text{ (mm)}\\
d_{50}\text{ (mm)}\\
E_p\text{ (mm)}\\
E_{\rm p}\text{ (mm)}\\
I\\
I\\
\text{SPOC }C_{VU}\text{ (v/v)}\\
\text{SPOC }C_{\rm VU}\text{ (v/v)}\\
\text{Plitt }M_{SU}\text{ (m}^{3}\text{/h)}\\
\text{Plitt }M_{\rm SU}\text{ (m}^{3}\text{/h)}\\
\text{Plitt }\Phi_L\text{ (v/v)}\\
\text{Plitt }\Phi_{\rm L}\text{ (v/v)}\\
\text{Bustamante condition}\\
\text{Bustamante condition}\\
\text{Concha condition}\\
\text{Concha condition}\\
\end{array}
\end{bmatrix}




Line 249: Line 296:


\begin{bmatrix}
\begin{bmatrix}
(Q_{M,UF})_{11}\text{ (t/h)} & \dots & (Q_{M,UF})_{1m}\text{ (t/h)}\\
(Q_{\rm M,UF})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,UF})_{1m}\text{ (t/h)}\\
\vdots & \ddots & \vdots\\
\vdots & \ddots & \vdots\\
(Q_{M,UF})_{n1}\text{ (t/h)} & \dots & (Q_{M,UF})_{nm}\text{ (t/h)}\\
(Q_{\rm M,UF})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,UF})_{nm}\text{ (t/h)}\\
\end{bmatrix}
\end{bmatrix}


Line 257: Line 304:


\begin{bmatrix}
\begin{bmatrix}
(Q_{M,OF})_{11}\text{ (t/h)} & \dots & (Q_{M,OF})_{1m}\text{ (t/h)}\\
(Q_{\rm M,OF})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,OF})_{1m}\text{ (t/h)}\\
\vdots & \ddots & \vdots\\
\vdots & \ddots & \vdots\\
(Q_{M,OF})_{n1}\text{ (t/h)} & \dots & (Q_{M,OF})_{nm}\text{ (t/h)}\\
(Q_{\rm M,OF})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,OF})_{nm}\text{ (t/h)}\\
\end{bmatrix}
\end{bmatrix}


Line 265: Line 312:


\begin{bmatrix}
\begin{bmatrix}
(P_{OF})_1\text{ (mm)}\\
(E_{\rm oa})_{11}\text{ (frac)} & \dots & (E_{\rm oa})_{1m}\text{ (frac)}\\
\vdots & \ddots & \vdots\\
(E_{\rm oa})_{n1}\text{ (frac)} & \dots & (E_{\rm oa})_{nm}\text{ (frac)}\\
\end{bmatrix}
 
&
 
\begin{bmatrix}
(P_{\rm OF})_{1,{\rm All}}\\
\vdots\\
\vdots\\
(P_{OF})_n\text{ (mm)}
(P_{\rm OF})_{n,{\rm All}}\\
\end{bmatrix}
\end{bmatrix}


Line 273: Line 328:


\begin{bmatrix}
\begin{bmatrix}
(d_{50c})_1 & \dots & (d_{50c})_m\\
\alpha_1 & \dots & \alpha_m\\
(d_{\rm 50c})_1 & \dots & (d_{\rm 50c})_m\\
\beta^*_1 & \dots & \beta^*_m\\
\beta^*_1 & \dots & \beta^*_m\\
\end{bmatrix}\\
\end{bmatrix}\\
Line 305: Line 361:
* <math>\text{P}</math> is the pressure drop across the cyclone cluster with <math>\text{Number of cyclones}</math> operating at feed rate <math>\text{Qv per cluster}</math>, if <math>\text{Pressure control}</math> = ''FALSE'' (kPa)
* <math>\text{P}</math> is the pressure drop across the cyclone cluster with <math>\text{Number of cyclones}</math> operating at feed rate <math>\text{Qv per cluster}</math>, if <math>\text{Pressure control}</math> = ''FALSE'' (kPa)
* <math>\text{Water split to OF}</math> is actual split of liquids to the overflow (frac)
* <math>\text{Water split to OF}</math> is actual split of liquids to the overflow (frac)
* <math>(Q_{M,OF})_{Liquids}</math> is the mass flow rate of liquids to the overflow stream (t/h)
* <math>(Q_{\rm M,OF})_{\rm L}</math> is the mass flow rate of liquids to the overflow stream (t/h)
* <math>(Q_{M,UF})_{Liquids}</math> is the mass flow rate of liquids to the underflow stream (t/h)
* <math>(Q_{\rm M,UF})_{\rm L}</math> is the mass flow rate of liquids to the underflow stream (t/h)
* <math>Q_{M,UF}</math> is mass flow rate of solids to the underflow stream (t/h)
* <math>\text{SPOC }C_{\rm VU}</math> is the SPOC roping limit of volume fraction solids in the underflow stream (v/v)
* <math>Q_{M,OF}</math> is mass flow rate of solids to the overflow stream (t/h)
* <math>\text{Plitt }M_{\rm SU}</math> is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m<sup>3</sup>/h)
* <math>P_{OF}</math> is partition fraction of feed solids to the overflow stream (frac)
* <math>\text{Plitt }\Phi_{\rm L}</math> is the Plitt roping limit of volume fraction solids in the underflow stream (v/v)
* <math>\text{SPOC }C_{VU}</math> is the SPOC roping limit of volume fraction solids in the underflow stream (v/v)
* <math>\text{Plitt }M_{SU}</math> is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m<sup>3</sup>/h)
* <math>\text{Plitt }\Phi_L</math> is the Plit roping limit of volume fraction solids in the underflow stream (v/v)
* <math>\text{Bustamante condition}</math> is the underflow discharge type based on the Bustamante geometry limits (''spray'' or ''roping'' discharge)
* <math>\text{Bustamante condition}</math> is the underflow discharge type based on the Bustamante geometry limits (''spray'' or ''roping'' discharge)
* <math>\text{Concha condition}</math> is the underflow discharge type based on the Concha geometry limits (''spray'' or ''roping'' discharge)
* <math>\text{Concha condition}</math> is the underflow discharge type based on the Concha geometry limits (''spray'' or ''roping'' discharge)
* <math>Q_{\rm M,UF}</math> is mass flow rate of solids to the underflow stream (t/h)
* <math>Q_{\rm M,OF}</math> is mass flow rate of solids to the overflow stream (t/h)
* <math>(P_{\rm OF})_{i,{\rm All}}</math> is the actual partition of all particles of size <math>i</math> to the overflow stream, computed as <math>\frac{\sum_{j=1}^m(Q_{\rm M,OF})_{ij}}{\sum_{j=1}^m(Q_{\rm M,F})_{ij}}</math> (frac)


=== Example ===
=== Example ===
Line 329: Line 385:
The sections and variable names used in the SysCAD interface are described in detail in the following tables.
The sections and variable names used in the SysCAD interface are described in detail in the following tables.


{{SysCAD (Page, Hydrocyclone, ScdMD*Hydrocyclone)}}
{{SysCAD (Page, Hydrocyclone, DLL*Hydrocyclone)}}


==== Cyclone page ====
==== Cyclone page ====
Line 346: Line 402:
|CheckBox
|CheckBox
|If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate.
|If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate.
|-
|OreSpecific
|CheckBox
|Only appears if the Narasimha-Mazina (2014) model method is selected. If enabled, allows Kd0 and Kalpha parameters to be specified per species.
|-
|-
! colspan="3" style="text-align:left;" |''Dimensions''
! colspan="3" style="text-align:left;" |''Dimensions''
Line 401: Line 461:
|Kalpha0
|Kalpha0
|Input
|Input
|Calibration factor for the sharpness of separation eqaution.
|Calibration factor for the sharpness of separation equation.
|-
|-
|Beta
|Beta
Line 407: Line 467:
|'Fish hook' parameter of the Whiten-Beta efficiency curve equation.
|'Fish hook' parameter of the Whiten-Beta efficiency curve equation.


{{SysCAD (Text, Hydrocyclone, Liquids)}}
{{SysCAD (Text, Hydrocyclone, Liquids)|method=0}}


|-
|-
! colspan="3" style="text-align:left;" |''Results''
! colspan="3" style="text-align:left;" |''Results''
|-
|-
|ClusterQv
|ClusterQv / Cluster.Qv
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Volumetric flow rate of feed to the cyclone cluster (i.e. total flow).
|Volumetric flow rate of feed to the cyclone cluster (i.e. total flow).
|-
|-
|CycloneQv
|CycloneQv / Cyclone.Qv
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow).
|Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow).
|-
|-
|OperatingPressure
|OperatingPressure / P
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Pressure drop across the cyclone.
|Pressure drop across the cyclone.
|-
|-
|fv
|VolFracSolids / fv
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Volume fraction of solids in feed stream.
|Volume fraction of solids in feed stream.
|-
|-
|mur
|RelSlurryVisc / mur
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Relative slurry viscosity.
|Relative slurry viscosity.
Line 452: Line 512:
|}
|}


{{SysCAD (Page, Hydrocyclone, Partition)}}
{{SysCAD (Page, Hydrocyclone, Partition)|ActionU=Partition|ActionL=partition|DestinationU=Overflow|DestinationL=overflow|UnitL=cyclone}}


{{SysCAD (Page, Hydrocyclone, Roping)}}
{{SysCAD (Page, Hydrocyclone, Roping)}}


{{SysCAD (Page, About)}}
{{SysCAD (Page, About)}}
==== Additional notes ====
{{SysCAD (Text, No PSD Splits)|gasstream=overflow}}


== See also ==
== See also ==
Line 462: Line 526:
* [[Hydrocyclone (Plitt)]]
* [[Hydrocyclone (Plitt)]]
* [[Hydrocyclone (Nageswararao)]]
* [[Hydrocyclone (Nageswararao)]]
* [https://help.syscad.net/Met_Dynamics_-_Hydrocyclone Met Dynamics - Hydrocyclone (help.syscad.net)]
== External links ==
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Crushing_and_Grinding_Example Crushing and Grinding Example project (help.syscad.net)]
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Crushing,_Grinding_and_Flotation_Example Crushing, Grinding and Flotation Example project (help.syscad.net)]
* [https://help.syscad.net/Example_-_09_Met_Dynamics_Projects#Gravity,_Dense_Medium_and_Magnetic_Separation_Example Gravity, Dense Medium, and Magnetic Separation Example project (help.syscad.net)]
* [https://help.syscad.net/Met_Dynamic_-_Dynamic_Example_Projects#Dynamic_Grinding_Example Dynamic Grinding Example project (help.syscad.net)]


== References ==
== References ==
Line 475: Line 547:


:<math>
:<math>
\dfrac {(d_{50c})_i}{D_c} = K_{d0} {\left( \dfrac {D_o} {D_c} \right)}^{d_1} {\left( \dfrac {D_u} {D_c} \right)}^{d_2} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{d_3} (\text{Re})^{d_4} {\left( \dfrac {D_i} {D_c} \right)}^{d_5} {\left( \dfrac {L_c} {D_c} \right)}^{d_6} {\big( \tan (d_7 \theta) \big)}^{d_8} {\left( \cos \left( \dfrac i 2 \right) \right)}^{d_9} {\left( \dfrac {\rho_s - \rho_f}{\rho_f} \right)}^{d_{10}} {\left( \dfrac {\rho_{si} - \rho_f}{\rho_f} \right)}^{d_{11}}
\dfrac {(d_{\rm 50c})_i}{D_{\rm c}} = K_{\rm d0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{d_1} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{d_2} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{d_3} (\text{Re})^{d_4} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{d_5} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{d_6} {\big( \tan (d_7 \theta) \big)}^{d_8} {\left( \cos \left( \dfrac i 2 \right) \right)}^{d_9} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{d_{10}} {\left( \dfrac {\rho_{si} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{d_{11}}
</math>
</math>


:<math>
:<math>
R_f = K_{w0} {\left( \dfrac {D_o} {D_c} \right)}^{w_1} {\left( \dfrac {D_u} {D_c} \right)}^{w_2} {\left( \dfrac {V^2_t} {R_{max}g} \right)}^{w_3} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{w_4} {\mu_r}^{w_5} {\left( \dfrac {L_c} {D_c} \right)}^{w_6} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{w_7} {\left( \dfrac {\rho_s - \rho_f} {\rho_f} \right)}^{w_8} {\left( \cos \left(\dfrac i 2 \right) \right)}^{w_9}
R_{\rm f} = K_{\rm w0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{w_1} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{w_2} {\left( \dfrac {V^2_t} {R_{\rm max}g} \right)}^{w_3} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{w_4} {\mu_{\rm r}}^{w_5} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{w_6} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{w_7} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}} {\rho_{\rm f}} \right)}^{w_8} {\left( \cos \left(\dfrac i 2 \right) \right)}^{w_9}
</math>
</math>


:<math>
:<math>
\alpha_i = K_\alpha {{ {{\left( \dfrac {D_o} {D_c} \right)}^{\alpha_1} {\left( \dfrac {V_t^2} {gR_{max}} \right)}^{\alpha_2} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{\alpha_3} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_v}} \right)}^{\alpha_4}} } { {{\left( \dfrac {D_u} {D_c} \right)}^{\alpha_5} {\left( \dfrac {\left( \rho_s - \rho_p \right)} {\rho_s} \right)}^{\alpha_6} {\mu_r}^{\alpha_7} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{\alpha_8} {\left( \dfrac {L_c} {D_c} \right)}^{\alpha_9}} }} \left( \rho_s - \rho_p \right)^{\alpha_{10}}
\alpha_i = K_\alpha {{ {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{\alpha_1} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{\alpha_2} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{\alpha_3} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{\alpha_4}} } { {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{\alpha_5} {\left( \dfrac {\left( \rho_{\rm s} - \rho_{\rm p} \right)} {\rho_{\rm s}} \right)}^{\alpha_6} {\mu_{\rm r}}^{\alpha_7} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{\alpha_8} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{\alpha_9}} }} \left( \rho_{\rm s} - \rho_{\rm p} \right)^{\alpha_{10}}
</math>
</math>


:<math>
:<math>
Q = K_{Q0} {\left( \dfrac {D_i} {D_c} \right)}^{Q_1} {D_c}^{2} \sqrt \dfrac P {\rho_p} {\left( \dfrac {D_o} {d_c} \right)}^{Q_2} {\left( \dfrac {D_u} {D_c} \right)}^{Q_3} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{Q_4} {\left( \dfrac {L_c} {D_c} \right)}^{Q_5} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{Q_6} {\left( \cos \left( \dfrac i 2 \right) \right)}^{Q_7}
Q = K_{\rm Q0} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{Q_1} {D_{\rm c}}^{2} \sqrt \dfrac P {\rho_{\rm p}} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{Q_2} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{Q_3} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{Q_4} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{Q_5} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{Q_6} {\left( \cos \left( \dfrac i 2 \right) \right)}^{Q_7}
</math>
</math>


:<math>
:<math>
P = \rho_p \left [ Q {{K_{Q0}}^{-1} {\left( \dfrac {D_i} {D_c} \right)}^{-Q_1} {D_c}^{-2} {\left( \dfrac {D_o} {d_c} \right)}^{-Q_2} {\left( \dfrac {D_u} {D_c} \right)}^{-Q_3} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-Q_4} {\left( \dfrac {L_c} {D_c} \right)}^{-Q_5} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-Q_6} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-Q_7}} \right ]^2
P = \rho_{\rm p} \left [ Q {{K_{\rm Q0}}^{-1} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-Q_1} {D_{\rm c}}^{-2} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{-Q_2} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-Q_3} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-Q_4} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-Q_5} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-Q_6} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-Q_7}} \right ]^2
</math>
</math>


Line 503: Line 575:


:<math>
:<math>
\dfrac {d_{50c}}{D_c} =
\dfrac {d_{\rm 50c}}{D_{\rm c}} =
\begin{cases}
\begin{cases}
K_{d0} {\left( \dfrac {D_o}{D_c} \right)}^{1.207} {\left( \dfrac {D_u}{D_c} \right)}^{-0.921} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.657} (\text{Re})^{-0.500} {\left( \dfrac {D_i}{D_c} \right)}^{-0.750} {\left( \dfrac {L_c}{D_c} \right)}^{0.272} {\left( \dfrac {\tan \theta}{2} \right)}^{0.139}\phantom{00} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{-1.050} {\left( \dfrac {\rho_s - \rho_f}{\rho_f} \right)}^{-0.244} & \text{Narasimha (2009)}\\
K_{\rm d0} {\left( \dfrac {D_{\rm o}}{D_{\rm c}} \right)}^{1.207} {\left( \dfrac {D_{\rm u}}{D_{\rm c}} \right)}^{-0.921} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.657} (\text{Re})^{-0.500} {\left( \dfrac {D_{\rm i}}{D_{\rm c}} \right)}^{-0.750} {\left( \dfrac {L_{\rm c}}{D_{\rm c}} \right)}^{0.272} {\left( \dfrac {\tan \theta}{2} \right)}^{0.139}\phantom{00} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{-1.050} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{-0.244} & \text{Narasimha (2009)}\\
\\
\\
K_{d0} {\left( \dfrac {D_o} {D_c} \right)}^{1.093} {\left( \dfrac {D_u} {D_c} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_i} {D_c} \right)}^{-0.936} {\left( \dfrac {L_c} {D_c} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_s - \rho_f}{\rho_f} \right)}^{-0.217} & \text{Narasimha et al. (2014)}\\
K_{\rm d0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{1.093} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.936} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{-0.217} & \text{Narasimha et al. (2014)}\\
\end{cases}
\end{cases}
</math>
</math>


:<math>
:<math>
R_f =  
R_{\rm f} =  
\begin{cases}
\begin{cases}
K_{w0} {\left( \dfrac {D_o} {D_c} \right)}^{-0.835\phantom{00}} {\left( \dfrac {D_u} {D_c} \right)}^{2.190\phantom{0}} {\left( \dfrac {V^2_t} {R_{max}g} \right)}^{-0.259\phantom{00}} {\left( {\tan \left( \dfrac{\theta}{2}\right)}  \right)}^{-0.649} {\mu_r}^{-0.792\phantom{0}} {\left( \dfrac {L_c} {D_c} \right)}^{1.937} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.930} {\left( \dfrac {\rho_s - \rho_f} {\rho_f} \right)}^{0.462} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.765} & \text{Narasimha (2009)}\\
K_{\rm w0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{-0.835\phantom{00}} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{2.190\phantom{0}} {\left( \dfrac {V^2_t} {R_{\rm max}g} \right)}^{-0.259\phantom{00}} {\left( {\tan \left( \dfrac{\theta}{2}\right)}  \right)}^{-0.649} {\mu_{\rm r}}^{-0.792\phantom{0}} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{1.937} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.930} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}} {\rho_{\rm f}} \right)}^{0.462} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.765} & \text{Narasimha (2009)}\\
\\
\\
K_{w0} {\left( \dfrac {D_o} {D_c} \right)}^{-1.06787} {\left( \dfrac {D_u} {D_c} \right)}^{2.2062} {\left( \dfrac {V^2_t} {R_{max}g} \right)}^{-0.20472} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{-0.829} {\mu_r}^{-0.7118} {\left( \dfrac {L_c} {D_c} \right)}^{2.424} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.8843} {\left( \dfrac {\rho_s - \rho_f} {\rho_f} \right)}^{0.523} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.793} & \text{Narasimha et al. (2014)}\\
K_{\rm w0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{-1.06787} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{2.2062} {\left( \dfrac {V^2_t} {R_{\rm max}g} \right)}^{-0.20472} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{-0.829} {\mu_{\rm r}}^{-0.7118} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{2.424} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.8843} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}} {\rho_{\rm f}} \right)}^{0.523} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.793} & \text{Narasimha et al. (2014)}\\
\end{cases}
\end{cases}
</math>
</math>
Line 523: Line 595:
\alpha =
\alpha =
\begin{cases}
\begin{cases}
K_\alpha {{\left( \dfrac {D_o} {D_c} \right)}^{0.191} {\left( \dfrac {V_t^2} {gR_{max}} \right)}^{0.012} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.751} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_v}} \right)}^{0.739}} {{\left( \dfrac {D_u} {D_c} \right)}^{-0.467} {\left( \dfrac {\left( \rho_s - \rho_p \right)} {\rho_s} \right)}^{-1.670} {\mu_r}^{-0.112} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.018} {\left( \dfrac {L_c} {D_c} \right)}^{-0.233}} & \text{Narasimha (2009)}\\
K_\alpha {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{0.191} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{0.012} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.751} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.739}} {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.467} {\left( \dfrac {\left( \rho_{\rm s} - \rho_{\rm p} \right)} {\rho_{\rm s}} \right)}^{-1.670} {\mu_{\rm r}}^{-0.112} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.018} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.233}} & \text{Narasimha (2009)}\\
\\
\\
K_\alpha {{ {{\left( \dfrac {D_o} {D_c} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_t^2} {gR_{max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_v}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_u} {D_c} \right)}^{-0.567} {\left( \dfrac {\left( \rho_s - \rho_p \right)} {\rho_s} \right)}^{-1.837} {\mu_r}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_c} {D_c} \right)}^{-0.2}} }} & \text{Narasimha et al. (2014)}\\
K_\alpha {{ {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.567} {\left( \dfrac {\left( \rho_{\rm s} - \rho_{\rm p} \right)} {\rho_{\rm s}} \right)}^{-1.837} {\mu_{\rm r}}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.2}} }} & \text{Narasimha et al. (2014)}\\
\end{cases}
\end{cases}
</math>
</math>
Line 532: Line 604:
Q =  
Q =  
\begin{cases}
\begin{cases}
K_{Q0} {\left( \dfrac {D_i} {D_c} \right)}^{0.45} {D_c}^{2} \sqrt \dfrac P {\rho_p} {\left( \dfrac {D_o} {D_c} \right)}^{1.250} {\left( \dfrac {D_u} {D_c} \right)}^{0.060} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_c} {D_c} \right)}^{0.330} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.047} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.090} & \text{Narasimha (2009)}\\
K_{\rm Q0} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{0.45} {D_{\rm c}}^{2} \sqrt \dfrac P {\rho_{\rm p}} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{1.250} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{0.060} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.330} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.047} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.090} & \text{Narasimha (2009)}\\
\\
\\
K_{Q0} {\left( \dfrac {D_i} {D_c} \right)}^{0.45} {D_c}^{2} \sqrt \dfrac P {\rho_p} {\left( \dfrac {D_o} {d_c} \right)}^{1.099} {\left( \dfrac {D_u} {D_c} \right)}^{0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_c} {D_c} \right)}^{0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.092} & \text{Narasimha et al. (2014)}\\
K_{\rm Q0} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{0.45} {D_{\rm c}}^{2} \sqrt \dfrac P {\rho_{\rm p}} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{1.099} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.092} & \text{Narasimha et al. (2014)}\\
\end{cases}
\end{cases}
</math>
</math>
Line 541: Line 613:
P =  
P =  
\begin{cases}
\begin{cases}
\rho_p \left [ Q {{K_{Q0}}^{-1} {\left( \dfrac {D_i} {D_c} \right)}^{-0.45} {D_c}^{-2} {\left( \dfrac {D_o} {D_c} \right)}^{-1.250} {\left( \dfrac {D_u} {D_c} \right)}^{-0.060} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_c} {D_c} \right)}^{-0.330} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{0.047} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.090}} \right ]^2 & \text{Narasimha (2009)}\\
\rho_{\rm p} \left [ Q {{K_{\rm Q0}}^{-1} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.45} {D_{\rm c}}^{-2} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{-1.250} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.060} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.330} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.047} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.090}} \right ]^2 & \text{Narasimha (2009)}\\
\\
\\
\rho_p \left [ Q {{K_{Q0}}^{-1} {\left( \dfrac {D_i} {D_c} \right)}^{-0.45} {D_c}^{-2} {\left( \dfrac {D_o} {d_c} \right)}^{-1.099} {\left( \dfrac {D_u} {D_c} \right)}^{-0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_c} {D_c} \right)}^{-0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.092}} \right ]^2 & \text{Narasimha et al. (2014)}\\
\rho_{\rm p} \left [ Q {{K_{\rm Q0}}^{-1} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.45} {D_{\rm c}}^{-2} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{-1.099} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.092}} \right ]^2 & \text{Narasimha et al. (2014)}\\
\end{cases}
\end{cases}
</math>
</math>


--->
--->

Latest revision as of 13:31, 1 May 2025

Description

This article describes the Narasimha-Mainza model for hydrocyclone size classification.

Narasimha et al. (2014a) describe an empirical hydrocyclone model that improves on the Plitt and Nageswararao approaches with the addition of several features:[1]

  • A sharpness of separation equation
  • A slurry viscosity term that includes the effects of very fine particles
  • Terms for cyclone inclination, particle density, g-forces, flow regime (Reynolds Number) and turbulent diffusion

Narasimha et al. (2014b) subsequently presented a multi-component version of the same model, with revised equations for cut size and sharpness of separation per ore component:[2]

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Efficiency curve

Corrected cut size

Liquids recovery

Sharpness of separation

Cyclone capacity

Multi-component modelling

Narasimha, Mainza and Holtham (2014)

Silveira, Delboni and Bergerman (2024)

Partition metrics

Roping

Additional notes

Note that the equations presented by Narasimha et al. (2014) differ from those presented in Narasimha's original dissertation.[3]

The user should be aware of which model formulation is being applied when adopting calibration parameters from external sources. Recalibration of model parameters via the Excel interface below is recommended in such cases.

Excel

The Narasimha-Mainza hydrocyclone model may be invoked from the Excel formula bar with the following function call: 

=mdUnit_Hydrocyclone_NarasimhaMainza(Parameters as Range, Size as Range, Feed as Range, OreSG Range, Optional Kd0 as Range, Optional Kalpha0 as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

Inputs

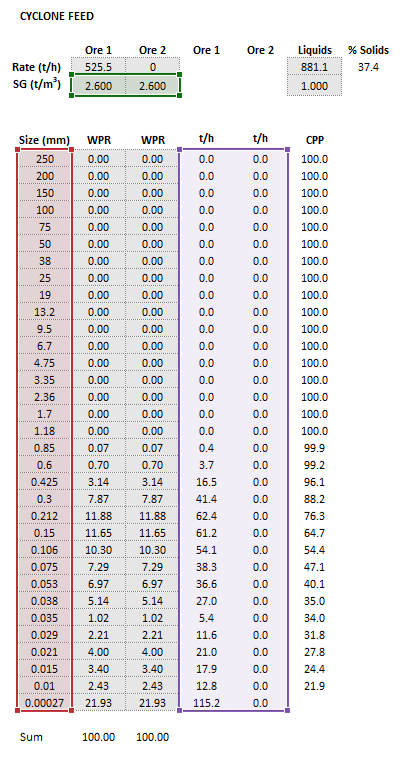
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:


where:

  • is the set of equations to use (0 = Narasimha et al. (2014), 1 = Narasimha et al. (Multi))
  • indicates whether the number of cyclones required at the given feed flow rate and pressure set point is returned (TRUE) or the operating pressure at the given feed flowrate and number of cyclones is returned (FALSE)
  • is the number of cyclones operating in a cluster. The number of cyclones is ignored if is TRUE (the value is returned in the results instead)
  • , the operating pressure, is ignored if is FALSE (the value is returned in the results instead)
  • is the density of liquids (fluids) in the feed (t/m3)
  • is the size of the square mesh interval that feed mass is retained on (mm)
  • is the number of ore types
  • is feed solids mass flow rate by size and ore type (t/h)
  • is the mass flow feed rate of liquids into the cyclone (t/h)
  • indicates optional arrays to specify cut size and sharpness parameters by ore/mineral/class type. If either array is omitted (default), the and values supplied in the array are used instead.

Results

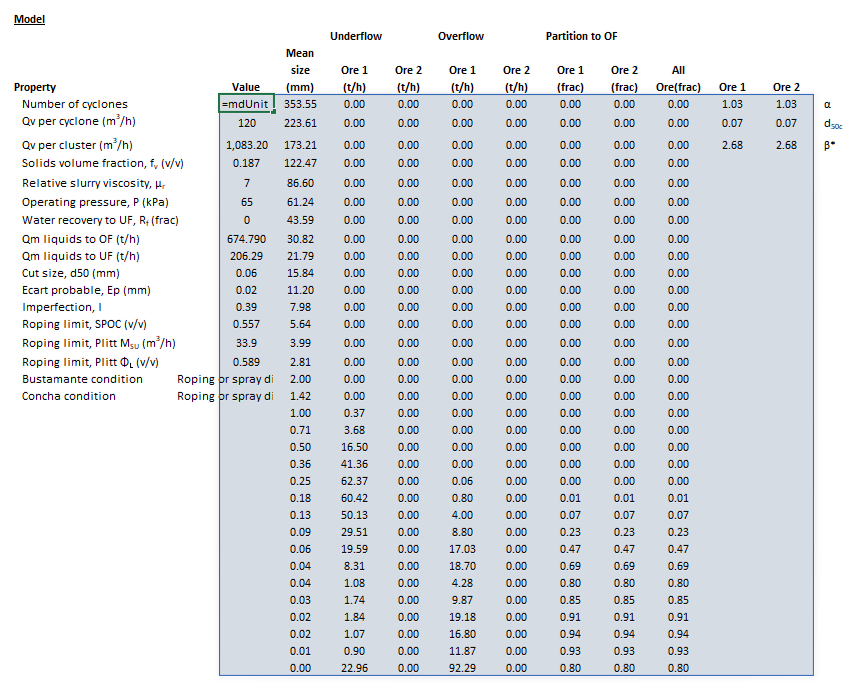
The results are displayed in Excel as an array corresponding to the matrix notation below:


where:

  • is the number of cyclones required at the given and operating pressure , if = TRUE
  • is the volumetric feed flow rate per cyclone (m3/h)
  • is the total volumetric feed flow rate to the cluster of cyclones (m3/h)
  • is the pressure drop across the cyclone cluster with operating at feed rate , if = FALSE (kPa)
  • is actual split of liquids to the overflow (frac)
  • is the mass flow rate of liquids to the overflow stream (t/h)
  • is the mass flow rate of liquids to the underflow stream (t/h)
  • is the SPOC roping limit of volume fraction solids in the underflow stream (v/v)
  • is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m3/h)
  • is the Plitt roping limit of volume fraction solids in the underflow stream (v/v)
  • is the underflow discharge type based on the Bustamante geometry limits (spray or roping discharge)
  • is the underflow discharge type based on the Concha geometry limits (spray or roping discharge)
  • is mass flow rate of solids to the underflow stream (t/h)
  • is mass flow rate of solids to the overflow stream (t/h)
  • is the actual partition of all particles of size to the overflow stream, computed as (frac)

Example

The images below show the selection of input arrays and output results in the Excel interface.

Figure 2. Example showing the selection of the Parameters (blue frame) array in Excel.
Figure 3. Example showing the selection of the Size (red frame), Feed (purple frame) and OreSG (green frame) arrays in Excel.
Figure 4. Example showing the outline of the Results (light blue frame) array in Excel.

SysCAD

The sections and variable names used in the SysCAD interface are described in detail in the following tables.

MD_Hydrocyclone page

The first tab page in the access window will have this name.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Tag Display This name tag may be modified with the change tag option.
Condition Display OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount Display The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc Display This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.

If this field is blank, then SysCAD will display the unit class ID.

Requirements
On CheckBox This enables the unit. If this box is not checked, then the MassFracToUF option appears below.
MassFracToUF Input Only appears if the On field above is not checked. Specifies the fraction of feed mass that reports to the underflow stream when the model is off.
Method Partition (User) The partition to overflow for each size interval is defined by the user. Different values can be used for different solids.
Partition (Reid-Plitt) The partition to overflow for each size interval is defined by a Reid-Plitt efficiency curve. Different parameters can be used for different solids.
Partition (Whiten-Beta) The partition to overflow for each size interval is defined by a Whiten-Beta efficiency curve. Different parameters can be used for different solids.
Nageswararao The Nageswararao model is used to determine the partition of solids to underflow and overflow for each size interval.
Narasimha-Mainza (2014) The Narasimha-Mainza (2014) model is used to determine the partition of solids to underflow and overflow for each size interval.
Narasimha-Mainza (Multi) The Narasimha-Mainza (Multi) model is used to determine the partition of solids to underflow and overflow for each size interval.
Plitt The Plitt model is used to determine the partition of solids to underflow and overflow for each size interval.
RopingCalcs CheckBox Show addition calculations that predict the onset of cyclone underflow roping.
Options
ShowQFeed CheckBox QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream.
ShowQOF CheckBox QOF and associated tab pages (eg Sp) will become visible, showing the properties of the overflow stream.
ShowQUF CheckBox QUF and associated tab pages (eg Sp) will become visible, showing the properties of the underflow stream.
SizeForPassingFracCalc Input Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section.
FracForPassingSizeCalc Input Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section.
Stream Summary
MassFlow / Qm Display The total mass flow in each stream.
SolidMassFlow / SQm Display The Solids mass flow in each stream.
LiquidMassFlow / LQm Display The Liquid mass flow in each stream.
VolFlow / Qv Display The total Volume flow in each stream.
Temperature / T Display The Temperature of each stream.
Density / Rho Display The Density of each stream.
SolidFrac / Sf Display The Solid Fraction in each stream.
LiquidFrac / Lf Display The Liquid Fraction in each stream.
Passing Display The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream.
Passes Display The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction.

Cyclone page

The Cyclone page is used to specify the input parameters for the hydrocyclone model.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
NarasimhaMainza
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
PressureControl CheckBox If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate.
OreSpecific CheckBox Only appears if the Narasimha-Mazina (2014) model method is selected. If enabled, allows Kd0 and Kalpha parameters to be specified per species.
Dimensions
NumberCyclones / NumCyclones Input The number of operating cyclone units in the cluster.
CycloneDiameter / Dc Input Diameter of the cyclone.
InletDiameter / Di Input Diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet.
CycloneDiameter / Dc Input Diameter of the cyclone.
OverflowDiameter / Do Input Diameter of the vortex finder (overflow).
UnderflowDiameter / Du Input Diameter of the apex/spigot (underflow).
CylSectLength / Lc Input Length of the cylindrical section of the cyclone.
ConeFullAngle / Theta Input Full angle of the cone section of the cyclone.
InclinationAngle/ i Input Angle of inclination of cyclone from the vertical.
Parameters
Kd0 Input Calibration factor for the d50c equation.
KQ0 Input Calibration factor for the pressure-flowrate equation
Kw0 Input Calibration factor for the liquids recovery to underflow equation.
Kalpha0 Input Calibration factor for the sharpness of separation equation.
Beta Input 'Fish hook' parameter of the Whiten-Beta efficiency curve equation.
Liquids
LiquidsSeparMethod Split To UF (User) Liquids are split to underflow by a user-defined fraction of liquids in the feed.
Split To UF (Model) Liquids are split to underflow by a fraction computed by the associated model.
UF Solids Fraction Sufficient liquids mass is recovered to the underflow stream to yield the user-defined underflow solids mass fraction value (if possible).
UF Liquids Fraction Sufficient liquids mass is recovered to the underflow stream to yield the user-defined underflow liquids mass fraction value (if possible).
UFSolidsFracReqd / UF.SfReqd Input Required value of the mass fraction of solids in the underflow stream. Only visible if UF Solids Fraction is selected.
UFLiquidsFracReqd / UF.LfReqd Input Required value of the mass fraction of liquids in the underflow stream. Only visible if UF Liquids Fraction is selected.
LiqSplitToUF / UF.LiqSplit Input/Display The fraction of liquids recovered to underflow.
Results
ClusterQv / Cluster.Qv Display Volumetric flow rate of feed to the cyclone cluster (i.e. total flow).
CycloneQv / Cyclone.Qv Display Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow).
OperatingPressure / P Display Pressure drop across the cyclone.
VolFracSolids / fv Display Volume fraction of solids in feed stream.
RelSlurryVisc / mur Display Relative slurry viscosity.
Rf Display Fraction of feed liquids recovered to underflow stream.
d50 Display The separation size, d50, of all solid particles in the feed.
EcartProbable / Ep Display The value of the Ecart Probable of the separation.
Imperfection / I Display The value of the Imperfection of the separation.
Alpha Display Value of , per species.
d50c Display Value of the corrected d50c, per species.
Beta* Display Value of , per species.

Partition page

The Partition page is used to display (or specify) the partition by species/component/element/individual phase and size values.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Distribution
Name Display Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream.
IntervalCount Display Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream.
SpWithPSDCount Display Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality.
Partition
Method Model/User Select model-calculated or user-defined partition to separate each solids species type.
Density Display Density of each solid species.
Size Display Size of each interval in mesh series.
MeanSize Display Geometric mean size of each interval in mesh series.
All (All column) Display
  • Actual overall partition to overflow of all solid species, for each size interval.
  • Excludes solid species not present in the cyclone feed.
Partition Display
  • Partition to overflow for each size interval, in each solid species, as determined by the selected model or user defined value.
  • Note: These values are displayed regardless of whether the solid species is present in the cyclone feed or not.
All (All row, All column) Display
  • Displays the actual, total, partition of all solids with a particle size distribution property in the feed to overflow.
  • Excludes solid species not present in the cyclone feed.
All (All row, per species) Display
  • Actual overall partition to overflow for each solid species, for all size intervals in that species.
  • Excludes solid species not present in the cyclone feed.
CmpPartition
Components
ButtonHideComponents.png
ButtonShowComponents.png
 Hides or shows component partition table.
Size Display Size of each interval in mesh series.
MeanSize Display Geometric mean size of each interval in mesh series.
All (All column) Display
  • Actual overall partition to overflow of all solid components, for each size interval.
  • Excludes solid components not present in the cyclone feed.
CmpPartition Display
  • Partition to overflow for each size interval, in each solid component, as determined by the selected model or user defined value.
  • Excludes solid components not present in the cyclone feed.
All (All row, All column) Display
  • Displays the actual, total, partition of all solid components with a particle size distribution property in the feed to overflow.
  • Excludes solid components not present in the cyclone feed.
All (All row, per component) Display
  • Actual overall partition to overflow for each solid component, for all size intervals in that component.
  • Excludes solid components not present in the cyclone feed.
ElePartition
Elements
ButtonHideElements.png
ButtonShowElements.png
 Hides or shows element partition table.
Size Display Size of each interval in mesh series.
MeanSize Display Geometric mean size of each interval in mesh series.
All (All column) Display
  • Actual overall partition to overflow of all solid elements, for each size interval.
  • Excludes solid elements not present in the cyclone feed.
ElePartition Display
  • Partition to overflow for each size interval, in each solid element, as determined by the selected model or user defined value.
  • Excludes solid elements not present in the cyclone feed.
All (All row, All column) Display
  • Displays the actual, total, partition of all solid elements with a particle size distribution property in the feed to overflow.
  • Excludes solid elements not present in the cyclone feed.
All (All row, per element) Display
  • Actual overall partition to overflow for each solid element, for all size intervals in that component.
  • Excludes solid elements not present in the cyclone feed.
IPhPartition
IPhases
ButtonHideIPhases.png
ButtonShowIPhases.png
 Hides or shows individual phases partition table.
Size Display Size of each interval in mesh series.
MeanSize Display Geometric mean size of each interval in mesh series.
All (All column) Display
  • Actual overall partition to overflow of all solid individual phases, for each size interval.
  • Excludes solid individual phases not present in the cyclone feed.
IPhPartition Display
  • Partition to overflow for each size interval, in each solid individual phase, as determined by the selected model or user defined value.
  • Excludes solid individual phases not present in the cyclone feed.
All (All row, All column) Display
  • Displays the actual, total, partition of all solid individual phases with a particle size distribution property in the feed to overflow.
  • Excludes solid individual phases not present in the cyclone feed.
All (All row, per individual phase) Display
  • Actual overall partition to overflow for each solid individual phase, for all size intervals in that component.
  • Excludes solid individual phases not present in the cyclone feed.

Roping page

This page displays the results for hydrocyclone roping limit calculations. The page is only visible if Roping is selected on the MD_Hydrocyclone page.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Roping
Underflow
SolidsVolFlow / SQv Display Volumetric flow rate of solids in cyclone underflow stream.
Plitt.MSu Display Plitt's volumetric flow rate of solids in cyclone underflow roping limit.
SolidsVolFrac / Svf Display Volume fraction of solids in the cyclone underflow stream.
SPOC Display SPOC volume fraction of solids in the cyclone underflow roping limit.
Plitt.phiL Display Plitt's volume fraction of solids in the cyclone underflow roping limit.
Geometry
BCondition Display Text string describing the spray/roping condition of the cyclone based on Bustamante's geometry limits.
CCondition Display Text string describing the spray/roping condition of the cyclone based on the Concha et al. geometry limits.

About page

This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
About
HelpLink ButtonLicensingHelp.png Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required.
Information ButtonCopyToClipboard.png Copies Product and License information to the Windows clipboard.
Product
Name Display Met Dynamics software product name
Version Display Met Dynamics software product version number.
BuildDate Display Build date and time of the Met Dynamics Models SysCAD Add-On.
License
File ButtonBrowse.png This is used to locate a Met Dynamics software license file.
Location Display Type of Met Dynamics software license or file name and path of license file.
SiteCode Display Unique machine identifier for license authorisation.
ReqdAuth Display Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime.
Status Display License status, LICENSE_OK indicates a valid license, other messages report licensing errors.
IssuedTo Display Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to.
ExpiryDate Display Only visible if Met Dynamics license file is used. License expiry date.
DaysLeft Display Only visible if Met Dynamics license file is used. Days left before the license expires.

Additional notes

  • Solid species that do not possess a particle size distribution property are split according to the overall mass split of the default particle size distribution species selected in the SysCAD Project Configuration.
  • If the default particle size distribution species is not present in the unit feed, the overall split of all other species with particle size distributions combined is used, as determined by the model.
  • Gas phase species report directly to the overflow stream without split.

See also

External links

References

  1. ↑ Narasimha, M., Mainza, A.N., Holtham, P.N., Powell, M.S. and Brennan, M.S., 2014. A semi-mechanistic model of hydrocyclones—Developed from industrial data and inputs from CFD. International Journal of Mineral Processing, 133, pp.1-12.
  2. ↑ Narasimha, M., Crasta, J, Sreenivas, T. and Mainza, A. N., 2014. Performance of hydrocyclone separating bi-component mixture. In Proceedings of the XXVII International Mineral Processing Congress, Santiago, Chile, 2014.
  3. ↑ Narasimha, M., 2009. Improved Computational and Empirical Models of Hydrocyclones. PhD Thesis, University of Queensland (unpublished).
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Hydrocyclone_(Narasimha-Mainza)&oldid=2583"