Tumbling Mill (Power, Hogg and Fuerstenau): Difference between revisions

Latest revision as of 08:31, 26 March 2023

Description

This article describes the Hogg and Fuerstenau (1972) method for estimating the power draw of a tumbling mill.^[1]

Model theory

Figure 1. Tumbling mill profile showing the charge shape and lift angle assumptions of the Hogg and Fuerstenau power draw model.

The Hogg and Fuerstenau method adopts the simplified charge geometry shown in Figure 1, and computes mill power as:^[2]

P_{\rm {net}}=\eta P_{\rm {gross}}=0.238D^{3.5}\left({\frac {L}{D}}\right)N_{\rm {c}}\rho _{\rm {ap}}(J-1.065J^{2})sin\alpha

where:

$P_{\rm {net}}$ is the net power draw of the mill, i.e. excluding mill drive losses (kW)
$P_{\rm {gross}}$ is the gross power draw of the mill, i.e. including mill drive losses (kW)
$\eta$ is the mill drive efficiency (kW/kW)
$D$ is mill diameter (ft)
$L$ is mill length (ft)
$N_{\rm {c}}$ is mill fraction critical speed (frac)
$\rho _{\rm {ap}}$ is the apparent density of the mill charge (t/m³)
$J$ is the volumetric fraction of the mill filled with charge, including balls and interstitial voids between balls (v/v)
$\alpha$ is the charge lift angle (degrees)

The apparent charge density, $\rho _{\rm {ap}}$ , may be computed as:

\rho _{\rm {ap}}={\begin{cases}{\dfrac {(1-f_{\rm {v}})\rho _{\rm {b}}J_{\rm {b}}+(1-f_{\rm {v}})\rho _{\rm {m}}(J-J_{\rm {b}})+\rho _{\rm {p}}J_{\rm {p}}f_{\rm {v}}J}{J}}&{\text{for autogenous or semi-autogenous mills}}\\{\dfrac {(1-f_{\rm {v}})\rho _{\rm {b}}J_{\rm {b}}+\rho _{\rm {p}}J_{\rm {p}}f_{\rm {v}}J_{\rm {b}}+\rho _{\rm {p}}(J-J_{\rm {b}})}{J}}&{\text{for ball or rod mills}}\end{cases}}

where:

$f_{\rm {v}}$ is the volumetric fraction of interstitial void space in the charge (usually 0.4) (v/v)
$\rho _{\rm {b}}$ is the density of balls (t/m³)
$\rho _{\rm {m}}$ is the density of solid ore particles (t/m³)
$\rho _{\rm {p}}$ is the density of slurry (t/m³)
$J_{\rm {b}}$ is the volumetric fraction of the mill filled with balls, including slurry and interstitial voids between balls (v/v)
$J_{\rm {p}}$ is the volumetric fraction of the interstitial charge void space occupied by slurry (v/v)

Slurry density, $\rho _{\rm {p}}$ , may be computed as:

\rho _{\rm {p}}={\dfrac {1}{{\dfrac {f_{\rm {s}}}{\rho _{\rm {m}}}}+(1-f_{\rm {s}})}}

where $f_{\rm {s}}$ is the mass fraction of solids in the slurry (w/w).

The net power draw, $P_{\rm {net}}$ , may be separated into its contributing constituents:

P_{\rm {b}}=\left({\frac {(1-f_{\rm {v}})\rho _{\rm {b}}J_{\rm {b}}}{\rho _{\rm {ap}}J}}\right)\cdot P_{\rm {net}}

P_{\rm {r}}=\left({\frac {(1-f_{\rm {v}})\rho _{\rm {m}}(J-J_{\rm {b}})}{\rho _{\rm {ap}}J}}\right)\cdot P_{\rm {net}}

P_{\rm {s}}=\left({\frac {\rho _{\rm {p}}J_{\rm {p}}f_{\rm {v}}J_{\rm {b}}}{\rho _{\rm {ap}}J}}\cdot \right)\cdot P_{\rm {net}}

P_{\rm {o}}=\left({\frac {\rho _{\rm {p}}(J-J_{\rm {b}})}{\rho _{\rm {ap}}J}}\cdot \right)\cdot P_{\rm {net}}

where:

$P_{\rm {b}}$ is the power drawn by the ball component of the mill load (kW)
$P_{\rm {r}}$ is the power drawn by the rock (coarse ore) component of the mill load (kW). Autogenous and semi-autogenous mills only.
$P_{\rm {s}}$ is the power drawn by the interstitial slurry component of the mill load (kW)
$P_{\rm {o}}$ is the power drawn by the overfilling, or excess, slurry component of the mill load (when the interstitial voids are completely filled with slurry (kW). Ball mills only.

Excel

The Hogg and Fuerstenau mill power model may be invoked from the Excel formula bar with the following function call:

=mdMillPower_HoggFuerstenau(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

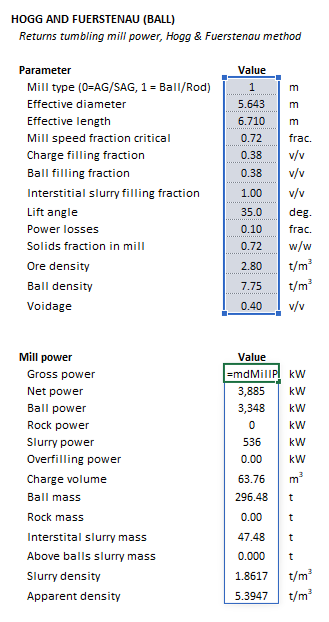
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

Parameters={\begin{bmatrix}{\text{Mill type}}\\D{\text{ (m)}}\\L{\text{ (m)}}\\N_{\rm {c}}{\text{ (frac)}}\\J{\text{ (v/v)}}\\J_{\rm {b}}{\text{ (v/v)}}\\J_{\rm {p}}{\text{ (v/v)}}\\\alpha {\text{ (deg.)}}\\(1-\eta ){\text{ (kW/kW)}}\\f_{\rm {s}}{\text{ (w/w)}}\\\rho _{\rm {m}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\rho _{\rm {b}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\f_{\rm {v}}{\text{ (v/v)}}\\\end{bmatrix}},\;\;\;\;\;\;mdMillPower\_HoggFuerstenau={\begin{bmatrix}P_{\rm {gross}}{\text{ (kw)}}\\P_{\rm {net}}{\text{ (kw)}}\\P_{\rm {b}}{\text{ (kw)}}\\P_{\rm {r}}{\text{ (kw)}}\\P_{\rm {s}}{\text{ (kw)}}\\P_{\rm {o}}{\text{ (kw)}}\\{\text{Charge volume (m}}^{\text{3}}{\text{)}}\\{\text{Ball mass (t)}}\\{\text{Rock mass (t)}}\\{\text{Interstital slurry mass (t)}}\\{\text{Above balls slurry mass (t)}}\\\rho _{\rm {p}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\rho _{\rm {ap}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\end{bmatrix}}\;\;\;\;\;\;\;\;\;\;\;\;

where:

${\text{Mill type}}$ is the type of mill, 0 = autogenous or semi-autogenous, 1 = ball
${\text{Charge volume}}$ is the volume of the charge (m³)
${\text{Ball mass}}$ is the mass of balls in the mill (t)
${\text{Rock mass}}$ is the mass of rocks in the mill (t)
${\text{Interstitial slurry mass}}$ is the mass of slurry in the interstitial charge void space (t)
${\text{Above slurry mass}}$ is the mass of excess slurry above the charge (t)

Figure 2. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

Please note the Excel function expects the mill diameter ( $D$ ) and length ( $L$ ) values in units of meters, which are internally converted to feet for use in the power equation presented above.

SysCAD

The Hogg and Fuerstenau power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
HoggFuerstenau
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
MillType	AG/SAG or Ball/Rod	Type of mill, AG/SAG (RockMass, no AboveBallsSLMass) or Ball (AboveBallsSLMass, no RockMass).
MillDiameter	Input/Display	Diameter of the mill (inside liners).
MillLength	Input/Display	Length of the mill (inside liners).
FracCS	Input/Display	Fraction critical speed of the mill.
ChargeFilling	Input/Display	Volumetric fraction of the mill filled with charge, including balls and interstitial voids between balls.
BallFilling	Input/Display	Volumetric fraction of the mill filled with balls, including slurry and interstitial voids between balls.
InterstialSLFill	Input/Display	Volumetric fraction of the interstitial charge void space occupied by slurry.
LiftAngle	Input	Lift angle of the charge.
PowerLosses	Input	Fraction of power lost due to mill drive efficiency ( $=1-\eta$ ).
SolidsFraction	Display	Mass fraction of solids in the slurry phase.
OreDensity	Display	Density of solids.
BallDensity	Input/Display	Density of balls.
Voidage	Input/Display	Volumetric fraction of interstitial void space in the charge
ChargeVolume	Display	Volume of charge in the mill.
BallMass	Display	Mass of balls in the mill.
RockMass	Display	Mass of coarse rocks in the mill (AG/SAG only).
InterstitialSLMass	Display	Mass of slurry occupying charge void space.
AboveBallsSLMass	Display	Mass of excess slurry resident outside/above charge (Ball mill only).
RhoSlurry	Display	Density of slurry phase.
ApparentDensity	Display	Density of total charge (including balls, rock, slurry and voids).
BallsPower	Display	Power drawn by the ball component of the mill load.
RocksPower	Display	Power drawn by the rock component of the mill load.
SlurryPower	Display	Power drawn by the interstitial slurry component of the mill load.
OverfillingPower	Display	Power drawn by the overfilling, or excess, slurry component of the mill load (when the interstitial voids are completely filled with slurry).
NetPower	Display	Net power drawn by the mill (excluding drive inefficiencies).
GrossPower	Display	Gross power drawn by the mill (including drive inefficiencies).

References

↑ Hogg, R., 1972. Power relationships for tumbling mills. AIME Trans., 252, pp.418-423.
↑ Sepúlveda, J.E., 2001. A phenomenological model of semiautogenous grinding processes in a Moly-Cop Tools environment. In Proceedings of SAG (Vol. 4, pp. 301-315).

[Hogg_(1972)-1] Hogg, R., 1972. Power relationships for tumbling mills. AIME Trans., 252, pp.418-423.

[Sepulveda_(2001)-2] Sepúlveda, J.E., 2001. A phenomenological model of semiautogenous grinding processes in a Moly-Cop Tools environment. In Proceedings of SAG (Vol. 4, pp. 301-315).

[1]

[2]

@@ Line 9: / Line 9: @@
 The Hogg and Fuerstenau method adopts the simplified charge geometry shown in Figure 1, and computes mill power as:{{Sepulveda_(2001)}}
-:<math>P_{net}=\eta P_{gross} = 0.238D^{3.5} \left (\frac{L}{D} \right ) N_c \rho_{ap} (J - 1.065J^2)sin \alpha</math>
+:<math>P_{\rm net}=\eta P_{\rm gross} = 0.238D^{3.5} \left (\frac{L}{D} \right ) N_{\rm c} \rho_{\rm ap} (J - 1.065J^2)sin \alpha</math>
 where:
-* <math>P_{net}</math> is the net power draw of the mill, i.e. excluding mill drive losses (kW)
+* <math>P_{\rm net}</math> is the net power draw of the mill, i.e. excluding mill drive losses (kW)
-* <math>P_{gross}</math> is the gross power draw of the mill, i.e. including mill drive losses (kW)
+* <math>P_{\rm gross}</math> is the gross power draw of the mill, i.e. including mill drive losses (kW)
 * <math>\eta</math> is the mill drive efficiency (kW/kW)
 * <math>D</math> is mill diameter (ft)
 * <math>L</math> is mill length (ft)
-* <math>N_c</math> is mill [[Tumbling Mill (Speed)|fraction critical speed]] (frac)
+* <math>N_{\rm c}</math> is mill [[Tumbling Mill (Speed)|fraction critical speed]] (frac)
-* <math>\rho_{ap}</math> is the apparent density of the mill charge (t/m<sup>3</sup>)
+* <math>\rho_{\rm ap}</math> is the apparent density of the mill charge (t/m<sup>3</sup>)
 * <math>J</math> is the volumetric fraction of the mill filled with charge, including balls and interstitial voids between balls (v/v)
 * <math>\alpha</math> is the charge lift angle (degrees)
-The apparent charge density, <math>\rho_{ap}</math>, may be computed as:
+The apparent charge density, <math>\rho_{\rm ap}</math>, may be computed as:
 :<math>
-\rho_{ap} =
+\rho_{\rm ap} =
 \begin{cases}
-\dfrac{(1-f_v) \rho_bJ_b + (1-f_v) \rho_m (J - J_b) + \rho_p J_p f_v J}{J} & \text{for autogenous or semi-autogenous mills}\\
+\dfrac{(1-f_{\rm v}) \rho_{\rm b}J_{\rm b} + (1-f_{\rm v}) \rho_{\rm m} (J - J_{\rm b}) + \rho_{\rm p} J_{\rm p} f_{\rm v} J}{J} & \text{for autogenous or semi-autogenous mills}\\
-\dfrac{(1-f_v) \rho_bJ_b + \rho_pJ_pf_vJ_b + \rho_p(J-J_b)}{J} & \text{for ball mills}
+\dfrac{(1-f_{\rm v}) \rho_{\rm b}J_{\rm b} + \rho_{\rm p}J_{\rm p}f_{\rm v}J_{\rm b} + \rho_{\rm p}(J-J_{\rm b})}{J} & \text{for ball or rod mills}
 \end{cases}
 </math>
 where:
-* <math>f_v</math> is the volumetric fraction of interstitial void space in the charge (usually 0.4) (v/v)
+* <math>f_{\rm v}</math> is the volumetric fraction of interstitial void space in the charge (usually 0.4) (v/v)
-* <math>\rho_b</math> is the density of balls (t/m<sup>3</sup>)
+* <math>\rho_{\rm b}</math> is the density of balls (t/m<sup>3</sup>)
-* <math>\rho_m</math> is the density of solid ore particles (t/m<sup>3</sup>)
+* <math>\rho_{\rm m}</math> is the density of solid ore particles (t/m<sup>3</sup>)
-* <math>\rho_p</math> is the density of slurry (t/m<sup>3</sup>)
+* <math>\rho_{\rm p}</math> is the density of slurry (t/m<sup>3</sup>)
-* <math>J_b</math> is the volumetric fraction of the mill filled with balls, including slurry and interstitial voids between balls (v/v)
+* <math>J_{\rm b}</math> is the volumetric fraction of the mill filled with balls, including slurry and interstitial voids between balls (v/v)
-* <math>J_p</math> is the volumetric fraction of the interstitial charge void space occupied by slurry (v/v)
+* <math>J_{\rm p}</math> is the volumetric fraction of the interstitial charge void space occupied by slurry (v/v)
-Slurry density, <math>\rho_{p}</math>, may be computed as:
+Slurry density, <math>\rho_{\rm p}</math>, may be computed as:
-:<math>\rho_{p} = \frac{1}{\frac{f_s}{\rho_m} + (1-f_s)}</math>
+:<math>\rho_{\rm p} = \dfrac{1}{\dfrac{f_{\rm s}}{\rho_{\rm m}} + (1-f_{\rm s})}</math>
-where <math>f_s</math> is the mass fraction of solids in the slurry (w/w).
+where <math>f_{\rm s}</math> is the mass fraction of solids in the slurry (w/w).
-The net power draw, <math>P_{net}</math>, may be separated into its contributing constituents:
+The net power draw, <math>P_{\rm net}</math>, may be separated into its contributing constituents:
-:<math>P_b=\left ( \frac{(1-f_v) \rho_bJ_b }{\rho_{ap}J} \right ) \cdot P_{net}</math>
+:<math>P_{\rm b}=\left ( \frac{(1-f_{\rm v}) \rho_{\rm b} J_{\rm b} }{\rho_{\rm ap}J} \right ) \cdot P_{\rm net}</math>
-:<math>P_r=\left ( \frac{(1-f_v) \rho_m (J - J_b)}{\rho_{ap}J} \right ) \cdot P_{net}</math>
+:<math>P_{\rm r}=\left ( \frac{(1-f_{\rm v}) \rho_{\rm m} (J - J_{\rm b})}{\rho_{\rm ap}J} \right ) \cdot P_{\rm net}</math>
-:<math>P_s=\left ( \frac{\rho_bJ_pf_vJ_b }{\rho_{ap}J} \cdot  \right ) \cdot P_{net}</math>
+:<math>P_{\rm s}=\left ( \frac{\rho_{\rm p} J_{\rm p}f_{\rm v} J_{\rm b} }{\rho_{\rm ap}J} \cdot  \right ) \cdot P_{\rm net}</math>
-:<math>P_o=\left ( \frac{\rho_p(J-J_b)}{\rho_{ap}J} \cdot  \right ) \cdot P_{net}</math>
+:<math>P_{\rm o}=\left ( \frac{\rho_{\rm p} (J - J_{\rm b})}{\rho_{\rm ap}J} \cdot  \right ) \cdot P_{\rm net}</math>
 where:
-* <math>P_b</math> is the power drawn by the ball component of the mill load (kW)
+* <math>P_{\rm b}</math> is the power drawn by the ball component of the mill load (kW)
-* <math>P_b</math> is the power drawn by the rock (coarse ore) component of the mill load (kW). Autogenous and semi-autogenous mills only.
+* <math>P_{\rm r}</math> is the power drawn by the rock (coarse ore) component of the mill load (kW). Autogenous and semi-autogenous mills only.
-* <math>P_s</math> is the power drawn by the interstitial slurry component of the mill load (kW)
+* <math>P_{\rm s}</math> is the power drawn by the interstitial slurry component of the mill load (kW)
-* <math>P_o</math> is the power drawn by the overfilling, or excess, slurry component of the mill load (when the interstitial voids are completely filled with slurry (kW). Ball mills only.
+* <math>P_{\rm o}</math> is the power drawn by the overfilling, or excess, slurry component of the mill load (when the interstitial voids are completely filled with slurry (kW). Ball mills only.
+<!--
 == Additional notes==
@@ Line 77: / Line 78: @@
 Lift angle may alternatively be employed as a 'fitting parameter' for existing power draw measurements and subsequently used to predict power draw under differing conditions, at the user's discretion.
+-->
 == Excel ==
@@ Line 96: / Line 98: @@
 D\text{ (m)}\\
 L\text{ (m)}\\
-N_c\text{ (frac)}\\
+N_{\rm c}\text{ (frac)}\\
 J\text{ (v/v)}\\
-J_b\text{ (v/v)}\\
+J_{\rm b}\text{ (v/v)}\\
-J_p\text{ (v/v)}\\
+J_{\rm p}\text{ (v/v)}\\
 \alpha\text{ (deg.)}\\
 (1-\eta)\text{ (kW/kW)}\\
-f_s\text{ (w/w)}\\
+f_{\rm s}\text{ (w/w)}\\
-\rho_m\text{ (t/m}^{\text{3}}\text{)}\\
+\rho_{\rm m}\text{ (t/m}^{\text{3}}\text{)}\\
-\rho_b\text{ (t/m}^{\text{3}}\text{)}\\
+\rho_{\rm b}\text{ (t/m}^{\text{3}}\text{)}\\
+f_{\rm v}\text{ (v/v)}\\
 \end{bmatrix},\;\;\;\;\;\;
 mdMillPower\_HoggFuerstenau=
 \begin{bmatrix}
-P_{gross}\text{ (kw)}\\
+P_{\rm gross}\text{ (kw)}\\
-P_{net}\text{ (kw)}\\
+P_{\rm net}\text{ (kw)}\\
-P_b\text{ (kw)}\\
+P_{\rm b}\text{ (kw)}\\
-P_r\text{ (kw)}\\
+P_{\rm r}\text{ (kw)}\\
-P_s\text{ (kw)}\\
+P_{\rm s}\text{ (kw)}\\
-P_o\text{ (kw)}\\
+P_{\rm o}\text{ (kw)}\\
 \text{Charge volume (m}^{\text{3}}\text{)}\\
 \text{Ball mass (t)}\\
@@ Line 120: / Line 123: @@
 \text{Interstital slurry mass (t)}\\
 \text{Above balls slurry mass (t)}\\
-\rho_p\text{ (t/m}^{\text{3}}\text{)}\\
+\rho_{\rm p}\text{ (t/m}^{\text{3}}\text{)}\\
-\rho_{app}\text{ (t/m}^{\text{3}}\text{)}\\
+\rho_{\rm ap}\text{ (t/m}^{\text{3}}\text{)}\\
 \end{bmatrix}\;\;\;\;\;\;\;\;\;\;\;\;
 </math>
@@ Line 151: / Line 154: @@
 |-
 |MillType
-|style="background: #eaecf0" | AG/SAG or Ball
+|style="background: #eaecf0" | AG/SAG or Ball/Rod
 |Type of mill, AG/SAG (''RockMass'', no ''AboveBallsSLMass'') or Ball (''AboveBallsSLMass'', no ''RockMass'').
 |-
@@ Line 197: / Line 200: @@
 |style="background: #eaecf0" | Input/Display
 |Density of balls.
+|-
+|Voidage
+|style="background: #eaecf0" | Input/Display
+|Volumetric fraction of interstitial void space in the charge
 |-
 |ChargeVolume

Tumbling Mill (Power, Hogg and Fuerstenau): Difference between revisions

Latest revision as of 08:31, 26 March 2023

Contents

Description

Model theory

Excel

SysCAD

See also

References

Navigation menu

Tumbling Mill (Power, Hogg and Fuerstenau): Difference between revisions

Latest revision as of 08:31, 26 March 2023

Description

Model theory

Excel

SysCAD

See also

References

Navigation menu

Search