Hydrocyclone (Narasimha-Mainza): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
md>Scott.Munro
 
imported>Scott.Munro
 
(17 intermediate revisions by 3 users not shown)
Line 3: Line 3:
This article describes the '''Narasimha-Mainza''' model for hydrocyclone size classification.
This article describes the '''Narasimha-Mainza''' model for hydrocyclone size classification.


Narasimha's original dissertation describes an empirical hydrocyclone model that improves on the [[Hydrocyclone (Plitt)|Plitt]] and [[Hydrocyclone (Nageswararao)|Nageswararao]] approaches with the addition of several features:{{Narasimha (2009)}}
Narasimha et al. (2014a) describe an empirical hydrocyclone model that improves on the [[Hydrocyclone (Plitt)|Plitt]] and [[Hydrocyclone (Nageswararao)|Nageswararao]] approaches with the addition of several features:{{Narasimha et al. (2014a)}}
* A sharpness of separation equation
* A sharpness of separation equation
* A slurry viscosity term that includes the effects of very fine particles
* A slurry viscosity term that includes the effects of very fine particles
* Terms for cyclone inclination, particle density, g-forces, flow regime (Reynolds Number) and turbulent diffusion
* Terms for cyclone inclination, particle density, g-forces, flow regime (Reynolds Number) and turbulent diffusion


Narasimha et al. (2014) later published a version of the same model based on a larger data set, with the chief difference being in the exponents fitted to the dimensionless groups.{{Narasimha et al. (2014)}}
Narasimha et al. (2014b) subsequently presented a ''multi-component'' version of the same model, with revised equations for cut size and sharpness of separation per ore component:{{Narasimha et al. (2014b)}}
 
Both equation sets are outlined below, and are available for simulation. The 2009 equations are retained for backwards compatibility with other implementations based on the dissertation model.
 
It may, however, be reasonable to assume the 2014 equations are a better choice for simulation, being based on additional data and review since 2009.


== Model theory ==
== Model theory ==


[[File:HydrocycloneNarasimhaMainza1.png|thumb|375px|Figure 1. The dimensions of a hydrocyclone required by the Narasimha-Mainza model.]]
[[File:HydrocycloneNarasimhaMainza1.png|thumb|375px|Figure 1. The dimensions of a hydrocyclone required by the Narasimha-Mainza model.]]
The empirical model equations for both the Narasimha (2009) and Narasimha et al. (2014) models, collectively described as the Narasimha-Mainza model, are outlined below.


The Narasima-Mainza model comprises an equation for the efficiency curve (partition to overflow) and several sub-equations that describe its parameters:
The Narasima-Mainza model comprises an equation for the efficiency curve (partition to overflow) and several sub-equations that describe its parameters:
Line 26: Line 20:


In addition, a relationship between throughput and operating pressure is presented.
In addition, a relationship between throughput and operating pressure is presented.
Several of the equations have been modified from their original printed forms for clarity of comparison.


=== Efficiency curve ===
=== Efficiency curve ===


The Narasimha-Mainza model applies the [[Partitions|Whiten-Beta efficiency curve]] to partition particles to the overflow stream:
The Narasimha-Mainza model applies the [[Partition (Size, Whiten-Beta)|Whiten-Beta efficiency curve]] to partition particles to the overflow stream:


{{Model theory (Text, Whiten-Beta Efficiency Curve)}}
{{Model theory (Text, Whiten-Beta Efficiency Curve)}}
Line 37: Line 29:
=== Corrected cut size ===
=== Corrected cut size ===


The corrected cut size, <math>d_{50c}</math> (m), is computed from:
The corrected cut size, <math>d_{\rm 50c}</math> (m), is computed from:


:<math>
:<math>
\begin{cases}
\dfrac {d_{\rm 50c}}{D_{\rm c}} = K_{\rm d0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{1.093} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.936} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{-0.217}
\dfrac {d_{50c}}{D_c} = K_{d0} {\left( \dfrac {D_o}{D_c} \right)}^{1.207} {\left( \dfrac {D_u}{D_c} \right)}^{-0.921} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.657} (\text{Re})^{-0.500} {\left( \dfrac {D_i}{D_c} \right)}^{-0.750} {\left( \dfrac {L_c}{D_c} \right)}^{0.272} {\left( \dfrac {\tan \theta}{2} \right)}^{0.139}\phantom{00} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{-1.050} {\left( \dfrac {\rho_s - \rho_f}{\rho_f} \right)}^{-0.244} & \text{Narasimha (2009)}\\
\\
\dfrac {d_{50c}} {D_c} = K_{d0} {\left( \dfrac {D_o} {D_c} \right)}^{1.093} {\left( \dfrac {D_u} {D_c} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_i} {D_c} \right)}^{-0.936} {\left( \dfrac {L_c} {D_c} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_s - \rho_f}{\rho_f} \right)}^{-0.217} & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
</math>


where:
where:
* <math>K_{d0}</math> is a calibration factor which should be fitted to operating data
* <math>K_{\rm d0}</math> is a calibration factor which should be fitted to operating data
* <math>D_c</math> is diameter of the cyclone (m)
* <math>D_{\rm c}</math> is diameter of the cyclone (m)
* <math>D_i</math> is diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet (m)
* <math>D_{\rm i}</math> is diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet (m)
* <math>D_o</math> is diameter of the vortex finder (overflow) (m)
* <math>D_{\rm o}</math> is diameter of the vortex finder (overflow) (m)
* <math>D_u</math> is diameter of the apex/spigot (underflow) (m)
* <math>D_{\rm u}</math> is diameter of the apex/spigot (underflow) (m)
* <math>L_c</math> is length of the cylindrical section (m)
* <math>L_{\rm c}</math> is length of the cylindrical section (m)
* <math>\theta</math> is the cone full angle (deg.)
* <math>\theta</math> is the cone full angle (deg.)
* <math>i</math> is the angle of inclination from the vertical (rad)
* <math>i</math> is the angle of inclination from the vertical (rad)
* <math>f_v</math> is the volume fraction of solids in the feed (v/v)
* <math>f_{\rm v}</math> is the volume fraction of solids in the feed (v/v)
* <math>\rho_s</math> is the density of solids in the feed (t/m<sup>3</sup>)
* <math>\rho_{\rm s}</math> is the density of solids in the feed (t/m<sup>3</sup>)
* <math>\rho_f</math> is the density of the fluid (liquids) in the feed (t/m<sup>3</sup>)
* <math>\rho_{\rm f}</math> is the density of the fluid (liquids) in the feed (t/m<sup>3</sup>)
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>)
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>)


The Reynolds Number, <math>Re</math>, is:
The Reynolds Number, <math>\rm Re</math>, is:


:<math>Re  = \dfrac{1000 V_i D_c \rho_p}{0.001\mu_r}</math>
:<math>{\rm Re} = \dfrac{1000 V_i D_{\rm c} \rho_{\rm p}}{0.001\mu_{\rm r}}</math>


The feed inlet velocity, <math>V_i</math> (m/s), is:
The feed inlet velocity, <math>V_i</math> (m/s), is:


:<math>V_i = \dfrac{Q_f}{\dfrac{\pi}{4}{D_i}^2}</math>
:<math>V_i = \dfrac{Q_{\rm f}}{\dfrac{\pi}{4}{D_{\rm i}}^2}</math>


where <math>Q_f</math> is the volumetric feed flow rate (m<sup>3</sup>/h), and <math>\rho_p</math> is the density of the feed pulp (t/m<sup>3</sup>).
where <math>Q_{\rm f}</math> is the volumetric feed flow rate (m<sup>3</sup>/h), and <math>\rho_{\rm p}</math> is the density of the feed pulp (t/m<sup>3</sup>).


The relative slurry viscosity, <math>\mu_r</math>, is the ratio of slurry and water viscosities, <math>\mu_m</math> and <math>\mu_w</math>, which is approximated by:
The relative slurry viscosity, <math>\mu_{\rm r}</math>, is the ratio of slurry and water viscosities, <math>\mu_{\rm m}</math> and <math>\mu_{\rm w}</math>, which is approximated by:


:<math>\mu_r = \dfrac{\mu_m}{\mu_w} = \left ( 1 - \dfrac{f_v}{0.622} \right)^{-1.55} ({F_{-38\mu}})^{0.39}</math>
:<math>\mu_{\rm r} = \dfrac{\mu_{\rm m}}{\mu_{\rm w}} = \left ( 1 - \dfrac{f_{\rm v}}{0.622} \right)^{-1.55} ({F_{-38\mu}})^{0.39}</math>


where <math>F_{-38\mu}</math> is the cumulative fraction passing 38 μm in the feed (frac).
where <math>F_{-38\mu}</math> is the cumulative fraction passing 38 μm in the feed (frac).
Line 79: Line 67:
=== Liquids recovery ===
=== Liquids recovery ===


The fraction of feed liquid recovered to the underflow stream, <math>R_f</math>, is related to <math>C</math> (i.e. <math>C = 1 - R_f</math>), and is computed as:
The fraction of feed liquid recovered to the underflow stream, <math>R_{\rm f}</math>, is related to <math>C</math> (i.e. <math>C = 1 - R_{\rm f}</math>), and is computed as:


:<math>
:<math>
R_f =
R_{\rm f} = K_{\rm w0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{-1.06787} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{2.2062} {\left( \dfrac {V^2_t} {R_{\rm max}g} \right)}^{-0.20472} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{-0.829} {\mu_{\rm r}}^{-0.7118} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{2.424} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.8843} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}} {\rho_{\rm f}} \right)}^{0.523} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.793}
\begin{cases}
K_{w0} {\left( \dfrac {D_o} {D_c} \right)}^{-0.835\phantom{00}} {\left( \dfrac {D_u} {D_c} \right)}^{2.190\phantom{0}} {\left( \dfrac {V^2_t} {R_{max}g} \right)}^{-0.259\phantom{00}} {\left( {\tan \left( \dfrac{\theta}{2}\right)}  \right)}^{-0.649} {\mu_r}^{-0.792\phantom{0}} {\left( \dfrac {L_c} {D_c} \right)}^{1.937} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.930} {\left( \dfrac {\rho_s - \rho_f} {\rho_f} \right)}^{0.462} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.765} & \text{Narasimha (2009)}\\
\\
K_{w0} {\left( \dfrac {D_o} {D_c} \right)}^{-1.06787} {\left( \dfrac {D_u} {D_c} \right)}^{2.2062} {\left( \dfrac {V^2_t} {R_{max}g} \right)}^{-0.20472} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{-0.829} {\mu_r}^{-0.7118} {\left( \dfrac {L_c} {D_c} \right)}^{2.424} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.8843} {\left( \dfrac {\rho_s - \rho_f} {\rho_f} \right)}^{0.523} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.793} & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
</math>


where <math>K_{w0}</math> is a calibration factor which should be fitted to operating data.
where <math>K_{\rm w0}</math> is a calibration factor which should be fitted to operating data.


<math>R_{max}</math> is the radius of the cyclone (m), i.e.:
<math>R_{\rm max}</math> is the radius of the cyclone (m), i.e.:


:<math>R_{max} = 0.5 D_c</math>
:<math>R_{\rm max} = 0.5 D_{\rm c}</math>


and the tangential velocity, <math>V_t</math> (m/s), is:
and the tangential velocity, <math>V_{\rm t}</math> (m/s), is:


:<math>V_t = 4.5 V_i \left ( \dfrac{D_i}{D_c} \right )^{1.13}</math>
:<math>V_{\rm t} = 4.5 V_i \left ( \dfrac{D_{\rm i}}{D_{\rm c}} \right )^{1.13}</math>


=== Sharpness of separation ===
=== Sharpness of separation ===
Line 105: Line 88:


:<math>
:<math>
\alpha =
\alpha = K_\alpha {{ {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.567} {\left( \dfrac {\left( \rho_{\rm s} - \rho_{\rm p} \right)} {\rho_{\rm s}} \right)}^{-1.837} {\mu_{\rm r}}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.2}} }}
\begin{cases}
K_\alpha {{\left( \dfrac {D_o} {D_c} \right)}^{0.191} {\left( \dfrac {V_t^2} {gR_{max}} \right)}^{0.012} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.751} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_v}} \right)}^{0.739}} {{\left( \dfrac {D_u} {D_c} \right)}^{-0.467} {\left( \dfrac {\left( \rho_s - \rho_p \right)} {\rho_s} \right)}^{-1.670} {\mu_r}^{-0.112} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.018} {\left( \dfrac {L_c} {D_c} \right)}^{-0.233}} & \text{Narasimha (2009)}\\
\\
K_\alpha {{ {{\left( \dfrac {D_o} {D_c} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_t^2} {gR_{max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_v}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_u} {D_c} \right)}^{-0.567} {\left( \dfrac {\left( \rho_s - \rho_p \right)} {\rho_s} \right)}^{-1.837} {\mu_r}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_c} {D_c} \right)}^{-0.2}} }} & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
</math>


Line 117: Line 95:
=== Cyclone capacity ===
=== Cyclone capacity ===


The volumetric capacity of a cyclone at a given operating pressure, <math>Q</math> (m<sup>3</sup>/h), is estimated from the pressure-throughput relationship:
The '''volumetric capacity''' of a cyclone at a given operating pressure, <math>Q</math> (m<sup>3</sup>/h), is estimated from the pressure-throughput relationship:


:<math>
:<math>
Q =  
Q = K_{\rm Q0} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{0.45} {D_{\rm c}}^{2} \sqrt \dfrac P {\rho_{\rm p}} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{1.099} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.092}
\begin{cases}
K_{Q0} {\left( \dfrac {D_i} {D_c} \right)}^{0.45} {D_c}^{2} \sqrt \dfrac P {\rho_p} {\left( \dfrac {D_o} {D_c} \right)}^{1.250} {\left( \dfrac {D_u} {D_c} \right)}^{0.060} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_c} {D_c} \right)}^{0.330} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.047} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.090} & \text{Narasimha (2009)}\\
\\
K_{Q0} {\left( \dfrac {D_i} {D_c} \right)}^{0.45} {D_c}^{2} \sqrt \dfrac P {\rho_p} {\left( \dfrac {D_o} {d_c} \right)}^{1.099} {\left( \dfrac {D_u} {D_c} \right)}^{0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_c} {D_c} \right)}^{0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{-0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.092} & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
</math>


where <math>K_{Q0}</math> is a calibration factor which should be fitted to operating data, and <math>P</math> is the pressure drop across the operating cyclone (kPa).
where <math>K_{\rm Q0}</math> is a calibration factor which should be fitted to operating data, and <math>P</math> is the pressure drop across the operating cyclone (kPa).


This expression may be used to estimate the number of cyclones required to accept a given total cluster feed flow rate at a fixed pressure, e.g. a process set point.
This expression may be used to estimate the number of cyclones required to accept a given total cluster feed flow rate at a fixed pressure, e.g. a process set point.


Alternatively, the pressure drop arising from a given feed flow rate may be calculated by rearranging the above equation:
Alternatively, the '''pressure drop''' arising from a given feed flow rate may be calculated by rearranging the above equation:


:<math>
:<math>
P =  
P = \rho_{\rm p} \left [ Q {{K_{\rm Q0}}^{-1} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.45} {D_{\rm c}}^{-2} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{-1.099} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.092}} \right ]^2
\begin{cases}
\rho_p \left [ Q {{K_{Q0}}^{-1} {\left( \dfrac {D_i} {D_c} \right)}^{-0.45} {D_c}^{-2} {\left( \dfrac {D_o} {D_c} \right)}^{-1.250} {\left( \dfrac {D_u} {D_c} \right)}^{-0.060} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_c} {D_c} \right)}^{-0.330} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{0.047} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.090}} \right ]^2 & \text{Narasimha (2009)}\\
\\
\rho_p \left [ Q {{K_{Q0}}^{-1} {\left( \dfrac {D_i} {D_c} \right)}^{-0.45} {D_c}^{-2} {\left( \dfrac {D_o} {d_c} \right)}^{-1.099} {\left( \dfrac {D_u} {D_c} \right)}^{-0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_c} {D_c} \right)}^{-0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_v \right)}^2} {10^{1.82f_v}} \right)}^{0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.092}} \right ]^2 & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
</math>


=== Multi-component modelling ===
=== Multi-component modelling ===


The original 2009 and 2014 Narasimha-Mainza model formulations only consider the classification of a single ore component with a density <math>\rho_s</math>.
==== Narasimha, Mainza and Holtham (2014) ====
 
The Narasimha-Mainza model formulation only considers the classification of solid particles with a single average feed density, <math>\rho_{\rm s}</math>.
 
Narasimha et al. (2014b) explored the classification of ''multi-component'' feeds, deriving modified equations for cut size and sharpness of separation per ore component:{{Narasimha et al. (2014b)}}
 
:<math>
\dfrac {(d_{\rm 50c})_j}{D_{\rm c}} = K_{\rm d0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{1.093} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.936} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_{{\rm s}j} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{-1.37}
</math>
 
and
 
:<math>
\alpha_j = K_\alpha {{ {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.567} {\left(  \rho_{{\rm s}j} - \rho_{\rm p}  \right)}^{-0.983} {\mu_{\rm r}}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.2}} }}
</math>
 
where <math>\rho_{{\rm s}j}</math> is the density of solid ore component <math>j</math> (t/m<sup>3</sup>).
 
A multi-component version of the Narasimha-Mainza model is available which replaces the average density cut size and sharpness of separation equations with their per ore equivalents above. The multi-component version is named as '''Narasimha-Mainza (Multi)''' to distinguish it from the primary Narasimha-Mainza (2014) formulation.
 
==== Silveira, Delboni and Bergerman (2024) ====
 
More recently, Silveira et al. (2024) simulated multicomponent classification with the Narasimha-Mainza model by assigning separate cut size and sharpness coefficients to the valuable mineral phase and overall ore partitions.{{Silveira et al. (2024)}}


This implementation allows a user to specify different densities for each ore type in the feed. An efficiency curve is then generated for each ore using individual density values in place of <math>\rho_s</math> in the above equations.
This concept is extended here to allow the specification of cut size and sharpness coefficients for each ore/mineral/class type in the feed, i.e. <math>(K_{\rm d0})_j</math> and <math>(K_{\alpha 0})_j</math> replacing <math>K_{\rm d0}</math> and <math>K_{\alpha 0}</math>.


=== Partition metrics ===
=== Partition metrics ===
Line 156: Line 146:


{{Model theory (Text, Hydrocyclone, Roping)}}
{{Model theory (Text, Hydrocyclone, Roping)}}
== Additional notes ==
Note that the equations presented by Narasimhsa  et al. (2014) differ from those presented in Narasimha's original dissertation.{{Narasimha (2009)}}
The user should be aware of which model formulation is being applied when adopting calibration parameters from external sources. Recalibration of model parameters via the Excel interface below is recommended in such cases.


== Excel ==
== Excel ==
Line 161: Line 157:
The Narasimha-Mainza hydrocyclone model may be invoked from the Excel formula bar with the following function call:
The Narasimha-Mainza hydrocyclone model may be invoked from the Excel formula bar with the following function call:


<syntaxhighlight lang="vb">=mdUnit_Hydrocyclone_NarasimhaMainza(Parameters as Range, Size as Range, Feed as Range, OreSG Range)</syntaxhighlight>
<syntaxhighlight lang="vb">=mdUnit_Hydrocyclone_NarasimhaMainza(Parameters as Range, Size as Range, Feed as Range, OreSG Range, Optional Kd0 as Range, Optional Kalpha0 as Range)</syntaxhighlight>


{{Excel (Text, Help, No Arguments)}}
{{Excel (Text, Help, No Arguments)}}
Line 169: Line 165:
{{Excel (Text, Inputs)}}
{{Excel (Text, Inputs)}}


:<math>Parameters=
:<math>\mathit{Parameters}=
\begin{bmatrix}
\begin{bmatrix}
\text{Method}\\
\text{Method}\\
\text{Pressure control}\\
\text{Pressure control}\\
\text{Number of cyclones}\\
\text{Number of cyclones}\\
D_c\text{ (m)}\\
D_{\rm c}\text{ (m)}\\
D_i\text{ (m)}\\
D_{\rm i}\text{ (m)}\\
D_o\text{ (m)}\\
D_{\rm o}\text{ (m)}\\
D_u\text{ (m)}\\
D_{\rm u}\text{ (m)}\\
L_c\text{ (m)}\\
L_{\rm c}\text{ (m)}\\
\theta\text{ (deg.)}\\
\theta\text{ (deg.)}\\
i\text{ (deg.)}\\
i\text{ (deg.)}\\
P\text{ (kPa)}\\
P\text{ (kPa)}\\
K_{d0}\\
K_{\rm d0}\\
K_{Q0}\\
K_{\rm Q0}\\
K_{w0}\\
K_{\rm w0}\\
K_{\alpha}\\
K_{\alpha}\\
\beta\\
\beta\\
Q_m^{Liquids}\text{ (t/h)}\\
(Q_{\rm M,F})_{\rm L}\text{ (t/h)}\\
\rho_f\text{ (t/m}^{\text{3}}\text{)}\\
\rho_{\rm f}\text{ (t/m}^{\text{3}}\text{)}\\
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\quad
 
\begin{array}{l}


Size = \begin{bmatrix}
Size = \begin{bmatrix}
Line 195: Line 193:
\vdots\\  
\vdots\\  
d_n\text{ (mm)}\\  
d_n\text{ (mm)}\\  
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\quad


Feed= \begin{bmatrix}
\mathit{Feed}= \begin{bmatrix}
(Q_m^F)_{11}\text{ (t/h)} & \dots & (Q_m^F)_{1m}\text{ (t/h)}\\  
(Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\  
\vdots & \ddots & \vdots\\  
\vdots & \ddots & \vdots\\  
(Q_m^F)_{n1}\text{ (t/h)} & \dots & (Q_m^F)_{nm}\text{ (t/h)}\\  
(Q_{\rm M,F})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{nm}\text{ (t/h)}\\  
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\quad


OreSG= \begin{bmatrix}
\mathit{OreSG}= \begin{bmatrix}
(\rho_s)_1\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_s)_m\text{ (t/m}^\text{3}\text{)}\\  
(\rho_{\rm s})_1\text{ (t/m}^\text{3}\text{)} & \dots & (\rho_{\rm s})_m\text{ (t/m}^\text{3}\text{)}\\  
\end{bmatrix}
\end{bmatrix},\quad
 
\mathit{Kd0}= \begin{bmatrix}
(K_{\rm d0})_1 & \dots & (K_{\rm d0})_m\\
\end{bmatrix}^*,\quad
 
\mathit{Kalpha 0}= \begin{bmatrix}
(K_{\alpha 0})_1 & \dots & (K_{\alpha 0})_m\\
\end{bmatrix}^*


\end{array}
</math>
</math>




where:
where:
* <math>\text{Method}</math> is the set of equations to use (''0 = Narasimha (2009), 1 = Narasimha et al. (2014)'')
* <math>\text{Method}</math> is the set of equations to use (''0 = Narasimha et al. (2014), 1 = Narasimha et al. (Multi)'')
* <math>\text{Pressure control}</math> indicates whether the number of cyclones required at the given feed flow rate and pressure set point is returned (''TRUE'') or the operating pressure at the given feed flowrate and number of cyclones is returned (''FALSE'')
* <math>\text{Pressure control}</math> indicates whether the number of cyclones required at the given feed flow rate and pressure set point is returned (''TRUE'') or the operating pressure at the given feed flowrate and number of cyclones is returned (''FALSE'')
* <math>\text{Number of cyclones}</math> is the number of cyclones ''operating'' in a cluster. The number of cyclones is ignored if <math>\text{Pressure control}</math> is ''TRUE'' (the value is returned in the results instead)
* <math>\text{Number of cyclones}</math> is the number of cyclones ''operating'' in a cluster. The number of cyclones is ignored if <math>\text{Pressure control}</math> is ''TRUE'' (the value is returned in the results instead)
* <math>P</math>, the operating pressure, is ignored if <math>\text{Pressure control}</math> is ''FALSE'' (the value is returned in the results instead)
* <math>P</math>, the operating pressure, is ignored if <math>\text{Pressure control}</math> is ''FALSE'' (the value is returned in the results instead)
* <math>\rho_f</math> is the density of liquids (fluids) in the feed (t/m<sup>3</sup>)
* <math>\rho_{\rm f}</math> is the density of liquids (fluids) in the feed (t/m<sup>3</sup>)
* <math>d_i</math> is the size of the square mesh interval that feed mass is retained on (mm)
* <math>m</math> is the number of ore types
* <math>m</math> is the number of ore types
* <math>Q_m^F</math> is feed solids mass flow rate by size and ore type (t/h)
* <math>Q_{\rm M,F}</math> is feed solids mass flow rate by size and ore type (t/h)
* <math>Q_m^{Liquids}</math> is the mass flow feed rate of liquids into the cyclone (t/h)
* <math>(Q_{\rm M,F})_{\rm L}</math> is the mass flow feed rate of liquids into the cyclone (t/h)
* <math>^*</math> indicates optional arrays to specify cut size and sharpness parameters by ore/mineral/class type. If either array is omitted (default), the <math>K_{{\rm d0}}</math> and <math>K_{\alpha 0}</math>values supplied in the <math>\mathit{Parameters}</math> array are used instead.


=== Results ===
=== Results ===
Line 225: Line 234:


:<math>
:<math>
mdUnit\_Hydrocyclone\_NarasimhaMainza =  
\mathit{mdUnit\_Hydrocyclone\_NarasimhaMainza} =  
\begin{bmatrix}
\begin{bmatrix}


\begin{array}{c}
\begin{bmatrix}
\text{Number of cyclones}\\
\text{Number of cyclones}\\
\text{Qv per cyclone (m}^{\text{3}}\text{/h)}\\
\text{Qv per cyclone (m}^{\text{3}}\text{/h)}\\
\text{Qv per cluster (m}^{\text{3}}\text{/h)}\\
\text{Qv per cluster (m}^{\text{3}}\text{/h)}\\
C_V \text{ (}\%\text{ v/v)}\\
C_{\rm V} \text{ (}\%\text{ v/v)}\\
P\text{ (kPa)}\\
P\text{ (kPa)}\\
R_v\text{ (frac)}\\
R_{\rm v}\text{ (frac)}\\
R_f\text{ (frac)}\\
R_{\rm f}\text{ (frac)}\\
\text{Water split to OF (frac)}\\
\text{Water split to OF (frac)}\\
d_{50c}\text{ (mm)}\\
d_{\rm 50c}\text{ (mm)}\\
Q_m^{LiqOF}\text{ (t/h)}\\
(Q_{\rm M,OF})_{\rm L}\text{ (t/h)}\\
Q_m^{LiqUF}\text{ (t/h)}\\
(Q_{\rm M,UF})_{\rm L}\text{ (t/h)}\\
d_{50}\text{ (mm)}\\
d_{50}\text{ (mm)}\\
E_p\text{ (mm)}\\
E_{\rm p}\text{ (mm)}\\
I\\
I\\
\text{SPOC }C_{VU}\text{ (v/v)}\\
\text{SPOC }C_{\rm VU}\text{ (v/v)}\\
\text{Plitt }M_{SU}\text{ (m}^{3}\text{/h)}\\
\text{Plitt }M_{\rm SU}\text{ (m}^{3}\text{/h)}\\
\text{Plitt }\Phi_L\text{ (v/v)}\\
\text{Plitt }\Phi_{\rm L}\text{ (v/v)}\\
\text{Bustamante condition}\\
\text{Bustamante condition}\\
\text{Concha condition}\\
\text{Concha condition}\\
\end{array}
\end{bmatrix}




Line 263: Line 272:


\begin{bmatrix}
\begin{bmatrix}
Q^{UF}_{11}\text{ (t/h)} & \dots & Q^{UF}_{1m}\text{ (t/h)}\\
(Q_{\rm M,UF})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,UF})_{1m}\text{ (t/h)}\\
\vdots & \ddots & \vdots\\
(Q_{\rm M,UF})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,UF})_{nm}\text{ (t/h)}\\
\end{bmatrix}
 
&
 
\begin{bmatrix}
(Q_{\rm M,OF})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,OF})_{1m}\text{ (t/h)}\\
\vdots & \ddots & \vdots\\
\vdots & \ddots & \vdots\\
Q^{UF}_{n1}\text{ (t/h)} & \dots & Q^{UF}_{nm}\text{ (t/h)}\\
(Q_{\rm M,OF})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,OF})_{nm}\text{ (t/h)}\\
\end{bmatrix}
\end{bmatrix}


Line 271: Line 288:


\begin{bmatrix}
\begin{bmatrix}
(Q_m^{OF})_{11}\text{ (t/h)} & \dots & (Q_m^{OF})_{1m}\text{ (t/h)}\\
(E_{\rm oa})_{11}\text{ (frac)} & \dots & (E_{\rm oa})_{1m}\text{ (frac)}\\
\vdots & \ddots & \vdots\\
\vdots & \ddots & \vdots\\
(Q_m^{OF})_{n1}\text{ (t/h)} & \dots & (Q_m^{OF})_{nm}\text{ (t/h)}\\
(E_{\rm oa})_{n1}\text{ (frac)} & \dots & (E_{\rm oa})_{nm}\text{ (frac)}\\
\end{bmatrix}
\end{bmatrix}


Line 279: Line 296:


\begin{bmatrix}
\begin{bmatrix}
P^{OF}_1\text{ (mm)}\\
(P_{\rm OF})_{1,{\rm All}}\\
\vdots\\
\vdots\\
P^{OF}_n\text{ (mm)}
(P_{\rm OF})_{n,{\rm All}}\\
\end{bmatrix}
\end{bmatrix}


Line 287: Line 304:


\begin{bmatrix}
\begin{bmatrix}
(d_{50c})_1 & \dots & (d_{50c})_m\\
\alpha_1 & \dots & \alpha_m\\
(d_{\rm 50c})_1 & \dots & (d_{\rm 50c})_m\\
\beta^*_1 & \dots & \beta^*_m\\
\beta^*_1 & \dots & \beta^*_m\\
\end{bmatrix}\\
\end{bmatrix}\\
Line 319: Line 337:
* <math>\text{P}</math> is the pressure drop across the cyclone cluster with <math>\text{Number of cyclones}</math> operating at feed rate <math>\text{Qv per cluster}</math>, if <math>\text{Pressure control}</math> = ''FALSE'' (kPa)
* <math>\text{P}</math> is the pressure drop across the cyclone cluster with <math>\text{Number of cyclones}</math> operating at feed rate <math>\text{Qv per cluster}</math>, if <math>\text{Pressure control}</math> = ''FALSE'' (kPa)
* <math>\text{Water split to OF}</math> is actual split of liquids to the overflow (frac)
* <math>\text{Water split to OF}</math> is actual split of liquids to the overflow (frac)
* <math>Q_m^{LiqOF}</math> is the mass flow rate of liquids to the overflow stream (t/h)
* <math>(Q_{\rm M,OF})_{\rm L}</math> is the mass flow rate of liquids to the overflow stream (t/h)
* <math>Q_m^{LiqUF}</math> is the mass flow rate of liquids to the underflow stream (t/h)
* <math>(Q_{\rm M,UF})_{\rm L}</math> is the mass flow rate of liquids to the underflow stream (t/h)
* <math>Q_m^{UF}</math> is mass flow rate of solids to the underflow stream (t/h)
* <math>\text{SPOC }C_{\rm VU}</math> is the SPOC roping limit of volume fraction solids in the underflow stream (v/v)
* <math>Q_m^{OF}</math> is mass flow rate of solids to the overflow stream (t/h)
* <math>\text{Plitt }M_{\rm SU}</math> is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m<sup>3</sup>/h)
* <math>P^{OF}</math> is partition fraction of feed solids to the overflow stream (frac)
* <math>\text{Plitt }\Phi_{\rm L}</math> is the Plit roping limit of volume fraction solids in the underflow stream (v/v)
* <math>\text{SPOC }C_{VU}</math> is the SPOC roping limit of volume fraction solids in the underflow stream (v/v)
* <math>\text{Plitt }M_{SU}</math> is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m<sup>3</sup>/h)
* <math>\text{Plitt }\Phi_L</math> is the Plit roping limit of volume fraction solids in the underflow stream (v/v)
* <math>\text{Bustamante condition}</math> is the underflow discharge type based on the Bustamante geometry limits (''spray'' or ''roping'' discharge)
* <math>\text{Bustamante condition}</math> is the underflow discharge type based on the Bustamante geometry limits (''spray'' or ''roping'' discharge)
* <math>\text{Concha condition}</math> is the underflow discharge type based on the Concha geometry limits (''spray'' or ''roping'' discharge)
* <math>\text{Concha condition}</math> is the underflow discharge type based on the Concha geometry limits (''spray'' or ''roping'' discharge)
* <math>Q_{\rm M,UF}</math> is mass flow rate of solids to the underflow stream (t/h)
* <math>Q_{\rm M,OF}</math> is mass flow rate of solids to the overflow stream (t/h)
* <math>(P_{\rm OF})_{i,{\rm All}}</math> is the actual partition of all particles of size <math>i</math> to the overflow stream, computed as <math>\frac{\sum_{j=1}^m(Q_{\rm M,OF})_{ij}}{\sum_{j=1}^m(Q_{\rm M,F})_{ij}}</math> (frac)


=== Example ===
=== Example ===
Line 343: Line 361:
The sections and variable names used in the SysCAD interface are described in detail in the following tables.
The sections and variable names used in the SysCAD interface are described in detail in the following tables.


{{SysCAD (Page, Hydrocyclone, ScdMD*Hydrocyclone)}}
{{SysCAD (Page, Hydrocyclone, DLL*Hydrocyclone)}}


==== Cyclone page ====
==== Cyclone page ====
Line 349: Line 367:
The Cyclone page is used to specify the input parameters for the hydrocyclone model.
The Cyclone page is used to specify the input parameters for the hydrocyclone model.


{{SysCAD_Table_Header}}
{{SysCAD (Text, Table Header)}}


|-
|-
! colspan="3" style="text-align:left;" |''NarasimhaMainza''
! colspan="3" style="text-align:left;" |''NarasimhaMainza''
{{SysCAD (Text, Help Link)}}
|-
|-
|PressureControl
|PressureControl
|CheckBox
|CheckBox
|If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate.
|If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate.
|-
|OreSpecific
|CheckBox
|Only appears if the Narasimha-Mazina (2014) model method is selected. If enabled, allows Kd0 and Kalpha parameters to be specified per species.
|-
|-
! colspan="3" style="text-align:left;" |''Dimensions''
! colspan="3" style="text-align:left;" |''Dimensions''
Line 418: Line 443:
|'Fish hook' parameter of the Whiten-Beta efficiency curve equation.
|'Fish hook' parameter of the Whiten-Beta efficiency curve equation.


{{SysCAD (Text, Hydrocyclone, Liquids)}}
{{SysCAD (Text, Hydrocyclone, Liquids)|method=0}}


|-
|-
! colspan="3" style="text-align:left;" |''Results''
! colspan="3" style="text-align:left;" |''Results''
|-
|-
|ClusterQv
|ClusterQv / Cluster.Qv
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Volumetric flow rate of feed to the cyclone cluster (i.e. total flow).
|Volumetric flow rate of feed to the cyclone cluster (i.e. total flow).
|-
|-
|CycloneQv
|CycloneQv / Cyclone.Qv
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow).
|Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow).
|-
|-
|OperatingPressure
|OperatingPressure / P
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Pressure drop across the cyclone.
|Pressure drop across the cyclone.
|-
|-
|fv
|VolFracSolids / fv
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Volume fraction of solids in feed stream.
|Volume fraction of solids in feed stream.
|-
|-
|mur
|RelSlurryVisc / mur
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Relative slurry viscosity.
|Relative slurry viscosity.
Line 463: Line 488:
|}
|}


{{SysCAD (Page, Hydrocyclone, Partition)}}
{{SysCAD (Page, Hydrocyclone, Partition)|ActionU=Partition|ActionL=partition|DestinationU=Overflow|DestinationL=overflow|UnitL=cyclone}}


{{SysCAD (Page, Hydrocyclone, Roping)}}
{{SysCAD (Page, Hydrocyclone, Roping)}}


{{SysCAD (Page, About)}}
{{SysCAD (Page, About)}}
==== Additional notes ====
{{SysCAD (Text, No PSD Splits)|gasstream=overflow}}


== See also ==
== See also ==
Line 478: Line 507:
[[Category:Excel]]
[[Category:Excel]]
[[Category:SysCAD]]
[[Category:SysCAD]]
<!---
=== User equations ===
A version of the Narasimha-Mainza model with user-definable equation exponents is provided. This offers model compatibility with formulations of the equations that may be based on other sources.
The user-defineable equations are:
:<math>
\dfrac {(d_{\rm 50c})_i}{D_{\rm c}} = K_{\rm d0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{d_1} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{d_2} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{d_3} (\text{Re})^{d_4} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{d_5} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{d_6} {\big( \tan (d_7 \theta) \big)}^{d_8} {\left( \cos \left( \dfrac i 2 \right) \right)}^{d_9} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{d_{10}} {\left( \dfrac {\rho_{si} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{d_{11}}
</math>
:<math>
R_{\rm f} = K_{\rm w0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{w_1} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{w_2} {\left( \dfrac {V^2_t} {R_{\rm max}g} \right)}^{w_3} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{w_4} {\mu_{\rm r}}^{w_5} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{w_6} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{w_7} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}} {\rho_{\rm f}} \right)}^{w_8} {\left( \cos \left(\dfrac i 2 \right) \right)}^{w_9}
</math>
:<math>
\alpha_i = K_\alpha {{ {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{\alpha_1} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{\alpha_2} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{\alpha_3} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{\alpha_4}} } { {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{\alpha_5} {\left( \dfrac {\left( \rho_{\rm s} - \rho_{\rm p} \right)} {\rho_{\rm s}} \right)}^{\alpha_6} {\mu_{\rm r}}^{\alpha_7} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{\alpha_8} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{\alpha_9}} }} \left( \rho_{\rm s} - \rho_{\rm p} \right)^{\alpha_{10}}
</math>
:<math>
Q = K_{\rm Q0} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{Q_1} {D_{\rm c}}^{2} \sqrt \dfrac P {\rho_{\rm p}} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{Q_2} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{Q_3} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{Q_4} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{Q_5} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{Q_6} {\left( \cos \left( \dfrac i 2 \right) \right)}^{Q_7}
</math>
:<math>
P = \rho_{\rm p} \left [ Q {{K_{\rm Q0}}^{-1} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-Q_1} {D_{\rm c}}^{-2} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{-Q_2} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-Q_3} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-Q_4} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-Q_5} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-Q_6} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-Q_7}} \right ]^2
</math>
where:
* <math>\rho_{si}</math> is the density of solid (ore) component <math>i</math> (t/m<sup>3</sup>)
* <math>d_1 \dots d_{10}</math> are user-defined exponents of the corrected cut size equation
* <math>w_1 \dots w_9</math> are user-defined exponents of the liquids recovery equation
* <math>\alpha_1 \dots \alpha_9</math> are user-defined exponents of the sharpness of separation equation
* <math>Q_1 \dots Q_9</math> are user-defined exponents of the cyclone capacity equation
:<math>
\dfrac {d_{\rm 50c}}{D_{\rm c}} =
\begin{cases}
K_{\rm d0} {\left( \dfrac {D_{\rm o}}{D_{\rm c}} \right)}^{1.207} {\left( \dfrac {D_{\rm u}}{D_{\rm c}} \right)}^{-0.921} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.657} (\text{Re})^{-0.500} {\left( \dfrac {D_{\rm i}}{D_{\rm c}} \right)}^{-0.750} {\left( \dfrac {L_{\rm c}}{D_{\rm c}} \right)}^{0.272} {\left( \dfrac {\tan \theta}{2} \right)}^{0.139}\phantom{00} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{-1.050} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{-0.244} & \text{Narasimha (2009)}\\
\\
K_{\rm d0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{1.093} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-1.000} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.703} (\text{Re})^{-0.436} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.936} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.187} {\left( \dfrac {1} {\tan \theta} \right)}^{-0.1988} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-1.034} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}}{\rho_{\rm f}} \right)}^{-0.217} & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
:<math>
R_{\rm f} =
\begin{cases}
K_{\rm w0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{-0.835\phantom{00}} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{2.190\phantom{0}} {\left( \dfrac {V^2_t} {R_{\rm max}g} \right)}^{-0.259\phantom{00}} {\left( {\tan \left( \dfrac{\theta}{2}\right)}  \right)}^{-0.649} {\mu_{\rm r}}^{-0.792\phantom{0}} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{1.937} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.930} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}} {\rho_{\rm f}} \right)}^{0.462} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.765} & \text{Narasimha (2009)}\\
\\
K_{\rm w0} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{-1.06787} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{2.2062} {\left( \dfrac {V^2_t} {R_{\rm max}g} \right)}^{-0.20472} {\left( {\tan \left({\dfrac \theta 2}\right)} \right)}^{-0.829} {\mu_{\rm r}}^{-0.7118} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{2.424} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.8843} {\left( \dfrac {\rho_{\rm s} - \rho_{\rm f}} {\rho_{\rm f}} \right)}^{0.523} {\left( \cos \left(\dfrac i 2 \right) \right)}^{1.793} & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
:<math>
\alpha =
\begin{cases}
K_\alpha {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{0.191} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{0.012} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.751} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.739}} {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.467} {\left( \dfrac {\left( \rho_{\rm s} - \rho_{\rm p} \right)} {\rho_{\rm s}} \right)}^{-1.670} {\mu_{\rm r}}^{-0.112} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.018} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.233}} & \text{Narasimha (2009)}\\
\\
K_\alpha {{ {{\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{0.27\phantom{0}} {\left( \dfrac {V_{\rm t}^2} {gR_{\rm max}} \right)}^{0.016} {\left( \cos \left( \dfrac {i}{2} \right) \right)}^{0.868} {\left ( \dfrac {{\left( 1 - fv \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.72\phantom{0}}} } { {{\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.567} {\left( \dfrac {\left( \rho_{\rm s} - \rho_{\rm p} \right)} {\rho_{\rm s}} \right)}^{-1.837} {\mu_{\rm r}}^{-0.127} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.182\phantom{-}} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.2}} }} & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
:<math>
Q =
\begin{cases}
K_{\rm Q0} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{0.45} {D_{\rm c}}^{2} \sqrt \dfrac P {\rho_{\rm p}} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{1.250} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{0.060} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.330} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.047} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.090} & \text{Narasimha (2009)}\\
\\
K_{\rm Q0} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{0.45} {D_{\rm c}}^{2} \sqrt \dfrac P {\rho_{\rm p}} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{1.099} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{-0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{-0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{-0.092} & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
:<math>
P =
\begin{cases}
\rho_{\rm p} \left [ Q {{K_{\rm Q0}}^{-1} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.45} {D_{\rm c}}^{-2} {\left( \dfrac {D_{\rm o}} {D_{\rm c}} \right)}^{-1.250} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.060} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.330} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.047} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.090}} \right ]^2 & \text{Narasimha (2009)}\\
\\
\rho_{\rm p} \left [ Q {{K_{\rm Q0}}^{-1} {\left( \dfrac {D_{\rm i}} {D_{\rm c}} \right)}^{-0.45} {D_{\rm c}}^{-2} {\left( \dfrac {D_{\rm o}} {d_c} \right)}^{-1.099} {\left( \dfrac {D_{\rm u}} {D_{\rm c}} \right)}^{-0.037} {\left( {\tan \left( \dfrac \theta 2 \right)} \right)}^{0.405} {\left( \dfrac {L_{\rm c}} {D_{\rm c}} \right)}^{-0.30\phantom{0}} {\left( \dfrac {{\left( 1 - f_{\rm v} \right)}^2} {10^{1.82f_{\rm v}}} \right)}^{0.048} {\left( \cos \left( \dfrac i 2 \right) \right)}^{0.092}} \right ]^2 & \text{Narasimha et al. (2014)}\\
\end{cases}
</math>
--->

Latest revision as of 07:31, 1 August 2024

Description

This article describes the Narasimha-Mainza model for hydrocyclone size classification.

Narasimha et al. (2014a) describe an empirical hydrocyclone model that improves on the Plitt and Nageswararao approaches with the addition of several features:[1]

  • A sharpness of separation equation
  • A slurry viscosity term that includes the effects of very fine particles
  • Terms for cyclone inclination, particle density, g-forces, flow regime (Reynolds Number) and turbulent diffusion

Narasimha et al. (2014b) subsequently presented a multi-component version of the same model, with revised equations for cut size and sharpness of separation per ore component:[2]

Model theory

Figure 1. The dimensions of a hydrocyclone required by the Narasimha-Mainza model.

The Narasima-Mainza model comprises an equation for the efficiency curve (partition to overflow) and several sub-equations that describe its parameters:

  • the corrected cut size
  • the sharpness of separation
  • liquid recovery to underflow

In addition, a relationship between throughput and operating pressure is presented.

Efficiency curve

The Narasimha-Mainza model applies the Whiten-Beta efficiency curve to partition particles to the overflow stream:

where:

  • is the index of the size interval, , is the number of size intervals
  • is the fraction of particles of size interval in the feed reporting to the overflow stream (frac)
  • is the geometric mean size of particles in size interval (mm)
  • is the corrected size at which 50% of the particle mass reports to underflow and 50% to overflow (mm)
  • is the fraction of feed liquids (or fines) split to overflow (frac)
  • is a parameter representing the sharpness of separation
  • is a term introduced to accommodate the so-called fish-hook effect, and controls the initial rise in the efficiency curve at finer sizes
  • is computed to ensure the Whiten-Beta function preserves the definition of in the presence of the fish-hook, i.e. at

Corrected cut size

The corrected cut size, (m), is computed from:

where:

  • is a calibration factor which should be fitted to operating data
  • is diameter of the cyclone (m)
  • is diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet (m)
  • is diameter of the vortex finder (overflow) (m)
  • is diameter of the apex/spigot (underflow) (m)
  • is length of the cylindrical section (m)
  • is the cone full angle (deg.)
  • is the angle of inclination from the vertical (rad)
  • is the volume fraction of solids in the feed (v/v)
  • is the density of solids in the feed (t/m3)
  • is the density of the fluid (liquids) in the feed (t/m3)
  • is acceleration due to gravity (m/s2)

The Reynolds Number, , is:

The feed inlet velocity, (m/s), is:

where is the volumetric feed flow rate (m3/h), and is the density of the feed pulp (t/m3).

The relative slurry viscosity, , is the ratio of slurry and water viscosities, and , which is approximated by:

where is the cumulative fraction passing 38 μm in the feed (frac).

Liquids recovery

The fraction of feed liquid recovered to the underflow stream, , is related to (i.e. ), and is computed as:

where is a calibration factor which should be fitted to operating data.

is the radius of the cyclone (m), i.e.:

and the tangential velocity, (m/s), is:

Sharpness of separation

The sharpness of separation parameter, , is:

where is a calibration factor which should be fitted to operating data.

Cyclone capacity

The volumetric capacity of a cyclone at a given operating pressure, (m3/h), is estimated from the pressure-throughput relationship:

where is a calibration factor which should be fitted to operating data, and is the pressure drop across the operating cyclone (kPa).

This expression may be used to estimate the number of cyclones required to accept a given total cluster feed flow rate at a fixed pressure, e.g. a process set point.

Alternatively, the pressure drop arising from a given feed flow rate may be calculated by rearranging the above equation:

Multi-component modelling

Narasimha, Mainza and Holtham (2014)

The Narasimha-Mainza model formulation only considers the classification of solid particles with a single average feed density, .

Narasimha et al. (2014b) explored the classification of multi-component feeds, deriving modified equations for cut size and sharpness of separation per ore component:[2]

and

where is the density of solid ore component (t/m3).

A multi-component version of the Narasimha-Mainza model is available which replaces the average density cut size and sharpness of separation equations with their per ore equivalents above. The multi-component version is named as Narasimha-Mainza (Multi) to distinguish it from the primary Narasimha-Mainza (2014) formulation.

Silveira, Delboni and Bergerman (2024)

More recently, Silveira et al. (2024) simulated multicomponent classification with the Narasimha-Mainza model by assigning separate cut size and sharpness coefficients to the valuable mineral phase and overall ore partitions.[3]

This concept is extended here to allow the specification of cut size and sharpness coefficients for each ore/mineral/class type in the feed, i.e. and replacing and .

Partition metrics

Several metrics are provided to characterise the partition curve.

The , also known as the cut or separation size, is defined as the size of a particle which has an even (50%) chance of appearing in either the underflow or overflow stream. The size is estimated via a log-linear interpolation of geometric mean size () against the uncorrected partition to underflow of all solids in the feed.

The Ecart Probable, or , is a measure of the deviation of a partition curve from a perfect separation, and is typically defined for size classification as:[4]

where and are the sizes of particles which have a 75% and 25% probability, respectively, of appearing in the underflow stream. The and sizes are estimated by log-linear interpolation of geometric mean size against the uncorrected partition to underflow of all solids in the feed.

The Imperfection, , is a normalised measure of the sharpness of separation, which is suggested to be independent of the magnitude of the , and is typically defined for size classification as:[4]

Roping

Several methods are available to identify the potential for roping discharge from a hydrocyclone underflow.

Plitt proposed that roping may occur when when the volumetric feed rate to the cyclone, (m3/h), exceeds a solids capacity limit:[5]

Plitt further proposed a limit to the volume fraction of solids in cyclone underflow, (% v/v), of:

where is the mass median particle size of the underflow, computed here as the P50 (μm).

The SPOC criterion indicates roping may occur when:[6]

where is the percentage volume fraction of solids in the underflow stream (% v/v). The SPOC criterion is only valid when .

Investigations by Bustamante (1991) and Concha et al. (1996) led to the limiting values of cyclone geometry in Table 1:[4]

Table 1. Transition from spray to roping discharge (after Gupta and Yan, 2016).[4]
Source Condition
Bustamante <0.34 Roping discharge
0.34 - 0.5 Roping or spray
>0.5 Spray discharge
Concha et al. <0.45 Roping discharge
0.45 - 0.56 Roping or spray
>0.56 Spray discharge

Additional notes

Note that the equations presented by Narasimhsa et al. (2014) differ from those presented in Narasimha's original dissertation.[7]

The user should be aware of which model formulation is being applied when adopting calibration parameters from external sources. Recalibration of model parameters via the Excel interface below is recommended in such cases.

Excel

The Narasimha-Mainza hydrocyclone model may be invoked from the Excel formula bar with the following function call: 

=mdUnit_Hydrocyclone_NarasimhaMainza(Parameters as Range, Size as Range, Feed as Range, OreSG Range, Optional Kd0 as Range, Optional Kalpha0 as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

Inputs

The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:


where:

  • is the set of equations to use (0 = Narasimha et al. (2014), 1 = Narasimha et al. (Multi))
  • indicates whether the number of cyclones required at the given feed flow rate and pressure set point is returned (TRUE) or the operating pressure at the given feed flowrate and number of cyclones is returned (FALSE)
  • is the number of cyclones operating in a cluster. The number of cyclones is ignored if is TRUE (the value is returned in the results instead)
  • , the operating pressure, is ignored if is FALSE (the value is returned in the results instead)
  • is the density of liquids (fluids) in the feed (t/m3)
  • is the size of the square mesh interval that feed mass is retained on (mm)
  • is the number of ore types
  • is feed solids mass flow rate by size and ore type (t/h)
  • is the mass flow feed rate of liquids into the cyclone (t/h)
  • indicates optional arrays to specify cut size and sharpness parameters by ore/mineral/class type. If either array is omitted (default), the and values supplied in the array are used instead.

Results

The results are displayed in Excel as an array corresponding to the matrix notation below:


where:

  • is the number of cyclones required at the given and operating pressure , if = TRUE
  • is the volumetric feed flow rate per cyclone (m3/h)
  • is the total volumetric feed flow rate to the cluster of cyclones (m3/h)
  • is the pressure drop across the cyclone cluster with operating at feed rate , if = FALSE (kPa)
  • is actual split of liquids to the overflow (frac)
  • is the mass flow rate of liquids to the overflow stream (t/h)
  • is the mass flow rate of liquids to the underflow stream (t/h)
  • is the SPOC roping limit of volume fraction solids in the underflow stream (v/v)
  • is the Plitt roping limit of volumetric flow rate of solids in the underflow stream (m3/h)
  • is the Plit roping limit of volume fraction solids in the underflow stream (v/v)
  • is the underflow discharge type based on the Bustamante geometry limits (spray or roping discharge)
  • is the underflow discharge type based on the Concha geometry limits (spray or roping discharge)
  • is mass flow rate of solids to the underflow stream (t/h)
  • is mass flow rate of solids to the overflow stream (t/h)
  • is the actual partition of all particles of size to the overflow stream, computed as (frac)

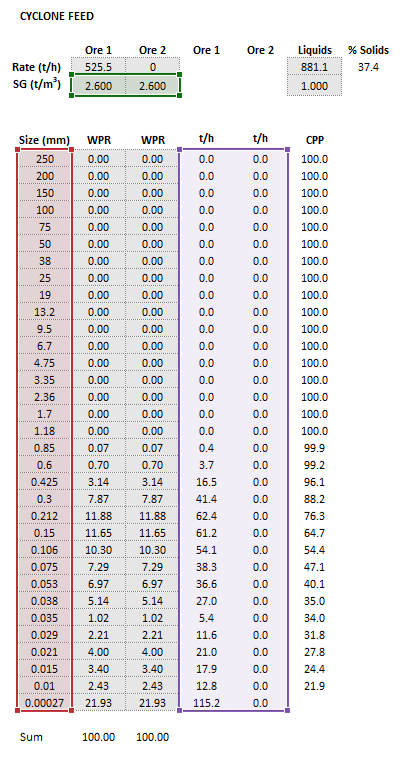
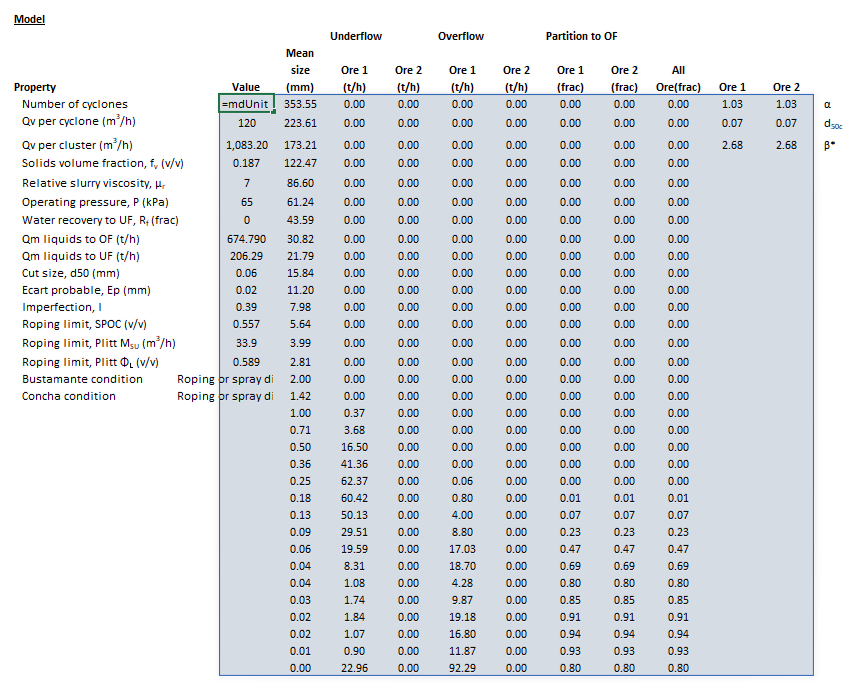
Example

The images below show the selection of input arrays and output results in the Excel interface.

Figure 2. Example showing the selection of the Parameters (blue frame) array in Excel.
Figure 3. Example showing the selection of the Size (red frame), Feed (purple frame) and OreSG (green frame) arrays in Excel.
Figure 4. Example showing the outline of the Results (light blue frame) array in Excel.

SysCAD

The sections and variable names used in the SysCAD interface are described in detail in the following tables.

MD_Hydrocyclone page

The first tab page in the access window will have this name.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Tag Display This name tag may be modified with the change tag option.
Condition Display OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount Display The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc Display This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.

If this field is blank, then SysCAD will display the unit class ID.

Requirements
On CheckBox This enables the unit. If this box is not checked, then the MassFracToUF option appears below.
MassFracToUF Input Only appears if the On field above is not checked. Specifies the fraction of feed mass that reports to the underflow stream when the model is off.
Method Partition (User) The partition to overflow for each size interval is defined by the user. Different values can be used for different solids.
Partition (Reid-Plitt) The partition to overflow for each size interval is defined by a Reid-Plitt efficiency curve. Different parameters can be used for different solids.
Partition (Whiten-Beta) The partition to overflow for each size interval is defined by a Whiten-Beta efficiency curve. Different parameters can be used for different solids.
Nageswararao The Nageswararao model is used to determine the partition of solids to underflow and overflow for each size interval.
Narasimha-Mainza (2014) The Narasimha-Mainza (2014) model is used to determine the partition of solids to underflow and overflow for each size interval.
Narasimha-Mainza (Multi) The Narasimha-Mainza (Multi) model is used to determine the partition of solids to underflow and overflow for each size interval.
Plitt The Plitt model is used to determine the partition of solids to underflow and overflow for each size interval.
RopingCalcs CheckBox Show addition calculations that predict the onset of cyclone underflow roping.
Options
ShowQFeed CheckBox QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream.
ShowQOF CheckBox QOF and associated tab pages (eg Sp) will become visible, showing the properties of the overflow stream.
ShowQUF CheckBox QUF and associated tab pages (eg Sp) will become visible, showing the properties of the underflow stream.
SizeForPassingFracCalc Input Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section.
FracForPassingSizeCalc Input Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section.
Stream Summary
MassFlow / Qm Display The total mass flow in each stream.
SolidMassFlow / SQm Display The Solids mass flow in each stream.
LiquidMassFlow / LQm Display The Liquid mass flow in each stream.
VolFlow / Qv Display The total Volume flow in each stream.
Temperature / T Display The Temperature of each stream.
Density / Rho Display The Density of each stream.
SolidFrac / Sf Display The Solid Fraction in each stream.
LiquidFrac / Lf Display The Liquid Fraction in each stream.
Passing Display The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream.
Passes Display The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction.

Cyclone page

The Cyclone page is used to specify the input parameters for the hydrocyclone model.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
NarasimhaMainza
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
PressureControl CheckBox If enabled, the number of cyclones is adjusted to maintain operating pressure at the feed volumetric flow rate.
OreSpecific CheckBox Only appears if the Narasimha-Mazina (2014) model method is selected. If enabled, allows Kd0 and Kalpha parameters to be specified per species.
Dimensions
NumberCyclones / NumCyclones Input The number of operating cyclone units in the cluster.
CycloneDiameter / Dc Input Diameter of the cyclone.
InletDiameter / Di Input Diameter of a circular inlet or the diameter of a circle with the same area as a non-circular inlet.
CycloneDiameter / Dc Input Diameter of the cyclone.
OverflowDiameter / Do Input Diameter of the vortex finder (overflow).
UnderflowDiameter / Du Input Diameter of the apex/spigot (underflow).
CylSectLength / Lc Input Length of the cylindrical section of the cyclone.
ConeFullAngle / Theta Input Full angle of the cone section of the cyclone.
InclinationAngle/ i Input Angle of inclination of cyclone from the vertical.
Parameters
Kd0 Input Calibration factor for the d50c equation.
KQ0 Input Calibration factor for the pressure-flowrate equation
Kw0 Input Calibration factor for the liquids recovery to underflow equation.
Kalpha0 Input Calibration factor for the sharpness of separation eqaution.
Beta Input 'Fish hook' parameter of the Whiten-Beta efficiency curve equation.
Liquids
LiquidsSeparMethod Split To UF (User) Liquids are split to underflow by a user-defined fraction of liquids in the feed.
Split To UF (Model) Liquids are split to underflow by a fraction computed by the associated model.
UF Solids Fraction Sufficient liquids mass is recovered to the underflow stream to yield the user-defined underflow solids mass fraction value (if possible).
UF Liquids Fraction Sufficient liquids mass is recovered to the underflow stream to yield the user-defined underflow liquids mass fraction value (if possible).
UFSolidsFracReqd / UF.SfReqd Input Required value of the mass fraction of solids in the underflow stream. Only visible if UF Solids Fraction is selected.
UFLiquidsFracReqd / UF.LfReqd Input Required value of the mass fraction of liquids in the underflow stream. Only visible if UF Liquids Fraction is selected.
LiqSplitToUF / UF.LiqSplit Input/Display The fraction of liquids recovered to underflow.
Results
ClusterQv / Cluster.Qv Display Volumetric flow rate of feed to the cyclone cluster (i.e. total flow).
CycloneQv / Cyclone.Qv Display Volumetric flow rate of feed to each cyclone in the cluster (i.e. per cyclone flow).
OperatingPressure / P Display Pressure drop across the cyclone.
VolFracSolids / fv Display Volume fraction of solids in feed stream.
RelSlurryVisc / mur Display Relative slurry viscosity.
Rf Display Fraction of feed liquids recovered to underflow stream.
d50 Display The separation size, d50, of all solid particles in the feed.
EcartProbable / Ep Display The value of the Ecart Probable of the separation.
Imperfection / I Display The value of the Imperfection of the separation.
Alpha Display Value of , per species.
d50c Display Value of the corrected d50c, per species.
Beta* Display Value of , per species.

Partition page

The Partition page is used to specify or display the partition by species and size values.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Distribution
Name Display Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream.
IntervalCount Display Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream.
SpWithPSDCount Display Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality.
Partition
Method Model/User Select model-calculated or user-defined partition to separate each solids species type.
Density Display Density of each solid species.
Size Display Size of each interval in mesh series.
MeanSize Display Geometric mean size of each interval in mesh series.
All (All column) Display
  • Actual overall partition to overflow of all solid species, for each size interval.
  • Excludes solid species not present in the cyclone feed.
Partition Display
  • Partition to overflow for each size interval, in each solid species, as determined by the selected model or user defined value.
  • Note: These values are displayed regardless of whether the solid species is present in the cyclone feed or not.
All (All row, All column) Display
  • Displays the actual, total, partition of all solids with a particle size distribution property in the feed to overflow.
  • Excludes solid species not present in the cyclone feed.
All (All row, per species) Display
  • Actual overall partition to overflow for each solid species, for all size intervals in that species.
  • Excludes solid species not present in the cyclone feed.

Roping page

This page displays the results for hydrocyclone roping limit calculations. The page is only visible if Roping is selected on the MD_Hydrocyclone page.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Roping
Underflow
SolidsVolFlow / SQv Display Volumetric flow rate of solids in cyclone underflow stream.
Plitt.MSu Display Plitt's volumetric flow rate of solids in cyclone underflow roping limit.
SolidsVolFrac / Svf Display Volume fraction of solids in the cyclone underflow stream.
SPOC Display SPOC volume fraction of solids in the cyclone underflow roping limit.
Plitt.phiL Display Plitt's volume fraction of solids in the cyclone underflow roping limit.
Geometry
BCondition Display Text string describing the spray/roping condition of the cyclone based on Bustamante's geometry limits.
CCondition Display Text string describing the spray/roping condition of the cyclone based on the Concha et al. geometry limits.

About page

This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
About
HelpLink ButtonLicensingHelp.png Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required.
Information ButtonCopyToClipboard.png Copies Product and License information to the Windows clipboard.
Product
Name Display Met Dynamics software product name
Version Display Met Dynamics software product version number.
BuildDate Display Build date and time of the Met Dynamics Models SysCAD Add-On.
License
File ButtonBrowse.png This is used to locate a Met Dynamics software license file.
Location Display Type of Met Dynamics software license or file name and path of license file.
SiteCode Display Unique machine identifier for license authorisation.
ReqdAuth Display Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime.
Status Display License status, LICENSE_OK indicates a valid license, other messages report licensing errors.
IssuedTo Display Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to.
ExpiryDate Display Only visible if Met Dynamics license file is used. License expiry date.
DaysLeft Display Only visible if Met Dynamics license file is used. Days left before the license expires.

Additional notes

  • Solid species that do not possess a particle size distribution property are split according to the overall mass split of the default particle size distribution species selected in the SysCAD Project Configuration.
  • If the default particle size distribution species is not present in the unit feed, the overall split of all other species with particle size distributions combined is used, as determined by the model.
  • Gas phase species report directly to the overflow stream without split.

See also

References

  1. ↑ Narasimha, M., Mainza, A.N., Holtham, P.N., Powell, M.S. and Brennan, M.S., 2014. A semi-mechanistic model of hydrocyclones—Developed from industrial data and inputs from CFD. International Journal of Mineral Processing, 133, pp.1-12.
  2. ↑ 2.0 2.1 Narasimha, M., Crasta, J, Sreenivas, T. and Mainza, A. N., 2014. Performance of hydrocyclone separating bi-component mixture. In Proceedings of the XXVII International Mineral Processing Congress, Santiago, Chile, 2014.
  3. ↑ Silveira Jr, A., Delboni Jr, H. and Bergerman, M.G., 2024. Modeling and Simulation of Hydroxyapatite Recovery in the Desliming Circuit of the Tapira Industrial Plant, Brazil. Minerals, 14(3), p.272.
  4. ↑ 4.0 4.1 4.2 4.3 Gupta, A. and Yan, D.S., 2016. Mineral processing design and operations: an introduction. Elsevier.
  5. ↑ Dubey, R.K., Singh, G. and Majumder, A.K., 2017. Roping: Is it an optimum dewatering performance condition in a hydrocyclone?. Powder Technology, 321, pp.218-231.
  6. ↑ Napier-Munn, T.J., Morrell, S., Morrison, R.D. and Kojovic, T., 1996. Mineral comminution circuits: their operation and optimisation. Julius Kruttschnitt Mineral Research Centre, Indooroopilly, QLD.
  7. ↑ Narasimha, M., 2009. Improved Computational and Empirical Models of Hydrocyclones. PhD Thesis, University of Queensland (unpublished).
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Hydrocyclone_(Narasimha-Mainza)&oldid=2090"