Tumbling Mill (Media Trajectory): Difference between revisions
Scott Munro (talk | contribs) m (1 revision imported) |
imported>Scott.Munro m (→Model theory) |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 14: | Line 14: | ||
== Model theory == | == Model theory == | ||
{{Restricted content}} | |||
[[File: | <hide> | ||
[[File:TumblingMillMediaTraj2.png|thumb|625px|Figure 2. Geometric diagram of an outer media element resting on a lifter bar in a tumbling mill at the point of equilibrium (after Powell, 1991).{{Powell (1991)}}]] | |||
[[File: | [[File:TumblingMillMediaTraj3.png|thumb|525px|Figure 3. Geometric diagram of a lifter bar (after Powell, 1991).{{Powell (1991)}}]] | ||
Powell | [[File:TumblingMillMediaTraj4.png|thumb|475px|Figure 4. Geometric diagram of an outer media element resting on a lifter bar lower than the element radius in a tumbling mill at the point of equilibrium (after Powell, 1991).{{Powell (1991)}}]] | ||
Powell's theory derives equations of motion for the outer media elements in a rotating tumbling mill based on a consideration of the acting gravitational, centrifugal and frictional forces.{{Powell (1991)}} | |||
Outer elements are those that are initially in contact with both a lifter bar and the mill shell. The equations of motion are valid for both rod- or ball-type media elements, with minor formulation differences as outlined below. | Outer elements are those that are initially in contact with both a lifter bar and the mill shell. The equations of motion are valid for both rod- or ball-type media elements, with minor formulation differences as outlined below. | ||
| Line 32: | Line 35: | ||
The equations of motion for each state are summarised below, with reference to the diagrams in Figures 2 and 3. Derivation of the equations is excluded from the summary. | The equations of motion for each state are summarised below, with reference to the diagrams in Figures 2 and 3. Derivation of the equations is excluded from the summary. | ||
</hide><div class="user-show"> | |||
=== Point of equilibrium === | === Point of equilibrium === | ||
</div><hide> | |||
At the point of equilibrium, the sum of downward gravitational force, outward radial centrifugal force, normal force of the lifter bar, and frictional force between the lifter surface and the media element is zero. | At the point of equilibrium, the sum of downward gravitational force, outward radial centrifugal force, normal force of the lifter bar, and frictional force between the lifter surface and the media element is zero. | ||
| Line 48: | Line 53: | ||
where: | where: | ||
* <math>\kappa</math> is the friction angle, related to the coefficient of static friction between the lifter bar and the media element, <math>\ | * <math>\kappa</math> is the friction angle, related to the coefficient of static friction between the lifter bar and the media element, <math>\mu_{\rm s}</math>, by <math>\mu_{\rm s} = \tan \kappa</math>. If the effects of static friction are ignored, <math>\mu_{\rm s} = 0 \implies \kappa = 0</math>. | ||
* <math>\Omega</math> is the angular velocity of the mill (rad/s) | * <math>\Omega</math> is the angular velocity of the mill (rad/s) | ||
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>) | * <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>) | ||
| Line 63: | Line 68: | ||
where the distance <math>\delta</math> (m) is: | where the distance <math>\delta</math> (m) is: | ||
:<math>\delta = (R - | :<math>\delta = (R - h_{\rm r}) \cdot \sin \alpha - a</math> | ||
and <math> | and <math>h_{\rm r}</math> is the radial height of the lifter bar (m) and <math>\alpha</math> is the angle between the lifter bar face and a radial line from the centre of the mill through the tip of the lifter bar (rad). | ||
The angle <math>\alpha</math> is related to the lifter bar geometry by the following equations:{{Powell (1988)}} | The angle <math>\alpha</math> is related to the lifter bar geometry by the following equations:{{Powell (1988)}} | ||
| Line 84: | Line 89: | ||
* <math>y</math> is half the width of the lifter bar (m). | * <math>y</math> is half the width of the lifter bar (m). | ||
The radial height of the lifter bar, <math> | The radial height of the lifter bar, <math>h_{\rm r}</math>, is the length of the radial line between the tip of the lifter and the base, and is defined as: | ||
:<math> | :<math>h_{\rm r} = R - \frac{\sqrt{R^2 - y^2} - h}{\cos \psi}</math> | ||
The angle <math>\lambda</math> will always be <math>\frac{\pi}{2}</math> (i.e. 90°) when the lifter bar surface is tangent to the media element, i.e. when the lifter height exceeds the media element radius, as illustrated in Figure 2. However, if the lifter height is lower than the media element radius, <math>\lambda</math> is greater than 90°, as illustrated in Figure 4, and is computed as: | The angle <math>\lambda</math> will always be <math>\frac{\pi}{2}</math> (i.e. 90°) when the lifter bar surface is tangent to the media element, i.e. when the lifter height exceeds the media element radius, as illustrated in Figure 2. However, if the lifter height is lower than the media element radius, <math>\lambda</math> is greater than 90°, as illustrated in Figure 4, and is computed as: | ||
:<math>\lambda = \pi - \arccos \left ( \dfrac{a^2 + (R - | :<math>\lambda = \pi - \arccos \left ( \dfrac{a^2 + (R - h_{\rm r})^2 - r_0^2}{2 a (R - h_{\rm r})} \right ) - \alpha</math> | ||
A different formulation of <math>\gamma_0</math> at the point of equilibrium arises from the force balance when <math>\lambda</math> is greater than 90°. | A different formulation of <math>\gamma_0</math> at the point of equilibrium arises from the force balance when <math>\lambda</math> is greater than 90°. | ||
| Line 102: | Line 107: | ||
:<math>(r_0,\phi_0) =\left ( r_0, \gamma_0 - \beta_0 \right )</math> | :<math>(r_0,\phi_0) =\left ( r_0, \gamma_0 - \beta_0 \right )</math> | ||
</hide><div class="user-show"> | |||
=== Lifter bar tip position === | === Lifter bar tip position === | ||
</div><hide> | |||
The position of a media element at tip of the lifter bar is defined by the following parameters: | The position of a media element at tip of the lifter bar is defined by the following parameters: | ||
:<math> | :<math>s_{\rm L} = (R - h_{\rm r}) \cdot \cos \alpha</math> | ||
:<math>\ | :<math>\beta_{\rm L} = \arctan \left ( \frac{\delta}{s_{\rm L}} \right )</math> | ||
where <math> | where <math>s_{\rm L}</math> is the position of the media element along the lifter face surface at the tip of the lifter (m), and <math>\beta_{\rm L}</math> (rad) is the angle between the radial line passing through the centre of the media element at the tip of the lifter and the lifter bar face (rad). | ||
In between the point of equilibrium and the lifter bar tip, a media element may roll, slide or be projected into free flight depending on the prevailing forces. | In between the point of equilibrium and the lifter bar tip, a media element may roll, slide or be projected into free flight depending on the prevailing forces. | ||
</hide><div class="user-show"> | |||
=== Rolling === | === Rolling === | ||
</div><hide> | |||
If the coefficient of static friction between the lifter and the media element, <math>\ | If the coefficient of static friction between the lifter and the media element, <math>\mu_{\rm s}</math>, is greater than zero then the element commences movement from the point of equilibrium by pure rolling down the lifter face. | ||
However, if the effects of static friction are ignored, rolling does not occur and the element only experiences sliding motion (see [[Tumbling Mill (Media Trajectory)#Sliding|Sliding]] below). | However, if the effects of static friction are ignored, rolling does not occur and the element only experiences sliding motion (see [[Tumbling Mill (Media Trajectory)#Sliding|Sliding]] below). | ||
==== Pure rolling ==== | </hide><div class="user-show"> | ||
==== Pure rolling ==== | |||
</div><hide> | |||
The moments of inertia of ball (spherical) and rod (cylindrical) media elements are different, which leads to separate formulations of the equations of motion whilst rolling. | The moments of inertia of ball (spherical) and rod (cylindrical) media elements are different, which leads to separate formulations of the equations of motion whilst rolling. | ||
| Line 152: | Line 163: | ||
</math> | </math> | ||
The time at which a media element undergoing pure rolling will reach the tip of the lifter, <math> | The time at which a media element undergoing pure rolling will reach the tip of the lifter, <math>t_{\rm L}</math> (s), may be found by setting <math>s(t) = s_{\rm L}</math> and solving for <math>t</math>. This will require a numerical solution, as <math>t</math> cannot be algebraically isolated in the equation for <math>s(t)</math> above. | ||
The velocity of the media element may be found by substituting the value of <math> | The velocity of the media element may be found by substituting the value of <math>t_{\rm L}</math> obtained into the equation for <math>\dot s</math> under pure rolling. The angle of the lifter bar face when the media element is at the tip of the lifter is similarly <math>\gamma_{\rm L} = \gamma_0 + \Omega t_{\rm L}</math> under pure rolling. | ||
</hide><div class="user-show"> | |||
==== Maximum angle for pure rolling ==== | ==== Maximum angle for pure rolling ==== | ||
</div><hide> | |||
During pure rolling and prior to reaching the lifter tip, the frictional force causing angular acceleration of the element may be exceeded by the acting gravitational and centrifugal forces. At this point, the element begins to slip across the lifter face, in addition to continued rolling. | During pure rolling and prior to reaching the lifter tip, the frictional force causing angular acceleration of the element may be exceeded by the acting gravitational and centrifugal forces. At this point, the element begins to slip across the lifter face, in addition to continued rolling. | ||
A potential transition from pure rolling to combined rolling and sliding between the point of equilibrium and the tip of the lifter bar can be detected by finding the minimum possible value of the maximum angle for pure rolling, <math>\gamma_{m | A potential transition from pure rolling to combined rolling and sliding between the point of equilibrium and the tip of the lifter bar can be detected by finding the minimum possible value of the maximum angle for pure rolling, <math>\gamma_{\rm m(min)}</math> (rad), i.e. where the following inequality no longer holds: | ||
:<math>\sin \gamma_{m | :<math>\sin \gamma_{\rm m(min)} - c_4 \mu_{\rm s} \cdot \cos \gamma_{\rm m(min)} \leq \dfrac{\Omega^2}{g} \left ( c_4 \delta \mu_{\rm s} + s_{\rm L} \right)</math> | ||
where: | where: | ||
| Line 174: | Line 187: | ||
</math> | </math> | ||
The variable <math>\gamma_{m | The variable <math>\gamma_{\rm m(min)}</math> must be solved by numerical approximation. | ||
If the angle of the lifter bar face when the media element is at the tip of the lifter after pure rolling , <math>\ | If the angle of the lifter bar face when the media element is at the tip of the lifter after pure rolling , <math>\gamma_{\rm L}</math>, exceeds <math>\gamma_{\rm m(min)}</math> then a transition to combined rolling and sliding is possible. Otherwise, the media element only undergoes pure rolling before being projected into free flight. | ||
</hide><div class="user-show"> | |||
==== Transition to rolling and sliding ==== | ==== Transition to rolling and sliding ==== | ||
</div><hide> | |||
The time at which a transition from pure rolling to combined rolling and sliding occurs, <math> | The time at which a transition from pure rolling to combined rolling and sliding occurs, <math>t_{\rm I}</math> (s), is found by numerically solving for <math>t</math> where the following inequality no longer holds: | ||
:<math>c_5 . \sin (\gamma_0 + \Omega t ) - c_4 \ | :<math>c_5 . \sin (\gamma_0 + \Omega t ) - c_4 \mu_{\rm s} \cdot \cos (\gamma_0 + \Omega t ) \leq | ||
c_4.\dfrac{\Omega^2}{g} \delta \ | c_4.\dfrac{\Omega^2}{g} \delta \mu_{\rm s} + \left ( \dfrac{s_0}{g}\Omega^2 - c_1 \sin \gamma_0 \right ) \cdot \cosh \left ( c_2 . \Omega t \right ) - c_6 \sqrt{3} \cos \gamma_0 \cdot \sinh \left ( c_2 . \Omega t \right )</math> | ||
where: | where: | ||
| Line 201: | Line 216: | ||
</math> | </math> | ||
The position, <math> | The position, <math>s_{\rm I}</math> (m), and velocity, <math>\dot s_{\rm I}</math> (m), of the media element at <math>t_{\rm I}</math> can then be computed using the pure rolling equations for <math>s(t)</math> and <math>\dot s</math> above. The angle of the lifter bar face at <math>t_{\rm I}</math>, <math>\gamma_{\rm I}</math> (rad), is found from <math>\gamma_{\rm I} = \gamma_0 + \Omega t_{\rm I}</math>. | ||
</hide><div class="user-show"> | |||
=== Sliding === | === Sliding === | ||
</div><hide> | |||
</hide><div class="user-show"> | |||
==== Sliding after rolling ==== | ==== Sliding after rolling ==== | ||
</div><hide> | |||
If sliding motion commences after rolling, the position and velocity of the element at time <math>\tau</math> are: | If sliding motion commences after rolling, the position and velocity of the element at time <math>\tau</math> are: | ||
:<math>s(\tau) = \left( | :<math>s(\tau) = \left( s_{\rm I} + \mu_{\rm k} \delta + \dfrac{g}{2 \Omega^2} (\mu_{\rm k} \cos \gamma_{\rm I} - \sin \gamma_{\rm I}) \right ) \cosh (\Omega \tau) + \left ( \dfrac{\dot s_{\rm I}}{\Omega} - \dfrac{g}{2 \Omega^2} (\mu_{\rm k} \sin \gamma_{\rm I} + \cos \gamma_{\rm I} ) \right ) \sinh (\Omega \tau) - \dfrac{g}{2 \Omega^2} \big( \mu_{\rm k} \cos (\gamma_{\rm I} + \Omega \tau) - \sin (\gamma_{\rm I} + \Omega \tau) \big) - \mu_{\rm k} \delta</math> | ||
:<math>\dot s = \Omega \left ( | :<math>\dot s = \Omega \left ( s_{\rm I} + \mu_{\rm k} \delta + \dfrac{g}{2 \Omega^2} (\mu_{\rm k} \cos \gamma_{\rm I} - \sin \gamma_{\rm I} \right ) \sinh (\Omega \tau) + \left ( \dot s_{\rm I} -\dfrac{g}{2 \Omega} (\mu_K \sin \gamma_{\rm I} + \cos \gamma_{\rm I} \right ) \cosh (\Omega \tau) - \dfrac{g}{2 \Omega} \big( -\mu_{\rm k} \sin (\gamma_{\rm I} + \Omega \tau) - \cos (\gamma_{\rm I} + \Omega \tau) \big )</math> | ||
where <math>\ | where <math>\mu_{\rm k}</math> is the coefficient of kinematic friction between the lifter bar face and the media element. | ||
The time at which the media element reaches the tip of the lifter, <math>\ | The time at which the media element reaches the tip of the lifter, <math>\tau_{\rm L}</math> (s), after the transition to sliding is found by setting <math>s(\tau)=s_{\rm L}</math> and numerically solving for <math>\tau</math>. The velocity <math>\dot s_{\rm L}</math> (m/s) and angular position <math>\gamma_{\rm L}</math> (rad) of the media element at the tip of the lifter after sliding then follow from the value of <math>\tau_{\rm L}</math> obtained (i.e., <math>\gamma_{\rm L} = \gamma_{\rm I} + \Omega \tau</math>). | ||
The total time for the media element to travel from the point of equilibrium to the tip of the lifter bar by rolling and sliding is <math> | The total time for the media element to travel from the point of equilibrium to the tip of the lifter bar by rolling and sliding is <math>t_{\rm L} = t_{\rm I} + \tau_{\rm L}</math> (s). | ||
</hide><div class="user-show"> | |||
==== Pure sliding ==== | ==== Pure sliding ==== | ||
</div><hide> | |||
If the coefficient of static friction (<math>\ | If the coefficient of static friction (<math>\mu_{\rm s}</math>) is zero, i.e. ignored, rolling does not commence and the media element undergoes sliding directly from the point of equilibrium. The above equations of motion for sliding are subsequently utilised with the following values substituted: | ||
:<math> | :<math>s_{\rm I} = s_0, \;\;\;\;\; | ||
\dot | \dot s_{\rm I} = 0, \;\;\;\;\; | ||
\ | \gamma_{\rm I} = \gamma_0</math> | ||
and <math> | and <math>t_{\rm L} = \tau_{\rm L}</math>. | ||
</hide><div class="user-show"> | |||
=== Free-flight === | === Free-flight === | ||
</div><hide> | |||
A media element may be projected into free flight in two ways: | A media element may be projected into free flight in two ways: | ||
| Line 245: | Line 268: | ||
The polar coordinates of the media element position at the point it leaves the lifter are (m, rad): | The polar coordinates of the media element position at the point it leaves the lifter are (m, rad): | ||
:<math>( | :<math>(r_{\rm L},\, \phi_{\rm L}) =\left ( \dfrac{s_{\rm L}}{\cos \beta_{\rm L}},\; \gamma_{\rm L} - \beta_{\rm L} \right )</math> | ||
Switching to a Cartesian coordinate frame of reference yields the following position <math>( | Switching to a Cartesian coordinate frame of reference yields the following position <math>(x_{\rm L},y_{\rm L})</math> (m) and velocity <math>(v_{x{\rm L}},v_{y{\rm L}})</math> (m/s) coordinates at the tip of the lifter bar: | ||
:<math>( | :<math>(x_{\rm L},\, y_{\rm L}) = \left ( r_{\rm L} \cos \phi_{\rm L},\; r_{\rm L} \sin \phi_{\rm L} \right )</math> | ||
:<math>(v_{ | :<math>(v_{x{\rm L}},\, v_{y{\rm L}}) = \left ( \dot s_{\rm L} \cos \gamma_{\rm L} - \Omega r_{\rm L} \sin \phi_{\rm L},\; \dot s _L \sin \gamma_{\rm L} + \Omega r_{\rm L} \cos \phi_{\rm L} \right )</math> | ||
The polar coordinates of the media element velocity as it leaves the lifter are (m/s, rad): | The polar coordinates of the media element velocity as it leaves the lifter are (m/s, rad): | ||
:<math>( | :<math>(v_{\rm L},\, \phi_{v{\rm L}}) =\left (\sqrt{{{v_{x{\rm L}}^2}} + v^2_{y{\rm L}}},\; \arctan \dfrac{v_{x{\rm L}}}{v_{y{\rm L}}} \right )</math> | ||
Once in free flight, the media element moves in a parabolic path under the influence of gravity, with a position defined as (m): | Once in free flight, the media element moves in a parabolic path under the influence of gravity, with a position defined as (m): | ||
:<math>(x,\, y) = \left ( | :<math>(x,\, y) = \left ( x_{\rm L} + v_{x{\rm L}} t,\; y_{\rm L} + v_{y{\rm L}} t - \frac{1}{2} g t^2 \right )</math> | ||
The media element impacts the mill shell when: | The media element impacts the mill shell when: | ||
| Line 265: | Line 288: | ||
:<math>x^2 + y^2 = r_0</math> | :<math>x^2 + y^2 = r_0</math> | ||
the solution of which is denoted <math>( | the solution of which is denoted <math>(x_{\rm E}, y_{\rm E})</math> (m). | ||
Finally, the polar coordinates of the media element velocity as it leaves the lifter are (m/s, rad): | Finally, the polar coordinates of the media element velocity as it leaves the lifter are (m/s, rad): | ||
:<math>( | :<math>(v_{\rm E},\, \phi_{v{\rm E}}) =\left (\sqrt{v^2_{x{\rm E}} + v^2_{y{\rm E}}},\; \arctan \dfrac{v_{x{\rm E}}}{v_{y{\rm E}}} \right )</math> | ||
where: | where: | ||
:<math>(v_{ | :<math>(v_{x{\rm E}},\, v_{y{\rm E}}) = (v_{x{\rm L}}, \; v_{y{\rm L}} - gt)</math> | ||
== Additional notes == | </hide><div class="user-show"> | ||
=== Additional notes === | |||
</div><hide> | |||
{| style="float:right; margin-left: 20px;" | {| style="float:right; margin-left: 20px;" | ||
| [[File:TumblingMillMediaTraj5.png|thumb|475px|Figure 5. Example of the measurement of the dimensions of a new lifter (pale grey line) by overlaying a scan with an Excel chart (coloured lines).]] | | [[File:TumblingMillMediaTraj5.png|thumb|475px|Figure 5. Example of the measurement of the dimensions of a '''new''' lifter (pale grey line) by overlaying a scan with an Excel chart (coloured lines).]] | ||
| [[File:TumblingMillMediaTraj6.png|thumb|475px|Figure 6. Example of the measurement of the dimensions of a worn lifter (dark grey line) by overlaying a scan with an Excel chart (coloured lines).]] | | [[File:TumblingMillMediaTraj6.png|thumb|475px|Figure 6. Example of the measurement of the dimensions of a '''worn''' lifter (dark grey line) by overlaying a scan with an Excel chart (coloured lines).]] | ||
|} | |} | ||
=== Friction estimates === | </hide><div class="user-show"> | ||
==== Friction estimates ==== | |||
</div><hide> | |||
Powell's (1991) experimental work separately investigated the coefficients of static and kinetic friction between a media element and a lifter bar. The findings suggest: | Powell's (1991) experimental work separately investigated the coefficients of static and kinetic friction between a media element and a lifter bar. The findings suggest: | ||
* Static friction (<math>\ | * Static friction (<math>\mu_{\rm s}</math>) is likely approaching zero for practical applications, and | ||
* Kinematic friction (<math>\ | * Kinematic friction (<math>\mu_{\rm k}</math>) is likely in the range of 0.17 - 0.19. | ||
Rolling motion does not occur when static friction is zero, greatly simplifying the trajectory calculations presented above. | Rolling motion does not occur when static friction is zero, greatly simplifying the trajectory calculations presented above. | ||
Adequate estimates of the coefficients of friction for simulation purposes may be 0 or 0.05 for <math>\ | Adequate estimates of the coefficients of friction for simulation purposes may be 0 or 0.05 for <math>\mu_{\rm s}</math> and 0.19 for <math>\mu_{\rm k}</math>, but is left to user discretion. | ||
=== Extracting lifter geometry === | </hide><div class="user-show"> | ||
==== Extracting lifter geometry ==== | |||
</div><hide> | |||
Modern mill interior laser scanning devices and/or design drawings provide accurate parametric maps of lifter bar geometry, which may be used to quantify the lifter height (<math>h</math>), lifter width (<math>2y</math>) and lifter face angle (<math>\rho</math>) properties for media trajectory simulation. | Modern mill interior laser scanning devices and/or design drawings provide accurate parametric maps of lifter bar geometry, which may be used to quantify the lifter height (<math>h</math>), lifter width (<math>2y</math>) and lifter face angle (<math>\rho</math>) properties for media trajectory simulation. | ||
| Line 308: | Line 337: | ||
<br> | <br> | ||
<br> | <br> | ||
</hide> | |||
== Excel == | == Excel == | ||
| Line 327: | Line 357: | ||
\text{Media type}\\ | \text{Media type}\\ | ||
d\text{ (m)}\\ | d\text{ (m)}\\ | ||
\ | \mu_{\rm s}\\ | ||
\ | \mu_{\rm k}\\ | ||
\rho\text{ (rad)}\\ | \rho\text{ (rad)}\\ | ||
h\text{ (m)}\\ | h\text{ (m)}\\ | ||
y\text{ (m)}\\ | y\text{ (m)}\\ | ||
C_{\rm s} (frac) | |||
\end{bmatrix},\;\;\;\;\;\; | \end{bmatrix},\;\;\;\;\;\; | ||
| Line 344: | Line 374: | ||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\begin{bmatrix} | \begin{bmatrix} | ||
\ | \phi_{\rm L}\text{ (rad)} & -\\ | ||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\begin{bmatrix} | \begin{bmatrix} | ||
x_{\rm L} \text{ (m)} & y_{\rm L} \text{ (m)}\\ | |||
v_{\rm L} \text{ (m)} & \phi_{v{\rm L}} \text{ (rad)}\\ | |||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\begin{bmatrix} | \begin{bmatrix} | ||
\ | \phi_{\rm E}\text{ (rad)} & -\\ | ||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\begin{bmatrix} | \begin{bmatrix} | ||
x_{\rm E} \text{ (m)} & y_{\rm E} \text{ (m)}\\ | |||
v_{\rm E} \text{ (m)} & \phi_{v{\rm E}} \text{ (rad)}\\ | |||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Line 370: | Line 400: | ||
* <math>d</math> is the media element diameter (m), i.e. <math>d = 2a</math> | * <math>d</math> is the media element diameter (m), i.e. <math>d = 2a</math> | ||
* <math>\text{Media type}</math> is the type of media element, balls or rods (''0 = Balls, 1 = Rods'') | * <math>\text{Media type}</math> is the type of media element, balls or rods (''0 = Balls, 1 = Rods'') | ||
* <math> | * <math>C_{\rm s}</math> is the fraction critical speed of the mill (frac) | ||
and: | and: | ||
| Line 383: | Line 413: | ||
The media trajectory model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown. | The media trajectory model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown. | ||
{{ | {{SysCAD (Text, Table Header)}} | ||
|- | |||
! colspan="3" style="text-align:left;" |''MediaTraj'' | |||
{{SysCAD (Text, Help Link)}} | |||
|- | |- | ||
! colspan="3" style="text-align:left;" |''Requirements'' | ! colspan="3" style="text-align:left;" |''Requirements'' | ||
| Line 425: | Line 461: | ||
! colspan="3" style="text-align:left;" |''Results'' | ! colspan="3" style="text-align:left;" |''Results'' | ||
|- | |- | ||
| colspan="3" |'' | | colspan="3" |''PointOfEquilibrium'' | ||
|- | |- | ||
| PositionAngle | | PositionAngle / Phi | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
| Angular position of the point of equilibrium. | | Angular position of the point of equilibrium. | ||
|- | |- | ||
| colspan="3" |'' | | colspan="3" |''LeavesLifter'' | ||
|- | |- | ||
|PositionAngle | |PositionAngle / Phi | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
| Angular position of the point where the media element leaves the lifter. | | Angular position of the point where the media element leaves the lifter. | ||
| Line 445: | Line 481: | ||
| Cartesian ''y'' coordinate of the point where the media element leaves the lifter. | | Cartesian ''y'' coordinate of the point where the media element leaves the lifter. | ||
|- | |- | ||
|Velocity | |Velocity / V | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
| Velocity of the media element at the point where it leaves the lifter. | | Velocity of the media element at the point where it leaves the lifter. | ||
|- | |- | ||
|VelocityAngle | |VelocityAngle / PhiV | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
| Angular direction of the velocity of the media element at the point where it leaves the lifter. | | Angular direction of the velocity of the media element at the point where it leaves the lifter. | ||
|- | |- | ||
| colspan="3" |'' | | colspan="3" |''ImpactsShell'' | ||
|- | |- | ||
|PositionAngle | |PositionAngle / Phi | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
| Angular position of the point where the media element impacts the mill shell. | | Angular position of the point where the media element impacts the mill shell. | ||
| Line 467: | Line 503: | ||
| Cartesian ''y'' coordinate of the point where the media element impacts the mill shell. | | Cartesian ''y'' coordinate of the point where the media element impacts the mill shell. | ||
|- | |- | ||
|Velocity | |Velocity / V | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
| Velocity of the media element at the point where it impacts the mill shell. | | Velocity of the media element at the point where it impacts the mill shell. | ||
|- | |- | ||
|VelocityAngle | |VelocityAngle / PhiV | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
| Angular direction of the velocity of the media element at the point where it impacts the mill shell. | | Angular direction of the velocity of the media element at the point where it impacts the mill shell. | ||
|- | |- | ||
| style="vertical-align:top;" |State | | style="vertical-align:top;" |State | ||
| | |style="vertical-align:top; background:#eaecf0" | Display | ||
| Text description of the motion of the media element. Possible values are: | | Text description of the motion of the media element. Possible values are: | ||
* "Element is projected into free flight from point of equilibrium." | * "Element is projected into free flight from point of equilibrium." | ||
| Line 487: | Line 523: | ||
|- | |- | ||
! colspan="3" style="text-align:left;" |''Trajectory'' | ! colspan="3" style="text-align:left;" |''Trajectory'' | ||
|- | |||
| ShowTrajectory | |||
| CheckBox | |||
| If enabled, the (x, y) coordinate data of the element trajectory is displayed below. | |||
|- | |- | ||
|TrajectoryData | |TrajectoryData | ||
|style="background: #eaecf0" | | |style="background: #eaecf0" | [[File:ButtonCopyToClipboard.png]] | ||
[[File: | |||
| Copies the full set of trajectory coordinates to the Windows clipboard in CSV format. | | Copies the full set of trajectory coordinates to the Windows clipboard in CSV format. | ||
|- | |- | ||
|Point, X, Y | |Point, X, Y | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
| X and Y coordinates of the media element trajectory, from the point of equilibrium to point of impact with the mill shell. | | X and Y coordinates of the media element trajectory, from the point of equilibrium to point of impact with the mill shell. Only visible if ''ShowTrajectory'' is enabled above. | ||
|} | |} | ||
Latest revision as of 07:23, 1 May 2025
Description

This article describes Powell's (1991) method for predicting the trajectory of the outer media elements in a tumbling mill.[1]
The approach predicts the point of impact of media elements projected into free flight after transit down a lifter bar surface, based on element size, lifter bar geometry, mill diameter and mill rotational speed.
The tumbling mill media trajectory model is particularly useful when combined with an estimate of charge position (e.g. Morrell's method), which allows analyses such as:
- Identifying and mitigating the risks of shell liner damage from media impact through lifter bar (or mill) design
- Monitoring trajectory and point of impact changes with charge level, mill speed or liner and lifter bar wear in operational mills
- Limiting the maximum operating speed (and hence power and throughput) in a mill simulation or process control sub-systems
Model theory
Point of equilibrium
Lifter bar tip position
Rolling
Pure rolling
Maximum angle for pure rolling
Transition to rolling and sliding
Sliding
Sliding after rolling
Pure sliding
Free-flight
Additional notes
Friction estimates
Extracting lifter geometry
Excel
The tumbling mill media trajectory model may be invoked from the Excel formula bar with the following function call:
=mdMillPower_MillMediaTrajectory(Parameters as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
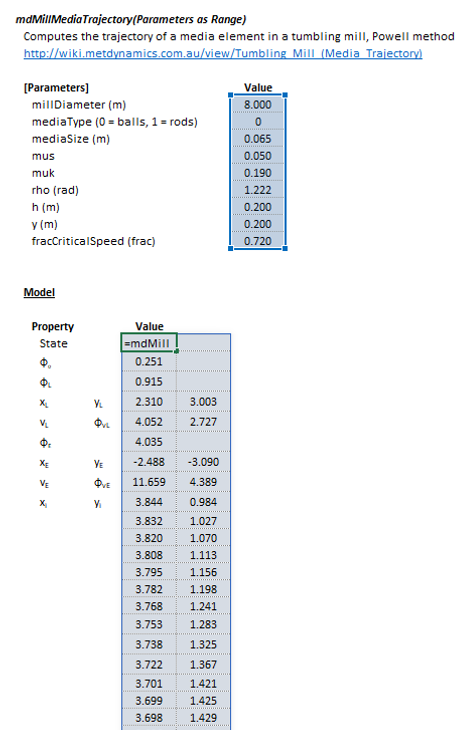
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:
and:
|
SysCAD
The media trajectory model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.
See also
References
- ↑ Powell, M.S., 1991. The effect of liner design on the motion of the outer grinding elements in a rotary mill. International Journal of Mineral Processing, 31(3-4), pp.163-193.