Tumbling Mill (Media Strings): Difference between revisions
md>Scott.Munro mNo edit summary |
imported>Scott.Munro m (→Description) |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
== Description == | |||
The article outlines a methodology for estimating the size distribution of media elements in grinding mills at recharge equilibrium, as proposed by Sepúlveda (2004):{{Sepulveda (2004)}} | |||
* The constant recharging, wearing and ejection of media elements in a mill results in a ''string'' of worn media elements of distributed sizes which descended from an original unworn (make-up) element. | |||
* Charging a mill with a mixture of new media make-up sizes results in multiple strings coexisting, and combining into an effective overall string. | |||
* When the addition rate of new media elements matches the ejection rate of scrap elements, the media strings are said to be in ''recharge equilibrium''. | |||
Sepúlveda mathematically derives an approach to estimating the mass weight by size distribution of both individual and overall combined strings at recharge equilibrium. | |||
This information may be useful for understanding the effect of changing recharge media sizes or proportions on the overall distribution of media in a mill. It may also be useful for simulation purposes, where either full media size distributions or characteristic sizes are input parameters (e.g. [[AG/SAG Mill (Variable Rates)|AG/SAG]], [[Ball Mill (Perfect Mixing)|Perfect Mixing ball mill]]). | |||
where <math>S</math> is the | == Model theory == | ||
{{Restricted content}} | |||
<hide> | |||
</hide><div class="user-show"> | |||
=== Grinding media wear kinetics === | |||
</div><hide> | |||
Sepúlveda applies a linear kinetic model to characterise the progression of media element wear. The rate of mass loss is proportional to the surface area exposed to wearing by the relation: | |||
:<math>\Omega_t = \dfrac{{\rm d} m}{{\rm d} t} = -k_{\rm m} A_{\rm b}</math> | |||
where: | |||
* <math>\Omega_t</math> is the media consumption rate (kg/h) | |||
* <math>m</math> is mass of a media element after <math>t</math> hours in the mill | |||
* <math>A_{\rm b}</math> is surface area of the media element being exposed to wear (m<sup>2</sup>) | |||
* <math>k_{\rm m}</math> is the mass wear rate constant (kg/h/m<sup>2</sup>) | |||
For spherical or cylindrical media (i.e. balls or rods), the mass rate of media consumption may be converted to a rate of change of the element diameter by: | |||
:<math>\dfrac{{\rm d} d}{{\rm d} t} = \dfrac{-2k_{\rm m}}{\rho_{\rm b}} = -k_{\rm d}</math> | |||
where: | |||
* <math>d</math> is the diameter of the grinding media element after <math>t</math> hours in the mill | |||
* <math>\rho_{\rm b}</math> is the density of the grinding media element (t/m<sup>3</sup>) | |||
* <math>k_{\rm d}</math> is the linear wear rate constant (mm/h) | |||
If the linear wear rate, <math>k_d</math>, remains constant across time, the first-order differential wear rate equation may be integrated to yield: | |||
:<math>d = d^{\rm R} - k_{\rm d}t</math> | |||
where <math>d^{\rm R}</math> is the initial size of the balls (mm), i.e. the recharge size. | |||
</hide><div class="user-show"> | |||
=== Media string size distribution === | |||
</div><hide> | |||
Sepúlveda derived a population balance relationship for the cumulative mass fraction of media elements smaller than size <math>d</math>, <math>F_3(d)</math> (w/w): | |||
:<math>F_3(d) = \dfrac {\left [ d^4 - (d^{\rm S})^4 \right ]}{\left [ (d^{\rm R})^4 - (d^{\rm S})^4 \right ]} \;\;\; \text{for } d^{\rm S} < d < d^{\rm R}</math> | |||
Discretising the size <math>d</math> into <math>n</math> intervals, each of lower size <math>d_i</math>, yields the following expression for the cumulative mass fraction of a string passing interval <math>i</math>: | |||
:<math>F_3(d_i) = \dfrac {\left [ {d_i}^4 - (d^{\rm S})^4 \right ]}{\left [ (d^{\rm R})^4 - (d^{\rm S})^4 \right ]} \;\;\; i = \left \{ 1, 2, \dots, n \right \}</math> | |||
The mass fraction retained at each size interval is therefore: | |||
:<math>f_3(d_i) = F_3(d_{i+1}) - F_3(d_{i})</math> | |||
These expressions describe the mass distribution of media by size for each individual string at recharge equilibrium. | |||
</hide><div class="user-show"> | |||
=== Specific surface area === | |||
</div><hide> | |||
The specific surface area, <math>a</math> (m<sup>2</sup>/m<sup>3</sup>), of a string is: | |||
:<math>a = 8000 (1 - f_{\rm v}) \dfrac {\left [ (d^{\rm R})^3 - (d^{\rm S})^3\right ]}{\left [ (d^{\rm R})^4 - (d^{\rm S})^4\right ]}</math> | |||
where <math>f_{\rm v} = 0.4</math> is the volumetric fraction of interstitial voids in the charge (v/v). | |||
When two different make-up ball sizes are charged to the mill, the specific surface area of the combined strings, <math>a_{\rm All}</math> (m<sup>2</sup>/m<sup>3</sup>), is: | |||
:<math>a_{\rm All} = v_1 a_1 + (1 - v_1) a_2</math> | |||
The volumetric fraction of string 1 in the mill, <math>v_1</math> (v/v), is given by: | |||
:<math>v_1 = \dfrac {r_1 a_2}{(1 - r_1) a_1 + r_1 a_2}</math> | |||
where <math>r_1</math> is the fractional composition of the string 1 recharge size in the total media recharge mass (w/w). | |||
Generalisation to <math>m</math> strings is suggested here as: | |||
:<math>a_{\rm All} = \sum_{j=1}^m v_j a_j</math> | |||
:<math>v_j = \dfrac {\prod\limits_{k=1}^{m} r_j a_k}{\sum\limits_{j=1}^{m} \left ( \prod\limits_{k=1}^{m} r_j a_k \right )}, \;\;\;\; j \neq k</math> | |||
</hide><div class="user-show"> | |||
=== Media charge size distribution === | |||
</div><hide> | |||
The overall cumulative mass fraction passing distribution of all strings in the mill is: | |||
:<math>F_3(d_i)_{\rm All} = \sum\limits_{j=1}^{m} v_j F_3(d_i)_j</math> | |||
and the overall mass fraction retined is likewise: | |||
:<math>f_3(d_i)_{\rm All} = \sum\limits_{j=1}^{m} v_j f_3(d_i)_j</math> | |||
</hide><div class="user-show"> | |||
=== Estimating scrap size === | |||
</div><hide> | |||
The scrap size (<math>d^{\rm S}</math>) from a '''grate discharge''' mill is likely to be related to size of the largest aperture in the grate, i.e. the size at which scrap balls can first be ejected. | |||
Morrell (1993) estimates the scrap size of media in an '''overflow discharge''' mill as:{{Morrell (1993)}} | |||
:<math>d^{\rm S} = 0.133 \cdot d^{\rm R} \cdot 2^{-0.25}</math> | |||
which may provide a useful estimate for media string calculations. | |||
</hide> | |||
== Excel == | |||
The grinding mill media strings model may be invoked from the Excel formula bar with the following function call: | |||
<syntaxhighlight lang="vb">=mdMillMediaStrings(Size as Range, TopSize as Range, RechargePolicy as Range, scrapSize as Double)</syntaxhighlight> | |||
{{Excel (Text, Help, No Arguments)}} | |||
The input arrays and model results are defined below in matrix notation, along with example images showing the selection of the same arrays in the Excel interface: | |||
:{| | |||
|- style="vertical-align:top;" | |||
|colspan="2"| <math> | |||
\begin{array}{l} | |||
Size = \begin{bmatrix} | |||
d_{1}\text{ (mm)}\\ | |||
\vdots\\ | |||
d_n\text{ (mm)}\\ | |||
\end{bmatrix}, & & & | |||
\begin{array}{lll} | |||
TopSize= \begin{bmatrix} | |||
{(d^{\rm R}})_{1}\text{ (mm)} & \dots & {(d^{\rm R}})_m\text{ (mm)}\\ | |||
\end{bmatrix}, & & & | |||
RechargePolicy = \begin{bmatrix} | |||
r_1\text{ (w/w)} & \dots & r_{\rm m}\text{ (w/w)}\\ | |||
\end{bmatrix} & & & | |||
scrapSize = \left [ d^{\rm S} \right ] | |||
\end{array} | |||
\end{array} | |||
</math> | |||
<math>mdMillMediaStrings = | |||
\begin{bmatrix} | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
v_1\text{ (v/v)} & \dots & v_m\text{ (v/v)}\\ | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix} \\ | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
a_1\text{ (m}^2\text{/m}^3\text{)} & \dots & a_m\text{ (m}^2\text{/m}^3\text{)}\\ | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
a_{\rm All}\text{ (m}^2\text{/m}^3\text{)} | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix}\\ | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
(P_{50})_1\text{ (mm)} & \dots & (P_{50})_m\text{ (mm)}\\ | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
(P_{50})_{\rm All}\text{ (mm)} | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
- | |||
\end{bmatrix}\\ | |||
\begin{bmatrix} | |||
\bar d_{1}\text{ (mm)}\\ | |||
\vdots\\ | |||
\bar d_n\text{ (mm)}\\ | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
F_3(d_1)_1\text{ (CFP)} & \dots & F_3(d_1)_m\text{ (CFP)}\\ | |||
\vdots & \ddots & \vdots\\ | |||
F_3(d_n)_1\text{ (CFP)} & \dots & F_3(d_n)_m\text{ (CFP)}\\ | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
F_3(d_1)_{\rm All}\text{ (CFP)}\\ | |||
\vdots\\ | |||
F_3(d_n)_{\rm All}\text{ (CFP)}\\ | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
f_3(d_1)_1\text{ (WFR)} & \dots & f_3(d_1)_m\text{ (WFR)}\\ | |||
\vdots & \ddots & \vdots\\ | |||
f_3(d_n)_1\text{ (WFR)} & \dots & f_3(d_n)_m\text{ (WFR)}\\ | |||
\end{bmatrix} & | |||
\begin{bmatrix} | |||
f_3(d_1)_{\rm All}\text{ (WFR)}\\ | |||
\vdots\\ | |||
f_3(d_n)_{\rm All}\text{ (WFR)}\\ | |||
\end{bmatrix} | |||
\end{bmatrix}\;\;\;\;\;\; | |||
</math> | |||
where <math>P_{50}</math> is the ''median size'', the 50% passing size (mm). | |||
|- style="vertical-align:top;" | |||
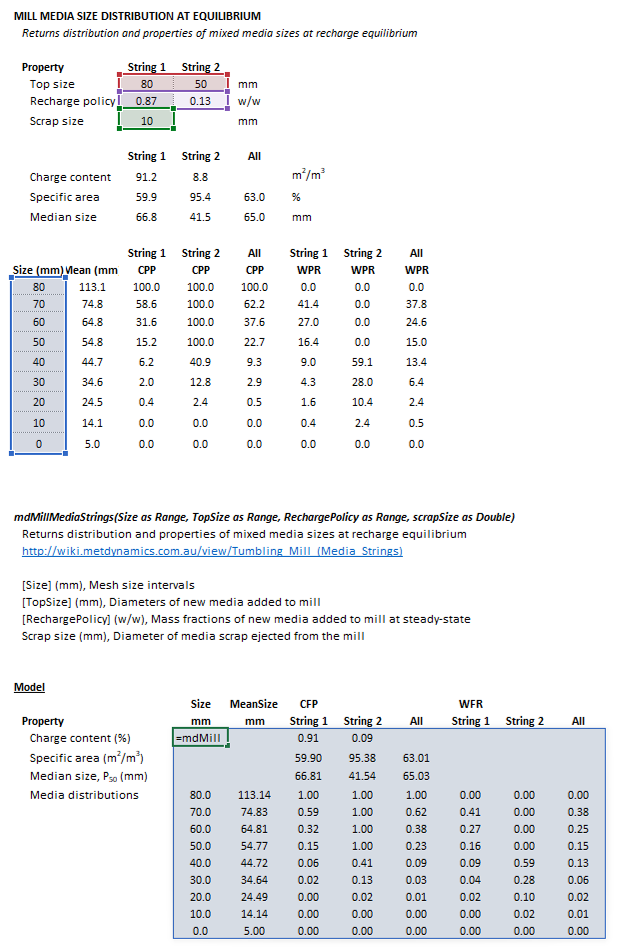
|[[File:MillMediaStrings1.png|left|frame|Figure 1. Example showing the selection of the '''Size''' (blue frame), '''TopSize''' (red frame), '''RechargePolicy''' (purple frame), '''scrapSize''' (green frame), and '''Results''' (light blue frame) arrays in Excel.]] | |||
|} | |||
== SysCAD == | |||
Media strings are an optional calculation for grinding mill units. If selected, the input and display parameters below are shown. | |||
{{SysCAD (Text, Table Header)}} | |||
|- | |||
! colspan="3" style="text-align:left;" |''MediaStrings'' | |||
{{SysCAD (Text, Help Link)}} | |||
|- | |||
! colspan="3" style="text-align:left;" |''Requirements'' | |||
|- | |||
|NumStrings | |||
| Input | |||
|Number of media strings (i.e. media recharge sizes) | |||
|- | |||
|TopSize | |||
| Input | |||
|Diameter of the recharge media by string | |||
|- | |||
|Recharge | |||
|Input | |||
|Recharge policy, fractions of each media make-up size added to the mill when recharging. | |||
|- | |||
! colspan="3" style="text-align:left;" |''Results'' | |||
|- | |||
|ChargeContent | |||
|style="background: #eaecf0" | Display | |||
|Fraction of each string in the combined charge at equilibrium. | |||
|- | |||
|SpecificArea | |||
|style="background: #eaecf0" | Display | |||
|Specific surface area of each media string and all strings combined. | |||
|- | |||
|Size | |||
|style="background: #eaecf0" | Display | |||
|Size of each interval in mesh series. | |||
|- | |||
|MedianSize | |||
|style="background: #eaecf0" | Display | |||
|Median particle diameter (P50), by string and for all strings combined. | |||
|- | |||
|MeanSize | |||
|style="background: #eaecf0" | Display | |||
|Geometric mean size of each interval in mesh series. | |||
|- | |||
|Cumulative | |||
|style="background: #eaecf0" | Display | |||
|Cumulative mass fraction passing size distribution of media at recharge equilibrium, by string and for all strings combined. | |||
|- | |||
|Retained | |||
|style="background: #eaecf0" | Display | |||
|mass fraction retained size distribution of media at recharge equilibrium, by string and for all strings combined. | |||
|} | |||
== References == | == References == | ||
[[Category:Excel]] | |||
[[Category:SysCAD]] | |||
Latest revision as of 07:26, 1 May 2025
Description
The article outlines a methodology for estimating the size distribution of media elements in grinding mills at recharge equilibrium, as proposed by Sepúlveda (2004):[1]
- The constant recharging, wearing and ejection of media elements in a mill results in a string of worn media elements of distributed sizes which descended from an original unworn (make-up) element.
- Charging a mill with a mixture of new media make-up sizes results in multiple strings coexisting, and combining into an effective overall string.
- When the addition rate of new media elements matches the ejection rate of scrap elements, the media strings are said to be in recharge equilibrium.
Sepúlveda mathematically derives an approach to estimating the mass weight by size distribution of both individual and overall combined strings at recharge equilibrium.
This information may be useful for understanding the effect of changing recharge media sizes or proportions on the overall distribution of media in a mill. It may also be useful for simulation purposes, where either full media size distributions or characteristic sizes are input parameters (e.g. AG/SAG, Perfect Mixing ball mill).
Model theory
Grinding media wear kinetics
Media string size distribution
Specific surface area
Media charge size distribution
Estimating scrap size
Excel
The grinding mill media strings model may be invoked from the Excel formula bar with the following function call:
=mdMillMediaStrings(Size as Range, TopSize as Range, RechargePolicy as Range, scrapSize as Double)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input arrays and model results are defined below in matrix notation, along with example images showing the selection of the same arrays in the Excel interface:
[math]\displaystyle{ \begin{array}{l} Size = \begin{bmatrix} d_{1}\text{ (mm)}\\ \vdots\\ d_n\text{ (mm)}\\ \end{bmatrix}, & & & \begin{array}{lll} TopSize= \begin{bmatrix} {(d^{\rm R}})_{1}\text{ (mm)} & \dots & {(d^{\rm R}})_m\text{ (mm)}\\ \end{bmatrix}, & & & RechargePolicy = \begin{bmatrix} r_1\text{ (w/w)} & \dots & r_{\rm m}\text{ (w/w)}\\ \end{bmatrix} & & & scrapSize = \left [ d^{\rm S} \right ] \end{array} \end{array} }[/math]
[math]\displaystyle{ mdMillMediaStrings = \begin{bmatrix} \begin{bmatrix} - \end{bmatrix} & \begin{bmatrix} v_1\text{ (v/v)} & \dots & v_m\text{ (v/v)}\\ \end{bmatrix} & \begin{bmatrix} - \end{bmatrix} & \begin{bmatrix} - \end{bmatrix} & \begin{bmatrix} - \end{bmatrix} \\ \begin{bmatrix} - \end{bmatrix} & \begin{bmatrix} a_1\text{ (m}^2\text{/m}^3\text{)} & \dots & a_m\text{ (m}^2\text{/m}^3\text{)}\\ \end{bmatrix} & \begin{bmatrix} a_{\rm All}\text{ (m}^2\text{/m}^3\text{)} \end{bmatrix} & \begin{bmatrix} - \end{bmatrix} & \begin{bmatrix} - \end{bmatrix}\\ \begin{bmatrix} - \end{bmatrix} & \begin{bmatrix} (P_{50})_1\text{ (mm)} & \dots & (P_{50})_m\text{ (mm)}\\ \end{bmatrix} & \begin{bmatrix} (P_{50})_{\rm All}\text{ (mm)} \end{bmatrix} & \begin{bmatrix} - \end{bmatrix} & \begin{bmatrix} - \end{bmatrix}\\ \begin{bmatrix} \bar d_{1}\text{ (mm)}\\ \vdots\\ \bar d_n\text{ (mm)}\\ \end{bmatrix} & \begin{bmatrix} F_3(d_1)_1\text{ (CFP)} & \dots & F_3(d_1)_m\text{ (CFP)}\\ \vdots & \ddots & \vdots\\ F_3(d_n)_1\text{ (CFP)} & \dots & F_3(d_n)_m\text{ (CFP)}\\ \end{bmatrix} & \begin{bmatrix} F_3(d_1)_{\rm All}\text{ (CFP)}\\ \vdots\\ F_3(d_n)_{\rm All}\text{ (CFP)}\\ \end{bmatrix} & \begin{bmatrix} f_3(d_1)_1\text{ (WFR)} & \dots & f_3(d_1)_m\text{ (WFR)}\\ \vdots & \ddots & \vdots\\ f_3(d_n)_1\text{ (WFR)} & \dots & f_3(d_n)_m\text{ (WFR)}\\ \end{bmatrix} & \begin{bmatrix} f_3(d_1)_{\rm All}\text{ (WFR)}\\ \vdots\\ f_3(d_n)_{\rm All}\text{ (WFR)}\\ \end{bmatrix} \end{bmatrix}\;\;\;\;\;\; }[/math]
where [math]\displaystyle{ P_{50} }[/math] is the median size, the 50% passing size (mm).
SysCAD
Media strings are an optional calculation for grinding mill units. If selected, the input and display parameters below are shown.
References
- ↑ Sepúlveda, J.E., 2004. Methodologies for the evaluation of grinding media consumption rates at full plant scale. Minerals engineering, 17(11-12), pp.1269-1279.