Blasting (KCO): Difference between revisions
Jump to navigation
Jump to search
imported>Scott.Munro m (→Model theory) |
imported>Scott.Munro mNo edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 5: | Line 5: | ||
== Model theory == | == Model theory == | ||
{{Restricted content}} | |||
<hide> | |||
</hide><div class="user-show"> | |||
=== Swebrec distribution === | === Swebrec distribution === | ||
</div><hide> | |||
[[File:BlastingKCO4.png|thumb|425px|Figure 1. Schematic of blast design geometry (after Bergman, 2005).{{Bergman (2005)}}]] | [[File:BlastingKCO4.png|thumb|425px|Figure 1. Schematic of blast design geometry (after Bergman, 2005).{{Bergman (2005)}}]] | ||
| Line 24: | Line 29: | ||
Figure 1 outlines the primary blast design dimensions relevant to the KCO model. | Figure 1 outlines the primary blast design dimensions relevant to the KCO model. | ||
</hide><div class="user-show"> | |||
=== Maximum block size, ''x''<sub>max</sub> === | === Maximum block size, ''x''<sub>max</sub> === | ||
</div><hide> | |||
The maximum block size is the smallest value of the ''in situ'' block size, the blast-hole burden, <math>B</math>, and the spacing, <math>S</math>, (m), i.e.: | The maximum block size is the smallest value of the ''in situ'' block size, the blast-hole burden, <math>B</math>, and the spacing, <math>S</math>, (m), i.e.: | ||
| Line 30: | Line 37: | ||
:<math>x_{\rm max} = \min \{ \textit{in}\text{ }\textit{situ}\text{ block size}, S, B \}</math> | :<math>x_{\rm max} = \min \{ \textit{in}\text{ }\textit{situ}\text{ block size}, S, B \}</math> | ||
</hide><div class="user-show"> | |||
=== Mean size parameter, ''x''<sub>50</sub> === | === Mean size parameter, ''x''<sub>50</sub> === | ||
</div><hide> | |||
The mean size of the distribution, <math>x_{50}</math> (mm), is estimated by: | The mean size of the distribution, <math>x_{50}</math> (mm), is estimated by: | ||
| Line 42: | Line 51: | ||
* <math>q</math> is the specific charge (kg/m<sup>3</sup>) | * <math>q</math> is the specific charge (kg/m<sup>3</sup>) | ||
* <math>g(n) = 1</math> is assumed | * <math>g(n) = 1</math> is assumed | ||
* The 10 factor converts Ouchterlony's '' | * The 10 factor converts Ouchterlony's ''centimeter'' units to ''millimeters''. | ||
The rock mass factor, <math>A</math> is: | The rock mass factor, <math>A</math> is: | ||
| Line 62: | Line 71: | ||
:<math>\mathit{JF} = \mathit{JPS} + \mathit{JPA}</math> | :<math>\mathit{JF} = \mathit{JPS} + \mathit{JPA}</math> | ||
where the joint plane spacing, <math>\mathit{JF}</math>, is related to the | where the joint plane spacing, <math>\mathit{JF}</math>, is related to the average joint spacing, <math>S_{\rm J}</math> (m), by: | ||
:<math>\mathit{JPS} = | :<math>\mathit{JPS} = | ||
| Line 99: | Line 108: | ||
where <math>E</math> is Young's Modulus (GPa) and <math>\sigma_{\rm c}</math> is the compressive strength of the rock (MPa). | where <math>E</math> is Young's Modulus (GPa) and <math>\sigma_{\rm c}</math> is the compressive strength of the rock (MPa). | ||
</hide><div class="user-show"> | |||
=== Curve-undulation exponent, ''b'' === | === Curve-undulation exponent, ''b'' === | ||
</div><hide> | |||
The curve-undulation exponent <math>b</math> is determined from: | The curve-undulation exponent <math>b</math> is determined from: | ||
| Line 116: | Line 127: | ||
* <math>H</math> is the bench height or hole depth (m) | * <math>H</math> is the bench height or hole depth (m) | ||
* <math>\mathit{SD}</math> is the standard deviation of drilling accuracy (m). | * <math>\mathit{SD}</math> is the standard deviation of drilling accuracy (m). | ||
</hide> | |||
== Excel == | == Excel == | ||
Latest revision as of 08:34, 1 May 2025
Description
This article describes the Kuznetsov–Cunningham–Ouchterlony (KCO) model (Ouchterlony, 2005) for predicting rock fragmentation by blasting.[1]
Model theory
 This content is available to registered users. Please log in to view.
|
Swebrec distribution
Maximum block size, xmax
Mean size parameter, x50
Curve-undulation exponent, b
Excel
The KCO blasting model may be invoked from the Excel formula bar with the following function call:
=mdUnit_Blasting_KCO(Parameters as Range, Size as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
Inputs
The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:
Results
The results are displayed in Excel as an array corresponding to the matrix notation below:
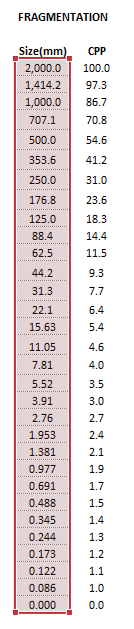
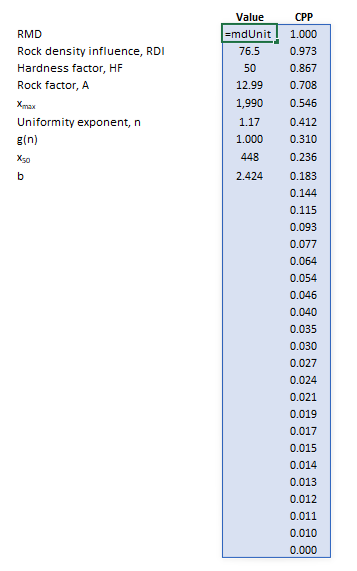
Example
The images below show the selection of input arrays and output results in the Excel interface.
 Figure 1. Example showing the selection of the Parameters (blue frame) array in Excel. |
 Figure 2. Example showing the selection of the Size (red frame) array in Excel. |
 Figure 3. Example showing the selection of the Results (light blue frame) array in Excel. |
See also
References
- ↑ Ouchterlony, F., 2005. The Swebrec© function: linking fragmentation by blasting and crushing. Mining Technology, 114(1), pp.29-44.