Tumbling Mill (Power, Hilden and Powell): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
md>Scott.Munro
m (Text replacement - "S_V" to "S_{\rm V}")
imported>Scott.Munro
 
(5 intermediate revisions by 3 users not shown)
Line 11: Line 11:
== Model theory ==
== Model theory ==


{{Restricted content}}
<hide>
Hilden and Powell's approach adopts Morrell's (1996) expression for tumbling mill power draw:{{Morrell (1996a)}}
Hilden and Powell's approach adopts Morrell's (1996) expression for tumbling mill power draw:{{Morrell (1996a)}}


Line 33: Line 36:
Sub-components of the gross power equation are described below.
Sub-components of the gross power equation are described below.


</hide><div class="user-show">
=== Charge motion power ===
=== Charge motion power ===
</div><hide>


[[File:TumblingMillPower8.png|thumb|450px|Figure 1. Tumbling mill profile showing Hilden and Powell's assumed charge and slurry component shapes when <math>U<1</math>, along with key dimensions.]]
[[File:TumblingMillPower8.png|thumb|450px|Figure 1. Tumbling mill profile showing Hilden and Powell's assumed charge and slurry component shapes when <math>U<1</math>, along with key dimensions.]]
Line 41: Line 46:
Using Morrell's (1996) equations, the power drawn by the '''charge component''' in the cylindrical and cone end sections of the mill, <math>P_{\rm L}</math> and <math>P_{\rm C}</math>, are:{{Morrell (1996a)}}
Using Morrell's (1996) equations, the power drawn by the '''charge component''' in the cylindrical and cone end sections of the mill, <math>P_{\rm L}</math> and <math>P_{\rm C}</math>, are:{{Morrell (1996a)}}


:<math>P_{\rm L} = \frac{\pi g L \rho_{\rm c} N_{\rm m} R}{3(R - zr_i)} \left [ 2R^3 -3zR^2r_i + r_i^3(3z-2) \right ].(\sin \theta_{\rm S} - \sin \theta_{\rm T}) + L \rho_{\rm c} \left ( \frac{\pi N_{\rm m} R}{R - zr_i} \right )^3 \left [ (R-zr_i)^4 - r_i^4(z-1)^4 \right ] </math>
:<math>P_{\rm L} = \frac{\pi g L \rho_{\rm c} N_{\rm m} R}{3(R - zr_{\rm i})} \left [ 2R^3 -3zR^2r_{\rm i} + r_{\rm i}^3(3z-2) \right ].(\sin \theta_{\rm S} - \sin \theta_{\rm T}) + L \rho_{\rm c} \left ( \frac{\pi N_{\rm m} R}{R - zr_{\rm i}} \right )^3 \left [ (R-zr_{\rm i})^4 - r_{\rm i}^4(z-1)^4 \right ] </math>


:<math>P_{\rm C} = \frac{\pi g L_{\rm d} \rho_{\rm c} N_{\rm m}}{3(R-r_{\rm T})}(R^4 - 4Rr_i^3 + 3r_i^4)(\sin \theta_{\rm S} - \sin \theta_{\rm T}) + \frac{2 \pi^3 N_{\rm m}^3 L_{\rm d} \rho_{\rm c}}{5(R-r_{\rm T})}(R^5 - 5Rr_i^4 + 4r_i^5)</math>
:<math>P_{\rm C} = \frac{\pi g L_{\rm d} \rho_{\rm c} N_{\rm m}}{3(R-r_{\rm T})}(R^4 - 4Rr_{\rm i}^3 + 3r_{\rm i}^4)(\sin \theta_{\rm S} - \sin \theta_{\rm T}) + \frac{2 \pi^3 N_{\rm m}^3 L_{\rm d} \rho_{\rm c}}{5(R-r_{\rm T})}(R^5 - 5Rr_{\rm i}^4 + 4r_{\rm i}^5)</math>


where:
where:
Line 53: Line 58:
* <math>R</math> is the mill radius inside liners (m), which is half the mill diameter <math>D</math>, i.e. <math>R=0.5D</math>
* <math>R</math> is the mill radius inside liners (m), which is half the mill diameter <math>D</math>, i.e. <math>R=0.5D</math>
* <math>r_{\rm T}</math> is the trunnion radius inside liners (m), which is half the trunnion diameter <math>d_{\rm T}</math>, i.e. <math>r_{\rm T}=0.5d_{\rm T}</math>
* <math>r_{\rm T}</math> is the trunnion radius inside liners (m), which is half the trunnion diameter <math>d_{\rm T}</math>, i.e. <math>r_{\rm T}=0.5d_{\rm T}</math>
* <math>r_i</math> is the inner surface radius of the charge (m)
* <math>r_{\rm i}</math> is the inner surface radius of the charge (m)
* <math>\theta_{\rm S}</math> is the angle of the charge shoulder (radians)
* <math>\theta_{\rm S}</math> is the angle of the charge shoulder (radians)
* <math>\theta_{\rm T}</math> is the angle of the charge toe (radians)
* <math>\theta_{\rm T}</math> is the angle of the charge toe (radians)
Line 72: Line 77:
where <math>J_{\rm T}</math> is the total mill filling of balls plus rocks (v/v).
where <math>J_{\rm T}</math> is the total mill filling of balls plus rocks (v/v).


The power drawn by the '''slurry component''' in the cylindrical and cone end sections, <math>P'_{\rm L}</math> and <math>P'_{\rm C}</math>, is computed by substituting the slurry component properties <math>\rho'_c</math>, <math>r'_i</math>, <math>z'</math>, and <math>\theta_{\rm L}</math> for the equivalent charge properties <math>\rho_{\rm c}</math>, <math>r_i</math>, <math>z</math>, and <math>\theta_{\rm T}</math> in the same equations for <math>P_{\rm L}</math> and <math>P_{\rm C}</math>, where:
The power drawn by the '''slurry component''' in the cylindrical and cone end sections, <math>P'_{\rm L}</math> and <math>P'_{\rm C}</math>, is computed by substituting the slurry component properties <math>\rho'_c</math>, <math>r'_{\rm i}</math>, <math>z'</math>, and <math>\theta_{\rm L}</math> for the equivalent charge properties <math>\rho_{\rm c}</math>, <math>r_{\rm i}</math>, <math>z</math>, and <math>\theta_{\rm T}</math> in the same equations for <math>P_{\rm L}</math> and <math>P_{\rm C}</math>, where:
* <math>\rho'_c</math> is the density of the slurry component in the mill (t/m<sup>3</sup>)
* <math>\rho'_c</math> is the density of the slurry component in the mill (t/m<sup>3</sup>)
* <math>r'_i</math> is the inner surface radius of the slurry component (m)
* <math>r'_{\rm i}</math> is the inner surface radius of the slurry component (m)
* <math>z'</math> is an empirical term that relates the rotational rate of mass at radial positions within the slurry component to the rotational rate of the mill
* <math>z'</math> is an empirical term that relates the rotational rate of mass at radial positions within the slurry component to the rotational rate of the mill
* <math>\theta_{\rm L}</math> is the angle of the toe of the slurry component (radians)
* <math>\theta_{\rm L}</math> is the angle of the toe of the slurry component (radians)
Line 96: Line 101:
The remaining parameters of the charge motion power equations are described below.
The remaining parameters of the charge motion power equations are described below.


</hide><div class="user-show">
=== Charge position ===
=== Charge position ===
</div><hide>


The charge shoulder and toe positions and inner surface radius are calculated using Morrell's (1996) method.{{Morrell (1996a)}}
The charge shoulder and toe positions and inner surface radius are calculated using Morrell's (1996) method.{{Morrell (1996a)}}
Line 117: Line 124:
:<math>\theta_{\rm S} = \frac{\pi}{2} - \left ( \theta_{\rm T} - \frac{\pi}{2} \right ) \big[ \left ( 0.336 + 0.1041 \phi \right ) + \left (1.54 - 2.5673 \phi \right ) J_{\rm T} \big]</math>
:<math>\theta_{\rm S} = \frac{\pi}{2} - \left ( \theta_{\rm T} - \frac{\pi}{2} \right ) \big[ \left ( 0.336 + 0.1041 \phi \right ) + \left (1.54 - 2.5673 \phi \right ) J_{\rm T} \big]</math>


The inner surface '''radius of the charge''', <math>r_i</math> (m) is:
The inner surface '''radius of the charge''', <math>r_{\rm i}</math> (m) is:


:<math>r_i = R \sqrt{1 - \frac{2 \pi \beta J_{\rm T}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}}}</math>
:<math>r_{\rm i} = R \sqrt{1 - \frac{2 \pi \beta J_{\rm T}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}}}</math>


where the active load fraction, <math>\beta</math> (frac), is:
where the active load fraction, <math>\beta</math> (frac), is:
Line 125: Line 132:
:<math>\beta = \frac{\left ( \dfrac{2 \pi + \theta_{\rm S} - \theta_{\rm T}}{\pi N_{\rm m}} \right )}{\sqrt{\dfrac{R}{g} \left ( 1 + \sqrt{1 - \dfrac{2 \pi J_{\rm T}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}} } \right ) (\sin \theta_{\rm S} - \sin \theta_{\rm T})} + \left( \dfrac{2 \pi + \theta_{\rm S} - \theta_{\rm T}}{\pi N_{\rm m}} \right )}</math>
:<math>\beta = \frac{\left ( \dfrac{2 \pi + \theta_{\rm S} - \theta_{\rm T}}{\pi N_{\rm m}} \right )}{\sqrt{\dfrac{R}{g} \left ( 1 + \sqrt{1 - \dfrac{2 \pi J_{\rm T}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}} } \right ) (\sin \theta_{\rm S} - \sin \theta_{\rm T})} + \left( \dfrac{2 \pi + \theta_{\rm S} - \theta_{\rm T}}{\pi N_{\rm m}} \right )}</math>


</hide><div class="user-show">
=== Slurry position ===
=== Slurry position ===
</div><hide>


The position of the '''shoulder of the slurry component''' is the same as the charge shoulder position.  
The position of the '''shoulder of the slurry component''' is the same as the charge shoulder position.  
Line 133: Line 142:
* if <math>U>1</math> then there is an excess of slurry beyond the available charge void space, which manifests as a slurry pool, and <math>\theta_{\rm L} < \theta_{\rm T}</math>.
* if <math>U>1</math> then there is an excess of slurry beyond the available charge void space, which manifests as a slurry pool, and <math>\theta_{\rm L} < \theta_{\rm T}</math>.


</hide><div class="user-show">
==== Slurry toe when U≤1 ====
==== Slurry toe when U≤1 ====
</div><hide>


When the charge void space is partially or exactly filled with slurry (<math>U\leq1</math>), the position of the '''toe of the slurry component''', <math>\theta_{\rm L}</math> (rad), is:
When the charge void space is partially or exactly filled with slurry (<math>U\leq1</math>), the position of the '''toe of the slurry component''', <math>\theta_{\rm L}</math> (rad), is:
Line 141: Line 152:
where <math>y</math> is the profile shape factor (frac).
where <math>y</math> is the profile shape factor (frac).


The inner surface '''radius of the slurry component''', <math>r'_i</math> (m), is:
The inner surface '''radius of the slurry component''', <math>r'_{\rm i}</math> (m), is:


:<math>r'_i = \sqrt{R^2 - \frac{U(R^2-r_i^2).(2\pi+\theta_{\rm S}-\theta_{\rm T})}{2\pi+\theta_{\rm S}-\theta_{\rm L}}}</math>
:<math>r'_{\rm i} = \sqrt{R^2 - \frac{U(R^2-r_{\rm i}^2).(2\pi+\theta_{\rm S}-\theta_{\rm T})}{2\pi+\theta_{\rm S}-\theta_{\rm L}}}</math>


</hide><div class="user-show">
==== Slurry toe when U>1 ====
==== Slurry toe when U>1 ====
</div><hide>


[[File:TumblingMillPower9.png|thumb|450px|Figure 3. Tumbling mill profile showing Hilden and Powell's assumed charge and slurry component shapes when <math>U>1</math>, along with key dimensions and areas.]]
[[File:TumblingMillPower9.png|thumb|450px|Figure 3. Tumbling mill profile showing Hilden and Powell's assumed charge and slurry component shapes when <math>U>1</math>, along with key dimensions and areas.]]


[[File:TumblingMillPower10.png|thumb|450px|Figure 4. Tumbling mill profile showing Hilden and Powell's assumed charge and slurry component shapes when <math>U>1</math>, <math>h<r_i</math> and <math>h_2<r_i</math>, along with key dimensions and areas.]]
[[File:TumblingMillPower10.png|thumb|450px|Figure 4. Tumbling mill profile showing Hilden and Powell's assumed charge and slurry component shapes when <math>U>1</math>, <math>h<r_{\rm i}</math> and <math>h_2<r_{\rm i}</math>, along with key dimensions and areas.]]


When the charge void space is overfilled (<math>U>1</math>), a slurry pool forms.  
When the charge void space is overfilled (<math>U>1</math>), a slurry pool forms.  
Line 159: Line 172:
Only the slurry in the annular sector (<math>A_{\rm Sect}</math>) contributes to power draw.  
Only the slurry in the annular sector (<math>A_{\rm Sect}</math>) contributes to power draw.  


The inner surface '''radius of the slurry component''' filling the charge void space and extending into the annular sector is equal to the charge radius, i.e. <math>r'_i = r_i</math>.
The inner surface '''radius of the slurry component''' filling the charge void space and extending into the annular sector is equal to the charge radius, i.e. <math>r'_{\rm i} = r_{\rm i}</math>.


Locating the position of the '''toe of the slurry component''', <math>\theta_{\rm L}</math>, then becomes a problem of determining the distribution of slurry between the two areas, <math>A_{\rm Seg}</math> and <math>A_{\rm Sect}</math>.
Locating the position of the '''toe of the slurry component''', <math>\theta_{\rm L}</math>, then becomes a problem of determining the distribution of slurry between the two areas, <math>A_{\rm Seg}</math> and <math>A_{\rm Sect}</math>.
Line 165: Line 178:
The total area of excess slurry, <math>A_x</math> (m<sup>2</sup>), in the pool is:
The total area of excess slurry, <math>A_x</math> (m<sup>2</sup>), in the pool is:


:<math>A_x = A_{\rm Seg} + A_{\rm Sect} = (U - 1) . \frac{1}{2} (R^2 - r_i^2).(2 \pi + \theta_{\rm S} - \theta_{\rm T})</math>
:<math>A_x = A_{\rm Seg} + A_{\rm Sect} = (U - 1) . \frac{1}{2} (R^2 - r_{\rm i}^2).(2 \pi + \theta_{\rm S} - \theta_{\rm T})</math>


The area of the annular segment, <math>A_{\rm Seg}</math>, is:
The area of the annular segment, <math>A_{\rm Seg}</math>, is:
Line 171: Line 184:
:<math>A_{\rm Seg} =  
:<math>A_{\rm Seg} =  
\begin{cases}
\begin{cases}
r_i^2 . \arccos \left ( \frac{h}{r_i} \right ) - h . \sqrt{r_i^2 - h^2} & \text{if }h<r_i\\
r_{\rm i}^2 . \arccos \left ( \frac{h}{r_{\rm i}} \right ) - h . \sqrt{r_{\rm i}^2 - h^2} & \text{if }h<r_{\rm i}\\
\left ( r_i^2.\arccos \left ( \frac{h}{r_i} \right ) - h.\sqrt{r_i^2 - h^2} \right ) - \left ( r_i^2.\arccos \left ( \frac{h_2}{r_i} \right ) - h_2.\sqrt{r_i^2 - h_2^2} \right ) & \text{if }h<r_i \text{ and }h_2<r_i
\left ( r_{\rm i}^2.\arccos \left ( \frac{h}{r_{\rm i}} \right ) - h.\sqrt{r_{\rm i}^2 - h^2} \right ) - \left ( r_{\rm i}^2.\arccos \left ( \frac{h_2}{r_{\rm i}} \right ) - h_2.\sqrt{r_{\rm i}^2 - h_2^2} \right ) & \text{if }h<r_{\rm i} \text{ and }h_2<r_{\rm i}
\end{cases}
\end{cases}
</math>
</math>
Line 178: Line 191:
where the parameters <math>h</math> and <math>h_2</math>, as shown in Figure 4, are:
where the parameters <math>h</math> and <math>h_2</math>, as shown in Figure 4, are:


:<math>h = - \left ( \frac{R + r_i}{2} \right ) . \sin \theta_{\rm L}</math>
:<math>h = - \left ( \frac{R + r_{\rm i}}{2} \right ) . \sin \theta_{\rm L}</math>


:<math>h_2 = - \left ( \frac{R + r_i}{2} \right ) . \sin \theta_{\rm T}</math>
:<math>h_2 = - \left ( \frac{R + r_{\rm i}}{2} \right ) . \sin \theta_{\rm T}</math>


The area of the circular sector, <math>A_{\rm Sect}</math>, is:
The area of the circular sector, <math>A_{\rm Sect}</math>, is:


:<math>A_{\rm Sect} = \frac{(\theta_{\rm T} - \theta_{\rm L}}{2} . (R^2 - r_i^2)</math>
:<math>A_{\rm Sect} = \frac{(\theta_{\rm T} - \theta_{\rm L}}{2} . (R^2 - r_{\rm i}^2)</math>


The slurry toe parameter <math>\theta_{\rm L}</math> cannot be algebraically isolated in the above equations. Therefore, an iterative numerical method is used to solve the value of <math>\theta_{\rm L}</math> that yields the required value of <math>A_x</math> (in this case, [https://en.wikipedia.org/wiki/Ridders%27_method Ridders' method]).
The slurry toe parameter <math>\theta_{\rm L}</math> cannot be algebraically isolated in the above equations. Therefore, an iterative numerical method is used to solve the value of <math>\theta_{\rm L}</math> that yields the required value of <math>A_x</math>.


</hide><div class="user-show">
=== Charge density ===
=== Charge density ===
</div><hide>


The masses of balls, <math>m_{\rm B}</math> (t), and coarse rocks, <math>m_{\rm R}</math> (t), in the charge are:
The masses of balls, <math>m_{\rm B}</math> (t), and coarse rocks, <math>m_{\rm R}</math> (t), in the charge are:
Line 198: Line 213:
where:
where:
* <math>J_{\rm B}</math> is the ball filling (v/v)
* <math>J_{\rm B}</math> is the ball filling (v/v)
* <math>V_{\rm C}</math> is the volume of of the cylindrical section of the mill (m<sup>3</sup>)
* <math>V_{\rm C}</math> is the volume of the cylindrical section of the mill (m<sup>3</sup>)
* <math>\varepsilon</math> is the charge void fraction, typically 0.4 (v/v)
* <math>\varepsilon</math> is the charge void fraction, typically 0.4 (v/v)
* <math>\rho_{\rm B}</math> is the Specific Gravity or density of the balls (- or t/m<sup>3</sup>)
* <math>\rho_{\rm B}</math> is the Specific Gravity or density of the balls (- or t/m<sup>3</sup>)
Line 222: Line 237:


:<math>S_{\rm V} = \frac{S}{\rho_{\rm R} \left ( \dfrac{S}{\rho_{\rm R}} + \dfrac{1 - S}{\rho_{\rm L}} \right )}</math>
:<math>S_{\rm V} = \frac{S}{\rho_{\rm R} \left ( \dfrac{S}{\rho_{\rm R}} + \dfrac{1 - S}{\rho_{\rm L}} \right )}</math>
</hide><div class="user-show">


=== No-load power ===
=== No-load power ===
</div><hide>


The no-load power (<math>P_{\rm N}</math>) is estimated as:
The no-load power (<math>P_{\rm N}</math>) is estimated as:
Line 258: Line 276:
| 6.1
| 6.1
|}
|}
</hide>


== Excel ==
== Excel ==
Line 301: Line 320:
\theta_{\rm T} \text{ (rad)}\\
\theta_{\rm T} \text{ (rad)}\\
\theta_{L} \text{ (rad)}\\
\theta_{L} \text{ (rad)}\\
r_i\text{ (m)}\\
r_{\rm i}\text{ (m)}\\
r'_i\text{ (m)}\\
r'_{\rm i}\text{ (m)}\\
\end{bmatrix}\;\;\;\;\;\;
\end{bmatrix}\;\;\;\;\;\;
</math>
</math>

Latest revision as of 08:15, 1 May 2025

Description

This article describes the Hilden and Powell (2018) approach for estimating the power draw of a tumbling mill.[1]

Hilden and Powell extended Morrell's (1996, 2016) approaches to include the following features:[2][3]

  • Partial filling of the charge void space with slurry in two directions, from the charge shoulder towards the toe and from the outer shell towards the mill centre
  • Estimation of the fraction of a slurry pool which settles across the centre of the mill profile and thus does not contribute to power draw
  • No-load power based on mill drive type and size

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Charge motion power

Charge position

Slurry position

Slurry toe when U≤1

Slurry toe when U>1

Charge density

No-load power

Excel

The Hilden and Powell mill power model may be invoked from the Excel formula bar with the following function call: 

=mdMillPower_HildenPowell(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

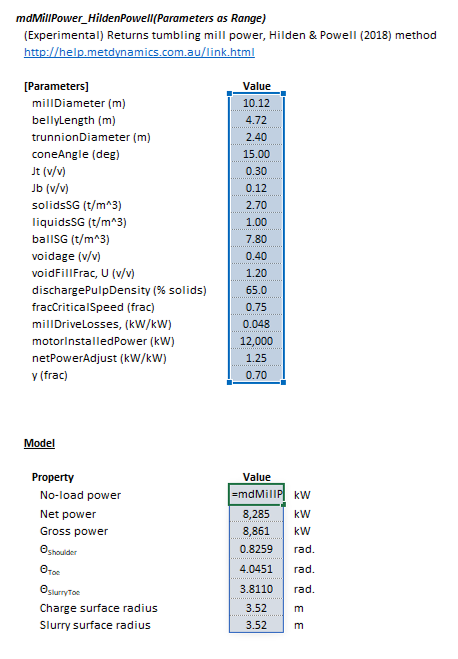
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:


where:

Figure 5. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Hilden and Powell power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
HildenPowell
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
MillDiameter Display Diameter of the mill (inside liners).
BellyLength Display Length of the cylindrical section (belly) of the mill (inside liners).
TrunnionDiameter Display Diameter of the trunnion (inside liners).
ConeAngle Display Angular displacement of the cone surface from the vertical direction.
Jt Display Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
BallLoadVol Display Volumetric fraction of the mill occupied by balls (including voids).
SolidsSG Display Specific Gravity or density of solids.
BallSG Display Specific Gravity or density of balls.
LiquidsSG Display Specific Gravity or density of liquids.
Voidage Input/Display Volumetric fraction of interstitial void space in the charge. Usually 0.4.
Note: The Dynamic Perfect Mixing ball mill model uses Shi's dynamic charge porosity estimation to align power draw predictions with the adopted slurry filling approach.
U Display Volumetric fraction of interstitial grinding media voidage occupied by slurry.
Cw Display Mass fraction of solids in discharge slurry.
FracCS Display Fraction critical speed of the mill.
MillDriveLosses Input Mill drive motor power loss factor.
MotorInstalledPower Input Maximum power draw of installed mill motor.
NetPowerAdjust Input Lumped calibration parameter accounting for power losses. Found to be a value of 1.26 for industrial mills.
y Input Profile shape factor.
ThetaShoulder Display Angle of the charge shoulder.
ThetaToe Display Angle of the charge toe.
ThetaSlurryToe Display Angle of the toes of the slurry component
ChargeSurfaceRadius Display Radius of the inner surface of the charge.
SlurrySurfaceRadius Display Radius of the inner surface of the slurry component.
NoLoadPower Display Power input to the motor when the mill is empty (no balls, rocks or slurry).
NetPower Display Charge motion power, including losses.
GrossPower Display Power input to the motor.

See also

References

  1. ↑ Hilden, M.M. and Powell, M.S., 2018. A model of SAG mill power incorporating slurry filling and its application to real-time mill performance analysis. Paper presented at Comminution '18, Cape Town, South Africa, April 16-19, 2018.
  2. ↑ Morrell, S., 1996. Power draw of wet tumbling mills and its relationship to charge dynamics. Pt. 1: a continuum approach to mathematical modelling of mill power draw. Transactions of the Institution of Mining and Metallurgy. Section C. Mineral Processing and Extractive Metallurgy, 105.
  3. ↑ Morrell, S., 2016. Modelling the influence on power draw of the slurry phase in Autogenous (AG), Semi-autogenous (SAG) and ball mills. Minerals Engineering, 89, pp.148-156.
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Tumbling_Mill_(Power,_Hilden_and_Powell)&oldid=2463"