Properties (Bulk Density): Difference between revisions
Jump to navigation
Jump to search
Scott Munro (talk | contribs) m (1 revision imported) |
imported>Scott.Munro m (→Model theory) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Description == | == Description == | ||
This article describes the Evertsson (1999) method for estimating the bulk density of a polydisperse particle ensemble.{{Evertsson (1999)}} | This article describes the Evertsson (1999) method for estimating the dry bulk density of a polydisperse particle ensemble.{{Evertsson (1999)}} | ||
The Evertsson method was derived for cone crusher products, but the relationships may also be applicable in similar mineral processing and materials handling contexts, e.g. conveyors and bins, screen or HPGR feed etc. | |||
== Model theory == | == Model theory == | ||
{{ | {{Restricted content}} | ||
<hide> | |||
The bulk density of a particle assembly is defined as the total mass divided by the bulk volume it occupies, where bulk volume includes both the volume of particles and the empty, void space between them. | |||
The distribution of particle mass by size has a significant impact on the overall bulk density of an assembly: | |||
* A particle size distribution which has a "wide spread" will have even fractions of both coarse and fine particles - the fine particles are able to occupy the many interstitial void spaces between the larger particles, and the overall bulk density is high. | |||
* In a "narrow" particle size distribution, the majority of particles are of approximately the same size - there are few small particles available to fit within the void space, and the bulk density is low. | |||
Evertsson (1999) proposed an empirical relationship which links bulk density to the size distribution of particles.{{Evertsson (1999)}} | |||
The notional "spread" of a particle size distribution is first reduced to the statistical measures of mean size (<math>\bar x</math>) and standard deviation (<math>\sigma</math>): | |||
:<math> | |||
\begin{array}{ccc} | |||
\bar x = \sum\limits_{i=1}^{n} f_i \bar d_i & & \sigma = \sum\limits_{i=1}^{n} f_i (\bar d_i - \bar x)^2\\ | |||
\end{array} | |||
</math> | |||
where: | |||
* <math>n</math> is the number of size intervals | |||
* <math>f_i</math> is the fraction of total particle volume in size interval <math>i</math> (w/w), <math display="inline"> \sum_{i=1}^{n} f_i = 1</math> | |||
* <math>\bar d_{i}</math> is the [[Conversions|geometric mean size]] of particles in size interval <math>i</math> (mm) | |||
The standard deviation is normalised to a dimensionless standard deviation (<math>\sigma_{\aleph}</math>): | |||
:<math> | |||
\begin{array}{ccc} | |||
\sigma_{\aleph} = \dfrac{\sigma}{\bar x}, & & 0 \leq \sigma_{\aleph} \leq 1 | |||
\end{array} | |||
</math> | |||
Evertsson fitted a polynomial function to bulk density and size distribution data from full-scale crushing tests to yield the following expression for ''normalised density'', <math>\rho_{\aleph}</math> (v/v), otherwise described as the "packing fraction" or solids volume fraction: | |||
:<math>\rho_{\aleph} = D_1 {\sigma_{\aleph}}^3 + D_2 {\sigma_{\aleph}}^2 + \rho_{\aleph, \rm mono}</math> | |||
with | |||
:<math> | |||
\begin{array}{ccc} | |||
D_1 = -0.062277, & D_2 = 0.24758, & \rho_{\aleph, \rm mono} = 0.54284\\ | |||
\end{array} | |||
</math> | |||
The actual bulk density, <math>\rho_{\rm Bulk}</math> (t/m<sup>3</sup>), of an assembly of particles consisting of materials or minerals of differing density can be derived as: | |||
:<math>\rho_{\rm Bulk} = \dfrac{M}{\left ( \dfrac{V}{\rho_{\aleph}} \right )} = \rho_{\aleph} . \left ( \dfrac{M}{V} \right )</math> | |||
where <math>M</math> and <math>V</math> are the total mass (t) and total volume (m<sup>3</sup>) of particles of all sizes and densities in the assembly, respectively. | |||
The total mass and total volume can be determined from the following expressions: | |||
:<math>M = \sum_{i=1}^{n} \sum_{j=1}^{m} (Q_{\rm M})_{ij}</math> | |||
:<math>V = \sum\limits_{i=1}^{n} \left ( \dfrac{\sum_{j=1}^{m} (Q_{\rm M})_{ij}}{(\rho_S)_{j}} \right )</math> | |||
where: | |||
* <math>m</math> is the number of ore types, minerals, density classes etc. | |||
* <math>Q_{\rm M}</math> is the mass flow rate of particles in the stream (t/h) | |||
* <math>\rho_{\rm S}</math> is the Specific Gravity or density of solids (- or t/m<sup>3</sup>) | |||
</hide> | |||
== Excel == | == Excel == | ||
| Line 48: | Line 110: | ||
\mathit{mdProps\_BulkDensity\_Evertsson} = | \mathit{mdProps\_BulkDensity\_Evertsson} = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
\rho_{\rm | \rho_{\rm Bulk}\text{ (t/m}^\text{3}\text{)}^*\text{ or } \rho_{\aleph}\text{ (v/v)}^*\\ | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|- style="vertical-align:top;" | |- style="vertical-align:top;" | ||
|colspan="2"| | |colspan="2"| | ||
where: | where: | ||
* <math>\mathit{returnPackFrac}</math> indicates whether to return the packing fraction (i.e. solids volume fraction, <math>\rho_{\aleph}</math>) of particles in the stream (v/v). Default is to return the bulk density (t/m<sup>3</sup>) | |||
* <math>\ | |||
* the superscript <math>^*</math> indicates an optionally-returned value | * the superscript <math>^*</math> indicates an optionally-returned value | ||
|} | |} | ||
| | | | ||
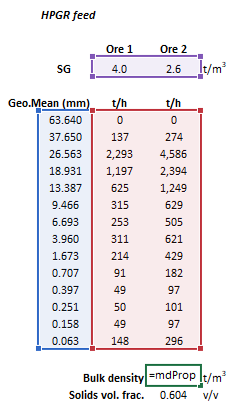
:[[File:PropsBulkDensity1.png|frame|Figure 1. Example showing the selection of the '''MeanSize''' (blue frame), '''Stream''' (red frame), '''SG''' (purple frame), and Results (green frame) arrays in Excel | :[[File:PropsBulkDensity1.png|frame|Figure 1. Example showing the selection of the '''MeanSize''' (blue frame), '''Stream''' (red frame), '''SG''' (purple frame), and Results (green frame) arrays in Excel.]] | ||
|} | |} | ||
Latest revision as of 11:27, 4 December 2024
Description
This article describes the Evertsson (1999) method for estimating the dry bulk density of a polydisperse particle ensemble.[1]
The Evertsson method was derived for cone crusher products, but the relationships may also be applicable in similar mineral processing and materials handling contexts, e.g. conveyors and bins, screen or HPGR feed etc.
Model theory
 This content is available to registered users. Please log in to view.
|
Excel
The Evertsson bulk density estimation may be invoked from the Excel formula bar with the following function call:
=mdProps_BulkDensity_Evertsson(MeanSize as Range, Stream as Range, SG as Range, Optional returnPackFrac as Boolean = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
![{\displaystyle {\begin{aligned}MeanSize&={\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{31}{\text{ (mm)}}\\\end{bmatrix}}\\\\{\mathit {Stream}}&={\begin{bmatrix}(Q_{\rm {M}})_{11}{\text{ (t/h)}}&\dots &(Q_{\rm {M}})_{1m}{\text{ (t/h)}}\\\vdots &\ddots &\vdots \\(Q_{\rm {M}})_{n1}{\text{ (t/h)}}&\dots &(Q_{\rm {M}})_{nm}{\text{ (t/h)}}\\\end{bmatrix}}\\\\{\mathit {SG}}&={\begin{bmatrix}(\rho _{\rm {S}})_{1}{\text{ (t/m}}^{\text{3}}{\text{)}}&\dots &(\rho _{\rm {S}})_{m}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\end{bmatrix}}\\\\{\mathit {returnPackFrac}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6d00b61b361e569269897963673990616be01b8)
References
- ↑ Evertsson, C.M., 1999. Size reduction in cone crushers. In Minerals Engineering Conference '99, Falmouth, England, 22-24 September 1999.