Tumbling Mill (Power, Morrell Discrete Shell): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
m (1 revision imported)
imported>Scott.Munro
mNo edit summary
 
(7 intermediate revisions by 3 users not shown)
Line 8: Line 8:
== Model theory ==
== Model theory ==


{{Restricted content}}
<hide>
[[File:TumblingMillPower5.png|thumb|700px|thumb|Figure 1. Grate discharge tumbling mill profile illustrating the Morrell D model's charge shape and concentric shell layers (at increments of five for clarity).<br><br>The radial position (<math>r</math>), shoulder position (<math>\theta_{S25}</math>) and toe position (<math>\theta_{T25}</math>) of shell 25 are shown as an example.]]
[[File:TumblingMillPower5.png|thumb|700px|thumb|Figure 1. Grate discharge tumbling mill profile illustrating the Morrell D model's charge shape and concentric shell layers (at increments of five for clarity).<br><br>The radial position (<math>r</math>), shoulder position (<math>\theta_{S25}</math>) and toe position (<math>\theta_{T25}</math>) of shell 25 are shown as an example.]]


Line 20: Line 23:
The power imparted to each shell is therefore different, and the total power input to the motor of a tumbling mill is then:
The power imparted to each shell is therefore different, and the total power input to the motor of a tumbling mill is then:


:<math>\text{Gross power (kW)} = \text{No-load power} + \sum_{i=1}^{n}{P_r}</math>
:<math>\text{Gross power (kW)} = \text{No-load power} + \sum_{i=1}^{n}{P_{\rm r}}</math>


where <math>P_r</math> is the power draw of discrete shell <math>i</math>, and <math>n</math> is the number of shells comprising the charge.
where <math>P_{\rm r}</math> is the power draw of discrete shell <math>i</math>, and <math>n</math> is the number of shells comprising the charge.


=== Power per shell ===
=== Power per shell ===
Line 30: Line 33:
:<math>
:<math>
\begin{align}
\begin{align}
P_r & = 2 \pi \int_{r - \bar x}^{r} \int_{\theta_{Tr}}^{\theta_{Sr}} N_r r^2 L \rho_c g \cos \theta \, {\rm d} \theta \, {\rm d} r + 4 \pi^3 \int_{r - \bar x}^{r} N_r^3 r^3 L \rho_c \, {\rm d}r + 2 \pi \int_{r - \bar x}^{r} \int_{\theta_{TO}}^{\theta_{Tr}} N_r R^2 L \rho_p g \cos \theta \, {\rm d} \theta \, {\rm d}r\\
P_{\rm r} & = 2 \pi \int_{r - \bar x}^{r} \int_{\theta_{{\rm T}r}}^{\theta_{{\rm S}r}} N_r r^2 L \rho_{\rm c} g \cos \theta \, {\rm d} \theta \, {\rm d} r + 4 \pi^3 \int_{r - \bar x}^{r} N_r^3 r^3 L \rho_{\rm c} \, {\rm d}r + 2 \pi \int_{r - \bar x}^{r} \int_{\theta_{\rm TO}}^{\theta_{{\rm T}r}} N_r R^2 L \rho_{\rm p} g \cos \theta \, {\rm d} \theta \, {\rm d}r\\
& = \frac{2}{3} \pi LgN_r \left (r^3 - (r - \bar x)^3 \right ) \left ( \rho_c (\sin \theta_{Sr} - \sin \theta_{Tr}) + \rho_p (\sin \theta_{Tr} - \sin \theta_{TO}) \right ) + \pi^3 L \rho_c N_r^3 \left ( r^4 - (r - \bar x)^4 \right )
& = \frac{2}{3} \pi LgN_r \left (r^3 - (r - \bar x)^3 \right ) \left ( \rho_{\rm c} (\sin \theta_{{\rm S}r} - \sin \theta_{{\rm T}r}) + \rho_{\rm p} (\sin \theta_{{\rm T}r} - \sin \theta_{\rm TO}) \right ) + \pi^3 L \rho_{\rm c} N_r^3 \left ( r^4 - (r - \bar x)^4 \right )
\end{align}
\end{align}
</math>
</math>
Line 40: Line 43:
* <math>N_r</math> is the rotational rate at radial position <math>r</math> (revs/s)
* <math>N_r</math> is the rotational rate at radial position <math>r</math> (revs/s)
* <math>L</math> is the mill length of cylindrical section (m)
* <math>L</math> is the mill length of cylindrical section (m)
* <math>\rho_c</math> is the  charge density (t/m<sup>3</sup>)
* <math>\rho_{\rm c}</math> is the  charge density (t/m<sup>3</sup>)
* <math>\rho_p</math> is the discharge pulp density (t/m<sup>3</sup>)
* <math>\rho_{\rm p}</math> is the discharge pulp density (t/m<sup>3</sup>)
* <math>\theta_{Sr}</math> is the shoulder angle at radial position <math>r</math> (rad)
* <math>\theta_{{\rm S}r}</math> is the shoulder angle at radial position <math>r</math> (rad)
* <math>\theta_{Tr}</math> is the toe angle at radial position <math>r</math> (rad)
* <math>\theta_{{\rm T}r}</math> is the toe angle at radial position <math>r</math> (rad)
* <math>\theta_{TO}</math> is the slurry pool overflow angle (rad)
* <math>\theta_{\rm TO}</math> is the slurry pool overflow angle (rad)
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>)
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>)


Line 61: Line 64:
The parameter <math>z</math> is an empirical term that relates the rotational rate of particles at radial positions within the charge to the rotational rate of the mill, and is defined as:
The parameter <math>z</math> is an empirical term that relates the rotational rate of particles at radial positions within the charge to the rotational rate of the mill, and is defined as:


:<math>z = \left (  1 - J_{tr} \right )^{0.4532}</math>
:<math>z = \left (  1 - J_{{\rm t}r} \right )^{0.4532}</math>


where <math>J_{tr}</math> is the volume fraction mill filling at radial position <math>r</math>, i.e. the fraction of the total volume between the mill centre and shell radius that is filled with charge.
where <math>J_{{\rm t}r}</math> is the volume fraction mill filling at radial position <math>r</math>, i.e. the fraction of the total volume between the mill centre and shell radius that is filled with charge.


Shells located between the top of the lifters and outer mill shell are locked into place by the lifters, and rotate at the mill rotational speed without loss.
Shells located between the top of the lifters and outer mill shell are locked into place by the lifters, and rotate at the mill rotational speed without loss.
Line 100: Line 103:
For ball mills, the characteristic media size may be estimated by neglecting ore particles and assuming the ball size size distribution is in an equilibrium state (ball make-up rate = ball ejection rate), in which case:
For ball mills, the characteristic media size may be estimated by neglecting ore particles and assuming the ball size size distribution is in an equilibrium state (ball make-up rate = ball ejection rate), in which case:


:<math>\bar x = 0.5559 D_B</math>
:<math>\bar x = 0.5559 D_{\rm B}</math>


where <math>D_B</math> is the make-up ball diameter.
where <math>D_{\rm B}</math> is the make-up ball diameter.


Note that Morrell's ball size equilibrium assumptions are also consistent with the tumbling mill media string approach described [[Tumbling Mill (Media Strings)|here]].
Note that Morrell's ball size equilibrium assumptions are also consistent with the tumbling mill media string approach described [[Tumbling Mill (Media Strings)|here]].
Line 112: Line 115:
==== Toe and shoulder positions ====
==== Toe and shoulder positions ====


The position of the '''toe''' of a shell, <math>\theta_{Tr}</math> (rad), is defined as:  
The position of the '''toe''' of a shell, <math>\theta_{{\rm T}r}</math> (rad), is defined as:  


:<math>\theta_{Tr} = 2.5307 (1.2796 - J_{tr}) (1 - \rm e^{-9(\phi_c - \phi)}) + \frac{\pi}{2}</math>
:<math>\theta_{{\rm T}r} = 2.5307 (1.2796 - J_{{\rm t}r}) (1 - \rm e^{-9(\phi_{\rm c} - \phi)}) + \frac{\pi}{2}</math>


where <math>\phi</math> (frac) is the theoretical [[Tumbling Mill (Speed)|fraction critical speed]], and the fraction of critical speed at which centrifuging actually occurs, <math>\phi_c</math> (frac), is:
where <math>\phi</math> (frac) is the theoretical [[Tumbling Mill (Speed)|fraction critical speed]], and the fraction of critical speed at which centrifuging actually occurs, <math>\phi_{\rm c}</math> (frac), is:


:<math> \phi_c =
:<math> \phi_{\rm c} =
     \begin{cases}
     \begin{cases}
       \phi & \phi>0.35(3.364-J_{tr})\\
       \phi & \phi>0.35(3.364-J_{{\rm t}r})\\
       0.35(3.364-J_{tr})& \phi \leq 0.35(3.364-J_{tr})\\
       0.35(3.364-J_{{\rm t}r})& \phi \leq 0.35(3.364-J_{{\rm t}r})\\
     \end{cases}
     \end{cases}
</math>
</math>


The position of the '''shoulder''' of a shell, <math>\theta_{Sr}</math> (rad), is:  
The position of the '''shoulder''' of a shell, <math>\theta_{{\rm S}r}</math> (rad), is:  


:<math>\theta_{Sr} = \frac{\pi}{2} \big( (0.3386 + 0.1041 \phi) + (1.54 - 2.5673 \phi) J_{tr} \big) \left (\theta_{Tr} - \frac{\pi}{2} \right )</math>
:<math>\theta_{{\rm S}r} = \frac{\pi}{2} \big( (0.3386 + 0.1041 \phi) + (1.54 - 2.5673 \phi) J_{{\rm t}r} \big) \left (\theta_{{\rm T}r} - \frac{\pi}{2} \right )</math>


This implementation of the Discrete Shell model further adopts the Delboni (2002) approach for shells at radial positions between the mill outer shell and the top of installed lifters.{{Delboni_and_Morrell_(2002)}}
This implementation of the Discrete Shell model further adopts the Delboni (2002) approach for shells at radial positions between the mill outer shell and the top of installed lifters.{{Delboni_and_Morrell_(2002)}}
Line 139: Line 142:
==== Slurry pool position ====
==== Slurry pool position ====


The position of the '''slurry pool''' level, <math>\theta_{TO}</math> (rad), was assumed to be equal to the charge toe, <math>\theta_{T}</math>, for grate mills. For overflow mills, a value of 3.395 radians was calculated where the trunnion radius, <math>r_t</math>, is one quarter (0.25) of the mill radius, <math>r_m</math>.
The position of the '''slurry pool''' level, <math>\theta_{\rm TO}</math> (rad), was assumed to be equal to the charge toe, <math>\theta_{\rm T}</math>, for grate mills. For overflow mills, a value of 3.395 radians was calculated where the trunnion radius, <math>r_{\rm t}</math>, is one quarter (0.25) of the mill radius, <math>r_{\rm m}</math>.


This implementation of the Discrete Shell model improves estimation of the slurry pool position for overflow mills by adopting the approach described by Morrell (2016) and corrected by Shi (2016):{{Morrell_(2016)}}{{Shi_(2016)}}
This implementation of the Discrete Shell model improves estimation of the slurry pool position for overflow mills by adopting the approach described by Morrell (2016) and typographically corrected by Shi (2016):{{Morrell_(2016)}}{{Shi_(2016)}}


:<math>\theta_{TO} = \arcsin \left ( \frac{r_t - h}{r_m} \right )</math>
:<math>\theta_{\rm TO} = \arcsin \left ( \frac{r_{\rm t} - h}{r_{\rm m}} \right )</math>


where <math>h</math> is the height of slurry flow above the level of the trunnion lip:  
where <math>h</math> is the height of slurry flow above the level of the trunnion lip:  


:<math>h = \frac{1}{0.67} \left ( \frac{2Q}{\pi r_t g^{0.5}} \right )^{\frac{2}{3}}</math>
:<math>h = \frac{1}{0.67} \left ( \frac{2Q}{\pi r_{\rm t} g^{0.5}} \right )^{\frac{2}{3}}</math>


and <math>Q</math> is the volumetric flow rate of pulp to/from the overflow mill.
and <math>Q</math> is the volumetric flow rate of pulp to/from the overflow mill.
Line 159: Line 162:
where <math>\beta_r</math> is the fraction of total shell volume in the active portion. <math>\beta_r</math> is estimated as:
where <math>\beta_r</math> is the fraction of total shell volume in the active portion. <math>\beta_r</math> is estimated as:


:<math>\beta_r = \frac{t_{cr}}{t_{cr}+t_{fr}}</math>
:<math>\beta_r = \frac{t_{{\rm c}r}}{t_{{\rm c}r}+t_{{\rm f}r}}</math>


where <math>t_{cr}</math> is the time taken to travel between the toe and shoulder at radial position <math>r</math> within the active portion of the shell, and <math>t_{fr}</math> is the time taken to travel in free flight between the shoulder and toe at radial position <math>r</math>. i.e.,
where <math>t_{{\rm c}r}</math> is the time taken to travel between the toe and shoulder at radial position <math>r</math> within the active portion of the shell, and <math>t_{{\rm f}r}</math> is the time taken to travel in free flight between the shoulder and toe at radial position <math>r</math>. i.e.,


:<math>t_{cr} = \frac{2 \pi + \theta+{Sr} - \theta_{Tr}}{2 \pi N_r}</math>
:<math>t_{{\rm c}r} = \frac{2 \pi + \theta_{{\rm S}r} - \theta_{{\rm T}r}}{2 \pi N_r}</math>


:<math>t_{fr} = 2r \left( \frac{\sin \theta_{Sr} - \sin \theta_{Tr}}{g} \right )^{0.5}</math>
:<math>t_{{\rm f}r} = 2r \left( \frac{\sin \theta_{{\rm S}r} - \sin \theta_{{\rm T}r}}{g} \right )^{0.5}</math>


=== Charge density ===
=== Charge density ===
Line 172: Line 175:


This implementation adopts Morrell's 1996 approach to compute charge density, which includes a term for the fraction of void space occupied by slurry:{{Morrell_(1996a)}}
This implementation adopts Morrell's 1996 approach to compute charge density, which includes a term for the fraction of void space occupied by slurry:{{Morrell_(1996a)}}
:<math>\rho_c = \frac{J_t \rho_o (1 - E + EUS) + J_B( \rho_B - \rho_o)(1 - E) + J_tEU(1 - S)}{J_t}</math>
:<math>\rho_{\rm c} = \frac{J_{\rm t} \rho_{\rm o} (1 - E + EUS) + J_{\rm B}( \rho_{\rm B} - \rho_{\rm o})(1 - E) + J_{\rm t}EU(1 - S)}{J_{\rm t}}</math>


where:
where:
* <math>J_t</math> is the volumetric fraction of the mill occupied by balls and coarse rock (including void space and interstitial slurry) (v/v).
* <math>J_{\rm t}</math> is the volumetric fraction of the mill occupied by balls and coarse rock (including void space and interstitial slurry) (v/v).
* <math>\rho_o</math> is the density of ore (t/m<sup>3</sup>)
* <math>\rho_{\rm o}</math> is the density of ore (t/m<sup>3</sup>)
* <math>E</math> is volumetric fraction of interstitial void space in the charge, typically 0.4 (v/v)
* <math>E</math> is volumetric fraction of interstitial void space in the charge, typically 0.4 (v/v)
* <math>U</math> is the volumetric fraction of interstitial grinding media voidage occupied by slurry (v/v), <math>U \leq 1</math>
* <math>U</math> is the volumetric fraction of interstitial grinding media voidage occupied by slurry (v/v), <math>U \leq 1</math>
* <math>S</math> is the volume fraction of solids in the mill discharge (v/v)
* <math>S</math> is the volume fraction of solids in the mill discharge (v/v)
* <math>J_B</math> is the volumetric fraction of the mill occupied by balls (including voids) (v/v)
* <math>J_{\rm B}</math> is the volumetric fraction of the mill occupied by balls (including voids) (v/v)


=== Conical ends ===
=== Conical ends ===
Line 194: Line 197:
=== No-load power ===
=== No-load power ===


This implementation of the Discrete Shell model uses Morrell's 1996 term for no-load power:<ref name="Morrell_(1996a)" />
This implementation of the Discrete Shell model uses Morrell's 1996 term for no-load power:{{Morrell (1996a)}}


:<math>\text{No-load power} = 1.68D^{2.05} \left [\phi (0.667L_d+L \right ]^{0.82}</math>
:<math>\text{No-load power} = 1.68D^{2.05} \left [\phi (0.667L_{\rm d}+L \right ]^{0.82}</math>


where <math>D</math> is mill diameter inside liners (m) and <math>L_d</math> is length of the cone end (m).
where <math>D</math> is mill diameter inside liners (m) and <math>L_{\rm d}</math> is length of the cone end (m).


The length of the cone end, <math>L_d</math> (m), is:
The length of the cone end, <math>L_{\rm d}</math> (m), is:


:<math>L_d = (r_m - r_t) \tan \alpha_{c}</math>
:<math>L_{\rm d} = (r_{\rm m} - r_{\rm t}) \tan \alpha_{c}</math>


where <math>\alpha_{c}</math> is the cone angle, measured as the angular displacement of the cone surface from the vertical direction.
where <math>\alpha_{c}</math> is the cone angle, measured as the angular displacement of the cone surface from the vertical direction.
Line 210: Line 213:
The Morrell D model adopts the algorithm outlined below to compute total mill power draw:
The Morrell D model adopts the algorithm outlined below to compute total mill power draw:


# The charge is divided into a number of shells based on the total charge volume, <math>J_t</math>, the user-defined characteristic media size, <math>\bar x</math>, and an estimate of the charge inner surface radius, <math>r_i</math>
# The charge is divided into a number of shells based on the total charge volume, <math>J_{\rm t}</math>, the user-defined characteristic media size, <math>\bar x</math>, and an estimate of the charge inner surface radius, <math>r_i</math>
# The radial position, rotational speed, power draw and volume of each individual shell is then computed using the relations described in the previous sections.
# The radial position, rotational speed, power draw and volume of each individual shell is then computed using the relations described in the previous sections.
# The charge inner surface radius, and hence the number of shells, is re-estimated and the calculation steps 1 - 3 repeated until the sum of shell volumes matches the total charge volume.
# The charge inner surface radius, and hence the number of shells, is re-estimated and the calculation steps 1 - 3 repeated until the sum of shell volumes matches the total charge volume.
Line 218: Line 221:
# Total power draw is finally calculated by adding the net power and no-load power values.
# Total power draw is finally calculated by adding the net power and no-load power values.


== Additional notes ==
=== Additional notes ===


The Morrell D model requires an estimation of the charge particle size distribution (balls and coarse ore), and lifter geometry, both of which are typically not available during normal mill operation. In addition, the model applies a a multi-step, looping computational algorithm which makes it unsuited to spreadsheet-style calculations. For these reasons, the Morrell D model has not been tested and applied as extensively as the Morrell Continuum and Empirical models.
The Morrell D model requires an estimation of the charge particle size distribution (balls and coarse ore), and lifter geometry, both of which are typically not available during normal mill operation. In addition, the model applies a a multi-step, looping computational algorithm which makes it unsuited to spreadsheet-style calculations. For these reasons, the Morrell D model has not been tested and applied as extensively as the Morrell Continuum and Empirical models.


Nevertheless, the Morrell D model may find utility when coupled with process models that predict mill load and ball particle size distributions (e.g. [[AG/SAG Mill (Mutambo)]] and [[Tumbling Mill (Media Strings)]]), and lifter wear measurements from modern laser scanning devices.
Nevertheless, the Morrell D model may find utility when coupled with process models that predict mill load and ball particle size distributions (e.g. [[AG/SAG Mill (Variable Rates)]] and [[Tumbling Mill (Media Strings)]]), and lifter wear measurements from modern laser scanning devices.


Like the Continuum and Empirical models, the Morrell D model is only valid for grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>. The slurry pool present in overflow discharge mills is included within the model formulation via the <math>\theta_{TO}</math> term, as described above.
Like the Continuum and Empirical models, the Morrell D model is only valid for grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>. The slurry pool present in overflow discharge mills is included within the model formulation via the <math>\theta_{\rm TO}</math> term, as described above.
</hide>


== Excel ==
== Excel ==
Line 243: Line 247:
D\text{ (m)}\\
D\text{ (m)}\\
L\text{ (m)}\\
L\text{ (m)}\\
D_t\text{ (m)}\\
D_{\rm t}\text{ (m)}\\
\alpha_{c}\text{ (degrees)}\\
\alpha_{c}\text{ (degrees)}\\
h\text{ (m)}\\
h\text{ (m)}\\
\rho\text{ (rad)}\\
\rho\text{ (rad)}\\
\text{Mill speed (rpm)}\\
\text{Mill speed (rpm)}\\
J_t\text{ (v/v)}\\
J_{\rm t}\text{ (v/v)}\\
J_B\text{ (v/v)}\\
J_{\rm B}\text{ (v/v)}\\
U\text{ (v/v)}\\
U\text{ (v/v)}\\
\bar x\text{ (m)}\\
\bar x\text{ (m)}\\
\rho_o\text{ (t/m}^{\text{3}}\text{)}\\
\rho_{\rm o}\text{ (t/m}^{\text{3}}\text{)}\\
\rho_L\text{ (t/m}^{\text{3}}\text{)}\\
\rho_{\rm L}\text{ (t/m}^{\text{3}}\text{)}\\
\rho_B\text{ (t/m}^{\text{3}}\text{)}\\
\rho_{\rm B}\text{ (t/m}^{\text{3}}\text{)}\\
\text{Discharge pulp density (}\% \text{ w/w)}\\
\text{Discharge pulp density (}\% \text{ w/w)}\\
\text{Discharge mechanism}\\
\text{Discharge mechanism}\\
\gamma\\
\gamma\\
Q_v\text{ (m}^{\text{3}}\text{/h)}\\
Q_{\rm V}\text{ (m}^{\text{3}}\text{/h)}\\
\end{bmatrix},\;\;\;\;\;\;
\end{bmatrix},\;\;\;\;\;\;


Line 278: Line 282:


\begin{bmatrix}
\begin{bmatrix}
\theta_{S1} \text{ (rad)}\\
\theta_{\rm S1} \text{ (rad)}\\
\vdots\\
\vdots\\
\theta_{Sn} \text{ (rad)}
\theta_{{\rm S}n} \text{ (rad)}
\end{bmatrix}
\end{bmatrix}


\begin{bmatrix}
\begin{bmatrix}
\theta_{T1} \text{ (rad)}\\
\theta_{\rm T1} \text{ (rad)}\\
\vdots\\
\vdots\\
\theta_{Tn} \text{ (rad)}
\theta_{{\rm T}n} \text{ (rad)}
\end{bmatrix}
\end{bmatrix}


Line 300: Line 304:


where:
where:
* <math>D_t</math> is the diameter of the discharge trunnion (m), i.e. <math>D_t = 2 r_t</math>
* <math>D_{\rm t}</math> is the diameter of the discharge trunnion (m), i.e. <math>D_{\rm t} = 2 r_{\rm t}</math>
* <math>h</math> is the lifter height (m)
* <math>h</math> is the lifter height (m)
* <math>\rho</math> is the lifter face angle (deg.)
* <math>\rho</math> is the lifter face angle (deg.)
* <math>\text{Mill speed}</math> is the rotational speed of the mill (rpm)
* <math>\text{Mill speed}</math> is the rotational speed of the mill (rpm)
* <math>\rho_L</math> is the density of liquids (t/m<sup>3</sup>)
* <math>\rho_{\rm L}</math> is the density of liquids (t/m<sup>3</sup>)
* <math>\text{Discharge pulp density}</math> is the mass fraction of solids in the discharge pulp (% w/w)
* <math>\text{Discharge pulp density}</math> is the mass fraction of solids in the discharge pulp (% w/w)
* <math>\text{Discharge mechanism}</math> is the discharge configuration type, ''0 = Grate, 1 = Overflow''
* <math>\text{Discharge mechanism}</math> is the discharge configuration type, ''0 = Grate, 1 = Overflow''
* <math>Q_v</math> is the volumetric discharge flow rate of pulp from the mill (m<sup>3</sup>/h)
* <math>Q_{\rm V}</math> is the volumetric discharge flow rate of pulp from the mill (m<sup>3</sup>/h)
* <math>\text{Net impact power}</math> is the power draw attributable to the impact mechanism (kW)
* <math>\text{Net impact power}</math> is the power draw attributable to the impact mechanism (kW)
* <math>\text{Net att/abr power}</math> is the power draw attributable to the attrition/abrasion mechanisms (kW)
* <math>\text{Net att/abr power}</math> is the power draw attributable to the attrition/abrasion mechanisms (kW)
* <math>n</math> is the number of discrete shells
* <math>n</math> is the number of discrete shells
* <math>r_i</math> is the radius of shell <math>i</math> (m)
* <math>r_i</math> is the radius of shell <math>i</math> (m)
* <math>\theta_{Si}</math> is the angular position of the shoulder of shell <math>i</math> (rad)
* <math>\theta_{{\rm S}i}</math> is the angular position of the shoulder of shell <math>i</math> (rad)
* <math>\theta_{Ti}</math> is the angular position of the toe of shell <math>i</math> (rad)
* <math>\theta_{{\rm T}i}</math> is the angular position of the toe of shell <math>i</math> (rad)
* <math>P_i</math> is the power drawn by shell <math>i</math> (kW)
* <math>P_i</math> is the power drawn by shell <math>i</math> (kW)


Line 323: Line 327:
The Morrell Discrete Shell power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.
The Morrell Discrete Shell power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.


{{SysCAD_Table_Header}}
{{SysCAD (Text, Table Header)}}
 
|-
|-
! colspan="3" style="text-align:left;" |''MorrellC''
! colspan="3" style="text-align:left;" |''MorrellC''
{{SysCAD (Text, Help Link)}}
|-
|-
|MillDiameter
|MillDiameter
Line 414: Line 422:
|style="background: #eaecf0" | Display
|style="background: #eaecf0" | Display
|Net power attributable to attrition/abrasion
|Net power attributable to attrition/abrasion
|-
|NetPower
|style="background: #eaecf0" | Display
|Charge motion power.
|-
|-
|GrossPower
|GrossPower

Latest revision as of 11:15, 4 December 2024

Description

This article describes the Morrell Discrete Shell (Morrell D) method for estimating the power draw of a tumbling mill.[1] The Morrel D model adopts a more sophisticated treatment of charge dynamics than the Morrell Continuum method:

  • The total charge is subdivided into discrete layers, or shells, whose size and position may individually vary due to grinding media size, mill speed, lift bar geometry and other conditions.
  • The rate at which potential and kinetic energy is imparted to each shell during mill rotation is calculated separately and subsequently summed to estimate the total mill power draw.

Model theory

Nuvola apps important blue.svg.png This content is available to registered users. Please log in to view.

Excel

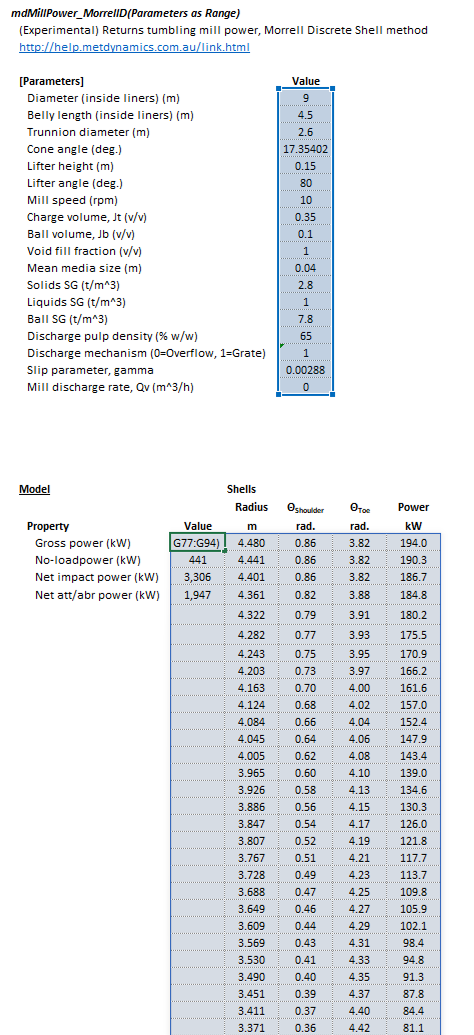
The Morrell Discrete Shell mill power model may be invoked from the Excel formula bar with the following function call: 

=mdMillPower_MorrellD(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:


where:

  • is the diameter of the discharge trunnion (m), i.e.
  • is the lifter height (m)
  • is the lifter face angle (deg.)
  • is the rotational speed of the mill (rpm)
  • is the density of liquids (t/m3)
  • is the mass fraction of solids in the discharge pulp (% w/w)
  • is the discharge configuration type, 0 = Grate, 1 = Overflow
  • is the volumetric discharge flow rate of pulp from the mill (m3/h)
  • is the power draw attributable to the impact mechanism (kW)
  • is the power draw attributable to the attrition/abrasion mechanisms (kW)
  • is the number of discrete shells
  • is the radius of shell (m)
  • is the angular position of the shoulder of shell (rad)
  • is the angular position of the toe of shell (rad)
  • is the power drawn by shell (kW)
Figure 4. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Morrell Discrete Shell power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
MorrellC
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
MillDiameter Input/Display Diameter of the mill (inside liners).
BellyLength Input/Display Length of the cylindrical section (belly) of the mill (inside liners).
TrunnionDiameter Input/Display Diameter of the trunnion (inside liners).
ConeAngle Input/Display Angular displacement of the cone surface from the vertical direction.
LifterHeight Input Height of the lifters above the liner surface
LifterAngle Input Angle between the face and the base of the lifter
MillRPM Input/Display Mill rotational speed
Jt Input/Display Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
BallLoadVol Input/Display Volumetric fraction of the mill occupied by balls (including voids).
VoidFillFraction Input/Display Volumetric fraction of interstitial grinding media voidage occupied by slurry.
MeanMediaSize Input Characteristic media size,
SolidsSG Display Specific Gravity or density of solids.
LiquidsSG Display Specific Gravity or density of liquids.
BallSG Input/Display Specific Gravity or density of balls.
Cw Display Mass fraction of solids in discharge slurry.
DischargeType Grate/Overflow Discharge configuration, grate or overflow.
Gamma Input Value of the slip coefficient,
ThetaShoulder Display Angle of the shoulder of the outermost charge shell.
ThetaToe Display Angle of the toe of the outermost charge toe
NoLoadPower Display Power input to the motor when the mill is empty (no balls, rocks or slurry).
NetImpactPower Display Net power attributable to impact
NetAttAbrPower Display Net power attributable to attrition/abrasion
NetPower Display Charge motion power.
GrossPower Display Power input to the motor.

See also

References

  1. ↑ Morrell, S., 1993. The prediction of power draw in wet tumbling mills (Doctoral dissertation, University of Queensland).
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=Tumbling_Mill_(Power,_Morrell_Discrete_Shell)&oldid=2209"