Tumbling Mill (Power, Hilden and Powell): Difference between revisions
Scott Munro (talk | contribs) m (1 revision imported) |
imported>Scott.Munro mNo edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 11: | Line 11: | ||
== Model theory == | == Model theory == | ||
{{Restricted content}} | |||
<hide> | |||
Hilden and Powell's approach adopts Morrell's (1996) expression for tumbling mill power draw:{{Morrell (1996a)}} | Hilden and Powell's approach adopts Morrell's (1996) expression for tumbling mill power draw:{{Morrell (1996a)}} | ||
| Line 186: | Line 189: | ||
:<math>A_{\rm Sect} = \frac{(\theta_{\rm T} - \theta_{\rm L}}{2} . (R^2 - r_{\rm i}^2)</math> | :<math>A_{\rm Sect} = \frac{(\theta_{\rm T} - \theta_{\rm L}}{2} . (R^2 - r_{\rm i}^2)</math> | ||
The slurry toe parameter <math>\theta_{\rm L}</math> cannot be algebraically isolated in the above equations. Therefore, an iterative numerical method is used to solve the value of <math>\theta_{\rm L}</math> that yields the required value of <math>A_x</math> | The slurry toe parameter <math>\theta_{\rm L}</math> cannot be algebraically isolated in the above equations. Therefore, an iterative numerical method is used to solve the value of <math>\theta_{\rm L}</math> that yields the required value of <math>A_x</math>. | ||
=== Charge density === | === Charge density === | ||
| Line 258: | Line 261: | ||
| 6.1 | | 6.1 | ||
|} | |} | ||
</hide> | |||
== Excel == | == Excel == | ||
Latest revision as of 11:16, 4 December 2024
Description
This article describes the Hilden and Powell (2018) approach for estimating the power draw of a tumbling mill.[1]
Hilden and Powell extended Morrell's (1996, 2016) approaches to include the following features:[2][3]
- Partial filling of the charge void space with slurry in two directions, from the charge shoulder towards the toe and from the outer shell towards the mill centre
- Estimation of the fraction of a slurry pool which settles across the centre of the mill profile and thus does not contribute to power draw
- No-load power based on mill drive type and size
Model theory
Excel
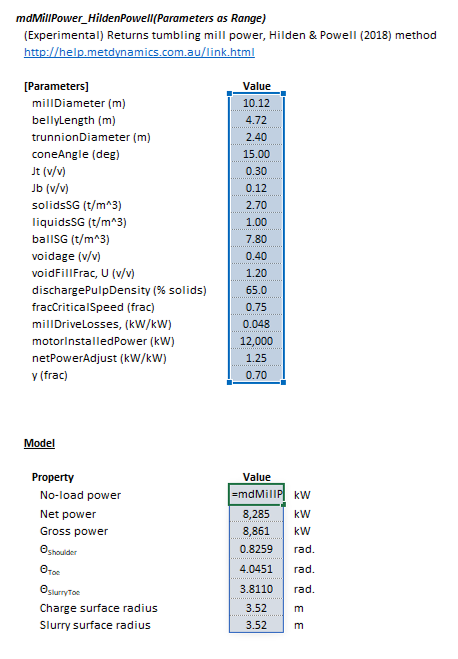
The Hilden and Powell mill power model may be invoked from the Excel formula bar with the following function call:
=mdMillPower_HildenPowell(Parameters as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:
|
|
SysCAD
The Hilden and Powell power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.
| Tag (Long/Short) | Input / Display | Description/Calculated Variables/Options |
|---|---|---|
| HildenPowell | ||
| HelpLink | Opens a link to this page using the system default web browser. Note: Internet access is required. | |
| MillDiameter | Display | Diameter of the mill (inside liners). |
| BellyLength | Display | Length of the cylindrical section (belly) of the mill (inside liners). |
| TrunnionDiameter | Display | Diameter of the trunnion (inside liners). |
| ConeAngle | Display | Angular displacement of the cone surface from the vertical direction. |
| Jt | Display | Volumetric fraction of the mill occupied by balls and coarse rock (including voids). |
| BallLoadVol | Display | Volumetric fraction of the mill occupied by balls (including voids). |
| SolidsSG | Display | Specific Gravity or density of solids. |
| BallSG | Display | Specific Gravity or density of balls. |
| LiquidsSG | Display | Specific Gravity or density of liquids. |
| Voidage | Input/Display | Volumetric fraction of interstitial void space in the charge. Usually 0.4. Note: The Dynamic Perfect Mixing ball mill model uses Shi's dynamic charge porosity estimation to align power draw predictions with the adopted slurry filling approach. |
| U | Display | Volumetric fraction of interstitial grinding media voidage occupied by slurry. |
| Cw | Display | Mass fraction of solids in discharge slurry. |
| FracCS | Display | Fraction critical speed of the mill. |
| MillDriveLosses | Input | Mill drive motor power loss factor. |
| MotorInstalledPower | Input | Maximum power draw of installed mill motor. |
| NetPowerAdjust | Input | Lumped calibration parameter accounting for power losses. Found to be a value of 1.26 for industrial mills. |
| y | Input | Profile shape factor. |
| ThetaShoulder | Display | Angle of the charge shoulder. |
| ThetaToe | Display | Angle of the charge toe. |
| ThetaSlurryToe | Display | Angle of the toes of the slurry component |
| ChargeSurfaceRadius | Display | Radius of the inner surface of the charge. |
| SlurrySurfaceRadius | Display | Radius of the inner surface of the slurry component. |
| NoLoadPower | Display | Power input to the motor when the mill is empty (no balls, rocks or slurry). |
| NetPower | Display | Charge motion power, including losses. |
| GrossPower | Display | Power input to the motor. |
See also
References
- ↑ Hilden, M.M. and Powell, M.S., 2018. A model of SAG mill power incorporating slurry filling and its application to real-time mill performance analysis. Paper presented at Comminution '18, Cape Town, South Africa, April 16-19, 2018.
- ↑ Morrell, S., 1996. Power draw of wet tumbling mills and its relationship to charge dynamics. Pt. 1: a continuum approach to mathematical modelling of mill power draw. Transactions of the Institution of Mining and Metallurgy. Section C. Mineral Processing and Extractive Metallurgy, 105.
- ↑ Morrell, S., 2016. Modelling the influence on power draw of the slurry phase in Autogenous (AG), Semi-autogenous (SAG) and ball mills. Minerals Engineering, 89, pp.148-156.