HPGR (Torres): Difference between revisions

From Met Dynamics
Jump to navigation Jump to search
imported>Scott.Munro
imported>Scott.Munro
Line 4: Line 4:


== Model theory ==
== Model theory ==
<!--
[[File:HPGRTorres5.png|thumb|400px|Figure 1. Schematic diagram of an HPGR showing principal dimensions (after Torres and Casali, 2009).{{Torres and Casali (2009)}}]]


[[File:HPGRTorres6.png|thumb|500px|Figure 2. Schematic diagram illustrating the single particle and particle bed compression zones of an HPGR (after Torres and Casali, 2009).{{Torres and Casali (2009)}}]]
-->
{{Under construction|section}}
{{Under construction|section}}
<!-- SME handbook has a reference to cake density factor being 80-85% -->
<!--
Torres and Casali (2009) proposed a phenomenological HPGR model that combines equipment specifications, operating variables and ore characteristics to predict throughput, power draw, and size reduction performance.{{Torres and Casali (2009)}}
 
Figure 1 presents the principal dimensions of an HPGR machine, which are relevant to throughput and power draw behaviour.
 
Torres and Casali suggest that particles traversing the space between the two counter-rotating rolls of an HPPR are subject to two modes of particle breakage:
# ''Single particle compression'', where individual particles are nipped and crushed between the rolls in isolation from neighbouring particles.
# ''Particle bed compression'', where particles are packed into in close contact with their neighbours and break as the ensemble is drawn into the rolls and stressed.
 
Figure 2 illustrates the arrangement of the single particle and particle bed compression zones in relation to HPGR geometry.
 
The throughput, power draw, and size reduction sub-models are described in detail below.
 
=== Throughput ===
 
The solids mass throughput flow rate, <math>G_{\rm s}</math> (t/h), of an HPGR may be estimated as:
 
:<math>G_{\rm s} = 3600 \cdot \delta s_0 L U</math>
 
where:
* <math>\delta</math> is the bulk density of discharge cake solids (t/m<sup>3</sup>)
* <math>s_0</math> is the operating gap (m)
* <math>L</math> is the length of the rolls (m)
* <math>U</math> is the peripheral rolls velocity (m/s)
 
Similarly, the peripheral rolls velocity (<math>U</math>) for a given solids mass throughput flow rate (<math>G_{\rm s}</math>) is:
 
:<math>U = \dfrac{G_{\rm s}}{3600 \cdot \delta s_0 L}</math>
 
The bulk density of the discharge cake solids (<math>\delta</math>) can be specified in terms of the solid material density, <math>\rho_{\rm S}</math> (t/m<sup>3</sup>), by:
 
:<math>\delta = C_{\rho} \rho_{\rm S}</math>
 
where <math>C_{\rho}</math> is the ''cake density factor'' (frac). A cake density factor (<math>C_{\rho}</math>) of 0.80 - 0.85 may be typical for operating HPGR machines.{{Dunne et al. (2019)}}
 
=== Power ===
 
The compression force, <math>F</math> (kN), applied to the material in the bed compression zone due to the operating pressure of the rolls, <math>R_{\rm p}</math> (bar), is:
 
:<math>F = 100 R_{\rm p} \dfrac{D}{2} L</math>
 
The start of the bed compression zone is defined by the size of the interparticle compression angle, <math>\alpha_{\rm IP}</math> (rad), which is:
 
:<math>\alpha_{\rm IP} = \arccos \left ( \dfrac{1}{2D} \left [ (s_0 + D) + \sqrt{(s_0 + D)^2 - \dfrac{4 s_0 \delta D}{\rho_{\rm a}}} \phantom{1} \right ] \right )</math>
 
where <math>D</math> is the diameter of the rolls (m).
 
The compression force exerts a torque on each roll, which results in the following expression for power draw:
 
:<math>P = 2 \sin \left ( C_{\rm IP} . \alpha_{\rm IP} \right)U</math>
 
where <math>C_{\rm IP}</math> is the fraction of the interparticle compression angle at which the compression force acts. Torres and Casali suggest a value of <math>C_{\rm IP} = 0.5</math>. This implementation allows a user-specified value of <math>C_{\rm IP}</math>, so that the power draw of a simulated machine may be matched to the measured power draw of an operating machine.
 
Finally, the specific energy consumption, <math>W</math> (kWh/t), is:
 
:<math>W = \dfrac{P}{G_{\rm s}}</math>
 
=== Breakage ===
 
[[File:HPGRTorres7.png|thumb|325px|Figure 3. Process flowchart outlining the progression of HPGR feed though single particle compression and particle bed compression zones to the edge, centre and total products (after Torres and Casali, 2009).{{Torres and Casali (2009)}}]]
 
Insert single/interparticle flow chart here.
 
==== Single particle compression ====
 
Modified to account for material mid-interval xc.
 
:<math>x_{\rm c} = s_0 + D(1 - \cos \alpha_{\rm IP})</math>
 
:<math>p_i^{\rm SP} = \sum_{j=1}^{i} b_{ij} f_j^{\rm SP}</math>
 
:<math>
f_i^{\rm SP} =
\begin{cases}
(Q_{M,F})_i & d_i \geq x_{\rm c}\\
(Q_{M,F})_i \left ( \frac{d_{i-1} - x_{\rm c}}{d_{i-1} - d_i} \right ) & d_{i-1} > x_{\rm c} \geq d_i\\
0 & d_{i-1} < x_{\rm c}
\end{cases}
</math>
 
where:
* <math>Q_{\rm M,F}</math> is feed solids mass flow rate by size and ore type (t/h)
* <math>d_i</math> is the size of the square mesh interval that mass is retained on (mm)
* <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm)
 
==== Interparticle compression ====
 
Discuss discretisation into NB blocks.
* <math>N_{\rm B}</math> is the number of model blocks
 
Show differential equation here?
 
Then solution to plug flow (batch) grinding equation.
 
:<math>p_{i,k} = \sum_{j=1}^{i}A_{ij,k} \exp \left( - \dfrac{S_{j,k}}{v_z} z^* \right )</math>
 
where:
* dsfdsf
 
and z* is height of particle compression zone:
 
:<math>z^* = \dfrac{D}{2} \sin \alpha_{\rm IP}</math>
 
A is defined as:
 
:<math>
A{_ij,k} =
\begin{cases}
0 & i<j\\
\sum\limits_{l=1}^{i-1} \dfrac{b_{il} S_{l,k}}{S_{i,k} - S_{j,k} A_{lj,k}} & i>j\\
f_i^{\rm IP} - \sum\limits_{l=1}^{i-1} A_{il,k} & i=j\\
\end{cases}
</math>
 
:<math>S_{i,j} = \dfrac{P_k}{H_k} S_i^E</math>
 
:<math>H_k = \dfrac{1}{N_{\rm B}} G_{\rm s} \dfrac{z^*}{3600 \cdot U}</math>
 
Need to make note that z* and U in Hk cancel out z* and vz in plug flow grinding equation, so end up with Gs / Nb.
 
The energy-specific selection function associated with the Herbst and Fuerstenau model is:{{King (2012)}}
 
:<math>S^{\rm E}_i = S^{\rm E}_1 \exp \left ( \zeta_1 \ln{ \left ( \dfrac{\bar d_{i}}{d_{{\rm p}1}} \right )} + \zeta_2 \left [ \ln{ \left ( \dfrac{\bar d_{i}}{d_{{\rm p}1}} \right )} \right ] ^2  \right )</math>
 
where:
* <math>S^{\rm E}_1</math> is the value of the energy-specific selection function (<math>S^{\rm E}_i</math>) at a nominal reference particle size <math>\bar d_{{\rm p}1}</math> (mm)
* <math>\bar d_{i}</math> is the [[Conversions|geometric mean size]] of particles in size interval <math>i</math> (mm)
* <math>\zeta_1</math> and <math>\zeta_2</math> are coefficients that characterise the shape of the energy-specific selection function curve
 
The Austin and Luckie (1972) equation for the non-normalised cumulative breakage function is:{{Austin and Luckie (1972)}}{{Sepulveda (2005)}}
 
:<math>B_{ij} = \beta_{0j} \left ( \dfrac{d_i}{d_{j+1}} \right )^{\beta_1} + (1 - \beta_{0j}) \left ( \dfrac{d_i}{d_{j+1}} \right )^{\beta_2}</math>
 
where:
 
:<math>\beta_{0j}= \beta_{0} {\bar d_i}^{- \beta_{01}}</math>
 
and:
* <math>B_{ij}</math> is the cumulative breakage function, i.e. <math>b_{ij} = B_{ij} - B_{i+1,j}</math>
* <math>\beta_0</math>, <math>\beta_1</math>, <math>\beta_2</math>, <math>\beta_{0j}</math> and <math>\beta_{01}</math> are coefficients that determine the shape of the cumulative breakage function curve
 
The Austin and Luckie equation reduces to a normalised breakage function when <math>\beta_{01}</math> is set to zero.
 
Then, per block power is:
 
:<math>P_k = 2 F \sin \left ( \dfrac{\alpha_{\rm IP}}{2} \right ) U \left [ \frac{(L^2 - 4 {y_k}^2)}{\sum_{j=1}^{N_{\rm B}} (L^2 - 4 {y_j}^2)} \right ]</math>
 
where <math>y</math> is the block position (m):
 
:<math>y_k = \dfrac{L}{2 N_{\rm B}} (2k - N_{\rm B} - 1)</math>
 
Note: May need to change these equations from wt % to t/h pi. e.g. no 1/NB factors.
 
Then total product from HPGR is:
:<math>p_i^{\rm HPGR} = \dfrac{1}{N_{\rm B}} \sum_{k=1}^{N_{\rm B}} p_{i,k}</math>
 
Edge and centre products are calculated from:
 
:<math>E = 0.5 a N_{\rm B}</math>
 
where <math>a</math> is the edge fraction (frac).
 
:<math>p_i^{\rm E} = \dfrac{1}{E} \left [ \sum_{k=1}^{\lfloor E \rfloor} p_{i,k} + (E - \lfloor E \rfloor) p_{i, \lceil E \rceil} \right ]</math>
 
Linear interpolation in the above (?)
 
:<math>p_i^{\rm C} = \dfrac{1}{1-a} \left (p_i^{\rm HPGR} - ap_i^E \right )</math>
 
==== Herbst-Fuerstenau grinding model ====
 
The specific energy plug flow grinding formulation presented by Torres and Casali is equivalent (subset?) to the Herbst-Fuerstenau formulation.
 
HF model used in this implementation of Torres and Casali model. i.e. Each block is a single instance of an HF model. Therefore parameters from T&C model implementations (or paper) will not work, need to be refitted.
 
:''Main article'': [[Mill (Herbst-Fuerstenau)]]
 
==== Specific throughput ====
 
The specific throughput of an HPGR, <math>\dot m</math> (t.s/h.m<sup>3</sup>), is defined as:{{Kawatra (2006)}}
 
:<math>\dot m = \dfrac{G_{\rm s}}{DLU}</math>
-->


== Excel ==
== Excel ==
Line 24: Line 209:
D\text{ (m)}\\
D\text{ (m)}\\
L\text{ (m)}\\
L\text{ (m)}\\
s_0\text{ (m)}\\
R_{\rm p}\text{  (bar)}\\
R_{\rm p}\text{  (bar)}\\
\rho_{\rm a}\text{ (t/m}^3\text{)}\\
\rho_{\rm a}\text{ (t/m}^3\text{)}\\
Line 90: Line 276:


where:
where:
* <math>D</math> is the diameter of the rolls (m)
* <math>L</math> is the length of the rolls (m)
* <math>R_{\rm p}</math> is the operating pressure of the rolls (bar)
* <math>\rho_{\rm a}</math> is the bulk density of the feed solids (t/m<sup>3</sup>)
* <math>\text{Cake density factor}</math> is the ratio of cake bulk density to solids phase density (frac)
* <math>a</math> is the edge fraction (frac)
* <math>FracIP</math> is the fraction of the interparticle compression angle applied to compute power draw (deg/deg)
* <math>N_{\rm B}</math> is the number of model blocks
* <math>n</math> is the number of size intervals
* <math>n</math> is the number of size intervals
* <math>m</math> is the number of ore types
* <math>m</math> is the number of ore types
* <math>d_i</math> is the size of the square mesh interval that mass is retained on (mm)
* <math>d_{i+1}<d_i<d_{i-1}</math>, i.e. descending size order from top size (<math>d_{1}</math>) to sub mesh (<math>d_{n}=0</math> mm)
* <math>Q_{\rm M,F}</math> is feed solids mass flow rate by size and ore type (t/h)
* <math>\rho_{\rm S}</math> is the solid density (t/m<sup>3</sup>)
* <math>S^{\rm E}_1</math> is the value of the energy-specific selection function (<math>S^{\rm E}_i</math>) at a nominal reference particle size <math>\bar d_{{\rm p}1}</math> (mm)
* <math>\zeta_1</math> and <math>\zeta_2</math> are coefficients that characterise the shape of the energy-specific selection function curve
* <math>\beta_0</math>, <math>\beta_1</math>, <math>\beta_2</math>, and <math>\beta_{02}</math> are coefficients that determine the shape of the cumulative breakage function curve


=== Results ===
=== Results ===
Line 231: Line 402:


where:
where:
* <math>\delta</math> is the bulk density of discharge cake solids (t/m<sup>3</sup>)
* <math>x_{\rm c}</math> is the critical gap (m)
* <math>\alpha_{\rm IP}</math> is the interparticle compression angle (deg.)
* <math>G_{\rm s}</math> is the throughput (t/h)
* <math>U</math> is the circumferential rolls speed (m/s)
* <math>\text{Rolls rotational speed}</math> is the rotational speed of the rolls (rpm)
* <math>\text{Rolls rotational speed}</math> is the rotational speed of the rolls (rpm)
* <math>\dot m</math> is the specific throughput (t.s/m<sup>3</sup>.h)
* <math>\dot m</math> is the specific throughput (t.s/m<sup>3</sup>.h)
* <math>F</math> is the compression force (kN)
* <math>W</math> is the specific comminution energy (kWh/t)
* <math>P</math> is power draw (kW)
* <math>Q_{\rm M,P}</math> is the mass flow rate of particles in the overall, combined product (t/h)
* <math>Q_{\rm M,P}</math> is the mass flow rate of particles in the overall, combined product (t/h)
* <math>Q_{\rm M,E}</math> is the mass flow rate of particles in the ''edge'' product (t/h)
* <math>Q_{\rm M,E}</math> is the mass flow rate of particles in the ''edge'' product (t/h)
* <math>Q_{\rm M,C}</math> is the mass flow rate of particles in the ''centre'' product (t/h)
* <math>Q_{\rm M,C}</math> is the mass flow rate of particles in the ''centre'' product (t/h)
* <math>\bar d_{i}</math> is the [[Conversions|geometric mean size]] of particles in size interval <math>i</math> (mm)
* <math>S^{\rm E}</math> is the energy-specific selection function
* <math>B</math> is the cumulative breakage function (frac)
* <math>y</math> is block position (m)


=== Example ===
=== Example ===
Line 255: Line 414:
{|
{|
|- style="vertical-align:top;"
|- style="vertical-align:top;"
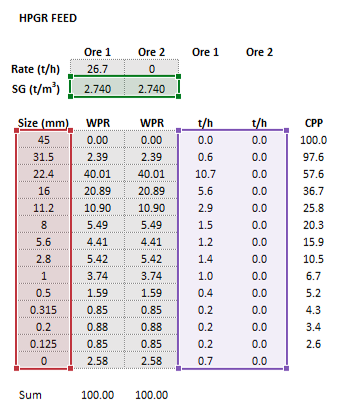
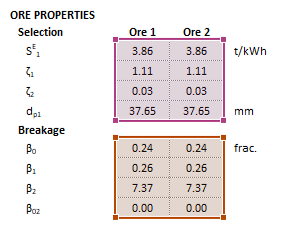
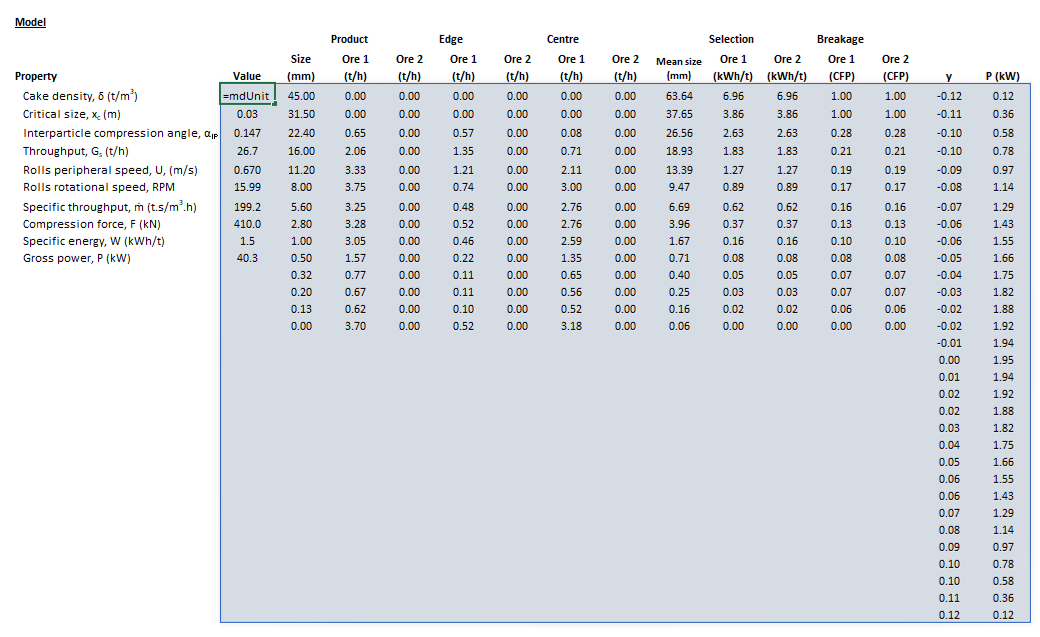
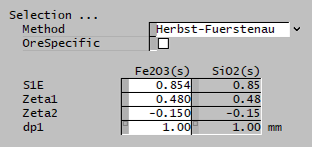
| [[File:HPGRTorres1.png|left|frame|Figure 1. Example showing the selection of the '''Parameters''' (blue frame) array in Excel.]]|| [[File:HPGRTorres2.png|left|frame|Figure 2. Example showing the selection of the '''Size''' (red frame), '''HPGRFeed''' (purple frame) and '''OreSG''' (green frame) arrays in Excel.]] || [[File:HPGRTorres3.png|left|frame|Figure 3. Example showing the selection of the '''Selection''' (pink frame) and '''Breakage''' (brown frame) arrays in Excel.]]  
| [[File:HPGRTorres1.png|left|frame|Figure 4. Example showing the selection of the '''Parameters''' (blue frame) array in Excel.]]|| [[File:HPGRTorres2.png|left|frame|Figure 5. Example showing the selection of the '''Size''' (red frame), '''HPGRFeed''' (purple frame) and '''OreSG''' (green frame) arrays in Excel.]] || [[File:HPGRTorres3.png|left|frame|Figure 6. Example showing the selection of the '''Selection''' (pink frame) and '''Breakage''' (brown frame) arrays in Excel.]]  
|-  
|-  
|colspan="3"| [[File:HPGRTorres4.png|left|frame|Figure 4. Example showing the outline of the '''Results''' (light blue frame) array in Excel.]]
|colspan="3"| [[File:HPGRTorres4.png|left|frame|Figure 7. Example showing the outline of the '''Results''' (light blue frame) array in Excel.]]
|}
|}


Line 279: Line 438:


{{SysCAD (Text, HPGR, No PSD Splits)}}
{{SysCAD (Text, HPGR, No PSD Splits)}}
== See also ==
* [[HPGR (Morrell-Tondo-Shi)|Morrell-Tondo-Shi HPGR model]]
* [[HPGR (Campos)|Campos HPGR model]]
* [[Mill (Herbst-Fuerstenau)| Herbst-Fuerstenau mill model]]


== References ==
== References ==

Revision as of 05:22, 30 September 2023

Description

This article describes the Torres and Casali (2009) model for comminution by High Pressure Grinding Rolls (HPGR).[1]

Model theory

Under construction icon-blue.svg.png This section is currently under construction. Please check back later for updates and revisions.

Excel

The Torres HPGR model may be invoked from the Excel formula bar with the following function call: 

=mdUnit_HPGR_Torres(Parameters as Range, Size as Range, HPGRFeed as Range, OreSG as Range, Selection as Range, Breakage as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

Inputs

The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row () x column () format:



where:

  • is the number of size intervals
  • is the number of ore types

Results

The results are displayed in Excel as an array corresponding to the matrix notation below:

where:

  • is the rotational speed of the rolls (rpm)
  • is the specific throughput (t.s/m3.h)
  • is the mass flow rate of particles in the overall, combined product (t/h)
  • is the mass flow rate of particles in the edge product (t/h)
  • is the mass flow rate of particles in the centre product (t/h)

Example

The images below show the selection of input arrays and output results in the Excel interface.

Figure 4. Example showing the selection of the Parameters (blue frame) array in Excel.
Figure 5. Example showing the selection of the Size (red frame), HPGRFeed (purple frame) and OreSG (green frame) arrays in Excel.
Figure 6. Example showing the selection of the Selection (pink frame) and Breakage (brown frame) arrays in Excel.
Figure 7. Example showing the outline of the Results (light blue frame) array in Excel.

SysCAD

The sections and variable names used in the SysCAD interface are described in detail in the following tables.

MD_HPGR page

The first tab page in the access window will have this name.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Tag Display This name tag may be modified with the change tag option.
Condition Display OK if no errors/warnings, otherwise lists errors/warnings.
ConditionCount Display The current number of errors/warnings. If condition is OK, returns 0.
GeneralDescription / GenDesc Display This is an automatically generated description for the unit. If the user has entered text in the 'EqpDesc' field on the Info tab (see below), this will be displayed here.

If this field is blank, then SysCAD will display the unit class ID.

Requirements
On CheckBox This enables the unit. If this box is not checked, then the material will pass straight through the crusher with no change to the size distribution.
Method Fixed Discharge The discharge particle size distribution is user defined. Different distributions can be used for different solids.
Morrell-Shi-Tondo The throughput, power draw and product size distribution are determined by the Morrell-Tondo-Shi model. Different parameters can be used for different solids.
Torres The throughput, power draw and product size distribution are determined by the Torres model. Different parameters can be used for different solids.
Campos The throughput, power draw and product size distribution are determined by the Campos model. Different parameters can be used for different solids.
Options
ShowQFeed CheckBox QFeed and associated tab pages (eg Sp) will become visible, showing the properties of the combined feed stream.
ShowQProd CheckBox QProd and associated tab pages (eg Sp) will become visible, showing the properties of the products.
SizeForPassingFracCalc Input Size fraction for % Passing calculation. The size fraction input here will be shown in the Stream Summary section.
FracForPassingSizeCalc Input Fraction passing for Size calculation. The fraction input here will be shown in the Stream Summary section.
Stream Summary
MassFlow / Qm Display The total mass flow in each stream.
SolidMassFlow / SQm Display The Solids mass flow in each stream.
LiquidMassFlow / LQm Display The Liquid mass flow in each stream.
VolFlow / Qv Display The total Volume flow in each stream.
Temperature / T Display The Temperature of each stream.
Density / Rho Display The Density of each stream.
SolidFrac / Sf Display The Solid Fraction in each stream.
LiquidFrac / Lf Display The Liquid Fraction in each stream.
Passing Display The mass fraction passing the user-specified size (in the field SizeForPassingFracCalc) in each stream.
Passes Display The user-specified (in the field FracForPassesSizeCalc) fraction of material in each stream will pass this size fraction.

HPGR page

The HPGR page is used to specify the input parameters for the HPGR model.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
HerbstFuerstenau
HelpLink ButtonModelHelp.png Opens a link to this page using the system default web browser. Note: Internet access is required.
Requirements
NumParallelUnits Input The number of parallel, identical units to simulate:
  • Feed is divided by the number of parallel units before being sent to the unit model.
  • Unit model product is multiplied back by the same value and returned to the SysCAD product stream.
  • All unit model result values are shown per parallel unit.
Parameters
RollDiameter / D Input Diameter of the rolls.
RollLength / L Input Length of the rolls.
OperatingPressure / Rp Input Operating pressure of the rolls.
FeedBulkDensity / Rhoa Input Bulk density of solids in the feed.
CakeDensityFactor Input Cake density factor.
EdgeFraction / a Input Fraction of the product collected from the edge of the rolls length, appearing in the edge product stream.
NumBlocks / Nb Input Number of model blocks, i.e. instances of the Herbst-Fuerstenau mill model along the length of the rolls.
Selection
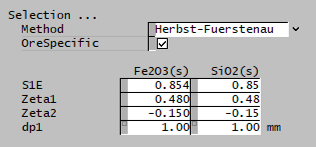
Method User The user specifies the selection function.
Herbst and Fuerstenau The Herbst and Fuerstenau selection function is used.
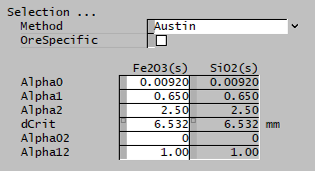
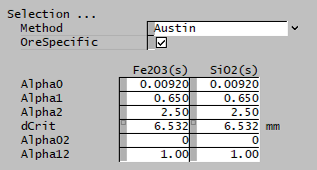
Austin The Austin selection function is used.
OreSpecific CheckBox Ore-specific parameters, allows the selection function to be separately input for all species. Default is all species have the same set of single input properties.
This option is only available if there is more than one species in the project with the size distribution property.
The fields below are only visible if Herbst-Fuerstenau is selected.
S1E Input Input parameter of the Herbst-Fuerstenau selection function.
Zeta1 Input Input parameter of the Herbst-Fuerstenau selection function.
Zeta2 Input Input parameter of the Herbst-Fuerstenau selection function.
dp1 Input Input parameter of the Herbst-Fuerstenau selection function.

MillHerbstFuerstenau5.png MillHerbstFuerstenau6.png

The fields below are only visible if Austin is selected.
Alpha0 Input Input parameter of the Austin selection function.
Alpha1 Input Input parameter of the Austin selection function.
Alpha2 Input Input parameter of the Austin selection function.
dCrit Input Input parameter of the Austin selection function.
Alpha02 Input Input parameter of the Austin selection function.
Alpha12 Input Input parameter of the Austin selection function.

MillHerbstFuerstenau7.png MillHerbstFuerstenau8.png

Breakage
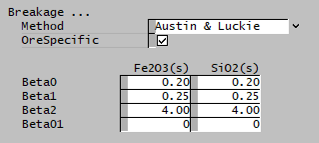
Method User The user specifies the breakage function.
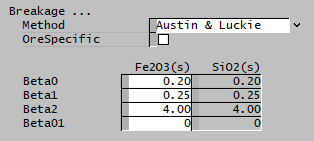
Austin and Luckie The Austin and Luckie breakage function is used.
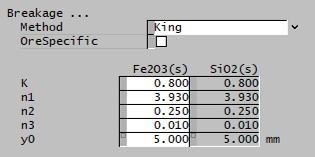
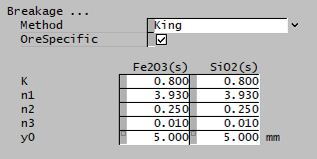
King The King selection function is used.
Natural Selection The Natural selection function is used.
OreSpecific CheckBox Ore-specific parameters, allows the breakage function to be separately input for all species. Default is all species have the same set of single input properties.
This option is only available if there is more than one species in the project with the size distribution property.
The fields below are only visible if Austin and Luckie is selected.
Beta0 Input Input parameter of the Austin and Luckie breakage function.
Beta1 Input Input parameter of the Austin and Luckie breakage function.
Beta2 Input Input parameter of the Austin and Luckie breakage function.
Beta01 Input Input parameter of the Austin and Luckie breakage function.

MillHerbstFuerstenau9.png MillHerbstFuerstenau10.png

The fields below are only visible if King is selected.
K Input Input parameter of the King breakage function.
n1 Input Input parameter of the King breakage function.
n2 Input Input parameter of the King breakage function.
n3 Input Input parameter of the King breakage function.
y0 Input Input parameter of the King breakage function.

MillHerbstFuerstenau11.png MillHerbstFuerstenau12.png

Results
CriticalSize / xc Display Critical size.
InterparComprAngle / alphaIP Display Interparticle compression angle.
Throughput / Gs Display Solids mass throughput flow rate of the HPGR.
RollsVelocity / U Display Circumferential velocity of the rolls.
RollsSpeed Display Rotational speed of the rolls.
SpecificThroughput / mDot Display Specific throughput parameter of the HPGR unit.
CompressionForce / F Display Compression force of the rolls.
GrossPower / P Display Gross power draw of the HPGR unit
SpecificEnergy / W Display Specific energy of grinding.

Selection page

The Selection page is used to specify or display the selection function values.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Distribution
Name Display Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream.
IntervalCount Display Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream.
SpWithPSDCount Display Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality.
Selection
Size Display Size of each interval in mesh series.
MeanSize Display Geometric mean size of each interval in mesh series.
Selection Input/Display Value of the selection function for each size interval, for each ore species.

Breakage page

The Breakage page is used to specify or display the breakage function values.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Distribution
Name Display Shows the name of the SysCAD Size Distribution (PSD) quality associated with the feed stream.
IntervalCount Display Shows the number of size intervals in the SysCAD Size Distribution (PSD) quality associated with the feed stream.
SpWithPSDCount Display Shows the number of species in the feed stream assigned with the SysCAD Size Distribution (PSD) quality.
Breakage
Size Display Size of each interval in internal mesh series.
Breakage Input/Display Value of the breakage function for each parent size interval, progeny size interval and ore species.

Power page

The Power page is used to display power draw of model blocks along the length of the rolls.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
Power
Position / y Display Position along the rolls length.
Power / Pk Display Power draw of model block at position along the rolls length.

About page

This page is provides product and licensing information about the Met Dynamics Models SysCAD Add-On.

Tag (Long/Short) Input / Display Description/Calculated Variables/Options
About
HelpLink ButtonLicensingHelp.png Opens a link to the Installation and Licensing page using the system default web browser. Note: Internet access is required.
Information ButtonCopyToClipboard.png Copies Product and License information to the Windows clipboard.
Product
Name Display Met Dynamics software product name
Version Display Met Dynamics software product version number.
BuildDate Display Build date and time of the Met Dynamics Models SysCAD Add-On.
License
File ButtonBrowse.png This is used to locate a Met Dynamics software license file.
Location Display Type of Met Dynamics software license or file name and path of license file.
SiteCode Display Unique machine identifier for license authorisation.
ReqdAuth Display Authorisation level required, MD-SysCAD Full or MD-SysCAD Runtime.
Status Display License status, LICENSE_OK indicates a valid license, other messages report licensing errors.
IssuedTo Display Only visible if Met Dynamics license file is used. Name of organisation/seat the license is authorised to.
ExpiryDate Display Only visible if Met Dynamics license file is used. License expiry date.
DaysLeft Display Only visible if Met Dynamics license file is used. Days left before the license expires.

Additional notes

When the edge stream is connected, the following applies to mass splits:

  • Solid species without a particle size distribution property are split to the edge stream according to the overall mass split of the default particle size distribution species selected in the SysCAD Project Configuration
  • If the default particle size distribution species is not present in the unit feed, the overall split of all other species with particle size distributions combined is used, as determined by the model.
  • Liquids species are split between the edge and product streams in the same proportion as solid species.
  • Gas phase species report directly to the product stream without split.

See also

References

  1. ↑ Torres, M. and Casali, A., 2009. A novel approach for the modelling of high-pressure grinding rolls. Minerals Engineering, 22(13), pp.1137-1146.
Retrieved from "https://wiki.metdynamics.com.au/index.php?title=HPGR_(Torres)&oldid=1725"