Partition (Size, Whiten and White)

Description

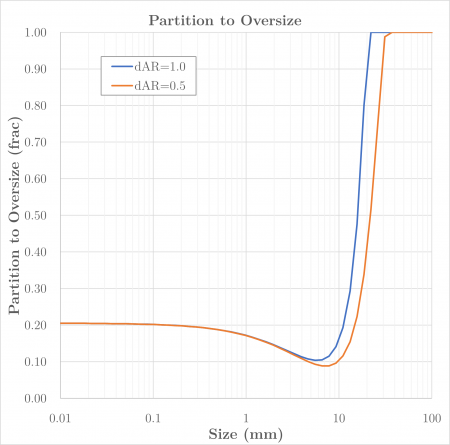
This article describes the Whiten and White (1977) expression for the partition of particles to oversize during screening. Several additions are made to the expression to reflect fines entrainment and particle shape.

The Whiten and White formulation is convenient for modelling screens as it implicitly honours the aperture size limit on particle passage, unlike other commonly used representations such as the Whiten efficiency curve or Rosin-Rammler equation.

Model theory

Figure 1. Screen partitions to oversize, with $D_{1}=50{\text{ mm}}$, $D_{2}=20{\text{ mm}}$, $R_{\rm {f}}=0.2$ and $\lambda =0.2$. Note how the particle aspect ratio, $d_{\rm {AR}}$, shifts the partition curve, allowing irregular particles to pass slotted apertures that would otherwise be retained.

The Whiten and White expression for recovery to screen oversize is:

$E_{{\rm {oc}}s}={\begin{cases}\exp(-n_{L}Lf_{\rm {o}}{\dfrac {{\big [}D_{1}-s{\big ]}{\big [}D_{2}-s{\big ]}}{D_{1}D_{2}}})&s<D_{2}\\1.0&s\geq D_{2}\\\end{cases}}$

where:

• $s$ is the diameter of a particle (mm)
• $E_{{\rm {oc}}s}$ is the corrected fraction of particles of size $s$ in the feed reporting to the oversize stream (frac)
• $n_{\rm {L}}$ is the number of trials per unit length parameter (/m)
• $L$ is the length of the screening area (or panel) in the direction of flow (m)
• $f_{\rm {o}}$ is the fraction open area of the screen deck/panels (m²/m²)
• $D_{1}$ is length (the longer side) of the screen deck/panel aperture (m)
• $D_{2}$ is width (the shorter side) of the screen deck/panel aperture (m)

Excel

The Whiten and White partition model may be invoked from the Excel formula bar with the following function call:

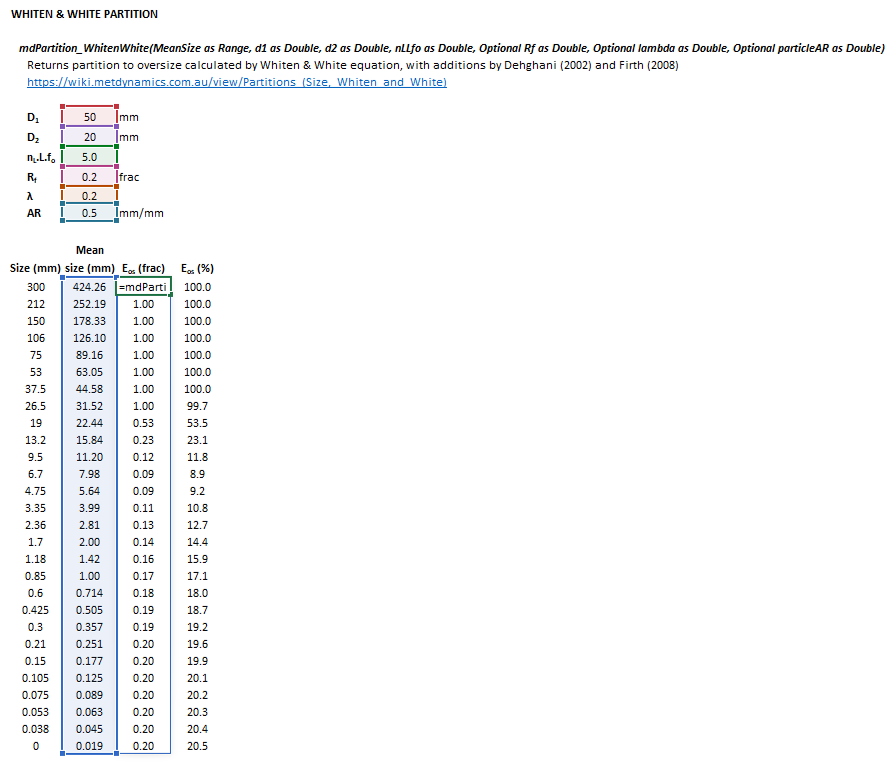
=mdPartition_WhitenWhite(MeanSize as Range, d1 as Double, d2 as Double, nLLfo as Double, Optional Rf as Double = 0, Optional lambda as Double = 0, Optional particleAR as Double = 1)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The input parameters and model results are defined below in matrix notation, along with an example image showing the selection of the same cells in the Excel interface:

${\begin{aligned}MeanSize&={\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{n}{\text{ (mm)}}\\\end{bmatrix}}\\\\d1&={\big [}D_{1}{\big ]}\\d2&={\big [}D_{2}{\big ]}\\nLLfo&={\big [}n_{\rm {L}}.L.f_{\rm {o}}{\big ]}\\Rf&={\big [}R_{\rm {f}}{\big ]}\\lambda&={\big [}\lambda {\big ]}\\particleAR&={\big [}d_{\rm {AR}}{\big ]}\\\end{aligned}}$

$mdPartition\_WhitenWhite={\begin{bmatrix}(E_{\rm {oa}})_{1}{\text{ (mm)}}\\\vdots \\(E_{\rm {oa}})_{n}{\text{ (mm)}}\\\end{bmatrix}}$

Figure 2. Example showing the selection of the input parameters (shaded cells), and Results (light blue frame) array in Excel.