Partition (Size, Whiten and White): Difference between revisions
Scott Munro (talk | contribs) m (1 revision imported) |
md>Scott.Munro m (→Model theory) |
||
| Line 9: | Line 9: | ||
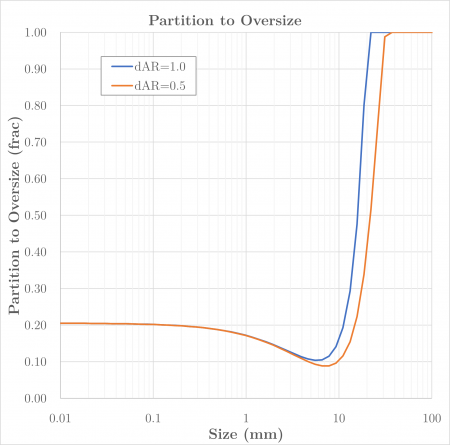
[[File:PartitionWhitenWhite1.png|thumb|450px|Figure 1. Screen partitions to oversize, with <math>D_1=50\text{ mm}</math>, <math>D_2=20\text{ mm}</math>, <math>R_{\rm f}=0.2</math> and <math>\lambda=0.2</math>. Note how the particle aspect ratio, <math>d_{\rm AR}</math>, shifts the partition curve, allowing irregular particles to pass slotted apertures that would otherwise be retained.]] | [[File:PartitionWhitenWhite1.png|thumb|450px|Figure 1. Screen partitions to oversize, with <math>D_1=50\text{ mm}</math>, <math>D_2=20\text{ mm}</math>, <math>R_{\rm f}=0.2</math> and <math>\lambda=0.2</math>. Note how the particle aspect ratio, <math>d_{\rm AR}</math>, shifts the partition curve, allowing irregular particles to pass slotted apertures that would otherwise be retained.]] | ||
The Whiten and | The Whiten and White expression for recovery to screen oversize is: | ||
{{Model theory (Text, Whiten and White Partition Curve)}} | |||
== Excel == | == Excel == | ||
Revision as of 12:35, 28 April 2023
Description
This article describes the Whiten and White (1977) expression for the partition of particles to oversize during screening.[1][2] Several additions are made to the expression to reflect fines entrainment and particle shape.
The Whiten and White formulation is convenient for modelling screens as it implicitly honours the aperture size limit on particle passage, unlike other commonly used representations such as the Whiten efficiency curve or Rosin-Rammler equation.
Model theory
The Whiten and White expression for recovery to screen oversize is:
where:
- is the diameter of a particle (mm)
- is the corrected fraction of particles of size in the feed reporting to the oversize stream (frac)
- is the number of trials per unit length parameter (/m)
- is the length of the screening area (or panel) in the direction of flow (m)
- is the fraction open area of the screen deck/panels (m2/m2)
- is length (the longer side) of the screen deck/panel aperture (m)
- is width (the shorter side) of the screen deck/panel aperture (m)
Whiten and White's equation was modified by Dehghani et al. (2002) to include a term for irregularly shaped particles, and is generalised to:[2]
where:
and is the representative aspect ratio of the particle population, the ratio of the second longest to the longest dimensions of a particle (mm/mm)
The aspect ratio property, , allows for the balanced screening of 'flaky' or 'elongated' particles on slotted meshes. Dehghani et al.'s relation reduces to Whiten and White's original equation when .
An average value of the partition is required when using size intervals. Whiten (1972) suggests the following averaging approach:[3]
where:
- is the index of the size interval, , is the number of size intervals
- is the corrected fraction of particles of size interval in the feed reporting to the oversize stream (frac)
- is the size of the square mesh at size interval (mm) that particles are retained on, in descending order such that
Numerical integration is applied to determine the average partition values of each size interval. Whiten's (1972) method is particularly useful when the partition curve is very steep, as may be the case for screens operating at high efficiency.
Firth and Hart (2008) suggested a simple modification to a partition curve to account for the observed entrainment of fine particles in an oversize stream, with decreasing probability as particle size increases:[4]
where:
- is the actual fraction of particles of size interval in the feed reporting to the oversize stream (frac)
- is the fraction of the finest particles or feed liquids split to the oversize stream (frac)
- is the geometric mean size of the size interval (mm)
- is the size constant
Excel
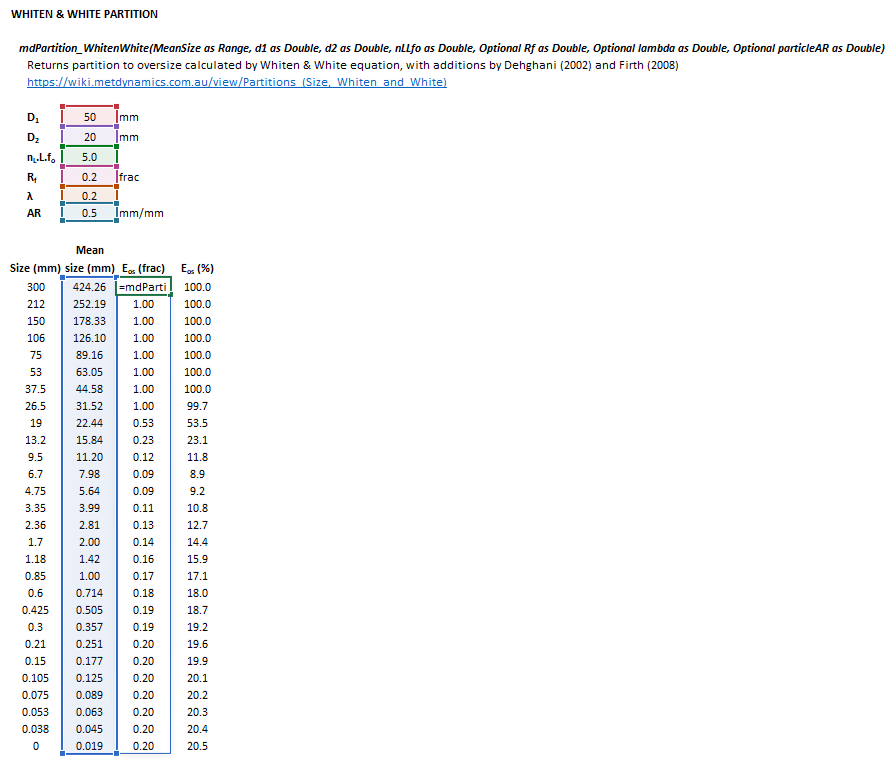
The Whiten and White partition model may be invoked from the Excel formula bar with the following function call:
=mdPartition_WhitenWhite(MeanSize as Range, d1 as Double, d2 as Double, nLLfo as Double, Optional Rf as Double = 0, Optional lambda as Double = 0, Optional particleAR as Double = 1)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and model results are defined below in matrix notation, along with an example image showing the selection of the same cells in the Excel interface:
|
|
|
|
SysCAD
References
- ↑ Whiten, W.J. and White, M.E., 1977. Modelling and simulation of high tonnage crushing plants. In: Proceedings of the 12th International Mineral Processing Congress, vol. II. Sao Paulo, pp. 148–158.
- ↑ 2.0 2.1 Dehghani, A., Monhemius, A.J. and Gochin, R.J., 2002. Evaluating the Nakajima et al. model for rectangular-aperture screens. Minerals engineering, 15(12), pp.1089-1094.
- ↑ Whiten, W.J., 1972. The simulation of crushing plants with models developed using multiple spline regression. Journal of the Southern African Institute of Mining and Metallurgy, 72(10), pp.257-264.
- ↑ Firth, B. and Hart, G., 2008. Some aspects of modeling partition curves for size classification. International journal of coal preparation and utilization, 28(3), pp.174-187.





![{\displaystyle E_{{\rm {oc}}s}={\begin{cases}\exp(-n_{L}Lf_{\rm {o}}{\dfrac {{\big [}D_{1}-s{\big ]}{\big [}D_{2}-s{\big ]}}{D_{1}D_{2}}})&s<D_{2}\\1.0&s\geq D_{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b064eb8f4289908faa6102b0d66e617f4de33c71)







![{\displaystyle E_{\rm {oc}}={\begin{cases}\exp(-n_{L}Lf_{\rm {o}}{\dfrac {{\big [}D_{1}-{\sqrt {2}}s\cos \theta {\big ]}{\big [}D_{2}-{\sqrt {2}}s\sin \theta {\big ]}}{D_{1}D_{2}}})&{\sqrt {2}}s\sin \theta <D_{2}\\1.0&{\sqrt {2}}s\sin \theta \geq D_{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16b7fc45ac593d5db6fee7f6afd973aa1545285f)














![{\displaystyle {\begin{aligned}MeanSize&={\begin{bmatrix}{\bar {d}}_{1}{\text{ (mm)}}\\\vdots \\{\bar {d}}_{n}{\text{ (mm)}}\\\end{bmatrix}}\\\\d1&={\big [}D_{1}{\big ]}\\d2&={\big [}D_{2}{\big ]}\\nLLfo&={\big [}n_{\rm {L}}.L.f_{\rm {o}}{\big ]}\\Rf&={\big [}R_{\rm {f}}{\big ]}\\lambda&={\big [}\lambda {\big ]}\\particleAR&={\big [}d_{\rm {AR}}{\big ]}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9304fdc803b8545ca8b6ab31aa443c59f1072e)