Partition (Size, Whiten-Beta)

Description

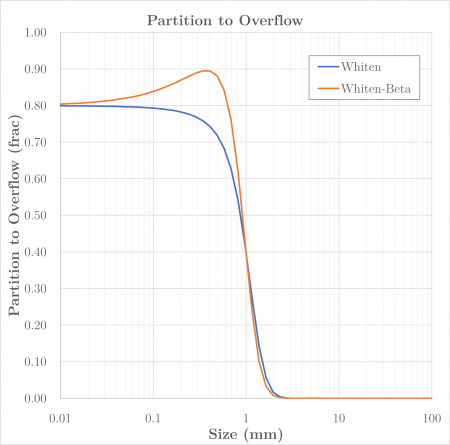
This article describes Whiten's expression for the efficiency of recovery to overflow, modified to represent observed 'fish hook' behaviour in the finer sizes.

Model theory

Figure 1. Whiten-Beta partitions to overflow, with (orange line) and without (blue line) use of the [math]\displaystyle{ \beta }[/math] parameter.

The Whiten-Beta expression for partition to overflow is:

[math]\displaystyle{ E_{\rm oa}(\bar d_i) = C \left [ \dfrac{ \left (1 + \beta \beta^* \dfrac{\bar d_i}{d_{\rm 50c}} \right )(\exp (\alpha) - 1)}{\exp \left ( \alpha \beta^* \dfrac{\bar d_i}{d_{\rm 50c}} \right ) + \exp (\alpha) - 2} \right ] }[/math]

where:

• [math]\displaystyle{ i }[/math] is the index of the size interval, [math]\displaystyle{ i = \{1,2,\dots,n\} }[/math], [math]\displaystyle{ n }[/math] is the number of size intervals
• [math]\displaystyle{ E_{\rm oa}(\bar d_i) }[/math] is the fraction of particles of size interval [math]\displaystyle{ i }[/math] in the feed reporting to the overflow stream (frac)
• [math]\displaystyle{ \bar d_{i} }[/math] is the geometric mean size of particles in size interval [math]\displaystyle{ i }[/math] (mm)
• [math]\displaystyle{ d_{\rm 50c} }[/math] is the corrected size at which 50% of the particle mass reports to underflow and 50% to overflow (mm)
• [math]\displaystyle{ C }[/math] is the fraction of feed liquids (or fines) split to overflow (frac)
• [math]\displaystyle{ \alpha }[/math] is a parameter representing the sharpness of separation
• [math]\displaystyle{ \beta }[/math] is a term introduced to accommodate the so-called fish-hook effect, and controls the initial rise in the efficiency curve at finer sizes
• [math]\displaystyle{ \beta^* }[/math] is computed to ensure the Whiten-Beta function preserves the definition of [math]\displaystyle{ d_{\rm 50c} }[/math] in the presence of the fish-hook, i.e. [math]\displaystyle{ E = 0.5 C }[/math] at [math]\displaystyle{ d_{\rm 50c} }[/math]

The value of [math]\displaystyle{ \beta^* }[/math] is not an input parameter and is computed numerically, by iteration, since by rearrangement:

[math]\displaystyle{ \beta^* = \dfrac{\ln \big[ \exp (\alpha) + 2 \beta \beta^* (\exp (\alpha) - 1) \big]}{\alpha} }[/math]

When the value of [math]\displaystyle{ \beta }[/math] is zero, the Whiten-Beta equation reverts to:

[math]\displaystyle{ E_{{\rm oa}i} = C \left [ \dfrac{ \exp (\alpha) - 1}{\exp \left ( \alpha \dfrac{\bar d_i}{d_{\rm 50c}} \right ) + \exp (\alpha) - 2} \right ] }[/math]

Excel

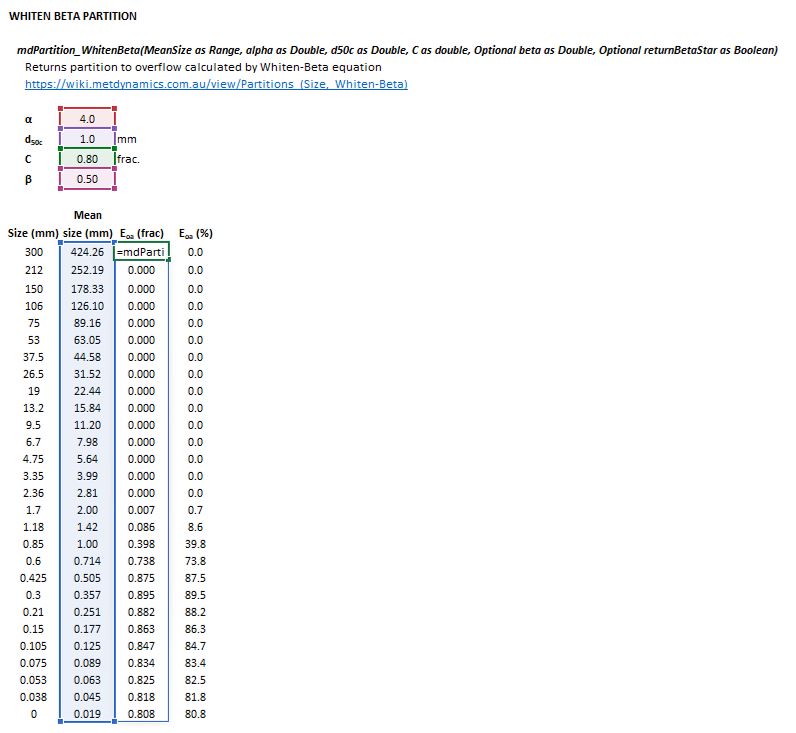
The Whiten-Beta efficiency curve model may be invoked from the Excel formula bar with the following function call:

=mdPartition_WhitenBeta(MeanSize as Range, alpha as Double, d50c as Double, C as double, Optional beta as Double = 0, Optional returnBetaStar as Boolean = false)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The input parameters and model results are defined below in matrix notation, along with an example image showing the selection of the same cells in the Excel interface:

[math]\displaystyle{ \begin{align} MeanSize & = \begin{bmatrix} \bar{d}_1\text{ (mm)}\\ \vdots\\ \bar{d}_n\text{ (mm)}\\ \end{bmatrix}\\ \\ alpha & = \big [\alpha \big ]\\ d50c & = \big [d_{50 \rm c} \text{ (mm)}\big ]\\ C & = \big [C\text{ (frac)}\big ]\\ Beta & = \big [\beta \big ]\\ returnBetaStar & = \big [(\text{True / False)} \big ]\\ \end{align} }[/math]	[math]\displaystyle{ mdPartition\_WhitenBeta = \begin{bmatrix} (E_{\rm oa})_1\text{ (frac)} & \beta^*\\ \vdots & [-] \\ (E_{\rm oa})_n\text{ (frac} & [-] \\ \end{bmatrix} }[/math]	Figure 2. Example showing the selection of the input parameters (shaded cells), and Results (light blue frame) array in Excel. The parameter [math]\displaystyle{ returnBetaStar=\text{False} }[/math] in this example.
where [math]\displaystyle{ \beta^* }[/math] is omitted from the results array if [math]\displaystyle{ returnBetaStar=\text{False} }[/math].

SysCAD

The Whiten-Beta partition is available from the MetDynamics*Hydrocyclone unit model.

The sections and variable names used in the SysCAD interface are described in detail in the following tables.

Cyclone page

The Cyclone page is used to specify the input parameters for the hydrocyclone model.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
WhitenBeta
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
OreSpecific	CheckBox	Ore-specific partitions, allows the Whiten-Beta equation parameters to be separately input for all species. Default is all species have the same set of single input properties. This option is only available if there is more than one species in the project with the size distribution property.
Alpha	Input	The Whiten-Beta equation alpha parameter.
d50c	Input	The Whiten-Beta equation d50c corrected cut size parameter.
C	Input	The Whiten-Beta equation C parameter.
Beta	Input	The Whiten-Beta equation beta parameter.
Beta*	Display	The Whiten-Beta equation Beta* parameter corresponding to the selected value of Beta.
Liquids
LiquidsSeparMethod	Split To UF (User)	Liquids are split to underflow by a user-defined fraction of liquids in the feed.
	Split To UF (1-C)	Liquids are split to underflow by the C (overflow) fraction specified for the first species in the model.
	UF Solids Fraction	Sufficient liquids mass is recovered to the underflow stream to yield the user-defined underflow solids mass fraction value (if possible).
	UF Liquids Fraction	Sufficient liquids mass is recovered to the underflow stream to yield the user-defined underflow liquids mass fraction value (if possible).
UFSolidsFracReqd / UF.SfReqd	Input	Required value of the mass fraction of solids in the underflow stream. Only visible if UF Solids Fraction is selected.
UFLiquidsFracReqd / UF.LfReqd	Input	Required value of the mass fraction of liquids in the underflow stream. Only visible if UF Liquids Fraction is selected.
LiqSplitToUF / UF.LiqSplit	Input/Display	The fraction of liquids recovered to underflow.