Blasting (KCO)

Description

This article describes the Kuznetsov–Cunningham–Ouchterlony (KCO) model (Ouchterlony, 2005), also known as the Swebrec function, for predicting rock fragmentation by blasting.

Model theory

This section is currently under construction. Please check back later for updates and revisions.

Excel

The KOC blasting model may be invoked from the Excel formula bar with the following function call:

=mdUnit_Blasting_KCO(Parameters as Range, Size as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

Inputs

The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row ([math]\displaystyle{ i }[/math]) x column ([math]\displaystyle{ j }[/math]) format:

[math]\displaystyle{ Parameters= \begin{bmatrix} H\text{ (m)}\\ B\text{ (m)}\\ S\text{ (m)}\\ \phi_{\rm h}\text{ (m)}\\ L_{\rm b}\text{ (m)}\\ L_{\rm c}\text{ (m)}\\ L_{\rm Tot}\text{ (m)}\\ \sigma\text{ (m)}\\ Q\text{ (kg)}\\ q\text{ (kg/m}^3\text{)}\\ s_{\rm ANFO}\text{ (}%\text{)}\\ \rho\text{ (t/m}^3\text{)}\\ \sigma_{\rm c}\text{ (MPa)}\\ E\text{ (GPa)}\\ \text{In-situ block size (m)}\\ \text{RMD}\\ \end{bmatrix},\;\;\;\;\;\; Size = \begin{bmatrix} d_{1}\text{ (mm)}\\ \vdots\\ d_n\text{ (mm)}\\ \end{bmatrix} }[/math]

where:

• [math]\displaystyle{ H }[/math] is the bench height or hole depth (m)
• [math]\displaystyle{ B }[/math] is Burden (m)
• [math]\displaystyle{ S }[/math] is Spacing (m)
• [math]\displaystyle{ \phi_{\rm h} }[/math] is drill hole diameter (m)
• [math]\displaystyle{ L_{\rm b} }[/math] is the length of bottom charge (m)
• [math]\displaystyle{ L_{\rm c} }[/math] is the length of column charge (m)
• [math]\displaystyle{ L_{\rm Tot} }[/math] is the total charge length, (m)
• [math]\displaystyle{ \sigma }[/math] is the standard deviation drilling accuracy (m)
• [math]\displaystyle{ Q }[/math] is Charge weight per hole (kg)
• [math]\displaystyle{ q }[/math] is Specific charge (kg/m³)
• [math]\displaystyle{ s_{\rm ANFO} }[/math] is ANFO relative weight strength (%)
• [math]\displaystyle{ \rho }[/math] is rock density (t/m³)
• [math]\displaystyle{ \sigma_{\rm c} }[/math] is compressive strength (MPa)
• [math]\displaystyle{ E }[/math] is Young's modulus (GPa)
• [math]\displaystyle{ \text{In-situ block size} }[/math] is in situ block size (m)
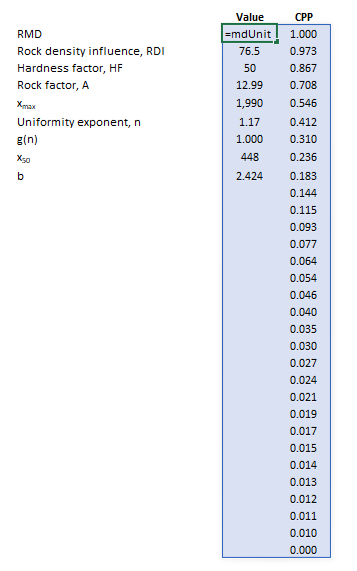
• [math]\displaystyle{ \text{RMD} }[/math] is Rock Mass Description
• [math]\displaystyle{ n }[/math] is the number of size intervals
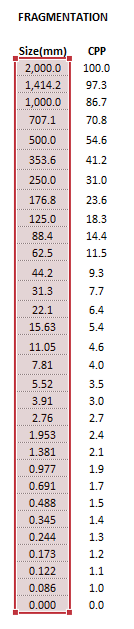
• [math]\displaystyle{ d_i }[/math] is the size of the square mesh interval that mass is retained on (mm)
• [math]\displaystyle{ d_{i+1}\lt d_i\lt d_{i-1} }[/math], i.e. descending size order from top size ([math]\displaystyle{ d_{1} }[/math]) to sub mesh ([math]\displaystyle{ d_{n}=0 }[/math] mm)

Results

The results are displayed in Excel as an array corresponding to the matrix notation below:

[math]\displaystyle{ \mathit{mdUnit\_Blasting\_KCO} = \begin{bmatrix} \begin{bmatrix} \text{RMD}\\ H_{\rm f}\\ x_{\rm Max}\text{ (mm)}\\ n\\ g(h)\\ x_{50}\text{ (mm)}\\ b\\ \end{bmatrix} & \begin{array}{c} \begin{bmatrix} \mathit{CFP}_1\text{ (w/w)}\\ \vdots\\ \mathit{CFP}_n\text{ (w/w)} \end{bmatrix} \\ \\ \\ \\ \end{array} \end{bmatrix} }[/math]

where:

• [math]\displaystyle{ H_{\rm f} }[/math] is the hardness factor
• [math]\displaystyle{ x_{\rm Max} }[/math] is the maximum size parameter of the Swebrec function (mm)
• [math]\displaystyle{ n }[/math] is the uniformity exponent parameter of the Swebrec function
• [math]\displaystyle{ g(n) }[/math] is a function parameter of the Swebrec function
• [math]\displaystyle{ x_{\rm 50} }[/math] is the mean size parameter of the Swebrec function (mm)
• [math]\displaystyle{ b }[/math] is an exponent parameter of the Swebrec function
• [math]\displaystyle{ \mathit{CFP}_i }[/math] is the cumulative fraction passing size interval [math]\displaystyle{ i }[/math] (w/w)

Example

The images below show the selection of input arrays and output results in the Excel interface.

Figure 1. Example showing the selection of the Parameters (blue frame) array in Excel.

Figure 2. Example showing the selection of the Size (red frame) array in Excel.

Figure 3. Example showing the selection of the Results (light blue frame) array in Excel.