Stirred Mill (Power, Heath)

Description

This article describes the Heath (Heath et al. 2017) method for estimating the power draw of a High Intensity Grinding (HIG) stirred mill.

Model theory

This section is currently under construction. Please check back later for updates and revisions.

Excel

The Heath HIG stirred mill power model may be invoked from the Excel formula bar with the following function call:

=mdMillPower_Heath(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Parameters= \begin{bmatrix} d_{\rm ID}\text{ (m)}\\ d_{\rm r}\text{ (m)}\\ d_{\rm s}\text{ (m)}\\ h_{\rm b}\text{ (m)}\\ n_{\rm d}\\ d_{\rm b}\text{ (m)}\\ \rho_{\rm m}\text{ (v/v)}\\ \rho_{\rm b}\text{ (t/m}^3\text{)}\\ \rho_{\rm s}\text{ (t/m}^3\text{)}\\ \mu\text{ (N.s/m}^2\text{)}\\ Q\text{ (m}^3\text{/s)}\\ N_{\rm r}\text{ (rpm)}\\ \end{bmatrix},\;\;\;\;\;\; \mathit{mdMillPower\_Heath} = \begin{bmatrix} P\text{ (kW)}\\ \text{Iterations}\\ v_{\rm r}\text{ (m/s)}\\ \text{Re}\\ U_{\rm s}\text{ (m/s)}\\ U_{\rm slip}\text{ (m/s)}\\ U_{\rm rise}\text{ (m/s)}\\ \rho_{\rm s,g}\text{ (t/m}^3\text{)}\\ \rho_{\rm s,c}\text{ (t/m}^3\text{)}\\ \end{bmatrix}\;\;\;\;\;\;\;\;\;\;\;\; } where: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{\rm ID}} is the internal diameter of the mill (m) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{\rm r}} is the rotor tip diameter (m) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{\rm s}} is the rotor shaft diameter (m) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{\rm b}} is the height of the bead bed (m) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{\rm d}} is the number of submerged discs Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{\rm b}} is the bead diameter (m) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\rm m}} is the fraction of mill volume occupied by beads (v/v) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm b}} is the density of the grinding beads (t/m3) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm s}} is the density of slurry (t/m3) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} is the slurry viscosity (N.s/m2) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} is the volumetric flow rate of slurry feed to the mill (m3/s) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{\rm r}} is the rotational speed of the rotor (rpm) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} is mill power (kW) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Iterations}} is the number of internal iterations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{\rm r}} is the rotor tip velocity (m/s) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Re}} is the Reynolds Number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm s}} is the Stokes settling rate (m/s) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm slip}} is is the slip velocity (m/s) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm rise}} is the rise velocity (m/s) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm s,g}} is the solids pressure due to gravity (N/m2) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm s,c}} is the solids pressure due to centrifugal force (N/m2)

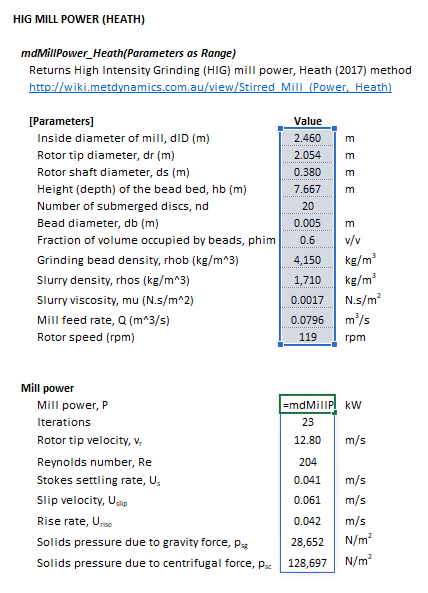Figure 1. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

This section is currently under construction. Please check back later for updates and revisions.