Fine Wet Screen (Mwale)

Description

This article describes an implementation of the Mwale (Mwale et al., 2016) model for fine wet screening.

Model theory

This section is currently under construction. Please check back later for updates and revisions.

Excel

The Mwale fine wet screen model may be invoked from the Excel formula bar with the following function call:

=mdUnit_Screen_Mwale(Parameters as Range, Size as Range, Feed as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

Inputs

The required inputs are defined below in matrix notation with elements corresponding to cells in Excel row ([math]\displaystyle{ i }[/math]) x column ([math]\displaystyle{ j }[/math]) format:

[math]\displaystyle{ Parameters= \begin{bmatrix} K\text{ (t/h.m}^2\text{)}\\ \delta\text{ ((t/h)}^{-1}\text{)}\\ \alpha\text{ (-)}\\ A_{\rm o}\text{ (m}^2\text{)}\\ x_{\rm a} \text{ (mm)}\\ s\text{ (w/w)}\\ \end{bmatrix},\;\;\;\;\;\; Size = \begin{bmatrix} d_{1}\text{ (mm)}\\ \vdots\\ d_n\text{ (mm)}\\ \end{bmatrix},\;\;\;\;\;\; Feed= \begin{bmatrix} (Q_{\rm M,F})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{1m}\text{ (t/h)}\\ \vdots & \ddots & \vdots\\ (Q_{\rm M,F})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,F})_{nm}\text{ (t/h)}\\ \end{bmatrix} }[/math]

where:

• [math]\displaystyle{ K }[/math] is the kinetic parameter (t/h.m²)
• [math]\displaystyle{ \delta }[/math] is a bypass parameter ((t/h)^-1)
• [math]\displaystyle{ \alpha }[/math] is the sharpness parameter (-)
• [math]\displaystyle{ A_{\rm o} }[/math] is the screen open area (m²)
• [math]\displaystyle{ x_{\rm a} }[/math] is the screen aperture (mm)
• [math]\displaystyle{ s }[/math] is the mass fraction of solids in the feed slurry (w/w)
• [math]\displaystyle{ n }[/math] is the number of size intervals
• [math]\displaystyle{ d_i }[/math] is the size of the square mesh interval that feed mass is retained on (mm)
• [math]\displaystyle{ d_{i+1}\lt d_i\lt d_{i-1} }[/math], i.e. descending size order from top size ([math]\displaystyle{ d_{1} }[/math]) to sub mesh ([math]\displaystyle{ d_{n}=0 }[/math] mm)
• [math]\displaystyle{ m }[/math] is the number of ore types
• [math]\displaystyle{ Q_{\rm M,F} }[/math] is feed solids mass flow rate by size and ore type (t/h)

Results

The results are displayed in Excel as an array corresponding to the matrix notation below:

[math]\displaystyle{ \mathit{mdUnit\_Screen\_Mwale} = \begin{bmatrix} \begin{array}{c} \begin{bmatrix} E_{\rm US}\\ \end{bmatrix} \\ \\ \\ \end{array} & \begin{bmatrix} \bar d_1\text{ (mm)}\\ \vdots\\ \bar d_n\text{ (mm)} \end{bmatrix} & \begin{bmatrix} (Q_{\rm M,OS})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,OS})_{1m}\text{ (t/h)}\\ \vdots & \ddots & \vdots\\ (Q_{\rm M,OS})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,OS})_{nm}\text{ (t/h)}\\ \end{bmatrix} & \begin{bmatrix} (Q_{\rm M,US})_{11}\text{ (t/h)} & \dots & (Q_{\rm M,US})_{1m}\text{ (t/h)}\\ \vdots & \ddots & \vdots\\ (Q_{\rm M,US})_{n1}\text{ (t/h)} & \dots & (Q_{\rm M,US})_{nm}\text{ (t/h)}\\ \end{bmatrix} & \begin{bmatrix} (E_{\rm oa})_1\text{ (frac)}\\ \vdots\\ (E_{\rm oa})_n\text{ (frac)} \end{bmatrix} \end{bmatrix} }[/math]

where:

• [math]\displaystyle{ E_{\rm US} }[/math] is the efficiency of undersize removal achieved by the screen (frac)
• [math]\displaystyle{ \bar d_{i} }[/math] is the geometric mean size of particles in size interval [math]\displaystyle{ i }[/math] (mm)
• [math]\displaystyle{ Q_{\rm M,OS} }[/math] is mass flow rate of solids to the oversize stream (t/h)
• [math]\displaystyle{ Q_{\rm M,US} }[/math] is mass flow rate of solids to the undersize stream (t/h)
• [math]\displaystyle{ E_{\rm oa} }[/math] is the partition to oversize (frac)

Example

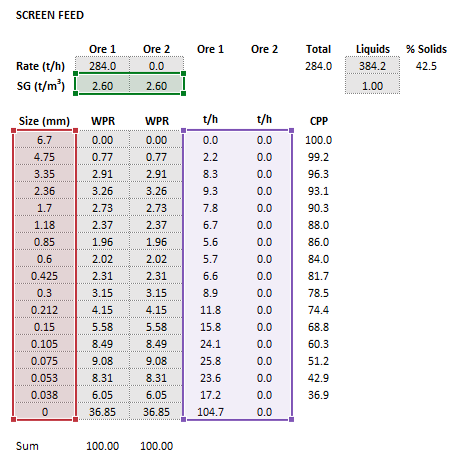
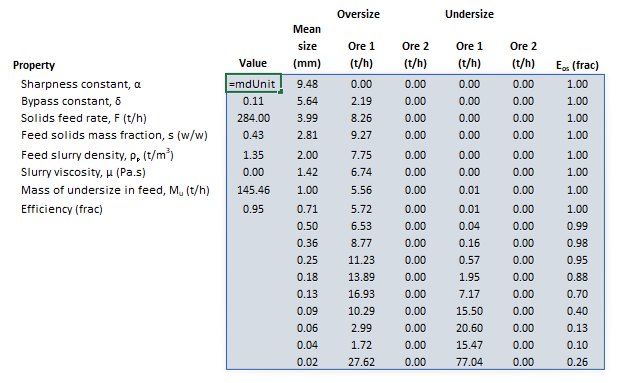
The images below show the selection of input arrays and output results in the Excel interface.

Figure 1. Example showing the selection of the Parameters (blue frame) array in Excel.

Figure 2. Example showing the selection of the Size (red frame), and Feed (purple frame) arrays in Excel.

Figure 3. Example showing the outline of the Results (light blue frame) array in Excel.

SysCAD

This section is currently under construction. Please check back later for updates and revisions.