Stirred Mill (Power, Heath)

Description

This article describes the Heath et al. (2017) method for estimating the power draw of a castellated rotor High Intensity Grinding stirred mill (HIGmill).

Model theory

Heath et al. (2017) proposed the following relationship for the power draw, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} (kW), of a HIGmill with castellated rotors:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = k_1 \cdot n_{\rm d} {d_{\rm r}}^{k_2} {v_t}^{k_3} ( p_{\rm s,g} + k_4 p_{\rm s,c})}

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{\rm d}} is the number of submerged discs
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{\rm r}} is the rotor tip diameter (m)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{\rm t}} is the rotor tip velocity (m/s)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{\rm s,g}} is the solids pressure due to gravity (N/m²)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{\rm s,c}} is the solids pressure due to centrifugal force (N/m²)

and $k_{1}-k_{4}$ have the values shown in Table 1.

Coefficients and exponents of the Heath et al. power equation.

Coefficient or exponent	Value
$k_{1}$	0.000197
$k_{2}$	1.3
$k_{3}$	0.8
$k_{4}$	0.15

The solids pressure due to centrifugal force, $\rho _{\rm {s,c}}$ (N/m²), is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{\rm s,c} = \frac{4}{3} \pi^2 \omega^2 \left (\rho_{\rm b} - \rho_{\rm s} \right ) \left ({r_{\rm rotor}}^2 - {r_{\rm shaft}}^2 \right )}

where:

• $\omega$ is the rotation rate of the rotor (rps)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm b}} is the density of the grinding beads (t/m³)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm s}} is the density of slurry (t/m³)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{\rm rotor}} is the rotor tip radius (m), i.e Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.5d_{\rm r}}
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{\rm shaft}} is the rotor shaft radius (m)

The solids pressure due to gravity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\rm s,g}} (N/m²), is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{\rm s,g} = \begin{cases} 0.5 g h_{\rm b} \left (\rho_{\rm b} - \rho_{\rm s} \right ) \left ( 1 - \dfrac{U_{\rm slip}}{U_{\rm rise}} \right ) & U_{\rm slip} < U_{\rm rise}\\ 0 & U_{\rm slip} \geq U_{\rm rise}\\ \end{cases} }

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h_{\rm b}} is the height of the bead bed (m)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm slip}} is is the slip velocity (m/s)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm rise}} is the rise velocity (m/s)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} is acceleration due to gravity (m/s²)

The rise velocity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm rise}} (m/s) is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm rise} = \dfrac{Q}{\pi \left ( \dfrac{d_{\rm ID}}{2} \right )^2 (1 - \phi_{\rm m})}}

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} is the volumetric flow rate of slurry feed to the mill (m³/s)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{\rm ID}} is the internal diameter of the mill (m)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\rm m}} is the fraction of the charge volume (i.e. bead bed) occupied by beads (v/v)

The slip velocity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm slip}} (m/s) is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm slip} = \dfrac{U_{\rm s} \phi_{\rm m}}{1 - \phi_{\rm m}}}

The Stokes settling rate, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm slip}} (m/s), is determined from:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm s} = \dfrac{ {d_{\rm b}}^2 g (\rho_{\rm b} - \rho_{\rm s} ) (1 - \phi_{\rm m})^{4.65} }{18 \mu \left ( 1 + 0.15 \mathrm{Re}^{0.687} \right )}}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re} = \dfrac{ d_{\rm b} \rho_{\rm s} U_{\rm s}}{\mu}}

where:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{\rm b}} is the bead diameter (m)
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} is the slurry viscosity (N.s/m²)

The Reynolds number, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re}} , requires the settling velocity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\rm s}} , which itself requires the Reynolds number. Therefore an iterating numerical solution is necessary to resolve the slip velocity.

Additional notes

The Heath et al. (2017) publication appears to contain a printing error, where the value of coefficient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_4} is inadvertently referred to as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_2} .

Furthermore, the coefficient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1} appears twice, in both the equations for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{\rm s,c}} . The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{\rm s,c}} term itself also appears in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} and is adjusted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_4} , making the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1} repetition unusual, and somewhat redundant. It is probable that the presence of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1} in the equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{\rm s,c}} is also a printing error and should be omitted. This is supported by application of the power model to industrial HIGmill specifications, which produces an appropriate result only with the equations as presented above.

Excel

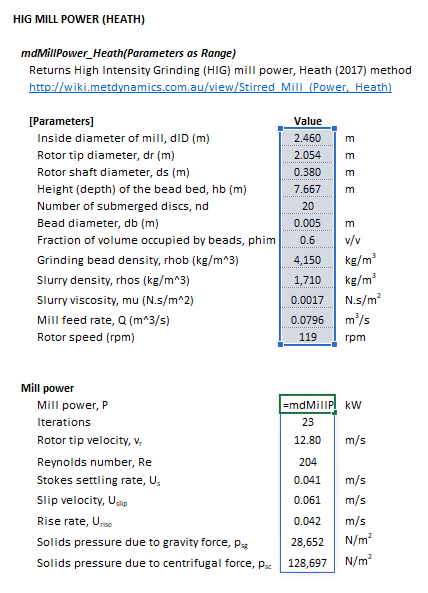
The Heath HIG stirred mill power model may be invoked from the Excel formula bar with the following function call:

=mdMillPower_Heath(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Parameters= \begin{bmatrix} d_{\rm ID}\text{ (m)}\\ d_{\rm r}\text{ (m)}\\ d_{\rm s}\text{ (m)}\\ h_{\rm b}\text{ (m)}\\ n_{\rm d}\\ d_{\rm b}\text{ (m)}\\ \phi_{\rm m}\text{ (v/v)}\\ \rho_{\rm b}\text{ (t/m}^3\text{)}\\ \rho_{\rm s}\text{ (t/m}^3\text{)}\\ \mu\text{ (N.s/m}^2\text{)}\\ Q\text{ (m}^3\text{/s)}\\ N_{\rm r}\text{ (rpm)}\\ \end{bmatrix},\;\;\;\;\;\; \mathit{mdMillPower\_Heath} = \begin{bmatrix} P\text{ (kW)}\\ \text{Iterations}\\ v_{\rm t}\text{ (m/s)}\\ \text{Re}\\ U_{\rm s}\text{ (m/s)}\\ U_{\rm slip}\text{ (m/s)}\\ U_{\rm rise}\text{ (m/s)}\\ p_{\rm s,g}\text{ (N/m}^2\text{)}\\ p_{\rm s,c}\text{ (N/m}^2\text{)}\\ \end{bmatrix}\;\;\;\;\;\;\;\;\;\;\;\; } where: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_{\rm r}} is the rotational speed of the rotor (rpm), i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega \times 60} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{\rm s}} is the rotor shaft diameter (m), i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 r_{\rm rotor}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Iterations}} is the number of internal iterations

Figure 1. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Heath power model is an optional calculation for stirred mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
Heath
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
MillDiameter	Input/Display	Inside diameter of the mill.
RotorTipDiameter	Input/Display	Diameter of the rotor at the tip.
RotorShaftDiameter	Input	Diameter of the rotor shaft.
MediaBedHeight	Input/Display	Height of the media (bead) bed.
NumSubmergedDiscs	Input	Number of submerged discs.
MediaDiameter	Input/Display	Diameter of the media (beads).
MediaVolFrac	Input	Volume fraction of media solids in the charge/bed.
MediaDensity	Input	Density of media.
SlurryDensity	Display	Density of slurry in the feed (or load for Dynamic).
SlurryViscosity	Input	Dynamic viscosity of slurry.
Feed.SLVolFlow / Feed.SLQv	Display	Volumetric flow rate of slurry into the mill.
RotorSpeed	Input/Display	Rotational speed of the rotor.
Iterations	Display	Number of internal iterations required to solve settling velocity equations.
RotorTipVelocity	Display	Velocity of the rotor at the tip.
ReynoldsNumber / Re	Display	Reynolds number.
SettlingVelocity / Us	Display	Stokes settling velocity.
SlipVelocity / Uslip	Display	Fluid slip velocity.
RiseVelocity / Urise	Display	Fluid rise velocity.
GravityPressure / psg	Display	Pressure due to gravitational force.
CentrifugalPressure / psc	Display	Pressure due to centrifugal force.
GrossPower	Display	Gross power drawn by the mill.