Time Series Analysis (CUSUM): Difference between revisions
Jump to navigation
Jump to search
Scott Munro (talk | contribs) m (1 revision imported) |
md>Scott.Munro m (→Excel) |
||
| Line 9: | Line 9: | ||
== Excel == | == Excel == | ||
The '''CUSUM''' control chart may be invoked from the Excel formula bar with the following function calls: | |||
The CUSUM control chart may be invoked from the Excel formula bar with the following function calls: | |||
<syntaxhighlight lang="vb">=mdTimeSeries_CUSUM(TimeSeriesData as Range, T as Double, Optional k as Double = 0)</syntaxhighlight> | <syntaxhighlight lang="vb">=mdTimeSeries_CUSUM(TimeSeriesData as Range, T as Double, Optional k as Double = 0)</syntaxhighlight> | ||
{{Excel (Text, Help, No Arguments)}} | {{Excel (Text, Help, No Arguments)}} | ||
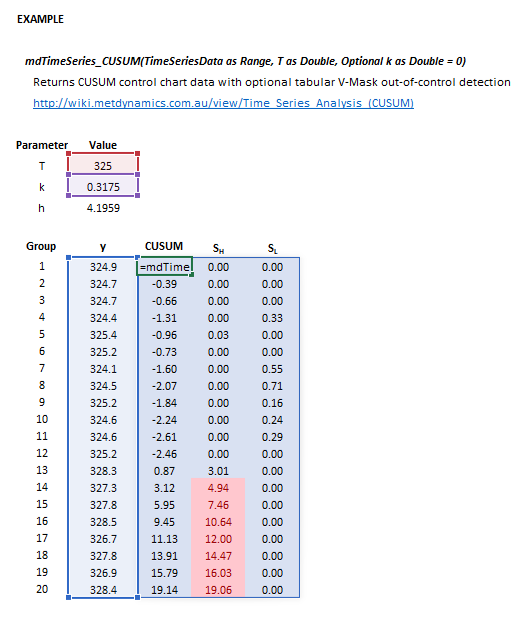
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface: | |||
{| | |||
|- style="vertical-align:top;" | |||
| | |||
{| | |||
|- style="vertical-align:top;" | |||
| | |||
:<math> | |||
\begin{align} | |||
\mathit{TimeSeriesData} & = | |||
\begin{bmatrix} | |||
y_1\\ | |||
\vdots\\ | |||
y_t\\ | |||
\end{bmatrix}\\ | |||
\\ | |||
\mathit{T} & = \big [ T \big ]\\ | |||
\\ | |||
\mathit{k} & = \big [ k \big ]\\ | |||
\end{align}</math> | |||
| | |||
::<math> | |||
\begin{align} | |||
\mathit{mdTimeSeries\_CUSUM} & = | |||
\begin{bmatrix} | |||
\begin{bmatrix} | |||
C_{1}\\ | |||
\vdots\\ | |||
C_{t}\\ | |||
\end{bmatrix} | |||
& | |||
\begin{bmatrix} | |||
S_{\rm H,1}\\ | |||
\vdots\\ | |||
S_{\rm H,t}\\ | |||
\end{bmatrix}^* | |||
& | |||
\begin{bmatrix} | |||
S_{\rm L,1}\\ | |||
\vdots\\ | |||
S_{\rm L,t}\\ | |||
\end{bmatrix}^* | |||
\end{bmatrix} | |||
\end{align} | |||
</math> | |||
|- style="vertical-align:top;" | |||
|colspan="2"| | |||
where: | |||
* <math>y_t</math> is the original observation (data point) at time <math>t</math> | |||
* <math>T</math> is a constant, typically a target value or the mean of historical data | |||
* <math>k</math> is the slope of the V-Mask arm, an optional parameter (V-Mask limits <math>S_{\rm H}</math> and <math>S_{\rm L}</math> are not returned if <math>k</math> is omitted) | |||
* <math>C_t</math> is the value of the cumulative sum (CUSUM) at time <math>t</math> | |||
* <math>S_{\rm H}</math> and <math>S_{\rm L}</math> are the high and low V-Mask parameters, respectively, and the <math>^*</math> superscripts indicate they are optionally-returned | |||
|} | |||
| | |||
:[[File:TimeSeriesAnalysis2.png|frame|Figure 1. Example showing the selection of the '''TimeSeriesData''' (blue frame), '''T''' (red frame), '''k''' (purple frame), and Results (light blue frame) arrays in Excel. The <math>S_{\rm L}</math> and <math>S_{\rm L}</math> parameters are returned in this example as '''k''' is specified.]] | |||
|} | |||
== References == | == References == | ||
Revision as of 03:29, 19 May 2023
Description
This article describes a method for preparing a Cumulative Sum (CUSUM) control chart.[1][2]
Model theory
Excel
The CUSUM control chart may be invoked from the Excel formula bar with the following function calls:
=mdTimeSeries_CUSUM(TimeSeriesData as Range, T as Double, Optional k as Double = 0)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
References
- ↑ NIST/SEMATECH, 2012. e-Handbook of Statistical Methods, http://www.itl.nist.gov/div898/handbook/, accessed 24 March 2022.
- ↑ Napier-Munn, T.J., 2014. Cunning solutions to process improvement. 12th Mill Operators' Conference, Townsville, Qld, 1-3 September 2014.