Interpolation: Difference between revisions
Jump to navigation
Jump to search
Scott Munro (talk | contribs) m (1 revision imported) |
md>Scott.Munro m (→Model theory) |
||
| Line 8: | Line 8: | ||
== Excel == | == Excel == | ||
The interpolation methods may be invoked from the Excel formula bar with the following function calls: | The interpolation methods may be invoked from the Excel formula bar with the following function calls: | ||
<syntaxhighlight lang="vb">=mdInterp_Linear(known_xs as Range, known_ys as Range, xs as Range)</syntaxhighlight> | <syntaxhighlight lang="vb">=mdInterp_Linear(known_xs as Range, known_ys as Range, xs as Range)</syntaxhighlight> | ||
and | |||
<syntaxhighlight lang="vb">=mdInterp_CubicSpline(known_xs as Range, known_ys as Range, xs as Range)</syntaxhighlight> | <syntaxhighlight lang="vb">=mdInterp_CubicSpline(known_xs as Range, known_ys as Range, xs as Range)</syntaxhighlight> | ||
{{Excel (Text, Help, No Arguments)}} | {{Excel (Text, Help, No Arguments)}} | ||
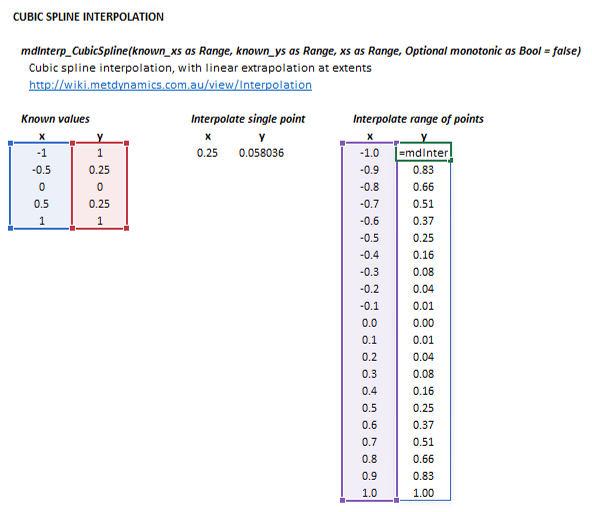
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface: | |||
{| | |||
|- style="vertical-align:top;" | |||
| | |||
{| | |||
|- style="vertical-align:top;" | |||
| | |||
:<math> | |||
\begin{align} | |||
\mathit{known\_xs} = | |||
\begin{bmatrix} | |||
x_1\\ | |||
\vdots\\ | |||
x_n\\ | |||
\end{bmatrix},\;\;\;\; | |||
\mathit{known\_ys} = | |||
\begin{bmatrix} | |||
y_1\\ | |||
\vdots\\ | |||
y_n\\ | |||
\end{bmatrix},\;\;\;\; | |||
\mathit{xs} = | |||
\begin{bmatrix} | |||
x_1\\ | |||
\vdots\\ | |||
x_m\\ | |||
\end{bmatrix}\;\;\;\; | |||
\end{align}</math> | |||
|<math> | |||
\begin{align} | |||
\mathit{mdInterp\_Linear} & = | |||
\begin{bmatrix} | |||
y_1\\ | |||
\vdots\\ | |||
y_m\\ | |||
\end{bmatrix}\\ | |||
\\ | |||
\mathit{mdInterp\_CubicSpline} & = | |||
\begin{bmatrix} | |||
y_1\\ | |||
\vdots\\ | |||
y_m\\ | |||
\end{bmatrix} | |||
\end{align} | |||
</math> | |||
|- style="vertical-align:top;" | |||
|colspan="2"| | |||
where: | |||
* <math>n</math> is the number of data points | |||
* <math>m</math> is the number of interpolation points | |||
* <math>x_1 \cdots x_n</math> is an array of the known independent data values | |||
* <math>y_1 \cdots y_n</math> is an array of the known dependent data values | |||
* <math>x_1 \cdots x_m</math> is an array of the independent data values at which the dependant variable is to be interpolated | |||
* <math>y_1 \cdots y_m</math> is an array of the interpolated dependant variable values | |||
|} | |||
| | |||
::[[File:Interpolation1.png|frame|Figure 1. Example showing the selection of the '''known_xs''' (blue frame), '''known_ys''' (red frame), '''xs''' (purple frame), and '''Results''' (light blue frame) arrays in Excel.]] | |||
|} | |||
== References == | == References == | ||
[[Category:Excel]] | [[Category:Excel]] | ||
Revision as of 09:54, 17 May 2023
Description
This article describes linear and cubic spline data interpolation methods.
Model theory
Excel
The interpolation methods may be invoked from the Excel formula bar with the following function calls:
=mdInterp_Linear(known_xs as Range, known_ys as Range, xs as Range)
and
=mdInterp_CubicSpline(known_xs as Range, known_ys as Range, xs as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||