Tumbling Mill (Power, Morrell Continuum)

Description

This article describes the Morrell Continuum (Morrell C) method for estimating the power draw of a tumbling mill.

The Morrell C model is a theoretical approach based on the dynamics of the grinding charge. By making simplifying assumptions about the charge shape, composition and position, Morrell developed analytical solutions to equations describing the the rate at which potential and kinetic energy is imparted to the charge during mill rotation.

Model theory

Morrell's Continuum approach expresses power input to the motor of a tumbling mill as:

${\text{Gross power (kW)}}={\text{No-load power}}+(k\times {\text{Charge motion power}})$

where $k$ is a lumped calibration parameter accounting for power losses, found to be a value of 1.26 for industrial mills.

Sub-components of the gross power equation are described below.

Charge motion power

Figure 1. Overflow discharge tumbling mill profile showing Morrell's assumed charge shape and slurry pool level for the Continuum model.

Figure 2. Schematic of a tumbling mill showing key dimensions.

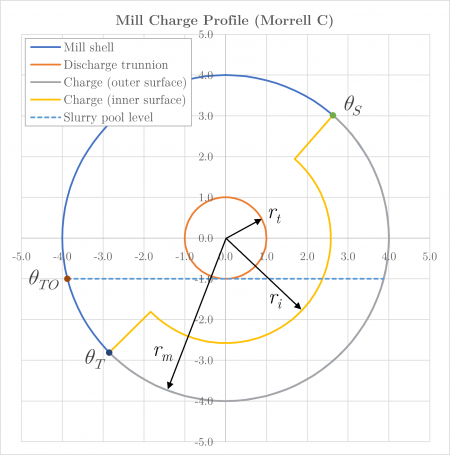
To determine the charge motion power, Morrell adopted the simplified continuum charge shape shown in Figure 1.

Power draw is then developed from a consideration of the rate at which potential and kinetic energy is transferred to the charge and the slurry pool (if present).

The net power imparted to the charge in the cylindrical section of the mill was analytically derived as:

$P_{\rm {t}}={\frac {\pi gLN_{\rm {m}}r_{\rm {m}}}{3\left(r_{\rm {m}}-zr_{i}\right)}}\left[2r_{\rm {m}}^{3}-3zr_{\rm {m}}^{2}+r_{i}^{3}\left(3z-2\right)\right]\times {\big [}\rho _{\rm {c}}\left(\sin \theta _{\rm {S}}-\sin \theta _{\rm {T}}\right)+\rho _{\rm {p}}\left(\sin \theta _{\rm {T}}-\sin \theta _{\rm {TO}}{\big )}\right]+L\rho _{\rm {c}}\left({\frac {N_{\rm {m}}r_{\rm {m}}\pi }{\left(r_{\rm {m}}-zr_{i}\right)}}\right)\left[\left(r_{\rm {m}}-zr_{i}\right)^{4}-r_{i}^{4}\left(z-1\right)^{4}\right]$

and for the cone end section:

$P_{\rm {c}}={\frac {\pi L_{\rm {d}}gN_{\rm {m}}}{3(r_{\rm {m}}-r_{\rm {t}})}}{\bigg \{}\left(r_{\rm {m}}^{4}-4r_{\rm {m}}r_{i}^{3}+3r_{i}^{4}\right){\big [}\rho _{\rm {c}}\left(\sin \theta _{\rm {S}}-\sin \theta _{\rm {T}}\right)+\rho _{\rm {p}}\left(\sin \theta _{\rm {T}}-\sin \theta _{\rm {TO}}\right){\big ]}{\bigg \}}+{\frac {2\pi ^{3}N_{\rm {m}}^{3}L_{\rm {d}}\rho _{\rm {c}}}{5(r_{\rm {m}}-r_{\rm {t}})}}{\big (}r_{\rm {m}}^{5}-5r_{\rm {m}}r_{i}^{4}+4r_{i}^{5}{\big )}$

where:

• $P_{\rm {t}}$ is power draw of the cylindrical section of the mill (kW)
• $P_{\rm {c}}$ is power draw of the two cone ends of the mill (kW)
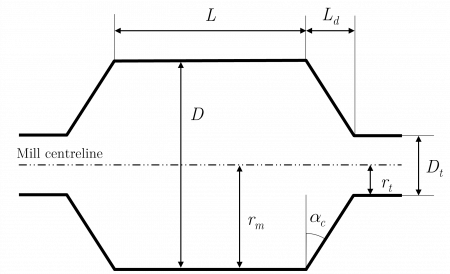
• $L$ is length of the cylindrical section (belly) of the mill inside liners (m)
• $L_{\rm {d}}$ is length of the cone end (m)
• $g$ is acceleration due to gravity (m/s²)
• $N_{\rm {m}}$ is the rotational rate of the mill (rev/s)
• $\rho _{\rm {c}}$ is the density of the total charge (t/m³)
• $\rho _{\rm {p}}$ is the density of discharge pulp (t/m³)
• $r_{\rm {m}}$ is the mill radius inside liners (m)
• $r_{\rm {t}}$ is the trunnion radius inside liners (m)
• $r_{i}$ is the inner charge surface radius (m)
• $\theta _{\rm {S}}$ is the angle of the charge shoulder (radians)
• $\theta _{\rm {T}}$ is the angle of the charge toe (radians)
• $\theta _{\rm {TO}}$ is the angle of the slurry pool surface at the toe (radians)

and all angles are unit circle positive.

The total charge motion power is the sum of the net power imparted to the charge in the cylindrical and cone sections, i.e.

${\text{Charge motion power}}=P_{\rm {t}}+P_{\rm {c}}$

The length of the cone end, $L_{\rm {d}}$ (m), is:

$L_{\rm {d}}=(r_{\rm {m}}-r_{\rm {t}})\tan \alpha _{c}$

where $\alpha _{c}$ is the cone angle, measured as the angular displacement of the cone surface from the vertical direction (rad).

The parameter $z$ is an empirical term that relates the rotational rate of particles at radial positions within the charge to the rotational rate of the mill, and is defined as:

$z=\left(1-J_{\rm {t}}\right)^{0.4532}$

where $J_{\rm {t}}$ is the volumetric fraction of the mill occupied by balls and coarse rock (including void space and interstitial slurry) (v/v).

The remaining parameters of the charge motion power equations are described below.

Charge position

The charge motion power equations require the position of the charge shoulder ($\theta _{\rm {S}}$), charge toe ($\theta _{\rm {T}}$), slurry pool level ($\theta _{\rm {TO}}$, for overflow discharge mills) and the inner charge surface radius ($r_{i}$), in addition to mill dimensions and charge composition.

Morrell developed the following series of relations to estimate the charge geometry.

The position of the toe of the charge, $\theta _{\rm {T}}$ (rad), is defined as:

$\theta _{\rm {T}}=2.5307\left(1.2796-J_{\rm {t}}\right)\left(1-{\rm {e}}^{-19.42(\phi _{\rm {c}}-\phi )}\right)+{\frac {\pi }{2}}$

where $\phi$ (frac) is the theoretical fraction critical speed, and the fraction of critical speed at which centrifuging actually occurs, $\phi _{\rm {c}}$ (frac), is:

$\phi _{\rm {c}}={\begin{cases}\phi &\phi >0.35(3.364-J_{\rm {t}})\\0.35(3.364-J_{\rm {t}})&\phi \leq 0.35(3.364-J_{\rm {t}})\\\end{cases}}$

The position of the shoulder of the charge, $\theta _{\rm {S}}$ (rad), is:

$\theta _{\rm {S}}={\frac {\pi }{2}}-\left(\theta _{\rm {T}}-{\frac {\pi }{2}}\right){\big [}\left(0.336+0.1041\phi \right)+\left(1.54-2.5673\phi \right)J_{\rm {t}}{\big ]}$

The position of the slurry pool level, $\theta _{\rm {TO}}$ (rad), is:

$\theta _{\rm {TO}}={\begin{cases}\theta _{\rm {T}}&{\mbox{for grate discharge mills}}\\\pi +\arcsin \left({\frac {r_{\rm {t}}}{r_{\rm {m}}}}\right)&{\mbox{for overflow discharge mills}}\\\end{cases}}$

where $r_{\rm {t}}$ (m) is the radius of the trunnion.

The inner charge surface radius, $r_{i}$ (m), is:

$r_{i}=r_{\rm {m}}\left(1-{\frac {2\pi \beta J_{\rm {t}}}{2\pi +\theta _{\rm {S}}-\theta _{\rm {T}}}}\right)^{0.5}$

where the fraction of total charge in the active region, $\beta$ (frac), is:

$\beta ={\frac {t_{\rm {c}}}{t_{\rm {f}}+t_{\rm {c}}}}$

The time taken to travel between the toe and shoulder of the charge during one revolution, $t_{\rm {c}}$ (s), is:

$t_{\rm {c}}={\frac {2\pi -\theta _{\rm {T}}+\theta _{\rm {S}}}{2\pi {\bar {N}}}}$

where the mean rotational rate, ${\bar {N}}$ (rev/s), is:

${\bar {N}}\approx {\frac {N_{\rm {m}}}{2}}$

The time taken to travel between the shoulder and toe of the charge in free flight during one revolution, $t_{\rm {f}}$ (s), is:

$t_{\rm {f}}\approx \left({\frac {2{\bar {r}}\left(\sin \theta _{\rm {S}}-\sin \theta _{\rm {T}}\right)}{g}}\right)^{0.5}$

where the mean radial position ${\bar {r}}$ (m), is:

${\bar {r}}={\frac {r_{\rm {m}}}{2}}\left[1+\left(1-{\frac {2\pi J_{\rm {t}}}{2\pi +\theta _{\rm {S}}-\theta _{\rm {T}}}}\right)^{0.5}\right]$

Charge density

The apparent density of the charge, $\rho _{\rm {c}}$, including balls, coarse rocks, voids and slurry, is:

$\rho _{\rm {c}}={\frac {J_{\rm {t}}\rho _{\rm {o}}(1-E+EUS)+J_{\rm {B}}(\rho _{\rm {B}}-\rho _{\rm {o}})(1-E)+J_{\rm {t}}EU(1-S)}{J_{\rm {t}}}}$

where:

• $\rho _{\rm {o}}$ is the density of ore (t/m³)
• $E$ is volumetric fraction of interstitial void space in the charge, typically 0.4 (v/v)
• $U$ is the volumetric fraction of interstitial grinding media voidage occupied by slurry (v/v), $U\leq 1$
• $S$ is the volume fraction of solids in the mill discharge (v/v)
• $J_{\rm {B}}$ is the volumetric fraction of the mill occupied by balls (including voids) (v/v)

No-load power

No-load power is defined as:

${\text{No-load power}}=1.68D^{2.05}\left[\phi (0.667L_{\rm {d}}+L\right]^{0.82}$

where $D$ is mill diameter inside liners (m)

Additional notes

The Morrell C model is only applicable to grate discharge mills that do not exhibit a slurry pool, i.e. $U\leq 1$.

For overflow discharge mills, the slurry pool component is accounted for by the $\theta _{\rm {TO}}$ term, which assumes overflow at the exact height of the trunnion lip.

Excel

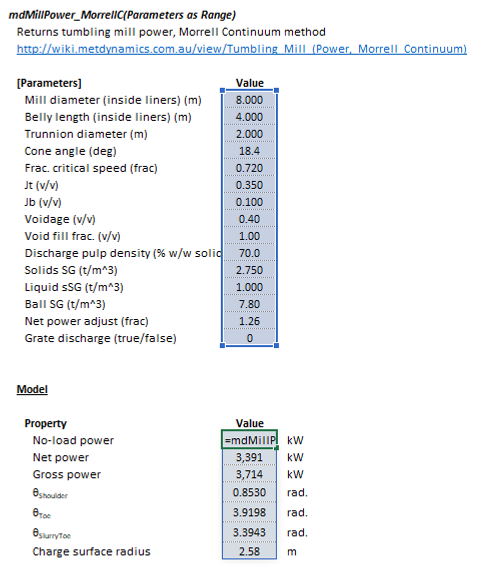
The Morrell Continuum mill power model may be invoked from the Excel formula bar with the following function call:

=mdMillPower_MorrellC(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

$Parameters={\begin{bmatrix}D{\text{ (m)}}\\L{\text{ (m)}}\\D_{\rm {t}}{\text{ (m)}}\\\alpha _{c}{\text{ (degrees)}}\\\phi {\text{ (frac)}}\\J_{\rm {t}}{\text{ (v/v)}}\\J_{\rm {B}}{\text{ (v/v)}}\\E{\text{ (v/v)}}\\U{\text{ (v/v)}}\\{\text{Discharge pulp density (}}\%{\text{ w/w)}}\\\rho _{\rm {o}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\rho _{\rm {L}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\\rho _{\rm {B}}{\text{ (t/m}}^{\text{3}}{\text{)}}\\k{\text{ (kW/kW)}}\\{\text{Grate discharge}}\\\end{bmatrix}},\;\;\;\;\;\;mdMillPower\_MorrellC={\begin{bmatrix}{\text{No-load power (kW)}}\\{\text{Net power (kW)}}\\{\text{Gross power (kW)}}\\\theta _{\rm {S}}{\text{ (rad)}}\\\theta _{\rm {T}}{\text{ (rad)}}\\\theta _{\rm {TO}}{\text{ (rad)}}\\r_{i}{\text{ (m)}}\\\end{bmatrix}}\;\;\;\;\;\;$ where: $D_{\rm {t}}$ is the diameter of the discharge trunnion (m) ${\text{Discharge pulp density}}$ is the mass fraction of solids in the discharge pulp (% w/w) $\rho _{\rm {L}}$ is the density of liquids (t/m3) ${\text{Discharge mechanism}}$ is true if the mill is configured with a grate discharge, false if an overflow discharge ${\text{Net power (kW) = Gross power (kW) - No-load power (kW)}}$

Figure 3. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

SysCAD

The Morrell Continuum power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.

Tag (Long/Short)	Input / Display	Description/Calculated Variables/Options
MorrellC
HelpLink		Opens a link to this page using the system default web browser. Note: Internet access is required.
MillDiameter	Input/Display	Diameter of the mill (inside liners).
BellyLength	Input/Display	Length of the cylindrical section (belly) of the mill (inside liners).
TrunnionDiameter	Input/Display	Diameter of the trunnion (inside liners).
FracCS	Input/Display	Fraction critical speed of the mill.
Jt	Input/Display	Volumetric fraction of the mill occupied by balls and coarse rock (including voids).
Jb	Input/Display	Volumetric fraction of the mill occupied by balls (including voids).
Voidage	Input/Display	Volumetric fraction of interstitial void space in the charge. Usually 0.4.
VoidFillFraction	Input/Display	Volumetric fraction of interstitial grinding media voidage occupied by slurry.
ConeAngle	Input/Display	Angular displacement of the cone surface from the vertical direction.
DischargePulpDensity	Display	Mass fraction of solids in discharge slurry.
SolidsSG	Display	Specific Gravity or density of solids.
LiquidsSG	Display	Specific Gravity or density of liquids.
BallSG	Input/Display	Specific Gravity or density of balls.
DischargeType	Grate/Overflow	Discharge configuration, grate or overflow.
NetPowerAdjust	Input	Lumped calibration parameter accounting for power losses. Found to be a value of 1.26 for industrial mills.
ThetaShoulder	Display	Angle of the charge shoulder.
ThetaToe	Display	Angle of the charge toe.
ThetaSlurryToe	Display	Angle of the slurry pool surface at the toe.
ChargeSurfaceRadius	Display	Radius of the inner surface of the charge.
NoLoadPower	Display	Power input to the motor when the mill is empty (no balls, rocks or slurry).
NetPower	Display	Charge motion power, including losses.
GrossPower	Display	Power input to the motor.

See also

• Morrell Empirical method