Tumbling Mill (Slurry Flow)

Description

This article describes the Morrell and Stephenson (1996) method for estimating the volumetric flow rate of slurry discharged from a grate discharge tumbling mill.

Model theory

Morrell and Stephenson (1996) suggest the total discharge flow rate of liquids plus solids of size less than $x_{\rm {m}}$ (which act like water) is the combination of discharge through the grinding media zone and slurry pool (if present):

${\begin{array}{ll}Q_{\rm {m}}=k_{\rm {m}}{J_{\rm {pm}}}^{2}\gamma ^{2.5}A\phi ^{-1.34}D^{0.5}&J_{\rm {pm}}\leq J_{\rm {max}}\\Q_{\rm {t}}=k_{\rm {t}}J_{\rm {pt}}\gamma ^{2}AD^{0.5}&J_{\rm {p}}>J_{\rm {max}}\\&J_{\rm {pt}}=J_{\rm {p}}-J_{\rm {max}}\\&J_{\rm {max}}=0.5J_{\rm {t}}-J_{\rm {po}}\\&J_{\rm {po}}=0.33(1-r_{\rm {n}})\\&J_{\rm {p}}=J_{\rm {pg}}-J_{\rm {po}}\\\end{array}}$

where

• $Q_{\rm {m}}$ and $Q_{\rm {t}}$ are the volumetric discharge rates of slurry through the grinding media zone and slurry pool, respectively (m³/h)
• $k_{\rm {m}}$ and $k_{\rm {t}}$ are the slurry discharge coefficients for the grinding media zone and slurry pool, respectively
• $J_{\rm {pm}}$ is the net fractional slurry hold-up in the grinding media interstices (v/v)
• $J_{\rm {pt}}$ is the net fractional slurry hold-up in the slurry pool (v/v)
• $\gamma$ is the open area weighted mean radial position of the grate apertures (m/m)
• $A$ is the total open area of grate apertures (m²)
• $D$ is the mill diameter (m)
• $\phi$ is the fraction critical speed of the mill (frac)
• $J_{\rm {p}}$ is the net fraction of mill volume occupied by slurry (v/v)
• $J_{\rm {max}}$ is the maximum net fractional slurry hold-up in the grinding media zone (v/v)
• $J_{\rm {t}}$ is the fraction of mill volume occupied by grinding media, including associated interstices (v/v)
• $J_{\rm {po}}$ is the dead fraction of mill volume which is occupied by slurry before discharge commences (v/v)
• $J_{\rm {pg}}$ is gross fraction of mill volume occupied by slurry (v/v)
• $r_{\rm {n}}$ is the relative radial position of the outermost grate apertures (m/m)

The mean radial position of the grate apertures, $\gamma$, is defined as:

$\gamma ={\frac {\sum {r_{i}a_{i}}}{r_{\rm {m}}\sum {a_{i}}}}$

where:

• $a_{i}$ is the open area of all holes (m²) at radial position $r_{i}$ (m)
• $r_{\rm {m}}$ is the radius of the mill inside the liners (m)

In addition, solids greater than $x_{\rm {m}}$ but less than the grate aperture size will also discharge from the mill. To estimate total discharge flow rate, $Q$ (m³/h), Morrell and Stephenson (1996) suggest the following correction:

$Q=k_{\rm {g}}(Q_{\rm {m}}+Q_{\rm {t}})$

where $k_{\rm {g}}$ is a factor to account for coarse material, typically taking the values shown in Table 1.

Table 1. Recommended values for $k_{\rm {g}}$.

Aperture	$k_{\rm {g}}$
Grates only; <19mm	1.05 - 1.1
Grates only; 19mm - 28mm	1.1 1.15
Grates >38mm or pebble ports	1.15 - 1.25
Pebble port open area > Grate open area	1.25

Excel

The Morrell and Stephenson grate discharge mill slurry flow model may be invoked from the Excel formula bar with the following function call:

=mdMillSlurryFlow_MorrellStephenson(Parameters as Range)

Invoking the function with no arguments will print Help text associated with the model, including a link to this page.

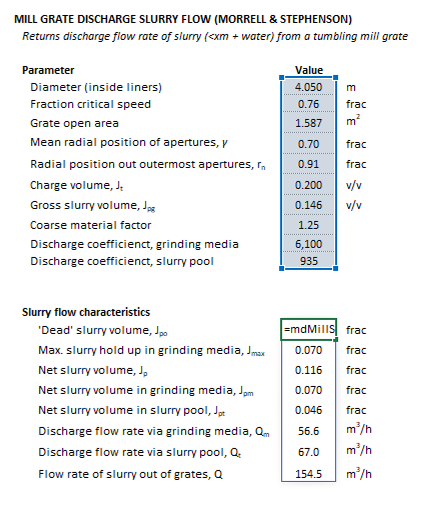
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:

$Parameters={\begin{bmatrix}D{\text{ (m)}}\\\phi {\text{ (frac)}}\\A{\text{ (m}}^{\text{2}}{\text{)}}\\\gamma {\text{ (m/m)}}\\r_{\rm {n}}{\text{ (m/m)}}\\J_{\rm {t}}{\text{ (v/v)}}\\J_{\rm {pg}}{\text{ (v/v)}}\\k_{\rm {g}}\\k_{\rm {m}}\\k_{\rm {t}}\\\end{bmatrix}},\;\;\;\;\;\;mdMillSlurryFlow\_MorrellStephenson={\begin{bmatrix}J_{\rm {po}}{\text{ (v/v)}}\\J_{\rm {max}}{\text{ (v/v)}}\\J_{p}{\text{ (v/v)}}\\J_{\rm {pm}}{\text{ (v/v)}}\\J_{\rm {pt}}{\text{ (v/v)}}\\Q_{\text{m}}{\text{ (m}}^{\text{3}}{\text{/h)}}\\Q_{\rm {t}}{\text{ (m}}^{\text{3}}{\text{/h)}}\\Q{\text{ (m}}^{\text{3}}{\text{/h)}}\\\end{bmatrix}}\;\;\;\;\;\;$

Figure 1. Example showing the selection of the Parameters (blue frame), and Results (light blue frame) arrays in Excel.

See also

• Dynamic Perfect Mixing ball mill model
• AG/SAG Mill (Variable Rates)
• AG/SAG Mill (Variable Rates, Dynamic)