Tumbling Mill (Power, Morrell Continuum): Difference between revisions
md>Scott.Munro m (→Excel) |
imported>Scott.Munro m (→Description) |
||
| (8 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
This article describes the '''Morrell Continuum''' (Morrell C) method for estimating the power draw of a tumbling mill.{{Morrell_(1996a)}} | This article describes the '''Morrell Continuum''' (Morrell C) method for estimating the power draw of a tumbling mill.{{Morrell_(1996a)}} | ||
The Morrell C model is a theoretical approach based on the dynamics of the grinding charge. By making simplifying assumptions about the charge shape, composition and position, Morrell developed analytical solutions to equations describing | The Morrell C model is a theoretical approach based on the dynamics of the grinding charge. By making simplifying assumptions about the charge shape, composition and position, Morrell developed analytical solutions to equations describing the rate at which potential and kinetic energy is imparted to the charge during mill rotation. | ||
== Model theory == | == Model theory == | ||
Morrell's Continuum approach expresses power input to the motor of a tumbling mill as: | {{Restricted content}} | ||
<hide> | |||
Morrell's Continuum approach expresses power input to the motor of a tumbling mill as:{{Morrell (1996a)}} | |||
:<math>\text{Gross power (kW)} = \text{No-load power} + (k \times \text{Charge motion power})</math> | :<math>\text{Gross power (kW)} = \text{No-load power} + (k \times \text{Charge motion power})</math> | ||
| Line 27: | Line 30: | ||
The net power imparted to the charge in the cylindrical section of the mill was analytically derived as: | The net power imparted to the charge in the cylindrical section of the mill was analytically derived as: | ||
:<math> | :<math>P_{\rm t} = \frac{\pi g L N_{\rm m} r_{\rm m}}{3 \left (r_{\rm m} - zr_{\rm i} \right )} \left [ 2r_{\rm m}^3 - 3zr_{\rm m}^2 + r_{\rm i}^3 \left (3z - 2 \right ) \right ] \times \big [ \rho_{\rm c} \left ( \sin \theta_{\rm S} - \sin \theta_{\rm T} \right ) + \rho_{\rm p} \left ( \sin \theta_{\rm T} - \sin \theta_{\rm TO} \big ) \right ] + L \rho_{\rm c} \left ( \frac{N_{\rm m}r_{\rm m} \pi}{\left ( r_{\rm m} - zr_{\rm i} \right)} \right ) \left [ \left( r_{\rm m} - zr_{\rm i} \right )^4 - r_{\rm i}^4 \left (z - 1 \right )^4 \right ] </math> | ||
and for the cone end section: | and for the cone end section: | ||
:<math> | :<math>P_{\rm c} = \frac{\pi L_{\rm d} g N_{\rm m}}{3(r_{\rm m} - r_{\rm t})} \bigg \{ \left ( r_{\rm m}^4 - 4r_{\rm m}r_{\rm i}^3 + 3r_{\rm i}^4 \right ) \big[ \rho_{\rm c} \left ( \sin \theta_{\rm S} - \sin \theta_{\rm T} \right ) + \rho_{\rm p} \left ( \sin \theta_{\rm T} - \sin \theta_{\rm TO} \right ) \big] \bigg \} + \frac{2 \pi^3 N_{\rm m}^3 L_{\rm d} \rho_{\rm c}}{5(r_{\rm m} - r_{\rm t})} \big ( r_{\rm m}^5 - 5r_{\rm m}r_{\rm i}^4 + 4r_{\rm i}^5 \big )</math> | ||
where: | where: | ||
* <math> | * <math>P_{\rm t}</math> is power draw of the cylindrical section of the mill (kW) | ||
* <math> | * <math>P_{\rm c}</math> is power draw of the two cone ends of the mill (kW) | ||
* <math>L</math> is length of the cylindrical section (belly) of the mill inside liners (m) | * <math>L</math> is length of the cylindrical section (belly) of the mill inside liners (m) | ||
* <math> | * <math>L_{\rm d}</math> is length of the cone end (m) | ||
* <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>) | * <math>g</math> is acceleration due to gravity (m/s<sup>2</sup>) | ||
* <math> | * <math>N_{\rm m}</math> is the rotational rate of the mill (rev/s) | ||
* <math>\ | * <math>\rho_{\rm c}</math> is the density of the total charge (t/m<sup>3</sup>) | ||
* <math>\ | * <math>\rho_{\rm p}</math> is the density of discharge pulp (t/m<sup>3</sup>) | ||
* <math> | * <math>r_{\rm m}</math> is the mill radius inside liners (m) | ||
* <math> | * <math>r_{\rm t}</math> is the trunnion radius inside liners (m) | ||
* <math> | * <math>r_{\rm i}</math> is the inner charge surface radius (m) | ||
* <math>\ | * <math>\theta_{\rm S}</math> is the angle of the charge shoulder (radians) | ||
* <math>\ | * <math>\theta_{\rm T}</math> is the angle of the charge toe (radians) | ||
* <math>\theta_{TO}</math> is the angle of the slurry pool surface at the toe (radians) | * <math>\theta_{\rm TO}</math> is the angle of the slurry pool surface at the toe (radians) | ||
and all angles are unit circle positive. | and all angles are unit circle positive. | ||
| Line 53: | Line 56: | ||
The total charge motion power is the sum of the net power imparted to the charge in the cylindrical and cone sections, i.e. | The total charge motion power is the sum of the net power imparted to the charge in the cylindrical and cone sections, i.e. | ||
:<math>\text{Charge motion power} = | :<math>\text{Charge motion power} = P_{\rm t} + P_{\rm c}</math> | ||
The length of the cone end, <math> | The length of the cone end, <math>L_{\rm d}</math> (m), is: | ||
:<math> | :<math>L_{\rm d} = (r_{\rm m} - r_{\rm t}) \tan \alpha_{c}</math> | ||
where <math>\alpha_{c}</math> is the cone angle, measured as the angular displacement of the cone surface from the vertical direction (rad). | where <math>\alpha_{c}</math> is the cone angle, measured as the angular displacement of the cone surface from the vertical direction (rad). | ||
| Line 63: | Line 66: | ||
The parameter <math>z</math> is an empirical term that relates the rotational rate of particles at radial positions within the charge to the rotational rate of the mill, and is defined as: | The parameter <math>z</math> is an empirical term that relates the rotational rate of particles at radial positions within the charge to the rotational rate of the mill, and is defined as: | ||
:<math>z = \left ( 1 - | :<math>z = \left ( 1 - J_{\rm t} \right )^{0.4532}</math> | ||
where <math> | where <math>J_{\rm t}</math> is the volumetric fraction of the mill occupied by balls and coarse rock (including void space and interstitial slurry) (v/v). | ||
The remaining parameters of the charge motion power equations are described below. | The remaining parameters of the charge motion power equations are described below. | ||
| Line 71: | Line 74: | ||
=== Charge position === | === Charge position === | ||
The charge motion power equations require the position of the charge shoulder (<math>\ | The charge motion power equations require the position of the charge shoulder (<math>\theta_{\rm S}</math>), charge toe (<math>\theta_{\rm T}</math>), slurry pool level (<math>\theta_{\rm TO}</math>, for overflow discharge mills) and the inner charge surface radius (<math>r_{\rm i}</math>), in addition to mill dimensions and charge composition. | ||
Morrell developed the following series of relations to estimate the charge geometry. | Morrell developed the following series of relations to estimate the charge geometry.{{Morrell (1996a)}} | ||
The position of the '''toe''' of the charge, <math>\ | The position of the '''toe''' of the charge, <math>\theta_{\rm T}</math> (rad), is defined as: | ||
:<math>\ | :<math>\theta_{\rm T} = 2.5307 \left ( 1.2796 - J_{\rm t} \right ) \left (1 - {\rm e}^{-19.42(\phi_{\rm c} - \phi)} \right ) + \frac{\pi}{2}</math> | ||
where <math>\phi</math> (frac) is the theoretical [[Tumbling Mill (Speed)|fraction critical speed]], and the fraction of critical speed at which centrifuging actually occurs, <math>\ | where <math>\phi</math> (frac) is the theoretical [[Tumbling Mill (Speed)|fraction critical speed]], and the fraction of critical speed at which centrifuging actually occurs, <math>\phi_{\rm c}</math> (frac), is: | ||
:<math> \ | :<math> \phi_{\rm c} = | ||
\begin{cases} | \begin{cases} | ||
\phi & \phi>0.35(3.364- | \phi & \phi>0.35(3.364-J_{\rm t})\\ | ||
0.35(3.364- | 0.35(3.364-J_{\rm t})& \phi \leq 0.35(3.364-J_{\rm t})\\ | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
The position of the '''shoulder''' of the charge, <math>\ | The position of the '''shoulder''' of the charge, <math>\theta_{\rm S}</math> (rad), is: | ||
:<math>\ | :<math>\theta_{\rm S} = \frac{\pi}{2} - \left ( \theta_{\rm T} - \frac{\pi}{2} \right ) \big[ \left ( 0.336 + 0.1041 \phi \right ) + \left (1.54 - 2.5673 \phi \right ) J_{\rm t} \big]</math> | ||
The position of the '''slurry pool''' level, <math>\theta_{TO}</math> (rad), is: | The position of the '''slurry pool''' level, <math>\theta_{\rm TO}</math> (rad), is: | ||
:<math> \theta_{TO} = | :<math> \theta_{\rm TO} = | ||
\begin{cases} | \begin{cases} | ||
\theta_{T} & \mbox{for grate discharge mills}\\ | \theta_{\rm T} & \mbox{for grate discharge mills}\\ | ||
\pi + \arcsin \left ( \frac{ | \pi + \arcsin \left ( \frac{r_{\rm t}}{r_{\rm m}} \right ) & \mbox{for overflow discharge mills}\\ | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
where <math> | where <math>r_{\rm t}</math> (m) is the radius of the trunnion. | ||
The inner '''charge surface radius''', <math> | The inner '''charge surface radius''', <math>r_{\rm i}</math> (m), is: | ||
:<math> | :<math>r_{\rm i} = r_{\rm m} \left ( 1 - \frac{2 \pi \beta J_{\rm t}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}} \right )^{0.5}</math> | ||
where the fraction of total charge in the active region, <math>\beta</math> (frac), is: | where the fraction of total charge in the active region, <math>\beta</math> (frac), is: | ||
:<math>\beta = \frac{ | :<math>\beta = \frac{t_{\rm c}}{t_{\rm f} + t_{\rm c}}</math> | ||
The time taken to travel between the toe and shoulder of the charge during one revolution, <math> | The time taken to travel between the toe and shoulder of the charge during one revolution, <math>t_{\rm c}</math> (s), is: | ||
:<math> | :<math>t_{\rm c} = \frac{2 \pi - \theta_{\rm T} + \theta_{\rm S}}{2 \pi \bar N}</math> | ||
where the mean rotational rate, <math>\bar N</math> (rev/s), is: | where the mean rotational rate, <math>\bar N</math> (rev/s), is: | ||
:<math>\bar N \approx \frac{ | :<math>\bar N \approx \frac{N_{\rm m}}{2}</math> | ||
The time taken to travel between the shoulder and toe of the charge in free flight during one revolution, <math> | The time taken to travel between the shoulder and toe of the charge in free flight during one revolution, <math>t_{\rm f}</math> (s), is: | ||
:<math> | :<math>t_{\rm f} \approx \left ( \frac{2 \bar r \left (\sin \theta_{\rm S} - \sin \theta_{\rm T} \right )}{g} \right )^{0.5}</math> | ||
where the mean radial position <math>\bar r</math> (m), is: | where the mean radial position <math>\bar r</math> (m), is: | ||
:<math>\bar r = \frac{ | :<math>\bar r = \frac{r_{\rm m}}{2} \left [ 1 + \left ( 1 - \frac{2 \pi J_{\rm t}}{2 \pi + \theta_{\rm S} - \theta_{\rm T}} \right )^{0.5} \right ]</math> | ||
=== Charge density === | === Charge density === | ||
The apparent density of the charge, <math>\ | The apparent density of the charge, <math>\rho_{\rm c}</math>, including balls, coarse rocks, voids and slurry, is:{{Morrell (1996a)}} | ||
:<math>\ | :<math>\rho_{\rm c} = \frac{J_{\rm t} \rho_{\rm o} (1 - E + EUS) + J_{\rm B}( \rho_{\rm B} - \rho_{\rm o})(1 - E) + J_{\rm t}EU(1 - S)}{J_{\rm t}}</math> | ||
where: | where: | ||
* <math>\ | * <math>\rho_{\rm o}</math> is the density of ore (t/m<sup>3</sup>) | ||
* <math>E</math> is volumetric fraction of interstitial void space in the charge, typically 0.4 (v/v) | * <math>E</math> is volumetric fraction of interstitial void space in the charge, typically 0.4 (v/v) | ||
* <math>U</math> is the volumetric fraction of interstitial grinding media voidage occupied by slurry (v/v), <math>U \leq 1</math> | * <math>U</math> is the volumetric fraction of interstitial grinding media voidage occupied by slurry (v/v), <math>U \leq 1</math> | ||
* <math>S</math> is the volume fraction of solids in the mill discharge (v/v) | * <math>S</math> is the volume fraction of solids in the mill discharge (v/v) | ||
* <math> | * <math>J_{\rm B}</math> is the volumetric fraction of the mill occupied by balls (including voids) (v/v) | ||
=== No-load power === | === No-load power === | ||
| Line 143: | Line 146: | ||
No-load power is defined as: | No-load power is defined as: | ||
:<math>\text{No-load power} = 1.68D^{2.05} \left [\phi (0. | :<math>\text{No-load power} = 1.68D^{2.05} \left [\phi (0.667L_{\rm d}+L \right ]^{0.82}</math> | ||
where <math>D</math> is mill diameter inside liners (m) | where <math>D</math> is mill diameter inside liners (m) | ||
== Additional notes== | === Additional notes === | ||
The Morrell C model is only applicable to grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>. | The Morrell C model is only applicable to grate discharge mills that do not exhibit a slurry pool, i.e. <math>U \leq 1</math>. | ||
For overflow discharge mills, the slurry pool component is accounted for by the <math>\theta_{TO}</math> term, which assumes overflow at the exact height of the trunnion lip. | For overflow discharge mills, the slurry pool component is accounted for by the <math>\theta_{\rm TO}</math> term, which assumes overflow at the exact height of the trunnion lip. | ||
</hide> | |||
== Excel == | == Excel == | ||
| Line 170: | Line 174: | ||
D\text{ (m)}\\ | D\text{ (m)}\\ | ||
L\text{ (m)}\\ | L\text{ (m)}\\ | ||
D_{\rm t}\text{ (m)}\\ | |||
\alpha_{c}\text{ (degrees)}\\ | \alpha_{c}\text{ (degrees)}\\ | ||
\phi\text{ (frac)}\\ | \phi\text{ (frac)}\\ | ||
J_{\rm t}\text{ (v/v)}\\ | |||
J_{\rm B}\text{ (v/v)}\\ | |||
E\text{ (v/v)}\\ | E\text{ (v/v)}\\ | ||
U\text{ (v/v)}\\ | U\text{ (v/v)}\\ | ||
\text{Discharge pulp density (}\% \text{ w/w)}\\ | \text{Discharge pulp density (}\% \text{ w/w)}\\ | ||
\ | \rho_{\rm o}\text{ (t/m}^{\text{3}}\text{)}\\ | ||
\ | \rho_{\rm L}\text{ (t/m}^{\text{3}}\text{)}\\ | ||
\ | \rho_{\rm B}\text{ (t/m}^{\text{3}}\text{)}\\ | ||
k\text{ (kW/kW)}\\ | k\text{ (kW/kW)}\\ | ||
\text{Grate discharge}\\ | \text{Grate discharge}\\ | ||
| Line 190: | Line 194: | ||
\text{Net power (kW)}\\ | \text{Net power (kW)}\\ | ||
\text{Gross power (kW)}\\ | \text{Gross power (kW)}\\ | ||
\theta_{ | \theta_{\rm S} \text{ (rad)}\\ | ||
\theta_{ | \theta_{\rm T} \text{ (rad)}\\ | ||
\theta_{ | \theta_{\rm TO} \text{ (rad)}\\ | ||
r_{\rm i}\text{ (m)}\\ | |||
\end{bmatrix}\;\;\;\;\;\; | \end{bmatrix}\;\;\;\;\;\; | ||
</math> | </math> | ||
| Line 199: | Line 203: | ||
where: | where: | ||
* <math> | * <math>D_{\rm t}</math> is the diameter of the discharge trunnion (m) | ||
* <math>\text{Discharge pulp density}</math> is the mass fraction of solids in the discharge pulp (% w/w) | * <math>\text{Discharge pulp density}</math> is the mass fraction of solids in the discharge pulp (% w/w) | ||
* <math>\ | * <math>\rho_{\rm L}</math> is the density of liquids (t/m<sup>3</sup>) | ||
* <math>\text{Discharge mechanism}</math> is ''true'' if the mill is configured with a grate discharge, ''false'' if an overflow discharge | * <math>\text{Discharge mechanism}</math> is ''true'' if the mill is configured with a grate discharge, ''false'' if an overflow discharge | ||
* <math>\text{Net power (kW) = Gross power (kW) - No-load power (kW)}</math> | |||
| Line 212: | Line 217: | ||
The Morrell Continuum power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown. | The Morrell Continuum power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown. | ||
{{ | {{SysCAD (Text, Table Header)}} | ||
|- | |- | ||
! colspan="3" style="text-align:left;" |''MorrellC'' | ! colspan="3" style="text-align:left;" |''MorrellC'' | ||
{{SysCAD (Text, Help Link)}} | |||
|- | |- | ||
|MillDiameter | |MillDiameter | ||
| Line 298: | Line 307: | ||
|NetPower | |NetPower | ||
|style="background: #eaecf0" | Display | |style="background: #eaecf0" | Display | ||
|Charge motion power, | |Charge motion power, including losses. | ||
|- | |- | ||
|GrossPower | |GrossPower | ||
Latest revision as of 08:16, 1 May 2025
Description
This article describes the Morrell Continuum (Morrell C) method for estimating the power draw of a tumbling mill.[1]
The Morrell C model is a theoretical approach based on the dynamics of the grinding charge. By making simplifying assumptions about the charge shape, composition and position, Morrell developed analytical solutions to equations describing the rate at which potential and kinetic energy is imparted to the charge during mill rotation.
Model theory
Excel
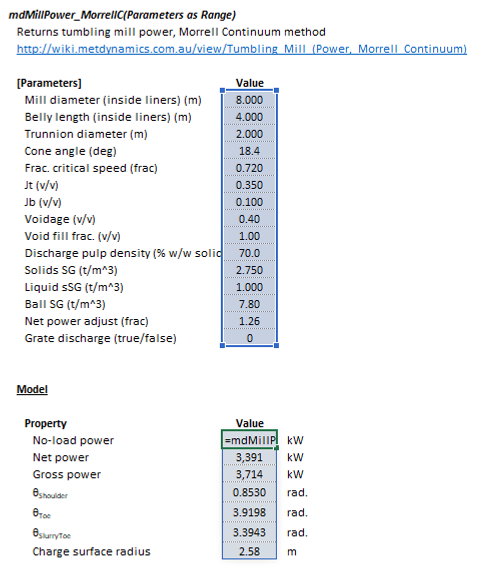
The Morrell Continuum mill power model may be invoked from the Excel formula bar with the following function call:
=mdMillPower_MorrellC(Parameters as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:
|
SysCAD
The Morrell Continuum power model is an optional calculation for tumbling mill units. If selected, the input and display parameters below are shown.
See also
References
- ↑ Morrell, S., 1996. Power draw of wet tumbling mills and its relationship to charge dynamics. Pt. 1: a continuum approach to mathematical modelling of mill power draw. Transactions of the Institution of Mining and Metallurgy. Section C. Mineral Processing and Extractive Metallurgy, 105.