Conversions: Difference between revisions
imported>Scott.Munro |
imported>Scott.Munro |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
This article describes methods for converting: | This article describes methods for converting: | ||
* | * Quantity or fraction retained to cumulative quantity or fraction passing particle size distributions | ||
* Cumulative | * Cumulative quantity passing to quantity retained particle size distributions | ||
* Particle size distributions between different mesh series | * Particle size distributions between different mesh series | ||
* Particle size distribution mesh interval sizes to geometric mean sizes | * Particle size distribution mesh interval sizes to geometric mean sizes | ||
| Line 10: | Line 10: | ||
== Model theory == | == Model theory == | ||
{{ | === Retained to cumulative passing === | ||
A distribution of ''quantity'' retained on a mesh series is converted to a cumulative quantity passing the same series by the following relation: | |||
:<math>P_i = \sum_{j=1}^n p_j - \sum_{k=1}^i p_k \;\;\;\; \text{ for }i=1,\dots, n</math> | |||
where: | |||
* <math>n</math> is the number of size intervals | |||
* <math>i</math> is the index of the size interval, <math>i = \{1,2,\dots,n\}</math> | |||
* <math>P_i</math> is the cumulative quantity passing size interval <math>i</math> | |||
* <math>p_i</math> is the quantity retained on size interval <math>i</math> | |||
Similarly, a cumulative distribution of ''fraction'' passing a mesh series may be obtained from quantity retained data by: | |||
:<math>(P_{\rm n})_i = 1.0 - \dfrac{\sum_{k=1}^i p_k}{\sum_{j=1}^n p_j} \;\;\;\; \text{ for }i=1,\dots, n</math> | |||
where <math>(P_{\rm n})_i</math> is the normalised cumulative quantity passing size interval <math>i</math>. | |||
=== Cumulative passing to retained === | |||
A cumulative ''quantity'' passing distribution is converted to a quantity retained distribution by the following relation: | |||
:<math>p_i = | |||
\begin{cases} | |||
\sum\limits_{j=1}^n p_j - P_i & i = 1\\ | |||
P_{i-1} - P_i & 1 < i \leq n | |||
\end{cases} | |||
</math> | |||
where: | |||
* <math>n</math> is the number of size intervals | |||
* <math>i</math> is the index of the size interval, <math>i = \{1,2,\dots,n\}</math> | |||
* <math>P_i</math> is the cumulative quantity passing size interval <math>i</math> | |||
* <math>p_i</math> is the quantity retained on size interval <math>i</math> | |||
Similarly, a ''fraction'' retained distribution may be obtained from cumulative quantity passing data by: | |||
:<math>(p_{\rm n})_i = | |||
\begin{cases} | |||
1.0 - \dfrac{P_i}{\sum\limits_{j=1}^n p_j} & i = 1\\ | |||
\dfrac{P_{i-1} - P_i}{\sum\limits_{j=1}^n p_j} & 1 < i \leq n | |||
\end{cases} | |||
</math> | |||
where <math>(p_{\rm n})_i</math> is the normalised quantity (i.e. fraction) retained on size interval <math>i</math>. | |||
=== Convert between meshes === | |||
Given a discrete quantity retained distribution <math>(p_1)_i</math> on size interval series <math>(d_1)_i</math>, where <math>i=1,\dots,n</math> and <math>n</math> is the number of size intervals of distribution 1, the quantity retained distribution <math>(p_2)_j</math> on size interval series <math>(d_2)_j</math>, where <math>j=1,\dots,m</math> and <math>m</math> is the number of size intervals of distribution 2, can be obtained from the following procedure: | |||
# Convert quantity retained distribution <math>(p_1)_i</math> to cumulative quantity passing distribution <math>(P_1)_i</math> | |||
# Compute the cumulative quantity passing distribution <math>(P_2)_j</math> on size interval series <math>(d_2)_j</math> using an interpolation method with <math>(P_1)_i</math> and <math>(d_1)_i</math> | |||
# Convert cumulative quantity passing distribution <math>(P_2)_j</math> back to the quantity retained distribution <math>(p_2)_j</math> | |||
Either [[Interpolation#Linear_interpolation|linear interpolation]] or [[Interpolation#Cubic_spline_interpolation|cubic spline interpolation]] methods may be applied to the above procedure. | |||
Furthermore, both the size intervals (<math>d_1</math>, <math>d_2</math>) and cumulative quantity passing (<math>P_1</math>, <math>P_2</math>) distributions may be converted to logarithmic scales prior to interpolation, should this provide a better quality mesh conversion for a given application. | |||
=== Geometric mean size === | === Geometric mean size === | ||
| Line 32: | Line 87: | ||
* <math>d_i</math> is the diameter of particles retained in a mesh at size interval <math>i</math> (mm) | * <math>d_i</math> is the diameter of particles retained in a mesh at size interval <math>i</math> (mm) | ||
* the value of <math>d_i</math> decreases as <math>i</math> increases, i.e. <math>d_{i}>d_{i+1}</math>, <math>d_1</math> = top size, <math>d_n = 0</math> | * the value of <math>d_i</math> decreases as <math>i</math> increases, i.e. <math>d_{i}>d_{i+1}</math>, <math>d_1</math> = top size, <math>d_n = 0</math> | ||
=== Slurry volume flow to mass flow === | |||
The mass flow rates of solids, <math>(Q_{\rm M})_{\rm S}</math> (t/h), and liquids, <math>(Q_{\rm M})_{\rm L}</math> (t/h), in a stream may be computed from: | |||
* The volumetric flow rate of slurry, <math>Q_{\rm V}</math> (m<sup>3</sup>/h), | |||
* The specific gravity of solids, <math>\rho_{\rm S}</math> (t/m<sup>3</sup>), | |||
* The specific gravity of liquids, <math>\rho_{\rm L}</math> (t/m<sup>3</sup>), and | |||
* The mass fraction of solids, <math>C_{\rm W}</math> (w/w) | |||
with: | |||
:<math>(Q_{\rm M})_{\rm S} = \dfrac{Q_{\rm V}}{\left ( \dfrac{1}{\rho_{\rm S}} + \dfrac{1 - C_{\rm W}}{C_{\rm W} \rho_{\rm L}} \right )}</math> | |||
:<math>(Q_{\rm M})_{\rm L} = Q_{\rm M,S} \left ( \dfrac{1 - C_{\rm W}}{C_{\rm W}} \right )</math> | |||
== Excel == | == Excel == | ||
| Line 39: | Line 108: | ||
The retained to cumulative passing method may be invoked from the Excel formula bar with the following function calls: | The retained to cumulative passing method may be invoked from the Excel formula bar with the following function calls: | ||
<syntaxhighlight lang="vb">=mdConvert_RetToCumPass(Retained as Range, Optional returnAsFraction Bool = false)</syntaxhighlight> | <syntaxhighlight lang="vb">=mdConvert_RetToCumPass(Retained as Range, Optional returnAsFraction as Bool = false)</syntaxhighlight> | ||
{{Excel (Text, Help, No Arguments)}} | {{Excel (Text, Help, No Arguments)}} | ||
| Line 86: | Line 155: | ||
The cumulative passing to retained method may be invoked from the Excel formula bar with the following function calls: | The cumulative passing to retained method may be invoked from the Excel formula bar with the following function calls: | ||
<syntaxhighlight lang="vb">=mdConvert_CumPassToRet(CumPassing as Range)</syntaxhighlight> | <syntaxhighlight lang="vb">=mdConvert_CumPassToRet(CumPassing as Range, Optional totalQuantity as Double)</syntaxhighlight> | ||
{{Excel (Text, Help, No Arguments)}} | {{Excel (Text, Help, No Arguments)}} | ||
| Line 123: | Line 192: | ||
* <math>p</math> is the quantity retained on size interval <math>i</math> (<math>1 \leq i \leq n</math>) | * <math>p</math> is the quantity retained on size interval <math>i</math> (<math>1 \leq i \leq n</math>) | ||
* <math>P</math> is the cumulative quantity passing size interval <math>i</math> | * <math>P</math> is the cumulative quantity passing size interval <math>i</math> | ||
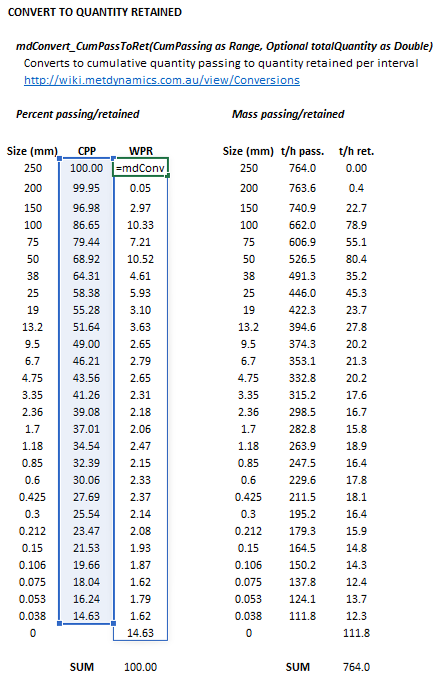
* <math>\mathit{totalQuantity}</math> is an optional value that indicates the total quantity, i.e. the maximum cumulative passing value. | |||
Specifying the <math>\mathit{totalQuantity}</math> may be necessary when the quantity passing the first interval is less than the known total. | |||
For example: | |||
* If the cumulative ''fraction'' passing the first interval is 95%, the <math>\mathit{totalQuantity}</math> should be set to 100%. | |||
* This ensures the quantity retained on the first interval is 5%. | |||
* If <math>\mathit{totalQuantity}</math> were not specified in this case, the quantity retained on the first interval would be 0%, as 95% is otherwise assumed to be the maxmium. | |||
|} | |} | ||
| | | | ||
| Line 148: | Line 225: | ||
\mathit{Size1} & = | \mathit{Size1} & = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
d_1\text{ (mm)}\\ | (d_1)_1\text{ (mm)}\\ | ||
\vdots\\ | \vdots\\ | ||
(d_1)_n\text{ (mm)}\\ | |||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\\ | \\ | ||
\mathit{Dist1} & = | \mathit{Dist1} & = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
p_1\\ | (p_1)_1\\ | ||
\vdots\\ | \vdots\\ | ||
(p_1)_n\\ | |||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\\ | \\ | ||
\mathit{Size2} & = | \mathit{Size2} & = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
(d_2)_1\text{ (mm)}\\ | |||
\vdots\\ | \vdots\\ | ||
(d_2)_m\text{ (mm)}\\ | |||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\\ | \\ | ||
| Line 177: | Line 254: | ||
\mathit{mdConvert\_ToMesh} & = | \mathit{mdConvert\_ToMesh} & = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
(p_2)_1\\ | |||
\vdots\\ | \vdots\\ | ||
(p_2)_m\\ | |||
\end{bmatrix}\\ | \end{bmatrix}\\ | ||
\end{align} | \end{align} | ||
Latest revision as of 05:39, 1 May 2025
Description
This article describes methods for converting:
- Quantity or fraction retained to cumulative quantity or fraction passing particle size distributions
- Cumulative quantity passing to quantity retained particle size distributions
- Particle size distributions between different mesh series
- Particle size distribution mesh interval sizes to geometric mean sizes
- Volumetric flow rates of slurry to mass flow rates of solids and liquids
Model theory
Retained to cumulative passing
A distribution of quantity retained on a mesh series is converted to a cumulative quantity passing the same series by the following relation:
- [math]\displaystyle{ P_i = \sum_{j=1}^n p_j - \sum_{k=1}^i p_k \;\;\;\; \text{ for }i=1,\dots, n }[/math]
where:
- [math]\displaystyle{ n }[/math] is the number of size intervals
- [math]\displaystyle{ i }[/math] is the index of the size interval, [math]\displaystyle{ i = \{1,2,\dots,n\} }[/math]
- [math]\displaystyle{ P_i }[/math] is the cumulative quantity passing size interval [math]\displaystyle{ i }[/math]
- [math]\displaystyle{ p_i }[/math] is the quantity retained on size interval [math]\displaystyle{ i }[/math]
Similarly, a cumulative distribution of fraction passing a mesh series may be obtained from quantity retained data by:
- [math]\displaystyle{ (P_{\rm n})_i = 1.0 - \dfrac{\sum_{k=1}^i p_k}{\sum_{j=1}^n p_j} \;\;\;\; \text{ for }i=1,\dots, n }[/math]
where [math]\displaystyle{ (P_{\rm n})_i }[/math] is the normalised cumulative quantity passing size interval [math]\displaystyle{ i }[/math].
Cumulative passing to retained
A cumulative quantity passing distribution is converted to a quantity retained distribution by the following relation:
- [math]\displaystyle{ p_i = \begin{cases} \sum\limits_{j=1}^n p_j - P_i & i = 1\\ P_{i-1} - P_i & 1 \lt i \leq n \end{cases} }[/math]
where:
- [math]\displaystyle{ n }[/math] is the number of size intervals
- [math]\displaystyle{ i }[/math] is the index of the size interval, [math]\displaystyle{ i = \{1,2,\dots,n\} }[/math]
- [math]\displaystyle{ P_i }[/math] is the cumulative quantity passing size interval [math]\displaystyle{ i }[/math]
- [math]\displaystyle{ p_i }[/math] is the quantity retained on size interval [math]\displaystyle{ i }[/math]
Similarly, a fraction retained distribution may be obtained from cumulative quantity passing data by:
- [math]\displaystyle{ (p_{\rm n})_i = \begin{cases} 1.0 - \dfrac{P_i}{\sum\limits_{j=1}^n p_j} & i = 1\\ \dfrac{P_{i-1} - P_i}{\sum\limits_{j=1}^n p_j} & 1 \lt i \leq n \end{cases} }[/math]
where [math]\displaystyle{ (p_{\rm n})_i }[/math] is the normalised quantity (i.e. fraction) retained on size interval [math]\displaystyle{ i }[/math].
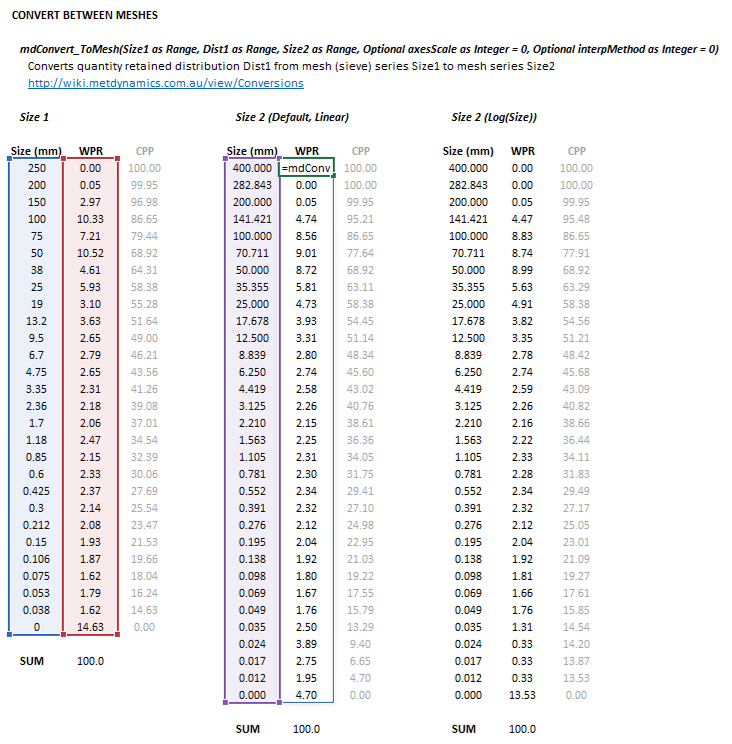
Convert between meshes
Given a discrete quantity retained distribution [math]\displaystyle{ (p_1)_i }[/math] on size interval series [math]\displaystyle{ (d_1)_i }[/math], where [math]\displaystyle{ i=1,\dots,n }[/math] and [math]\displaystyle{ n }[/math] is the number of size intervals of distribution 1, the quantity retained distribution [math]\displaystyle{ (p_2)_j }[/math] on size interval series [math]\displaystyle{ (d_2)_j }[/math], where [math]\displaystyle{ j=1,\dots,m }[/math] and [math]\displaystyle{ m }[/math] is the number of size intervals of distribution 2, can be obtained from the following procedure:
- Convert quantity retained distribution [math]\displaystyle{ (p_1)_i }[/math] to cumulative quantity passing distribution [math]\displaystyle{ (P_1)_i }[/math]
- Compute the cumulative quantity passing distribution [math]\displaystyle{ (P_2)_j }[/math] on size interval series [math]\displaystyle{ (d_2)_j }[/math] using an interpolation method with [math]\displaystyle{ (P_1)_i }[/math] and [math]\displaystyle{ (d_1)_i }[/math]
- Convert cumulative quantity passing distribution [math]\displaystyle{ (P_2)_j }[/math] back to the quantity retained distribution [math]\displaystyle{ (p_2)_j }[/math]
Either linear interpolation or cubic spline interpolation methods may be applied to the above procedure.
Furthermore, both the size intervals ([math]\displaystyle{ d_1 }[/math], [math]\displaystyle{ d_2 }[/math]) and cumulative quantity passing ([math]\displaystyle{ P_1 }[/math], [math]\displaystyle{ P_2 }[/math]) distributions may be converted to logarithmic scales prior to interpolation, should this provide a better quality mesh conversion for a given application.
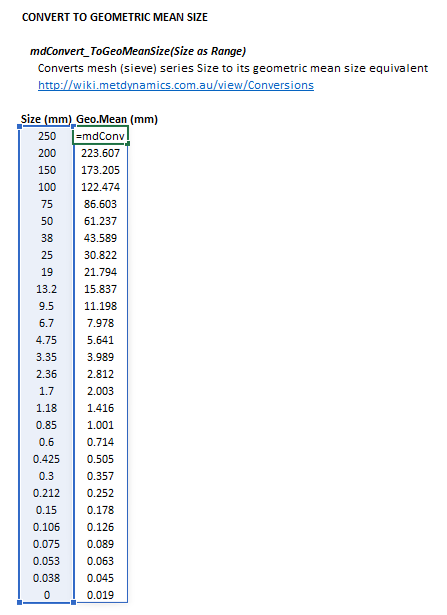
Geometric mean size
The geometric mean size of a particle, [math]\displaystyle{ \bar d_{i} }[/math] (mm), is defined as:
- [math]\displaystyle{ \bar d_{i} = \begin{cases} \sqrt{2} d_1 & i=1\\ \\ \sqrt{d_{i} d_{i-1}} & 1\lt i\lt n\\ \\ 0.5 d_{n-1} & i=n\\ \end{cases} }[/math]
where:
- [math]\displaystyle{ i }[/math] is the index of the size interval, [math]\displaystyle{ i = \{1,2,\dots,n\} }[/math]
- [math]\displaystyle{ n }[/math] is the number of size intervals
- [math]\displaystyle{ d_i }[/math] is the diameter of particles retained in a mesh at size interval [math]\displaystyle{ i }[/math] (mm)
- the value of [math]\displaystyle{ d_i }[/math] decreases as [math]\displaystyle{ i }[/math] increases, i.e. [math]\displaystyle{ d_{i}\gt d_{i+1} }[/math], [math]\displaystyle{ d_1 }[/math] = top size, [math]\displaystyle{ d_n = 0 }[/math]
Slurry volume flow to mass flow
The mass flow rates of solids, [math]\displaystyle{ (Q_{\rm M})_{\rm S} }[/math] (t/h), and liquids, [math]\displaystyle{ (Q_{\rm M})_{\rm L} }[/math] (t/h), in a stream may be computed from:
- The volumetric flow rate of slurry, [math]\displaystyle{ Q_{\rm V} }[/math] (m3/h),
- The specific gravity of solids, [math]\displaystyle{ \rho_{\rm S} }[/math] (t/m3),
- The specific gravity of liquids, [math]\displaystyle{ \rho_{\rm L} }[/math] (t/m3), and
- The mass fraction of solids, [math]\displaystyle{ C_{\rm W} }[/math] (w/w)
with:
- [math]\displaystyle{ (Q_{\rm M})_{\rm S} = \dfrac{Q_{\rm V}}{\left ( \dfrac{1}{\rho_{\rm S}} + \dfrac{1 - C_{\rm W}}{C_{\rm W} \rho_{\rm L}} \right )} }[/math]
- [math]\displaystyle{ (Q_{\rm M})_{\rm L} = Q_{\rm M,S} \left ( \dfrac{1 - C_{\rm W}}{C_{\rm W}} \right ) }[/math]
Excel
Retained to cumulative passing
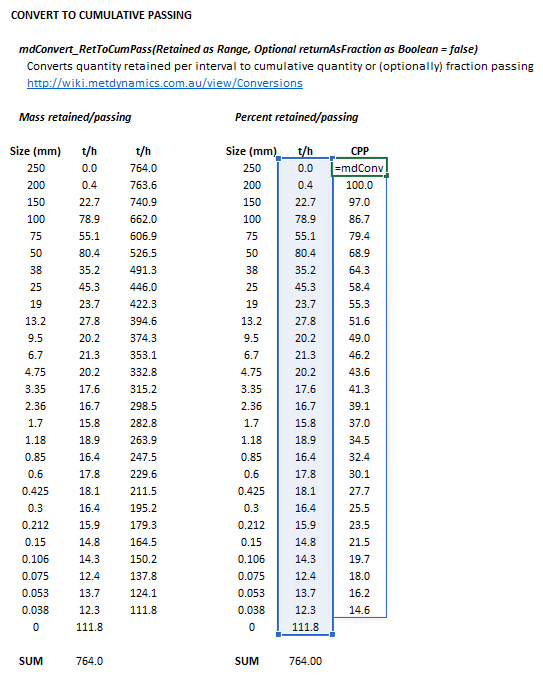
The retained to cumulative passing method may be invoked from the Excel formula bar with the following function calls:
=mdConvert_RetToCumPass(Retained as Range, Optional returnAsFraction as Bool = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Cumulative passing to retained
The cumulative passing to retained method may be invoked from the Excel formula bar with the following function calls:
=mdConvert_CumPassToRet(CumPassing as Range, Optional totalQuantity as Double)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Convert between meshes
The convert between meshes method may be invoked from the Excel formula bar with the following function calls:
=mdConvert_ToMesh(Size1 as Range, Dist1 as Range, Size2 as Range, Optional axesScale as Integer = 0, Optional interpMethod as Integer = 0)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Geometric mean size
The geometric mean size method may be invoked from the Excel formula bar with the following function calls:
=mdConvert_ToGeoMeanSize(Size as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Slurry volume flow to mass flow
The slurry volume flow to mass flow method may be invoked from the Excel formula bar with the following function calls:
=mdConvert_QvToQm(Qv as Double, wtFracSolids as Double, solidsSG as Double, Optional liquidsSG as Double = 1)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||