Comminution Circuit Specific Energy (Morrell): Difference between revisions
md>Scott.Munro mNo edit summary |
imported>Scott.Munro mNo edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
This article describes the '''Morrell''' method for estimating the specific energy of comminution circuits (Morrell et al., 2016).{{Morrell et al. (2016)}} | This article describes the '''Morrell''' method for estimating the specific energy of comminution circuits (Morrell et al., 2016).{{Morrell et al. (2016)}} | ||
The Morrell method estimates the specific energy required to grind ore in comminution circuits, based on empirical models calibrated with laboratory test results. The method integrates ore hardness parameters from standardised testing with proposed circuit grind sizes to compute energy consumption across different equipment types. | |||
== Model theory == | == Model theory == | ||
{{Restricted content}} | |||
<hide> | |||
The Morrell method applies a unified energy-size reduction equation across crushers, tumbling mills, and HPGRs.{{Morrell et al. (2016)}} Each unit’s specific energy is calculated using equipment-specific forms of the equation and ore hardness parameters from standardised ''SMC Test'' and ''Bond Ball Mill Work Index'' tests. | |||
</hide><div class="user-show"> | |||
=== Comminution circuit specific energy === | |||
</div><hide> | |||
The total specific energy, <math>W_{\rm T}</math> (kWh/t), for a full comminution circuit is: | |||
: <math>W_{\rm T} = W_{\rm a} + W_{\rm b} + W_{\rm c} + W_{\rm h} + W_{\rm s}</math> | |||
where: | |||
* <math>W_{\rm a}</math> is the specific energy to grind coarse particles in tumbling mills (kWh/t) | |||
* <math>W_{\rm b}</math> is the specific energy to grind fine particles in tumbling mills (kWh/t) | |||
* <math>W_{\rm c}</math> is the specific energy for conventional crushing (kWh/t) | |||
* <math>W_{\rm h}</math> is the specific energy for High Pressure Grinding Rolls (HPGR) (kWh/t) | |||
* <math>W_{\rm s}</math> is the specific energy correction for size distribution (kWh/t) | |||
Only the terms relevant to the actual circuit configuration are used. Circuit performance is benchmarked by comparing measured total energy to model predictions. | |||
</hide><div class="user-show"> | |||
==== General equation ==== | |||
</div><hide> | |||
All Morrell equations are derived from a general energy-size reduction relationship: | |||
:<math>W = M_{\rm i} \cdot 4 \cdot \left ( x_2^{f(x_2)} - x_1^{f(x_1)} \right )</math> | |||
where: | |||
:<math>f(x) = - \left (0.295 + \dfrac{x}{1{,}000{,}000} \right )</math> | |||
and: | |||
* <math>W</math> is specific energy (kWh/t) | |||
* <math>M_{\rm i}</math> is an ore hardness parameter (e.g., <math>M_{\rm ia}</math>, <math>M_{\rm ib}</math>, <math>M_{\rm ic}</math>, or <math>M_{\rm ih}</math>) | |||
* <math>x_1</math> and <math>x_2</math> are 80% passing feed and product sizes (μm) | |||
</hide><div class="user-show"> | |||
==== Tumbling mills ==== | |||
</div><hide> | |||
These equations apply to AG, SAG, rod, and ball mills performing coarse and fine grinding. | |||
</hide><div class="user-show"> | |||
===== Coarse particle tumbling mill ===== | |||
</div><hide> | |||
The specific energy to grind coarse particles in a tumbling mill (<math>W_{\rm a}</math>) is: | |||
:<math>W_{\rm a} = K_{\rm 1} \cdot M_{\rm ia} \cdot 4 \cdot ({x_2}^{f(x_2)} - {x_1}^{f(x_1)})</math> | |||
where: | |||
* <math>K_{\rm 1}</math> the pebble crusher efficiency factor, set equal to 0.95 for a circuit with pebble crushing, and 1.0 otherwise | |||
* <math>M_{\rm ia}</math> the coarse ore work index (kWh/t) | |||
* <math>x_2 = 750</math>, the nominal transition size between coarse and fine grinding (μm) | |||
* <math>x_1 = F_{80}</math>, the 80% passing size of the feed (μm). | |||
</hide><div class="user-show"> | |||
===== Fine particle tumbling mill ===== | |||
</div><hide> | |||
The specific energy to grind fine particles in a tumbling mill (<math>W_{\rm b}</math>) is: | |||
:<math>W_{\rm b} = M_{\rm ib} \cdot 4 \cdot ({x_3}^{f(x_3)} - {x_2}^{f(x_2)})</math> | |||
where: | |||
* <math>M_{\rm ib}</math> the fine ore work index (kWh/t) | |||
* <math>x_2 = 750</math>, the nominal transition size between coarse and fine grinding (μm) | |||
* <math>x_3 = P_{80}</math>, the 80% passing size of the final grind (μm). | |||
</hide><div class="user-show"> | |||
==== Crushers ==== | |||
</div><hide> | |||
These equations apply to conventional crushing equipment such as jaw, gyratory, and cone crushers. | |||
The specific energy for conventional crushing, <math>W_{\rm c}</math> (kWh/t), is: | |||
: <math>W_{\rm c} = S_{\rm c} \cdot K_{\rm 2} \cdot M_{\rm ic} \cdot 4 \cdot ({x_2}^{f(x_2)} - {x_1}^{f(x_1)})</math> | |||
where: | |||
*<math>K_{\rm 2} = 1.0</math> for crushers operating in closed circuit with a classifying screen, and <math>1.19</math> for open circuit crushing (include AG/SAG pebble crushing). | |||
* <math>M_{\rm ic}</math> the crushing ore work index (kWh/t) | |||
* <math>x_2 = P_{80}</math>, the 80% passing size of the product (μm). | |||
* <math>x_1 = F_{80}</math>, the 80% passing size of the feed (μm). | |||
The coarse ore size scaling factor for crushers, <math>S_{\rm c}</math>, is: | |||
:<math>S_{\rm c} = \min\left(1,\; 55 \cdot (x_1 \cdot x_2)^{-0.2}\right)</math> | |||
</hide><div class="user-show"> | |||
==== High pressure grinding rolls ==== | |||
</div><hide> | |||
These equations apply to High Pressure Grinding Rolls (HPGR) units operating in open or closed circuit. | |||
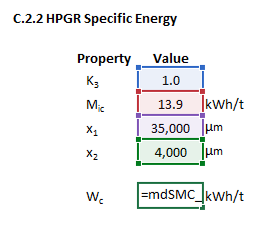
The specific energy for HPGRs (<math>W_{\rm h}</math>) is: | |||
: <math>W_{\rm h} = S_{\rm h} \cdot K_{\rm 3} \cdot M_{\rm ih} \cdot 4 \cdot ({x_2}^{f(x_2)} - {x_1}^{f(x_1)})</math> | |||
where: | |||
*<math>K_{\rm 3} = 1.0</math> for HPGRs in closed circuit with a classifying screen, and <math>1.19</math> for open circuit HPGRs. | |||
* <math>M_{\rm ih}</math> the HPGR ore work index (kWh/t) | |||
* <math>x_2 = P_{80}</math>, the 80% passing size of the product (μm). | |||
* <math>x_1 = F_{80}</math>, the 80% passing size of the feed (μm). | |||
The coarse ore size scaling factor for HPGRs, <math>S_{\rm h}</math>, is: | |||
:<math>S_{\rm h} = \min\left(1,\; 35 \cdot (x_1 \cdot x_2)^{-0.2}\right)</math> | |||
</hide><div class="user-show"> | |||
==== Size distribution correction ==== | |||
</div><hide> | |||
The Morrell method assumes that feed and product size distributions are linear and parallel in log-log space. When this assumption is not valid, typically when a ball mill is fed by a closed-circuit crusher producing a steep size distribution, additional energy is required for grinding. | |||
The size distribution correction factor, <math>W_{\rm s}</math>, accounts for this by adding a penalty to the predicted specific energy. It ensures that circuits with sharper-than-expected feed distributions, which are harder to grind, are correctly assessed for their higher energy demand. | |||
The size distribution specific energy correction (<math>W_{\rm s}</math>) is: | |||
:<math>W_{\rm s} = 0.19 \cdot M_{\rm ia} \cdot 4 \cdot ({x_2}^{f(x_2)} - {x_1}^{f(x_1)})</math> | |||
</hide><div class="user-show"> | |||
=== Hardness parameters === | |||
</div><hide> | |||
The ore hardness parameters <math>M_{\rm ia}</math>, <math>M_{\rm ic}</math>, <math>M_{\rm ih}</math> are derived from the SMC Test. | |||
The fine ore hardness parameter, <math>M_{\rm ib}</math>, is extracted from the results of a standard Bond Ball Work Index test: | |||
{{ | :<math>M_{\rm ib} = \frac{18.18}{{P_{100}}^{0.295} \cdot G_{\rm pb} \cdot \left( {P_{80}}^{f(P_{80})} - {F_{80}}^{f(F_{80})} \right)}</math> | ||
where: | |||
* <math>P_{100}</math> is the closing screen size (μm) | |||
* <math>G_{\rm pb}</math> is the net undersize per revolution (g) | |||
* <math>P_{80}</math>, <math>F_{80}</math> are the product and feed 80% passing sizes, respectively (μm) | |||
</hide><div class="user-show"> | |||
=== Estimating P<sub>80</sub> === | |||
</div><hide> | |||
The [[#General_equation|general energy-size reduction equation]] can be rearranged to solve for the product 80% passing size (<math>P_{\rm 80}</math>), given the specific energy input (<math>W</math>), ore hardness (<math>M_{\rm i}</math>), feed size (<math>F_{\rm 80}</math>), and any applicable scale factor <math>K</math>. | |||
This yields a transcendental equation, as <math>P_{\rm 80}</math> appears both as a base and within the exponent. It cannot be solved analytically and is instead solved numerically using a root-finding algorithm: | |||
:<math>f(x_2) = x_2^{- \left( 0.295 + \dfrac{x_2}{1{,}000{,}000} \right)} - \left( \dfrac{W}{4 M_{\rm i}} + x_1^{- \left( 0.295 + \dfrac{x_1}{1{,}000{,}000} \right)} \right) = 0</math> | |||
This form is useful when specific energy is known and the corresponding product size (<math>P_{\rm 80}</math>) must be estimated, such as in circuit design or performance benchmarking. | |||
</hide><div class="user-show"> | |||
=== Estimating breakage parameters === | |||
</div><hide> | |||
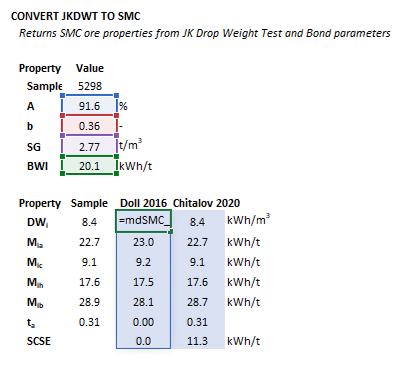
Regression models published by Doll (2016), Doll and Becerra (2017), Lvov and Chitalov (2020), and Chitalov (2021) allow estimation of Morrell comminution parameters from JK Drop Weight Test (JKDWT) ''A'' and ''b'' values, specific gravity (''SG''), and Bond Ball Work Index (''BWI'') results.{{Doll (2016b)}}{{Doll and Becerra (2017)}}{{Lvov and Chitalov (2020a)}}{{Chitalov (2021)}} These models provide an empirical means of estimating SMC parameters where SMC test data is unavailable. | |||
:{| class="wikitable" | |||
|+ Table 1. Regression equations for estimating SMC parameters | |||
! Parameter !! Definition !! Doll (2016-2017) !! Chitalov (2020-2021) | |||
|- | |||
| <math>DWi</math> || Drop Weight Index || <math>91.21 \cdot SG \cdot (A \cdot b)^{-0.97}</math> || <math>92.56 \cdot SG \cdot (A \cdot b)^{-0.977}</math> | |||
|- | |||
| <math>M_{\rm ia}</math> || Coarse ore tumbling mill index || <math>390.87 \cdot (A \cdot b)^{-0.81}</math> || <math>389.97 \cdot (A \cdot b)^{-0.813}</math> | |||
|- | |||
| <math>M_{\rm ib}</math> || Fine ore tumbling mill index || <math>\left( \dfrac{BWI}{1.49} \right)^{\frac{1}{0.78}}</math> || <math>1.86 \cdot BWI - 8.7</math> | |||
|- | |||
| <math>M_{\rm ic}</math> || Crushing index || <math>\dfrac{303.48}{A \cdot b}</math> || <math>303.48 \cdot (A \cdot b)^{-1.003}</math> | |||
|- | |||
| <math>M_{\rm ih}</math> || HPGR index || <math>\dfrac{576.99}{A \cdot b}</math> || <math>576.99 \cdot (A \cdot b)^{-0.999}</math> | |||
|- | |||
| <math>t_{\rm a}</math> || Abrasion index || - || <math>\dfrac{2.6132}{DWi}</math> | |||
|- | |||
| <math>\mathrm{SCSE}</math> || SAG Circuit Specific Energy || - || <math>52.74 \cdot (A \cdot b)^{-0.441}</math> | |||
|} | |||
'''Notes:''' | |||
* <math>A</math> is the maximum t₁₀ value in the JK Drop Weight Test (% passing 1/10 of the original size). It represents the ore's initial response to high-energy impact breakage. | |||
* <math>b</math> is the slope of the breakage curve fitted to <math>t_{10} = A \cdot (1 - e^{-b \cdot E_{\rm cs}})</math>. It describes how quickly the ore approaches its breakage limit as energy increases (dimensionless). | |||
* <math>SG</math> is the specific gravity of the ore (t/m<sup>3</sup>) | |||
* <math>BWI</math> is the Bond Ball Mill Work Index, a measure of ore resistance to fine grinding (kWh/t) | |||
* <math>DWi</math> is the Drop Weight Index, a volumetric hardness measure derived from the JKDWT (kWh/m<sup>3</sup>) | |||
* <math>t_{\rm a}</math> is the abrasion index from the JK Drop Weight Test (%) | |||
* <math>\mathrm{SCSE}</math> is the ''SAG Circuit Specific Energy''. It represents the specific energy predicted for a standard circuit configuration using the ore’s measured A and b parameters. For details, see [https://www.smctesting.com/documents/scse-parameter.pdf SMC Testing - The SCSE Parameter]. | |||
Doll and Becerra (2017) report different regression coefficients for <math>M_{\rm ic}</math> and <math>M_{\rm ih}</math> compared to Doll’s earlier publication (Doll, 2016). Analysis of Doll’s [https://www.sagmilling.com/articles/28/view/?s=1 public grindability database] confirms that the 2017 coefficients are consistent with observed data and are adopted here. | |||
The publications by Lvov and Chitalov (2020) and Chitalov (2021) also report inverted assignments of <math>M_{\rm ic}</math> and <math>M_{\rm ih}</math> in their earlier work. However, the coefficients presented in Chitalov’s 2021 dissertation are numerically identical to those in Doll and Becerra (2017) and are therefore adopted here as well. | |||
</hide> | |||
== Excel == | == Excel == | ||
| Line 347: | Line 537: | ||
\mathit{mdSMC\_AbToSMC} = | \mathit{mdSMC\_AbToSMC} = | ||
\begin{bmatrix} | \begin{bmatrix} | ||
\ | {\rm DW}_{\rm i}\text{ (kWh/m}^3\text{)}\\ | ||
M_{\rm ia}\text{ (kWh/t)}\\ | M_{\rm ia}\text{ (kWh/t)}\\ | ||
M_{\rm ib}\text{ (kWh/t)}\\ | M_{\rm ib}\text{ (kWh/t)}\\ | ||
| Line 353: | Line 543: | ||
M_{\rm ih}\text{ (kWh/t)}\\ | M_{\rm ih}\text{ (kWh/t)}\\ | ||
t_{\rm a}\text{ (-)}\\ | t_{\rm a}\text{ (-)}\\ | ||
\ | {\rm SCSE}\text{ (kWh/t)}\\ | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|- style="vertical-align:top;" | |- style="vertical-align:top;" | ||
| Line 363: | Line 553: | ||
* <math>\mathit{Wi}_{\rm BM}</math> is the Bond Ball Work Index of the ore (kWh/t) | * <math>\mathit{Wi}_{\rm BM}</math> is the Bond Ball Work Index of the ore (kWh/t) | ||
* <math>\mathit{conversionMethod}</math> indicates the correlation set to utilise ''(0 = Doll 2016, 1 = Chitalov 2020)'' | * <math>\mathit{conversionMethod}</math> indicates the correlation set to utilise ''(0 = Doll 2016, 1 = Chitalov 2020)'' | ||
* <math>\ | * <math>{\rm DW}_{\rm i}</math> is the Drop Weight Index (kWh/m<sup>3</sup>) | ||
* <math>M_{\rm ia}</math> is the coarse ore (> 750 μm) work index in tumbling mill circuits (kWh/t) | * <math>M_{\rm ia}</math> is the coarse ore (> 750 μm) work index in tumbling mill circuits (kWh/t) | ||
* <math>M_{\rm ib}</math> is the fine ore (< 750 μm) work index in tumbling mill circuits (kWh/t) | * <math>M_{\rm ib}</math> is the fine ore (< 750 μm) work index in tumbling mill circuits (kWh/t) | ||
| Line 369: | Line 559: | ||
* <math>M_{\rm ih}</math> is the ore work index in HPGR circuits (kWh/t) | * <math>M_{\rm ih}</math> is the ore work index in HPGR circuits (kWh/t) | ||
* <math>t_{\rm a}</math> is the JK Drop Weight Test abrasion breakage parameter | * <math>t_{\rm a}</math> is the JK Drop Weight Test abrasion breakage parameter | ||
* <math>\ | * <math>{\rm SCSE}</math> is the SAG Circuit Specific Energy parameter (kWh/t) | ||
|} | |} | ||
| | | | ||
:[[File:SMC8.png|frame|Figure 8. Example showing the selection of the input parameters (shaded blue, red, purple and green frames), and Results ( | :[[File:SMC8.png|frame|Figure 8. Example showing the selection of the input parameters (shaded blue, red, purple and green frames), and Results (light blue frame) array in Excel.]] | ||
|} | |} | ||
| Line 378: | Line 568: | ||
* [[Comminution Circuit Specific Energy (Bond)]] | * [[Comminution Circuit Specific Energy (Bond)]] | ||
== External links == | |||
* [https://gmggroup.org/the-morrell-method-to-determine-the-efficiency-of-industrial-grinding-circuits/ Global Mining Guidelines Group - The Morrell method for determining comminution circuit specific energy and assessing energy utilization efficiency of existing circuits] | |||
* [https://www.smctesting.com/documents/scse-parameter.pdf SMC Testing - The SCSE Parameter] | |||
* [https://www.smctesting.com/documents/Reporting_JK_Drop_Weight_and_SMC_Test_Results.pdf SMC Testing - Reporting JKDWT and SMC Results] | |||
== References == | == References == | ||
[[Category:Excel]] | [[Category:Excel]] | ||
Latest revision as of 05:59, 11 June 2025
Description
This article describes the Morrell method for estimating the specific energy of comminution circuits (Morrell et al., 2016).[1]
The Morrell method estimates the specific energy required to grind ore in comminution circuits, based on empirical models calibrated with laboratory test results. The method integrates ore hardness parameters from standardised testing with proposed circuit grind sizes to compute energy consumption across different equipment types.
Model theory
Comminution circuit specific energy
General equation
Tumbling mills
Coarse particle tumbling mill
Fine particle tumbling mill
Crushers
High pressure grinding rolls
Size distribution correction
Hardness parameters
Estimating P80
Estimating breakage parameters
Excel
Coarse particle tumbling mill specific energy
The coarse particle tumbling mill specific energy calculation may be invoked from the Excel formula bar with the following function call:
=mdSMC_Wa(K1 as Double, Mia as Double, x1 as Double, Optional returnCalcs as Boolean = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Fine particle tumbling mill specific energy
The fine particle tumbling mill specific energy calculation may be invoked from the Excel formula bar with the following function call:
=mdSMC_Wb(Mib as Double, x3 as Double, Optional returnCalcs as Boolean = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Conventional crushing specific energy
The conventional crushing specific energy calculation may be invoked from the Excel formula bar with the following function call:
=mdSMC_Wc(K2 as Double, Mic as Double, x1 as Double, x2 as Double, Optional returnCalcs as Boolean = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
HPGR specific energy
The HPGR specific energy calculation may be invoked from the Excel formula bar with the following function call:
=mdSMC_Wh(K3 as Double, Mih as Double, x1 as Double, x2 as Double, Optional returnCalcs as Boolean = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Specific energy correction for size distribution
The specific energy correction for size distribution calculation may be invoked from the Excel formula bar with the following function call:
=mdSMC_Ws(Mia as Double, x1 as Double, x2 as Double, Optional returnCalcs as Boolean = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
General comminution specific energy
The general comminution specific energy calculation may be invoked from the Excel formula bar with the following function call:
=mdSMC_W(K as Double, Mi as Double, x1 as Double, x2 as Double, Optional returnCalcs as Boolean = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Calculating P80
The P80 calculation may be invoked from the Excel formula bar with the following function call:
=mdSMC_P80(K as Double, Mi as Double, F80 as Double, W as Double, Optional returnCalcs as Boolean = false)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
Estimating breakage parameters
The breakage parameter estimation may be invoked from the Excel formula bar with the following function call:
=mdSMC_AbToSMC(A as Double, b as Double, SG as Double, BWI as Double, Optional conversionMethod as Integer = 0)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The input parameters and calculation results are defined below in matrix notation, along with an example image showing the selection of the same cells and arrays in the Excel interface:
|
| ||||
See also
External links
- Global Mining Guidelines Group - The Morrell method for determining comminution circuit specific energy and assessing energy utilization efficiency of existing circuits
- SMC Testing - The SCSE Parameter
- SMC Testing - Reporting JKDWT and SMC Results
References
- ↑ Morrell, S., Daniel, M. and Burke, J., 2016. Morrell method for determining comminution circuit specific energy and assessing energy utilization efficiency of existing circuits. Global Mining Standards and Guidelines Group: Ormstown, QC, Canada.
![{\displaystyle {\begin{aligned}K1&={\big [}K_{1}{\big ]}\\{\mathit {Mia}}&={\big [}M_{\rm {ia}}{\text{ (kWh/t)}}{\big ]}\\x1&={\big [}x_{1}{\text{ (}}\mu {\text{m)}}{\big ]}\\{\mathit {returnCalcs}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2100f4f744eff46ff9d35d363a77c200e2616653)











![{\displaystyle {\begin{aligned}{\mathit {Mib}}&={\big [}M_{\rm {ib}}{\text{ (kWh/t)}}{\big ]}\\x3&={\big [}x_{3}{\text{ (}}\mu {\text{m)}}{\big ]}\\{\mathit {returnCalcs}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4b60dc5c3de0dbd9604caf116e413e8361ea633)




![{\displaystyle {\begin{aligned}K2&={\big [}K_{2}{\big ]}\\{\mathit {Mic}}&={\big [}M_{\rm {ic}}{\text{ (kWh/t)}}{\big ]}\\x1&={\big [}x_{1}{\text{ (}}\mu {\text{m)}}{\big ]}\\x2&={\big [}x_{2}{\text{ (}}\mu {\text{m)}}{\big ]}\\{\mathit {returnCalcs}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d69a0378da1e6bc841d1cc9193e4337bd7d40f45)







![{\displaystyle {\begin{aligned}K3&={\big [}K_{3}{\big ]}\\{\mathit {Mih}}&={\big [}M_{\rm {ih}}{\text{ (kWh/t)}}{\big ]}\\x1&={\big [}x_{1}{\text{ (}}\mu {\text{m)}}{\big ]}\\x2&={\big [}x_{2}{\text{ (}}\mu {\text{m)}}{\big ]}\\{\mathit {returnCalcs}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9fa80b4753d10b9c79437011cb9f6fbbe0b027e)





![{\displaystyle {\begin{aligned}{\mathit {Mia}}&={\big [}M_{\rm {ia}}{\text{ (kWh/t)}}{\big ]}\\x1&={\big [}x_{1}{\text{ (}}\mu {\text{m)}}{\big ]}\\x2&={\big [}x_{2}{\text{ (}}\mu {\text{m)}}{\big ]}\\{\mathit {returnCalcs}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eaf9b4d6ce9b2729daee36b15fedc963f6d8b02)


![{\displaystyle {\begin{aligned}K&={\big [}K{\big ]}\\{\mathit {Mi}}&={\big [}M_{\rm {i}}{\text{ (kWh/t)}}{\big ]}\\x1&={\big [}x_{1}{\text{ (}}\mu {\text{m)}}{\big ]}\\x2&={\big [}x_{2}{\text{ (}}\mu {\text{m)}}{\big ]}\\{\mathit {returnCalcs}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9c9433079ff72a48e52c1857ba7cccec261866c)




![{\displaystyle {\begin{aligned}K&={\big [}K{\big ]}\\{\mathit {Mi}}&={\big [}M_{\rm {i}}{\text{ (kWh/t)}}{\big ]}\\F80&={\big [}F_{80}{\text{ (}}\mu {\text{m)}}{\big ]}\\W&={\big [}W{\text{ (kWh/t)}}{\big ]}\\{\mathit {returnCalcs}}&={\big [}({\text{True / False)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6405424c725f31c8bb38f3fbec0ad264fb75bb36)




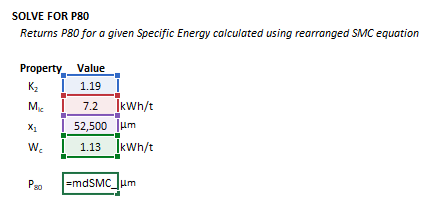
![{\displaystyle {\begin{aligned}A&={\big [}A{\text{ (}}\%{\text{)}}{\big ]}\\b&={\big [}b{\big ]}\\{\mathit {SG}}&={\big [}\rho _{\rm {S}}{\text{ (t/m}}^{3}{\text{)}}{\big ]}\\{\mathit {BWI}}&={\big [}{\mathit {Wi}}_{\rm {BM}}{\text{ (kWh/t}}{\big ]}\\{\mathit {conversionMethod}}&={\big [}{\text{0 (Doll) or 1 (Chitalov)}}{\big ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38bcc1ea873c0bd266c95a4d7cc840970bb8779e)