Comminution Circuit Specific Energy (Bond): Difference between revisions
Scott Munro (talk | contribs) m (1 revision imported) |
imported>Scott.Munro m (Scott.Munro moved page Draft:Comminution Circuit Specific Energy (Bond) to Comminution Circuit Specific Energy (Bond) without leaving a redirect) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Description == | == Description == | ||
This article describes the '''Bond''' method for estimating the specific energy of comminution circuits.{{Rowland (2006)}} | This article describes the '''Bond''' method for estimating the specific energy of rod and ball mill comminution circuits.{{Rowland (2006)}} | ||
== Model theory == | == Model theory == | ||
{{ | The Bond method estimates the specific energy required for comminution based on ore grindability and the extent of size reduction. It is derived from Bond's third theory of comminution, which states that energy consumption is proportional to the reduction in the square root of particle size. The Bond method applies to both rod mills and ball mills. | ||
The specific energy consumption, <math>W</math> (kWh/t), is given by the Bond equation: | |||
:<math>W = 10 \cdot {\rm WI} \left( \frac{1}{\sqrt{P_{80}}} - \frac{1}{\sqrt{F_{80}}} \right)</math> | |||
where: | |||
* <math>{\rm WI}</math> is the Bond Rod Work Index or Bond Ball Work Index, depending on the application (kWh/t) | |||
* <math>F_{80}</math> is the 80% passing size of the feed (μm) | |||
* <math>P_{80}</math> is the 80% passing size of the product (μm) | |||
To correct for variations from the standard test conditions (wet, closed-circuit grinding in a 2.44 m diameter mill), the model includes eight efficiency factors: | |||
:<math>W_{\rm actual} = W \cdot {\rm EF}1 \cdot {\rm EF}2 \cdot {\rm EF}3 \cdot {\rm EF}4 \cdot {\rm EF}5 \cdot {\rm EF}6 \cdot {\rm EF}7 \cdot {\rm EF}8</math> | |||
The correction factors are described below. A conversion factor of ''1 tonne = 1.102 short tonnes'' is applied to work index terms. | |||
The '''dry grinding factor''' (<math>{\rm EF1}</math>) increases the specific energy required for dry grinding compared to wet grinding: | |||
:<math>{\rm EF1} = | |||
\begin{cases} | |||
1.3, & \text{for dry grinding}\\ | |||
1.0, & \text{for wet grinding}\\ | |||
\end{cases} | |||
</math> | |||
The '''open circuit ball mill factor''' (<math>{\rm EF2}</math>) increases the specific energy required for open circuit grinding compared to closed circuit grinding. The factor accounts for the reduced efficiency when no classifier or closing screen is used to control the maximum product size. | |||
The ''control size'' is the hypothetical closing screen size that would be used in an equivalent closed circuit. If the mill is in open circuit, <math>{\rm EF2}</math> is interpolated from the table below based on the percentage of the product passing the control size. For closed-circuit grinding (including all rod mill configurations), <math>{\rm EF2} = 1.0</math>. | |||
:{| class="wikitable" | |||
|+ Table 1. Open-circuit inefficiency factors based on % passing control size (after Rowland, 2006).{{Rowland (2006)}} | |||
! % Passing Control Size !! Inefficiency Multiplier, EF2 | |||
|- | |||
| 50% || 1.035 | |||
|- | |||
| 60% || 1.050 | |||
|- | |||
| 70% || 1.100 | |||
|- | |||
| 80% || 1.200 | |||
|- | |||
| 90% || 1.400 | |||
|- | |||
| 92% || 1.460 | |||
|- | |||
| 95% || 1.570 | |||
|- | |||
| 98% || 1.700 | |||
|} | |||
The '''diameter efficiency factor''' (<math>{\rm EF3}</math>) scales specific energy for mill diameter, <math>D</math> (m): | |||
:<math>{\rm EF3} = | |||
\begin{cases} | |||
\left( \dfrac{2.44}{D} \right)^{0.2}, & D < 3.81 \text{ m}\\ | |||
0.914, & D \geq 3.81 \text{ m}\\ | |||
\end{cases} | |||
</math> | |||
The '''oversized feed factor''' (<math>{\rm EF4}</math>) applies when the mill is to grind a feed that is coarser than an optimum 80% passing feed size, <math>F_{\rm o}</math> (μm): | |||
:<math>{\rm EF4} = | |||
\begin{cases} | |||
\dfrac{R_{\rm r} + \left ( \dfrac{\rm WI}{1.102} - 7 \right ) \cdot \dfrac{F_{80} - F_{\rm o}}{F_{\rm o}}}{R_{\rm r}}, & F_{80} > F_{\rm o}\\ | |||
1.0, & F_{80} \leq F_{\rm o} | |||
\end{cases} | |||
</math> | |||
where: | |||
:<math>F_{\rm o} = | |||
\begin{cases} | |||
16,000 \sqrt \left ( \dfrac{13}{\rm WI} \cdot 1.102 \right ), & \text{ for rod milling}\\ | |||
4,000 \sqrt \left ( \dfrac{13}{\rm WI} \cdot 1.102 \right ), & \text{ for ball milling}\\ | |||
\end{cases} | |||
</math> | |||
and: | |||
:<math>{R_{\rm r}} = \dfrac{F_{80}}{P_{80}}</math> | |||
The '''fineness of grind factor''' (<math>{\rm EF5}</math>) applies when the <math>P_{80}</math> is finer than 75 μm: | |||
:<math>{\rm EF5} = | |||
\begin{cases} | |||
\dfrac{P_{80} + 10.3}{1.145 \, P_{80}}, & P_{80} < 75 \text{ }\mu\text{m}\\ | |||
1.0, & P_{80} \geq 75 \text{ }\mu\text{m}\\ | |||
\end{cases} | |||
</math> | |||
The '''high or low ratio of reduction rod milling factor''' (<math>{\rm EF6}</math>) accounts for reduced efficiency when the reduction ratio in rod milling is too high or too low: | |||
:<math> | |||
\begin{cases} | |||
{\rm EF6} = 1 + \dfrac{(R_{\rm r} - R_{\rm ro})^2}{150}, & \text{if rod milling and } \left |R_{\rm r} - R_{\rm ro} \right | \geq 2 \text{ or } {\rm WI} \geq 7 \cdot 1.102\;\text{ (i.e., 7.714 kWh/t)}\\ | |||
1.0, & \text{otherwise} | |||
\end{cases} | |||
</math> | |||
where: | |||
:<math>R_{\rm ro} = 8 + \dfrac{5L}{D}</math> | |||
and <math>L</math> is rod length (m). | |||
The '''low ratio of reduction ball milling factor''' (<math>{\rm EF7}</math>) applies to ball milling when the ratio of reduction (<math>R_{\rm r}</math>) is low: | |||
:<math>{\rm EF7} = | |||
\begin{cases} | |||
\dfrac{2 \, (R_{\rm r} - 1.35) + 0.26}{2 \, (R_{\rm r} - 1.35)}, & \text{if ball milling and } R_{\rm r} < 6\\ | |||
1.0, & \text{otherwise}\\ | |||
\end{cases} | |||
</math> | |||
The '''rod milling factor''' (<math>{\rm EF8}</math>) accounts for rod milling inefficiencies: | |||
:<math> | |||
{\rm EF8} = | |||
\begin{cases} | |||
1.4, & \text{rod mill only, open-circuit crushing}\\ | |||
1.2, & \text{rod mill only, closed-circuit crushing}\\ | |||
1.2, & \text{rod–ball mill circuit, open-circuit crushing}\\ | |||
1.0, & \text{all other configurations} | |||
\end{cases} | |||
</math> | |||
== Excel == | == Excel == | ||
| Line 22: | Line 147: | ||
:<math>Parameters= | :<math>Parameters= | ||
\begin{bmatrix} | \begin{bmatrix} | ||
\ | {\rm WI}\text{ (kWh/t)}\\ | ||
F_{80}\text{ (}\rm{\mu}\text{m)}\\ | F_{80}\text{ (}\rm{\mu}\text{m)}\\ | ||
P_{80}\text{ (}\rm{\mu}\text{m)}\\ | P_{80}\text{ (}\rm{\mu}\text{m)}\\ | ||
| Line 38: | Line 163: | ||
\begin{bmatrix} | \begin{bmatrix} | ||
W\text{ (kWh/t)}\\ | W\text{ (kWh/t)}\\ | ||
\ | {\rm EF1}\\ | ||
\ | {\rm EF2}\\ | ||
\ | {\rm EF3}\\ | ||
\ | {\rm EF4}\\ | ||
\ | {\rm EF5}\\ | ||
\ | {\rm EF6}\\ | ||
\ | {\rm EF7}\\ | ||
\ | {\rm EF8}\\ | ||
\end{bmatrix}\;\;\;\;\;\;\;\;\;\;\;\; | \end{bmatrix}\;\;\;\;\;\;\;\;\;\;\;\; | ||
</math> | </math> | ||
where: | where: | ||
* <math>\ | * <math>{\rm WI}\text{ (kWh/t)}</math> is the Bond Work Index of the ore being processed (kWh/t) | ||
* <math>F_{80}\text{ (}\rm{\mu}\text{m)}</math> is the 80% fraction passing size of the feed (µm) | * <math>F_{80}\text{ (}\rm{\mu}\text{m)}</math> is the 80% fraction passing size of the feed (µm) | ||
* <math>P_{80}\text{ (}\rm{\mu}\text{m)}</math> is the 80% fraction passing size of the product (µm) | * <math>P_{80}\text{ (}\rm{\mu}\text{m)}</math> is the 80% fraction passing size of the product (µm) | ||
| Line 57: | Line 182: | ||
* <math>\text{Control fraction passing}</math> is the product size control reference fraction passing value (frac) | * <math>\text{Control fraction passing}</math> is the product size control reference fraction passing value (frac) | ||
* <math>D\text{ (m)}</math> is the mill diameter (m) | * <math>D\text{ (m)}</math> is the mill diameter (m) | ||
* <math>L\text{ (m)}</math> is the | * <math>L\text{ (m)}</math> is the rod length (m) | ||
* <math>\text{Rod mill}</math> indicates if the comminution device is a rod mill | * <math>\text{Rod mill}</math> indicates if the comminution device is a rod mill | ||
* <math>\text{Rod mill only circuit}</math> indicates if the circuit includes a rod mill only | * <math>\text{Rod mill only circuit}</math> indicates if the circuit includes a rod mill only | ||
* <math>\text{Closed circuit crushing}</math> indicates if the feed is prepared with closed circuit crushing | * <math>\text{Closed circuit crushing}</math> indicates if the feed is prepared with closed circuit crushing | ||
* <math>W</math> is the operating work index (kWh/t) | * <math>W</math> is the operating work index (kWh/t) | ||
* <math>\ | * <math>{\rm EF}1-{\rm EF}8</math> are efficiency factors applied to the calculation of operating work index. | ||
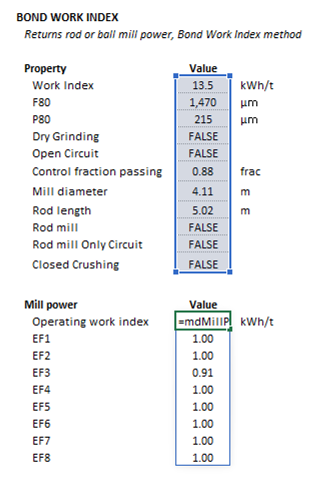
| [[File:BondWI1.png|left|frame|Figure 1. Example showing the selection of the '''Parameters''' (blue frame), and '''Results''' (light blue frame) arrays in Excel.]] | | [[File:BondWI1.png|left|frame|Figure 1. Example showing the selection of the '''Parameters''' (blue frame), and '''Results''' (light blue frame) arrays in Excel.]] | ||
Latest revision as of 14:53, 21 May 2025
Description
This article describes the Bond method for estimating the specific energy of rod and ball mill comminution circuits.[1]
Model theory
The Bond method estimates the specific energy required for comminution based on ore grindability and the extent of size reduction. It is derived from Bond's third theory of comminution, which states that energy consumption is proportional to the reduction in the square root of particle size. The Bond method applies to both rod mills and ball mills.
The specific energy consumption, (kWh/t), is given by the Bond equation:
where:
- is the Bond Rod Work Index or Bond Ball Work Index, depending on the application (kWh/t)
- is the 80% passing size of the feed (μm)
- is the 80% passing size of the product (μm)
To correct for variations from the standard test conditions (wet, closed-circuit grinding in a 2.44 m diameter mill), the model includes eight efficiency factors:
The correction factors are described below. A conversion factor of 1 tonne = 1.102 short tonnes is applied to work index terms.
The dry grinding factor () increases the specific energy required for dry grinding compared to wet grinding:
The open circuit ball mill factor () increases the specific energy required for open circuit grinding compared to closed circuit grinding. The factor accounts for the reduced efficiency when no classifier or closing screen is used to control the maximum product size.
The control size is the hypothetical closing screen size that would be used in an equivalent closed circuit. If the mill is in open circuit, is interpolated from the table below based on the percentage of the product passing the control size. For closed-circuit grinding (including all rod mill configurations), .
Table 1. Open-circuit inefficiency factors based on % passing control size (after Rowland, 2006).[1] % Passing Control Size Inefficiency Multiplier, EF2 50% 1.035 60% 1.050 70% 1.100 80% 1.200 90% 1.400 92% 1.460 95% 1.570 98% 1.700
The diameter efficiency factor () scales specific energy for mill diameter, (m):
The oversized feed factor () applies when the mill is to grind a feed that is coarser than an optimum 80% passing feed size, (μm):
where:
and:
The fineness of grind factor () applies when the is finer than 75 μm:
The high or low ratio of reduction rod milling factor () accounts for reduced efficiency when the reduction ratio in rod milling is too high or too low:
where:
and is rod length (m).
The low ratio of reduction ball milling factor () applies to ball milling when the ratio of reduction () is low:
The rod milling factor () accounts for rod milling inefficiencies:
Excel
The Bond specific energy model may be invoked from the Excel formula bar with the following function call:
=mdMillPower_BondWI(Parameters as Range)
Invoking the function with no arguments will print Help text associated with the model, including a link to this page.
The Parameters array and model results are defined below in matrix notation, along with an example image showing the selection of the same arrays in the Excel interface:
|
where:
|